基于多目标不确定性改进的GM-PHD滤波器
2023-01-05王奎武张秦虎小龙
王奎武, 张秦, 虎小龙
(1.空军工程大学 防空反导学院,陕西 西安 710051;2.空军工程大学 研究生院,陕西 西安 710051)
0 引言
多目标跟踪(MTT)问题是将量测值或标记分配给目标,并按时间步长来处理多个目标航迹的问题[1-2],对目标数量的准确估计,是提高多目标跟踪性能的前提。随机有限集(RFS)为解决多目标跟踪问题提供了统一的框架,将其与概率假设密度(PHD)滤波方法[3]相结合,在解决先验知识不足、目标数量未知等情况下的目标跟踪问题具有良好的潜力,目前广泛应用于雷达目标跟踪[4-6]、计算机视觉[7]、及时定位与地图构建[8]和群目标跟踪[9]的研究。
高斯混合(GM)和序贯蒙特卡洛(SMC)是PHD运算的两种重要方法,分别称为GM-PHD[10]和SMC-PHD[11]。其中,GM-PHD无需明确的数据关联[12-14],能够大大减少运算量,可有效避免PHD滤波过程中因数据关联产生的“组合大爆炸”问题。但对于目标间隔很近的情况,尤其是在杂波环境中,GM-PHD滤波器的估计性能下降显著。为此,Yazdian-Dehkordi等[15-16]通过改进高斯分量权重,改善了邻近间隔场景下的估计性能,但是这种方法存在连续漏检时错误率高、关键参数的调整缺乏明确依据等问题。为了提高目标数量估计的准确性,Vo等[17]提出GM-PHD滤波器的改进方案,可对目标数量的估计性能得到改善,但算法计算量大,存在估计延迟等问题。
为此,本文提出一种改进的GM-PHD滤波器。该方法从量测值来源衡量多目标的不确定性,区分量测是否是杂波、量测是否是同一个目标和没有量测三种情况。采用新的误差协方差更新方程体现目标量测值的不确定性,并进一步通过设计自适应阈值,按分量相似度进行合并以减少不相关分量的影响。所提出的算法保证了目标数量估计的准确性,进而提高了GM-PHD滤波的鲁棒性,同时具有计算消耗的优势。
1 GM-PHD滤波算法
1.1 PHD滤波器

(1)
v(xk|Zk)=[1-PD,k]v(xk|Zk-1)+
(2)
式中:ps,k|k-1为k-1时刻目标在k时刻的存活概率;f(xk|xk-1)表示状态转移概率密度函数;b(xk)和β(xk|xk-1)分别为新生和衍生RFS的目标强度[18];PD,k为k时刻目标的检测概率;gk(zk|xk)为单目标似然函数;λ为泊松杂波分布的密度;c(zk)为泊松杂波分布的概率密度函数。
1.2 GM-PHD滤波器
GM-PHD滤波器将多目标先验PHD和后验PHD(1)式、(2)式视为高斯分量,其可表示为类似于卡尔曼滤波器(KF)的递推更新结构。
假设k-1时刻多目标后验PHD可表示为GM形式:
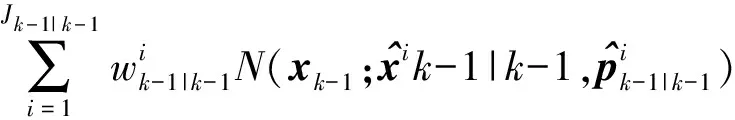
(3)

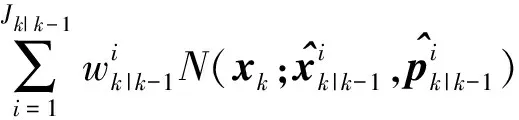
(4)
v(xk|Zk)=[1-PD,k]v(xk|Zk-1)+
(5)
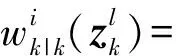
(6)
(7)
(8)
(9)

2 改进GM-PHD算法
2.1 估计误差协方差修正
在实际的目标跟踪过程中,估计误差的协方差与量测是真实目标、量测是杂波和无量测这3个事件有关。在杂波环境下,这3个事件可能随时发生。
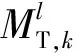
假设错误量测的数量m具有密度为λ的泊松分布[3]:
(10)
式中:VG为监视区域的大小。
可根据上述3个事件导出估计误差协方差,所提算法使用距离信息和所有量测值的排序来评估单个量测值来自目标的高斯分量的条件概率。

(11)
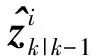
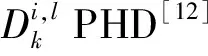
(12)

(13)
Cn为系数,由(14)式给出:
(14)
(15)

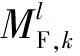
1) 情况1:未检测到目标;
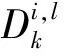
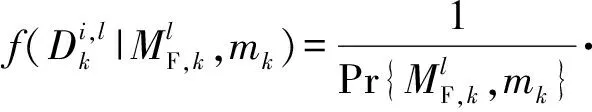
(16)

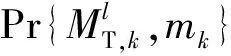
(17)
式中:
(18)
(19)
可以证明k时刻量测总数为mk的概率为

(1-PD)μF(mk)+PDμF(mk-1)
(20)
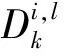
(21)

2.2 均方误差状态估计
计算每个高斯分量的状态估计的误差协方差。第i个高斯分量的先验和后验估计误差定义为
(22)

(23)
(24)
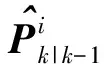
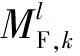
(25)
(26)
式中:
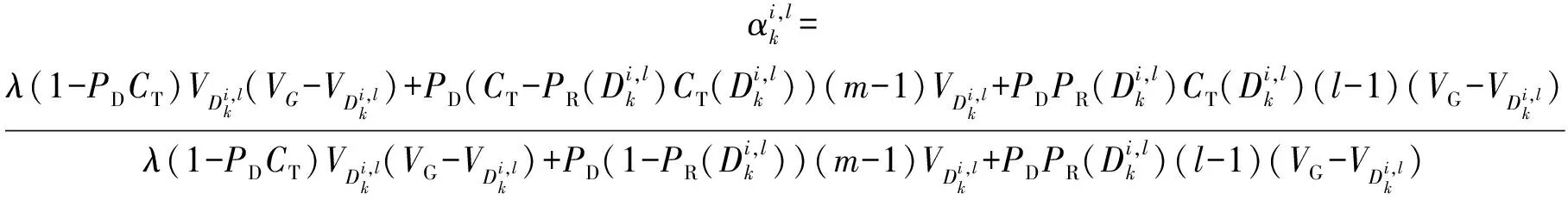
(27)
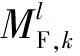

v(xk|Zk)=[1-PD,k(xk)]v(xk|Zk-1)+
(28)
式中:
(29)

(29)式考虑了来自杂波的量测的高斯分量的协方差。由于目标与杂波分量的差异,可以在下一时刻增加来自目标量测值的新生分量的权重,从而防止目标状态估计值的丢失。
2.3 高斯分量的合并方法改进

(30)
式中:Um为合并门限阈值,如果两个分量满足(30)式则合并为一项。由(30)式可以看出,常规合并只考虑了每个分量的均值和协方差,并没有考虑权重。在密集杂波环境下,当所跟踪的目标中有距离较近的目标时,会因为彼此距离太近而根据(30)式合并为一个新分量,而实际上,这些合并分量的权重大于预设的状态提取阈值。也就是说,这些合并的分量不应该被合并。因此,GM-PHD滤波器在跟踪距离较近的目标时,估计精度会显著恶化。
为此,在RFS框架下对合并方法作以下改进:
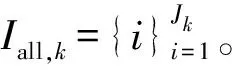
2) 设目标后验强度中权重最大分量的阶数为
(31)
3) 在k时刻与目标后验强度中最大权重分量具有最大相似度分量的阶数集合为
(32)
(33)
式中:σs为量测噪声值。
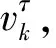
(34)
(35)
(5)式满足以上条件后,目标后验强度由(36)式表示:
(36)
从(33)式可以看出,Umm是一个自适应阈值,与第i个分量的权重以及量测噪声有关。Umm在合并过程中可以动态调整,它能够较好的适应目标紧密间隔的情况,从而改善传统GM-PHD固定阈值带来的估计误差。
3 仿真实验
3.1 试验参数设置
为了说明本文算法在模拟多目标跟踪场景中的有效性,将改进GM-PHD滤波器和GM-PHD滤波器以及高斯混合势概率假设密度(GM-CPHD)[21]滤波器进行比较,设置实验参数如下。
场景设置为多个目标在4个可能的位置出现或者从其他目标产生,观测区域为[-1 000 m,1 000 m]×[-1 000 m,1 000 m]。真实目标的数量为12,为简单起见,假定每个目标都做匀速直线运动,由于噪声和杂波的存在,目标量测值在不同时刻随机出现,因此数量会随时间变化,新生目标的强度由(37)式给出:
(37)

目标的状态向量由其位置和速度组成:xk=[px,kpy,kvx,kvy,k],其状态方程为
(38)
式中:T为采样间隔,T=1 s,总跟踪时间为100 s;wk为过程噪声,wk~N(0,5)。新生目标的过程噪声为高斯分布,均值为0,协方差为
(39)
式中:diag(·)表示对角矩阵。新生的目标的权重为0.03。量测向量表示目标的位置,zk=[pzx,kpzy,k],量测方程由(40)式给出:
(40)
式中:nk为量测噪声,nk~N(0,5)。在高斯分量剪枝部分,高斯分量的截断阈值设置为10-5,提取阈值设置为0.5。
设检测概率为0.98,幸存概率为0.99。Monte Carlo仿真次数为100。通过最优次模式分配(OSPA)评价估计精度:
OSPAp,c(xk,k)=
(41)
3.2 仿真结果
图1显示了模拟的真实多目标运动场景,其中多目标运动包括交叉以及邻近运动的情况。

图1 真实目标轨迹Fig.1 Real target trajectory
图2和图3显示了改进GM-PHD滤波器在杂波率分别为10和60的多目标跟踪场景,估计值不同颜色对应于不同的目标,错误量测在100 s内均匀生成。由图2可以看出,改进GM-PHD滤波器对于交叉运动以及邻近运动的目标跟踪效果较好,尤其是多目标运动分别在40 s和80 s时出现多个目标交叉运动,从滤波跟踪结果来看本文滤波算法较好地区分了各个目标,目标交叉运动后量测值没有出现混乱。

图2 低杂波环境(λ=10)改进GM-PHD 滤波器跟踪结果Fig.2 Improved GM-PHD filter tracking results in a low clutter environment (λ=10)

图3 密集杂波环境(λ=60)改进GM-PHD 滤波跟踪结果Fig.3 Improved GM-PHD filter tracking results in a dense clutter environment (λ=60)
图4和图5分别显示了在杂波率为10和60的两种情况,图6显示了检测概率设置为0.8时本文提出的滤波方法与GM-PHD滤波器、GM-CPHD滤波器的OSPA距离值比较。由图4可以看出:在杂波较低的情况下,改进GM-PHD滤波器拥有更好的滤波性能;当杂波增大或者检测概率降低时,可看到GM-PHD滤波器和GM-CPHD滤波器的滤波误差明显增大,尤其分别在40 s和80 s附近误差峰值会增高,原因是杂波环境中杂波的存在以及邻近目标难以区分导致误差耦合,而本文改进GM-PHD滤波器仍然保持了较好的滤波性能,可见,由于在高斯分量合并方面的改进,本文方法在杂波背景下,具有较好的滤波性能。

图4 OSPA距离(λ=10)Fig.4 OSPA distance (λ=10)

图5 OSPA距离(λ=60)Fig.5 OSPA distance (λ=60)

图6 低检测概率OSPA距离Fig.6 OSPA distance with low detection probability
为了进一步分析滤波算法性能差异,对各算法估计目标数量的性能进行比较。
图7和图8分别显示本文算法与GM-PHD滤波器、GM-CPHD滤波器在杂波率为10和60的情况下对目标数量的估计结果,图9显示了低检测概率条件下的情况。从图8和图9中可以看出,当目标趋近于交叉运动时,估计误差会急剧增大。在图9中可以看出传统GM-PHD滤波器在低检测概率条件下性能表现较差,当目标分别在40 s和80 s附近出现交叉运动后,跟踪性能下降较为严重。由图7、图8和图9可见,无论在杂波较弱还是在杂波较强的情况下,或者检测概率较低的情况下,改进GM-PHD滤波器都能够获得最好的目标数量估计性能。
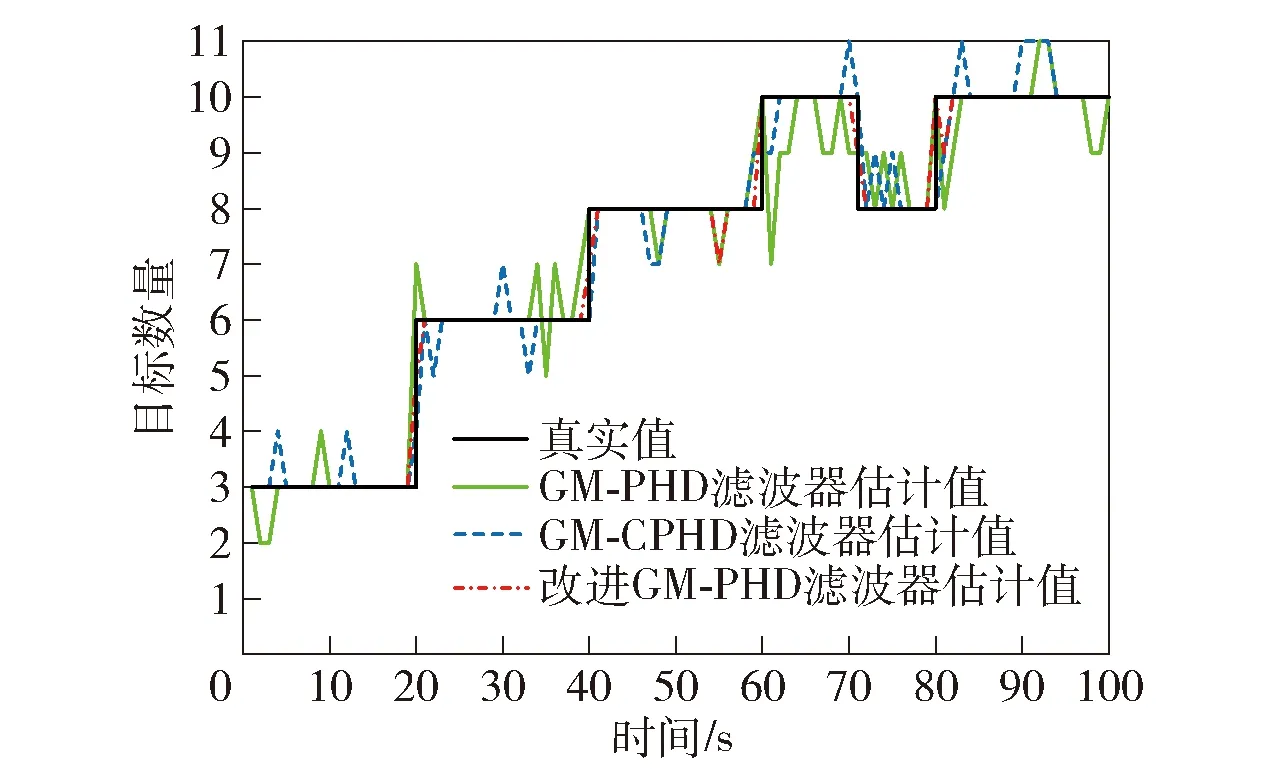
图7 低杂波环境(λ=10)目标数量估计Fig.7 Estimation of the number of targets in a low clutter environment (λ=10)

图8 密集杂波环境(λ=60)目标数量估计Fig.8 Estimation of the number of targets in a dense clutter environment (λ=60)
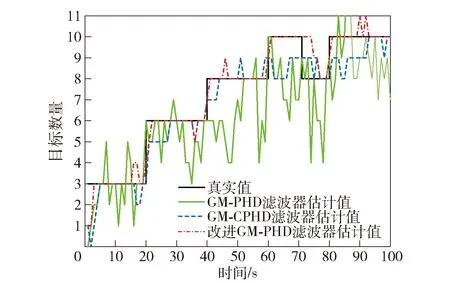
图9 低检测概率环境目标数量估计Fig.9 Estimation of the number of targets in an environment with low detection probability
通过对图7、图8目标数量估计结果的进一步分析可以发现,在目标跟踪初始阶段,由于协方差足够大,GM-PHD和改进的GM-PHD滤波器都能表现出较好的估计性能,这一过程可持续达20 s。但是,当目标出现或消失时,由于GM-PHD滤波器对误差协方差的更新没有考虑量测来自多目标的不确定性,从而使其估计性能显著下降,而改进GM-PHD滤波器始终保持了较好的估计性能,对目标数量的估计接近真实值。在60 s时,多目标会出现邻近交叉运动,从图8和图9可以看出,GM-PHD和GM-CPHD滤波器都出现目标数量的估计误差,但改进GM-PHD滤波器仍旧保持较好的跟踪性能,也证明了剪枝合并步骤改进的自适应阈值对邻近多目标跟踪性能的提升效果。

图10 不同杂波率环境下OSPA距离对比Fig.10 Comparison of OSPA distances under different clutter rates
图10和图11展示了不同杂波率的算法性能对比。从图10中可以看出,随着杂波率的不断提高,GM-PHD滤波器的跟踪误差成线性增长,其原因是随着杂波的不断增多,高斯分量剪枝合并步骤变得难以处理,导致各种误差出现误差耦合。而改进的GM-PHD滤波器利用修改过的估计误差协方差对量测源进行区分以及剪枝合并步骤的自适应阈值,有效避免了邻近目标以及杂波较多的问题。从图11中可以看出随着杂波率提升,GM-CPHD滤波器的计算量成线性增长,而改进的标签GM-PHD滤波器计算量变化幅度不大,这也体现了该算法的稳定性。
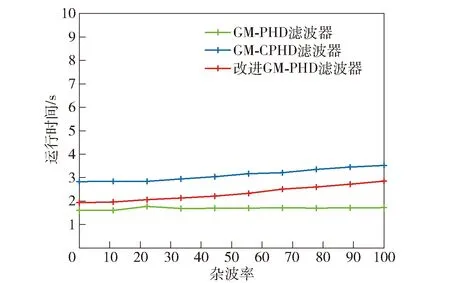
图11 不同杂波率环境下运行时间对比Fig.11 Comparison of running time under different clutter rates
图12和图13展示了不同检测概率条件下算法性能的对比。从图12中可以看出改进的标签GM-PHD滤波器相较其它算法稳定性更高,在不同检测概率条件下跟踪性能具有一定的优势。

图12 不同检测概率下OSPA距离对比Fig.12 Comparison of OSPA distances under different detection probabilities

图13 不同检测概率下运行时间对比Fig.13 Comparison of running time under different detection probabilities
4 结论
本文针对杂波场景下由于目标量测值出现的不确定性而导致目标数量估计误差的3种情况,对GM-PHD滤波方法进行改进,在考虑高斯分量的情况下,基于对条件误差的计算来更新协方差,使协方差通过权重反映了多目标的不确定性。在考虑权重的基础上进行高斯分量的合并,提高阈值的自适应性,保证滤波器对杂波环境下邻近目标的适应能力。
理论分析和仿真结果表明,本文方法对在杂波环境下,目标OSPA距离小,跟踪精度更高,同时,目标数量的估计结果受杂波的影响更小,其估计值更接近真实的目标数量。
