基于MLP-SVM的驾驶员换道行为预测
2023-01-05密俊霞于会龙席军强
密俊霞, 于会龙, 席军强
(北京理工大学 机械与车辆学院, 北京 100081)
0 引言
高级驾驶辅助系统(ADAS)利用车载设备采集行车数据,并对驾驶行为进行提前预测,可提醒驾驶员即将到来的危险场景,使驾驶更安全、高效。人类驾驶行为的不确定性,为ADAS的应用带来了挑战[1]。ADAS包括电子稳定控制系统(ESC)、车道偏离预警系统和换道辅助系统等。车道偏离预警系统在车辆不开转向灯却并入车道时,通过发送音频或者视觉警告给驾驶员以提醒。该系统通过摄像头检测车道线,来判断驾驶员是否产生了无意识的漂移。换道辅助系统通过使用传感器检测车辆周围环境并监控驾驶员的盲点,帮助驾驶员安全完成变道。当驾驶员打算换道时,如果有其他车辆从后面接近或着有其他车辆处于驾驶员盲区时,换道辅助系统将通过音频或视觉通知驾驶员。文献[2]研究结果表明,因换道引起的交通事故占机动车交通事故的9%。准确、提前预测出驾驶员的换道意图,可降低车道偏离系统的错误预警率,提升换道辅助系统的性能,对高级辅助驾驶系统的应用具有重要意义。
影响驾驶员换道意图预测准确率的两个主要因素是特征数据和算法。驾驶员意图预测的特征数据包括交通环境数据、车辆动力学数据和驾驶员行为数据。雷达、相机、GPS等可用于采集交通环境数据,包括道路信息数据,车辆距离道路中心线的距离,车辆的坐标,车辆相对于周围车辆的速度和位移等。车辆动力学数据可用CAN总线采集,包括车辆的速度、加速度、方向盘转角等。驾驶员行为数据主要包括眼动数据、头动数据、脚动数据、大脑活动数据等。驾驶员意图预测的算法包括隐马尔可夫模型(HMM)、贝叶斯网络(BN)、支持向量机(SVM)、高斯混合模型(GMM)、卷积神经网络(RNN)、长短时神经网络(LSTM)等。
国内外的学者在驾驶员换道行为预测方面展开了研究。其中HMM、SVM、GMM、BN及由这些模型组合成的混合模型被广泛应用于驾驶员意图预测。丁洁云等[3]采用对驾驶人换道决策有影响的环境参数,基于模糊逻辑理论设计了综合决策因子,来表达驾驶员做出换道决策的可能性,并且将综合决策因子与表征车辆横向运动的特征参数作为观测变量,采用HMM模型,识别驾驶员的换道意图。宗长富等[4]建立了双层HMM模型来辨识驾驶员所处的复合工况,其中上层多维离散HMM模型对应驾驶员所处于的复合工况,下层多维高斯HMM模型对应驾驶员在这段时间内的驾驶行为。宋晓琳等[5]提出了HMM-SVM的混合模型,用于驾驶员换道行为辨识,模型的输入特征为方向盘转角、油门踏板数据,将驾驶员的意图分为车道保持、紧急左换道、紧急右换道、正常左换道、正常右换道。刘志强等[6]运用HMM和SVM联合的算法,建立了驾驶员意图预测模型,确定6个参数的驾驶员意图预测指标,分别预测出车道保持意图、换道意图、超车意图。Butakov等[7]建立了两层模型来描述换道行为,其中底层为运动学模型、上层为随机模型,运动模型的部分采用正弦曲线换道模型,随机模型的部分采用GMM模型。Kasper等[8]采用贝叶斯网络来预测高速公路场景下的驾驶行为。Morris等[9]采用关联向量机(RVM)模型来预测换道意图,该模型是SVM模型的贝叶斯延伸。Li等[10]采用流形学习和SVM来识别驾驶员的换道行为,模型只采用相机数据。Kumar等[11]联合SVM和贝叶斯滤波,将SVM的概率输出作为贝叶斯滤波的输入,然后根据贝叶斯滤波的输出来预测驾驶员意图。模型使用的特征数据包括车辆相对于车道线的侧向位移、车辆相对于道路的方向盘转角及其导数,为利用历史特征数据,模型使用的特征向量为特征数据在一个时间窗内的数据,试验结果表明模型能在1.3 s之前预测出驾驶员换道行为。Schlechtriemen等[12]研究结果表明,预测驾驶员换道意图最有用的特征包括车辆侧向速度、车辆相对于前车的速度和车辆相对于车道中心线的侧向位移。Liu等[13]采用数据融合方法,利用相机信息和云数字孪生信息,来预测驾驶员换道行为。基于统计模型的方法在挖掘驾驶行为特征方面具有局限性。
由于算法、算力的提升,深度学习在图像处理、语音识别、翻译得到了广泛的应用,深度学习可用于预测驾驶员行为意图。季学武等[14]采用LSTM识别驾驶意图,得到驾驶意图分别为左换道、直线行驶、右换道的概率。宗长富等[15]结合HMM和ANN,建立了驾驶员意图辨识与行为预测模型,辨识出紧急转向、正常转向和直线行驶3种工况。王庆年等[16]基于Takagi-Sugeno模型的模糊神经网络,生成了模糊推理系统的推理规则,从而识别驾驶意图,并且将基于意图识别的结果应用于优化混合动力汽车的控制策略,提高混合动力汽车燃油经济性。Dang等[17]将换道意图的预测作为回归问题而不是分类问题,采用LSTM来预测当前时刻至车辆越过车道线之前的时间。Li等[18]采用RNN的方法,利用周围车辆的动态交互数据,来预测高速公路驾驶员换道行为。Ou等[19]采用RNN的方法,利用驾驶员观察行为和驾驶环境数据,来预测驾驶员换道行为。Khairdoos等[20]采用基于LSTM的方法,利用驾驶员注视数据、头部位置和车辆运动数据,来预测驾驶员换道行为。
眼部动作、面部动作、头部动作可被用于驾驶员意图预测。Lethaus等[21]研究发现眼睛的动作与驾驶行为相关。Doshi等[22]采用各种不同的特征来测试眼睛动作和头部动作哪种更能预测驾驶员换道行为,其得出的结论为头部动作比眼部动作在预测驾驶行为时更有效,头部动作联合车道数据和车辆数据能作为预测驾驶员换道意图的良好特征。Lethaus等[23]采用眼部数据来预测驾驶员换道行为,并且对比了ANN、BN和朴素贝叶斯3种不同的算法。张立军等[24]采集了直行、左换道、右换道的视频数据、驾驶员运动状态和方向盘转角信号数据,基于视线方向及头部姿态估计算法,提取驾驶员头部和面部特征,采用统计学方法获得了各特征与驾驶意图的关联性。Deng等[25]利用环境和眼动数据来预测驾驶员换道行为。眼部动作、面部动作、头部动作数据的采集需要驾驶员佩戴相应的装备或者需要采集驾驶员的面部隐私,可能会对驾驶员行为产生干扰。
驾驶风格对驾驶员的换道决策有影响。Yang等[26]采用k-means聚类算法与K近邻算法相结合,用于分类驾驶员的不同换道风格,将换道风格分为温和型、模糊型、激进型三类。Li等[27]提出一种混合的模型,联合BN与GMM,采用眼睛注视数据来标签驾驶数据,预测了不同场景下的不同驾驶风格驾驶员的换道行为。
由于不同的驾驶员会表现出个性化的驾驶行为,基于多名驾驶员的驾驶数据所建立的驾驶员换道行为预测模型不能完全适用于单个的驾驶员,而对于单个驾驶员,采集足够的驾驶数据来训练模型不是总能实现的。基于此,迁移学习的方法被用来建立单个目标驾驶员的个性化换道行为预测模型。 Lu等[28-29]采用不同的迁移学习算法,利用其他驾驶员的驾驶数据和少量的、不充足的目标驾驶员数据来建立目标驾驶员换道行为预测模型。Lu等[30]为了解决驾驶模拟器采集的驾驶数据与实车采集的驾驶数据之间存在差异的问题,采用迁移学习的算法将驾驶模拟器数据映射为实车采集数据。
关于以上研究,基于统计模型的方法不能完全充分挖掘驾驶行为数据的特征,而深度学习在提取数据特征方面具有优势。眼部动作数据和头部动作数据虽然有助于预测驾驶行为,但是在人类日常驾驶时,佩戴采集眼部动作和头部动作的装备,或者安装采集面部识别的摄像头,并不能被所有驾驶员充分接受。为进一步提高驾驶员换道行为预测模型的预测准确率和预测时间,本文基于MLP算法,联合SVM算法,提出了一种联合的MLP-SVM模型。采用车辆数据和交通环境数据,建立驾驶员换道意图预测模型。采用真实的公开交通数据集highD[31]来验证提出的模型,并与其他模型进行对比,验证所提出的模型在预测准确率和提前预测时间方面的优越性。本文所提出的框架如图1所示。

图1 基于MLP-SVM的混合模型结构Fig.1 Architecture of the hybrid MLP-SVM model
1 驾驶员换道行为预测模型的试验场景和特征向量
左车道一般为快车道,换道行为发生的其中一个原因为,在当前车道上,主车的前方车辆速度较慢,主车为了获取更快速度,需要换道到左车道。因此选取驾驶员左换道场景进行建模研究。
1.1 驾驶员换道行为预测模型的试验场景
驾驶员换道行为预测模型的试验场景如图2所示,目的是研究主车、代号为SV的换道行为,同时考虑周围4个车辆的信息,包括当前车道前车PV、当前车道后车FV、左前车LP、左后车LF的驾驶数据。

图2 换道场景示意图Fig.2 Diagram of a lane changing scenario
1.2 主车与周围车辆的数据信息
为建立驾驶员换道行为预测模型,主要采集主车信息和周围车辆信息。在时刻i,主车的数据信息可以表示为
(1)

主车与周围车辆的相对信息可以表示为
(2)
(3)
(4)
(5)
(6)
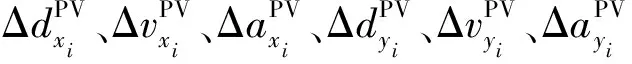
1.3 模型特征向量的选取与模型的输出
为建立驾驶员换道行为预测模型,主要采集主车信息和周围车辆信息。模型的输入是时刻i时,主车驾驶数据、周围车辆相对主车的驾驶数据和目标车道前车与后车的相对数据。
在时刻i,特征向量可表示为
(7)
模型的输出是时刻i+1时的驾驶员行为标签,可表示为
(8)
式中:0代表直驶行为;1代表换道行为。
2 基于MLP-SVM混合模型的驾驶员换道行为预测算法
多层感知机是深度学习的一种基本算法,可用于数据分类、回归。支持向量机常用于数据分类。本文为充分利用深度学习算法的特征提取能力,和支持向量机算法的分类能力,建立了多层感知机和支持向量机联合的驾驶员换道行为预测模型。
2.1 多层感知机算法
MLP模型包含一个输入层、至少一个隐藏层和一个输出层,图3为包含一个隐藏层,隐藏层有4个隐藏单元的多层感知机模型示意图。图3中,x1、x2、x3代表输入特征向量xi中的3个特征,h1、h2、h3、h4代表隐藏层中的4个隐藏单元,o1、o2代表输出层中的两个输出。

图3 多层感知机示意图Fig.3 Diagram of multilayer perceptron
包含K层的MLP模型含有一个输入层、K-1个隐藏层和一个输出层。MLP模型输出O的计算如(9)式所示:
O=H(K-1)W(K)+b(K)H(1)=φ1(XW(1)+b(1))
H(j)=φj(H(j-1)W(j)+b(j)),j=2,3,…,K-1
(9)
式中:H(k)、W(k)、b(k)、φk分别为第k层网络的输出、权重、偏差、激活函数,b(k)∈1×h(k),W(k)∈h(k-1)×h(k),h(k)为第k层网络的隐藏单元数;X为输入矩阵,X∈n×d,n为样本数,d为样本的特征数目。激活函数可以是ReLU函数或者sigmoid函数或者tanh函数等。给定元素x,各个激活函数的公式如(10)式~(12)式所示:
ReLU(x)=max (x,0)
(10)
(11)
(12)
本文建立的MLP模型包含三层:一个输入层,两个隐藏层,一个输出层。激活函数为ReLU函数,且由于换道行为的预测是一个分类问题,所以损失函数采用交叉熵损失函数,模型的权重和偏差通过后向传播算法计算。
(13)
式中:l(θ)为损失函数;θ为模型参数;q为类别数;ym和m为样本在m个类别上的真实标签和预测标签。
2.2 支持向量机算法
对于训练数据(xi,yi),xi∈d,yi∈{-1,1},SVM的目的是找到能把数据最大化分开的超平面ωTx+b=0,其中ω和b为超平面的法向量和截距,ω∈d,b∈。被分开的两类数据到该平面的距离的最小值相等,最优超平面为使此距离最小值最大化的超平面。xi到超平面的距离为缩放ω和b,使得|ωTxi+b|≥1,则离超平面最近的向量,即支持向量,到超平面的距离为1/‖ω‖,最大化1/‖ω‖等价于最小化基于SVM的分类问题可以定义为
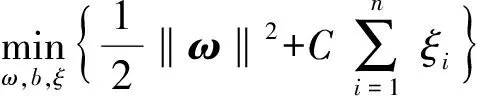
(14)
式中:ξi为非负松弛变量,当ξi=0时,为线性可分SVM;C为取值正数的惩罚参数,用于调和间隔尽量大与误分类尽量小。该问题是一个凸二次规划问题,其中ω有唯一解,b的解不唯一而是存在于一个区间。原问题的对偶问题为

(15)
式中:αi为拉格朗日乘子,可通过求解对偶问题的解再得到原问题的解。对于非线性分类问题,可以通过一个非线性变换,将非线性分类问题变换为线性分类问题,通过求解变换后的线性分类问题,得到原来的非线性分类问题的解。如果存在一个从输入空间中的xi变换到特征空间中的zi的映射φ(x),函数K(xi,xj)=φT(xi)φ(xj)总是成立,则称K(xi,xj)为核函数。核技巧应用于此的原因为:特征空间通常为高维,甚至为无穷维,显式地定义映射φ(x)通常是困难的,直接计算K(xi,xj)则比较容易。给定的核函数所对应的特征空间和映射的取法并不唯一。4种常用的核函数分别为线性核函数、多项式核函数、径向基核函数、sigmod核函数。表达式分别为
线性核函数:
(16)
多项式核函数:
(17)
径向基核函数:
(18)
Sigmoid核函数:
(19)
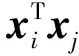
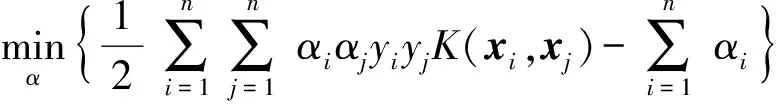
(20)
该问题可通过序列最小最优化(SMO)算法求解。SMO算法包含两个部分:采用启发式方法选择两个变量和采用解析方法求解两个变量的二次规划问题。在采用启发式方法选择两个变量时,不失一般性,假设选择的两个变量是α1和α2,其他的变量αi(i=3,4,…,n)固定。SMO在选择第2个变量α2时,需从训练样本中选择违反KKT条件最严重的样本点。此处的KKT条件可表示为
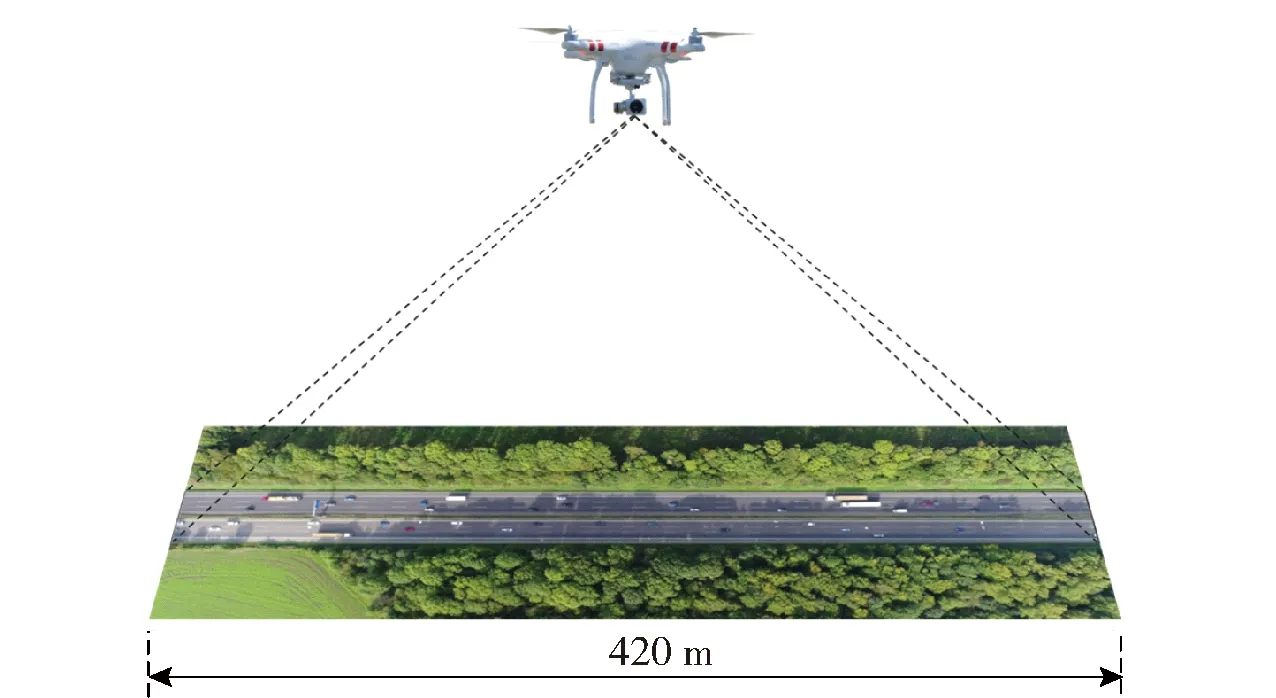
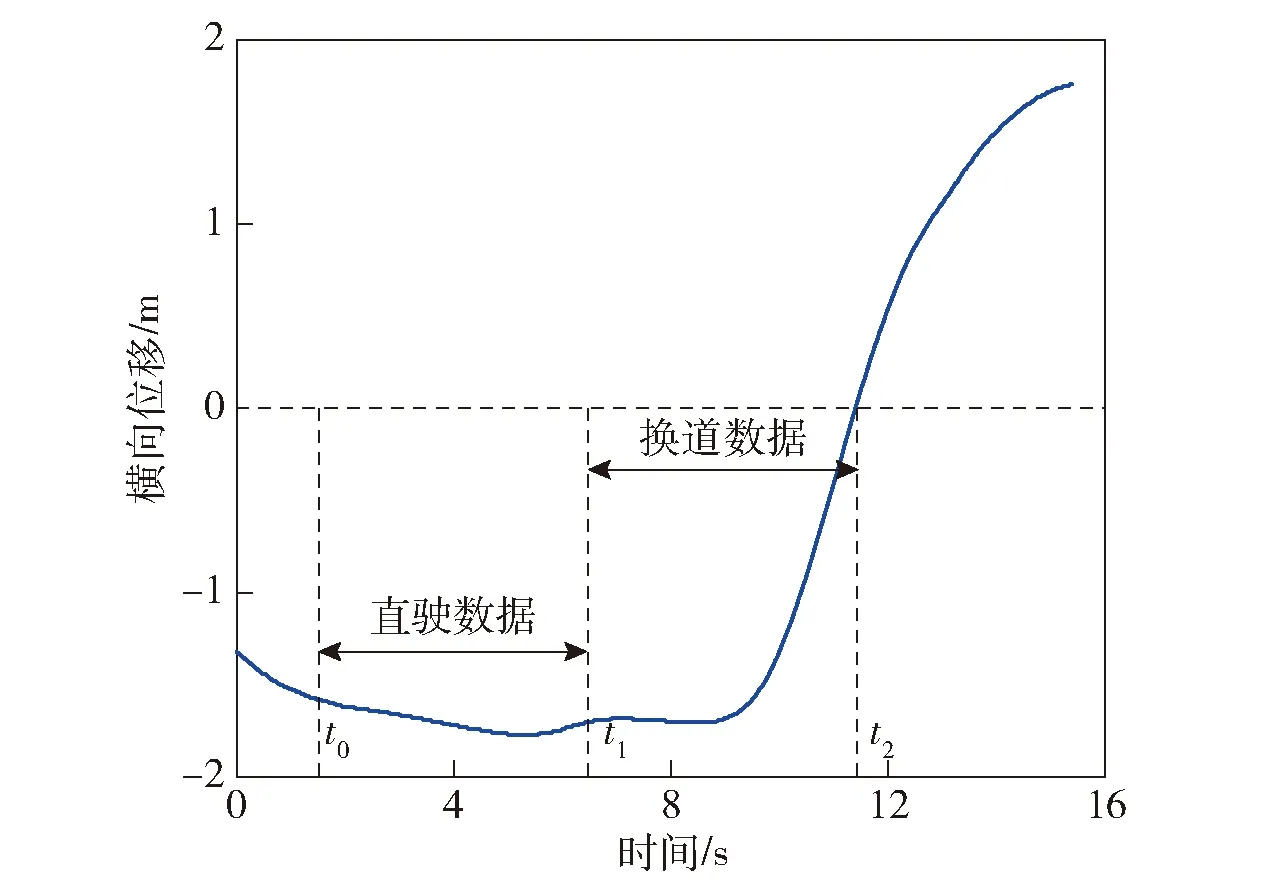
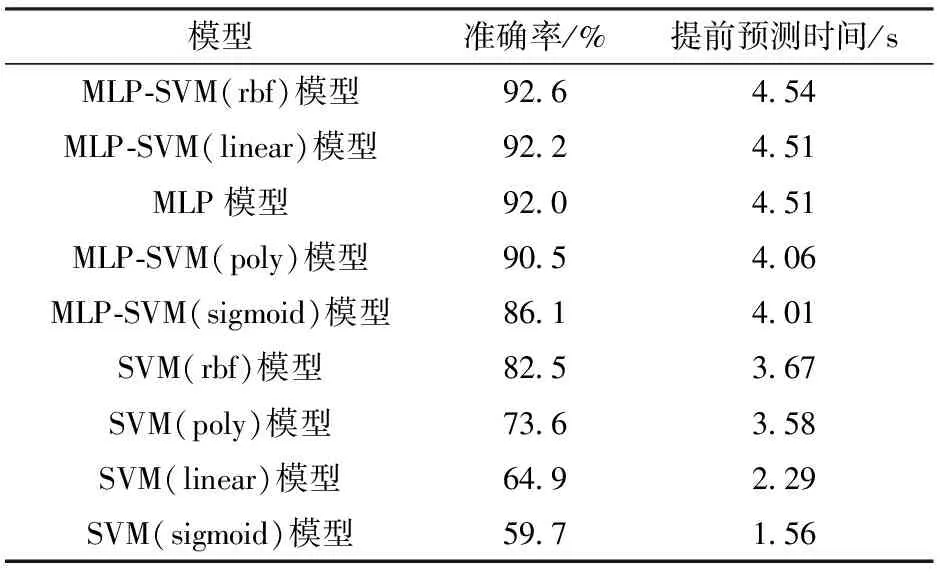
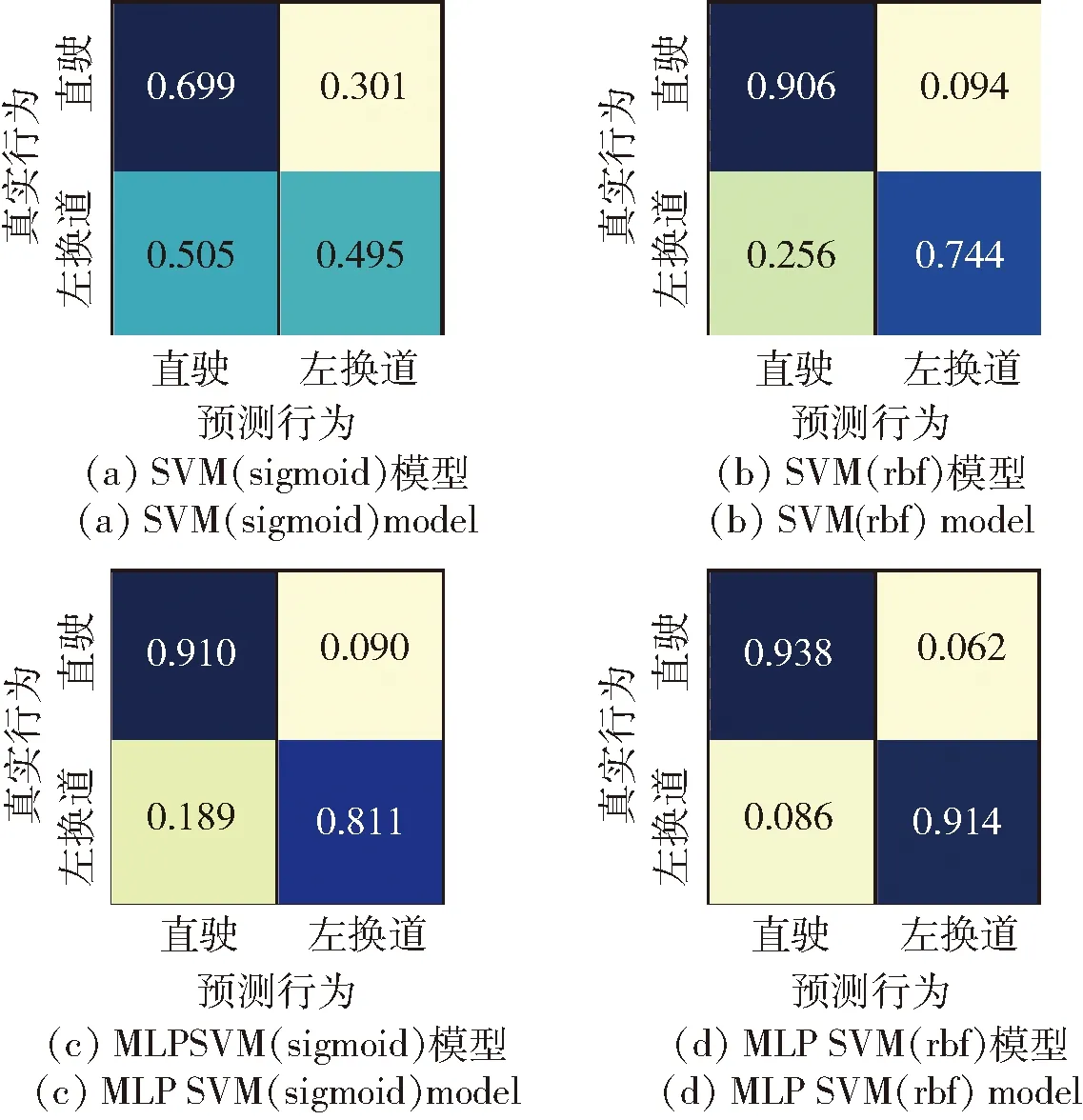
αi=0⟺yig(xi)≥1 0<αi (21) (22) α1和α2选择好后,SMO求解原问题对偶问题子问题可表达为 (23) (24) (25) (26) (27) 最终的分类函数为 (28) 图4 MLP-SVM混合模型结构与MLP模型结构Fig.4 Architecture sof hybrid MLP-SVM model and MLP model 本文所用的试验数据来自公开数据集highD[31],如图5所示,采用无人机航拍来获得驾驶数据。该数据集收集了德国高速公路上的约110 500个车辆的轨迹数据,数据采集的频率为25 Hz。 其中车辆包含汽车和卡车,本文采用汽车的数据来建立模型。主要研究自由换道,由于换道次数大于1有可能是强制换道,只选取换道次数为1的车辆。 图5 highD数据集Fig.5 HighD dataset 数据的处理方法如图6所示,采用时间窗的方式来标签换道行为,时间窗选择的时间为5 s。t2为车辆跨过车道线的时刻,t1为t2之前5 s的时间点,t1和t2之间时间的数据为换道数据,被标签为1,t0为t1之间5 s的时间点,t0和t1之间时间的数据为直驶数据,标签为0。 图6 数据处理方法Fig.6 The data processing method 数据处理后的训练数据和测试数据统计结果如表1所示。 表1 训练数据和测试数据统计Table 1 Summary of training dataset and test dataset 本文采用不同算法分别建立了驾驶员换道行为预测模型并且对比分析不同模型的性能。 所建立的换道行为预测模型,不仅要有整体的预测准确率,并且模型在换道时刻之前,越早预测出换道意图,则模型性能越好。因此,对于模型的评价,提出两个标准,即模型预测准确率、模型预测时间。 1)模型预测准确率。模型预测准确率的计算公式为 (29) 式中:TP为将正类预测为正类的数目;TN为将负类预测为负类的数目;FP为将负类预测为正类的数目;FN为将正类预测为负类的数目。 2)模型的精准度、召回率、F1分数分别为 (30) (31) (32) 3)模型提前预测时间。如果从换道之前的某个时间点至图6所示t2时刻,即车辆换道点,模型的所有预测结果均为标签1,即均为换道,则定义从这个时间点到车辆跨过车道线的换道点之间的时间为模型的提前预测时间。 车体是轨道交通车辆重要的承载结构,除必须满足强度、刚度、模态及结构稳定性等要求外,还必须满足日益提高的结构轻量化要求。碳纤维复合材料的应用为车体减重增能提供了新的思路,对推动轨道交通技术进步具有划时代意义。 MLP模型的参数如表2所示。 表2 MLP模型参数Table 2 Parameter selection and setting of MLP model 为验证所建立的MLP-SVM混合模型在驾驶员换道行为预测上的性能,分别基于MLP、SVM、MLP-SVM算法建立了驾驶员换道行为预测模型。为了选取合适的SVM模型,将SVM的核函数分别设为线性核函数、多项式核函数、径向基核函数、Sigmoid核函数。其中,SVM(sigmoid)、SVM(linear)、SVM(poly)、SVM(rbf)分别代表sigmoid核函数、线性核函数、多项式核函数、径向基核函数的SVM模型。MLP-SVM(sigmoid)、MLP-SVM(linear)、MLP-SVM(poly)、MLP-SVM(rbf)分别代表sigmoid核函数、线性核函数、多项式核函数、径向基核函数的MLP-SVM混合模型。 MLP在训练集上的损失随训练周期数的变化如图7所示,在10 000个训练周期后,训练集的损失趋于稳定,此时将MLP隐藏层的输出特征,作为SVM的输入特征,建立MLP-SVM模型。 图7 训练集损失随训练周期数的变化Fig.7 Training set loss changes with the number of training cycles 各个模型的预测准确率和平均提前预测时间对比如表3所示。以下为关于模型在预测准确率和提前预测时间方面的性能分析。 表3 模型的预测准确率和提前预测时间Table 3 Accuracy and advanced prediction time of the models 1)关于各个模型预测准确率的分析。由表3可知,对于SVM模型,不同的核函数对预测结果的影响很大,其中SVM(rbf)模型的预测准确率最高,为82.5%,SVM(sigmoid)模型的预测准确率最低,为59.7%。MLP模型的预测准确率为92.0%,在预测准确率方面优于SVM模型。对于MLP-SVM混合模型,SVM选取不同核函数对模型预测准确率也有影响,对于所设定的4种核函数,混合的MLP-SVM模型预测准确率均大于SVM模型预测准确率。当SVM的核函数选为径向基核函数时,在试验的所有模型中,混合的MLP-SVM(rbf)模型取得了最高的预测准确率,为92.6%。 2)关于不同的核函数在SVM模型和MLP-SVM模型中的不同表现分析。由表3可知,对于同一核函数,MLP-SVM模型的预测准确率均高于SVM模型。在SVM模型中,SVM(sigmoid)模型的预测准确率最低,在混合的MLP-SVM模型中,MLP-SVM(sigmoid)模型的预测准确率也最低。在SVM模型中,SVM(rbf)模型的预测准确率最高,在混合的MLP-SVM模型中,MLP-SVM(rbf)模型的预测准确率也最高。在SVM模型中,SVM(poly)模型的预测准确率高于SVM(linear) 模型,在混合的MLP-SVM模型中,MLP-SVM(poly)模型的预测准确率低于MLP-SVM(linear)模型。关于当核函数为rbf时,相对于其他核函数,SVM(rbf)和MLP-SVM(rbf)的预测正确率均为最优的解释为:rbf核函数将特征映射为无穷维,相比于其他核函数,获得了最优的分类结果,适合本文试验中特征维度不多、样本数量不过少也不过于多的状况。 3)关于模型的提前预测时间的性能分析。由表3可知,预测准确率越高的模型,更早预测出换道行为。对于不同核函数的MLP-SVM模型,MLP-SVM(rbf)模型的预测准确率最高,为92.6%,提前预测时间最长,为4.54 s。所选取的直驶换道时间窗为5 s,所建立的MLP-SVM(rbf)模型,在模型预测准确率和提前预测时间方面,均表现最优。而对于不同核函数的SVM模型,SVM(sigmoid)模型的预测准确率和提前预测时间分别为59.7%和1.56 s。由此可见所建立的MLP-SVM模型相对于SVM模型,在模型预测准确率和提前预测时间方面,都有较大的提升。 4)关于模型的混淆矩阵性能表现。为进一步对比所建立的混合MLP-SVM(rbf)模型和MLP-SVM(sigmoid)模型相对于SVM(rbf)模型、SVM(sigmoid)模型在预测性能方面的提升,图8分别显示了4个模型的正则化混淆矩阵。 图8 模型的正则化混淆矩阵Fig.8 Normalized confusion matrixes of models 从图8中可以看出,对于SVM(sigmoid)模型,在所有的真实换道行为中,只有49.5%的换道行为被预测出来,在所有的真实直驶行为中,只有69.9%的直驶行为被预测出来。SVM(rbf)模型与SVM(sigmoid)模型相比较,在预测直驶和换道行为方面的性能都有所提升,但是模型对两种行为的预测性能很不均衡。MLP-SVM(rbf)模型能分别预测出93.8%的直驶行为和91.4%的换道行为,在性能上与所建立的SVM模型对比有较大提升。 5)关于模型在精准度、召回率、F1分数方面的性能表现。表4为模型的精准度、召回率、F1分数。根据表4可知,相对于SVM模型,提出的混合的MLP-SVM(rbf)模型在精准度、召回率、F1分数方面的性能均有提升。 表4 模型的精准度、召回率、F1分数Table 4 Precision, recall, and F1 score of the models 6)关于模型在预测换道行为方面的具体显示。为进一步理解模型预测换道行为的能力,图9选取一条换道数据,分别显示车辆轨迹、真实的换道行为、MLP-SVM(rbf)模型、SVM(rbf)模型、SVM(sigmoid)模型对于该条换道数据的预测结果。 图9 预测结果的可视化Fig.9 Visualization of the prediction results 在图9中,MLP-SVM(rbf)的预测结果显示,该模型比真实换道标签延迟0.32 s预测出换道行为,而SVM(rbf)模型将3.16~5 s之间的直驶行为错误预测为换道行为,SVM(sigmoid)模型只有在5~7.12 s内的预测是正确的,其他的都为错误预测,显示了MLP-SVM(rbf)在换道行为预测方面优于SVM模型。 本文基于车辆运动数据及其周围车辆运动数据,建立了驾驶员换道意图预测模型,提出一种混合的MLP-SVM模型,通过MLP提取驾驶员的特征,采用SVM进行特征分类,预测驾驶员的换道意图,使用公开数据集highD进行了试验。得出以下主要结论: 1)基于MLP-SVM的模型在预测准确率方面高于基于SVM的模型。 2)SVM(rbf)模型的预测准确率为82.5%,提前3.67 s预测出换道行为。提出的基于 MLP-SVM(rbf)的驾驶员换道意图预测模型,充分利用了MLP模型提取数据特征的能力,和SVM的分类能力,取得了最高的预测准确率92.6%,可提前4.54 s预测出换道行为。本文提出的方法可应用于ADAS。

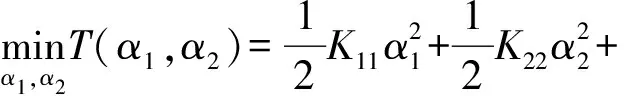
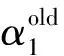


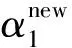
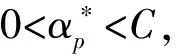
2.3 基于MLP-SVM的驾驶员换道行为预测模型

3 试验数据的处理

4 试验结果与分析
4.1 模型评价标准
4.2 模型设置

4.3 对比结果



5 结论
