超临界CO2在不同肋管中颗粒物沉积特性

毛 赏 周 涛 卢怀畅 刘文斌

(东南大学能源与环境学院，南京 210096)

超临界二氧化碳先进堆是目前国际上正在研究的新一代发电技术，有助于提高反应堆[1]的发电效率和热管堆的小型化[2]，也对实现碳中和有重要作用，在未来具有更大的发展潜力.但是核电厂各回路在运行中会产生细颗粒物杂质，在超临界CO2等反应堆中，颗粒物的存在会影响设备的使用寿命与安全性，还可能会产生破口事故，甚至引发重大事故，造成颗粒物和放射性元素释放到周围环境中，对生态环境造成不可逆的恶性影响.因此，为了保证核反应堆中设备的安全稳定运行，需要对颗粒物的运动沉积特性进行研究.已经有许多学者对颗粒物的沉积特性进行了研究，如吴建东等[3]通过实验研究了带有扰流挡板的管道内微细颗粒物沉积特性，结果表明管道中的挡板结构会对颗粒物沉积产生重要影响；朱亮宇等[4]对超临界水反应堆中的细颗粒物运动沉积进行研究，结果表明当管道长度较短或管径较大时，颗粒物的沉积不明显；Ma等[5]研究了不同颗粒物在超临界水中的运动沉积特性，发现不锈钢颗粒容易在入口处沉积而且沉积率随入口温度的增加而增加，而铝颗粒易在管道中部沉积并且沉积率随入口温度的增加而降低；此外，周涛等[6]对核电厂的事故以及颗粒运动特性进行分析，为事故条件下颗粒物运动沉积研究提供了理论基础.对于粗糙管道，也有一些学者进行了研究，如魏苗苗等[7]和Wang等[8]研究了带凸肋板和凹槽的通风管内的颗粒物沉积特性，发现布置凸肋板和凹槽更加有利于颗粒物的沉积；洪文鹏等[9]对粗糙壁流道内的颗粒物沉积特性进行研究，发现粗糙壁面可以提高颗粒物的沉积速度；黄秋焰等[10]对半圆形粗糙壁面的颗粒物沉积进行数值模拟，发现在肋的高度与直径比值e/d=0.02和肋距与肋高度的比值p/e=3时，颗粒物具有最大沉积速度.虽然已有相关文献对颗粒物沉积特性进行研究，但是其主要集中在空气中，对超临界CO2中颗粒物运动沉积的研究相对较少.此外，颗粒在不同肋管中的沉积特性尚未被发现.因此，本文通过数值模拟比较颗粒物在不同管道中的沉积特性并考虑超临界CO2物性参数对颗粒物沉积的影响，为超临界CO2中颗粒物的去除提供一定的参考，也有助于推动热管小堆的进一步发展.

1 研究对象

1.1 管道几何模型

考虑到工业中常用的管道通常为圆形，因此选用二维圆形管道作为研究对象.为了进一步研究不同管道类型对超临界CO2中颗粒物沉积的影响，建立了矩形肋管和半圆形肋管的几何模型，肋管和光滑管道具有相同的尺寸.建立的几何模型如图1所示.

从图1中可以看出，超临界CO2从左侧入口流入，从右侧出口流出，管道长度L=400 mm，直径d=20 mm.为了消除入口段的影响，在距离管道入口处x=200 mm位置均匀释放颗粒.g为重力加速度，方向垂直于流动方向，沿y轴反方向.肋的高度和肋与肋之间的距离(肋距)分别用e和p表示.

(a) 光滑管

1.2 计算条件

本文的计算范围包括超临界CO2的速度u为2～6 m/s，温度T为290～330 K，颗粒物直径dp为1～10 μm，肋的高度与直径的比值e/d=0.2和肋距与直径的比值p/d=1.详细的计算参数如表1所示.

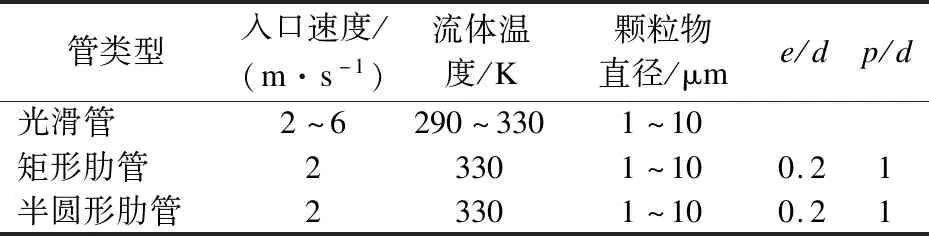
表1 几何模型计算参数

1.3 边界条件

采用Fluent软件进行数值计算，超临界CO2的压力场和速度场采用SIMPLE算法进行耦合.压力、动量和湍流动能采用二阶迎风格式(second order upwind)计算.入口和出口分别设置为速度入口(velocity inlet)和压力出口(pressure-outlet).管壁的边界设置为“wall”类型，管壁为无滑移边界条件.计算中认定颗粒物与壁面接触即为沉积，因此颗粒物在近壁面设置为“trap”，入口和出口设置为“escape”边界.模拟计算中，当所有的残差都小于10-5而且出口速度浮动值小于0.01 m/s时认为计算收敛.在x=200 mm处均匀释放20 000个颗粒，颗粒物的密度ρ=8 030 kg/m3.

2 计算模型

2.1 超临界CO2物性模型

超临界CO2的热物性参数随温度显著变化.在8 MPa下超临界CO2的物性参数[11]变化如图2所示.比热达到最大值时对应的温度为伪临界点温度Tpc.从图中可以看出，超临界CO2的热物理性质在伪临界点附近发生了巨大变化，这些都会影响颗粒物的沉积特性.对于超临界CO2急剧变化的物性参数，首先通过NIST软件计算超临界CO2物性参数，然后进行多项式分段拟合，最后通过用户自定义函数(UDF)编写代码，导入Fluent软件进行计算.

2.2 控制方程

流体在管内流动时，首先要判断流动状态，然后选用合适的方程进行求解.经过计算，超临界CO2在管内流动时，雷诺数大于2 300，因此判定流动模型为湍流.根据Wang等[12-13]的研究，AKNk-ε模型可以很好地预测超临界的流动换热特性，故本文采用如下AKNk-ε模型求解湍流模型：

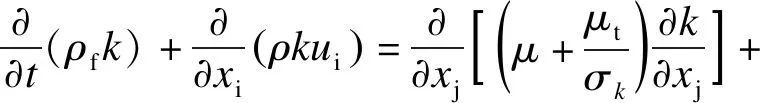
(1)

(2)

式中，ρf表示超临界CO2的密度，kg/m3；ui表示x方向的速度分量，m/s；k表示湍流动能，m2/s2；ε表示湍流耗散率；Gk为由速度梯度而产生的湍流动能，kg/(m2·s2)；Gb为由浮力而产生的湍流动能，kg/(m2·s2)；YM表示由于在可压缩湍流中过渡的扩散产生的波动；C1ε、C2ε、C3ε为常数；σk和σε为k方程和ε方程的湍流Prandtl数；μ和μt表示流体黏度和湍流黏度，Pa·s；Sk和Sε为用户自定义的源项，本研究中不涉及源项，取值为0.

在湍流k-epsilon模型中，湍流黏度和湍流动能、耗散之间的关系式如下.

(3)

式中，Cμ=0.09为常数.

2.3 颗粒沉积模型

2.3.1 颗粒受力模型

根据Ai等[14]的研究，流体中的颗粒受到布朗力、曳力和重力，颗粒物在流体中受到的力可由下式计算：

(4)

式中，mp为颗粒质量，kg；up为颗粒速度，m/s；FB为颗粒受到的布朗力，N；FD为曳力，N；FG表示颗粒受到的重力和浮力，N.

(5)

式中，ζ为正态分布随机数；S0为高斯随机函数；Δt为时间步长.

(6)

式中，Rep为颗粒的相对雷诺数；ρp为颗粒物密度，kg/m3；CD为曳力系数.Rep和CD可以由下式计算：

(7)

(8)

重力和浮力由下式计算：

(9)

式中，ρp和ρf分别为颗粒密度和流体密度，kg/m3.

2.3.2 颗粒沉积速度模型

颗粒的无量纲弛豫时间τ+可以由下式计算：

(10)

式中，S为颗粒密度与流体密度之比；ν为运动黏度，m2/s；u*为摩擦速度，m/s；Cc为坎宁安滑移修正系数.u*和Cc可以由下式计算：

(11)

(12)

式中，f为摩擦系数；τw为壁面切应力，Pa；l0为平均自由行程，对于超临界CO2气体平均分子自由行程l0=62.9 nm.

颗粒沉积速度和颗粒无量纲沉积速度[9-10]被广泛用于计算颗粒物在近壁面沉积的快慢，可以表示为

(13)

(14)

2.3.3 颗粒沉积效率模型

对于颗粒在管道中的沉积特性研究，沉积效率是评估颗粒沉积的一个重要参数. 颗粒物沉积效率可由下式计算：

(15)

3 网格无关性检验与模型验证

3.1 网格划分

为了精确地预测壁面附近流体的湍流特性，需要对壁面附近的网格进行加密处理，壁面附近的第一层网格的高度为0.01 mm，增长因子为1.2，设置10层边界层网格，壁面附近第一层网格的无量纲壁面距离y+≈1.不同管道的结构网格和局部放大网格如图3所示.

(a) 光滑管

3.2 网格无关性验证

考虑到计算成本和准确性等因素影响，分别设置网格的数量为2×104、3×104、4×104、6×104和8×104，用于验证网格无关性.以进出口的压降为研究对象，评估网格数量对计算准确性的影响，结果如图4所示.

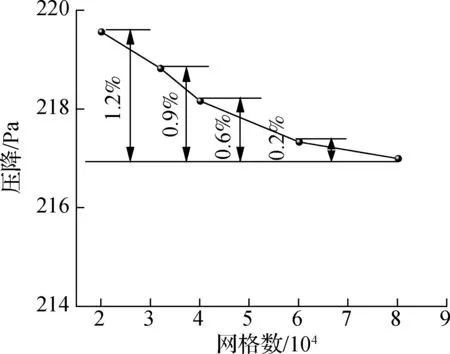
图4 网格无关性验证

从图4网格敏感性验证可以看出，当网格数量为2×104时，进出口的压降误差为1.2%；当网格数量从6×104增加至8×104时，管道进出口压降的误差仅为0.2%，表明在6×104以后增加网格数量对计算结果影响较小，因此综合考虑计算效率及准确性，选用6×104作为最终网格数量.

3.3 模型验证

为了验证模拟计算的准确性，选用无量纲沉积速度随无量纲弛豫时间的变化进行验证，并与Tian等[15]、Zhang等[16]、Liu等[17]、Wells等[18]的实验数据和Wood[19]、Fan等[20]的经验公式进行对比，结果如图5所示.从图5可以看出，所采用的湍流模型与实验值和经验公式具有相同的变化趋势，可以很好地复现颗粒物沉积速度随无量纲弛豫时间的变化.因此，所采用的湍流模型是可靠的.

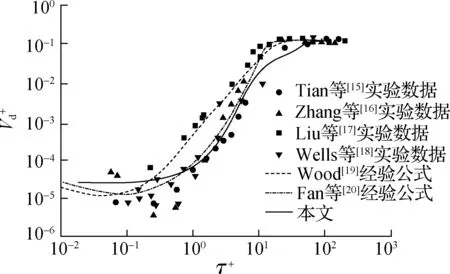
图5 无量纲沉积速度随无量纲弛豫时间的计算验证

4 计算结果及分析

4.1 流场分布

4.1.1 流速分布

在超临界CO2中，颗粒物的直径较小，容易受到流体速度场的影响，因此，对流场分析可以更好地揭示颗粒物的沉积机理.通过数值模拟计算，得到了不同管道内的速度场分布，如图6所示.

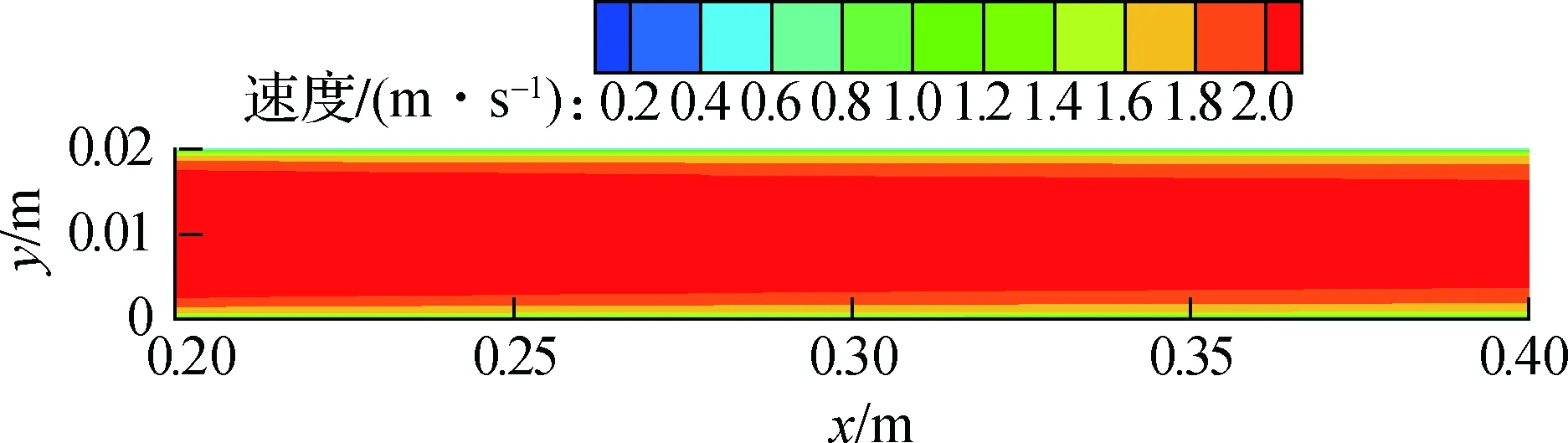
(a) 光滑管

由图6(a)可以看出，光滑管的边界层较薄，速度较小.如图6(b)和(c)所示，对于矩形肋管和半圆形肋管，由于肋的存在，使得超临界CO2的流道变窄，流体在经过第一个肋时流速增加，因此肋管流体的速度显著大于光滑管的速度.此外，从图6中还可以看出在相同的肋参数时，矩形肋管内的流体速度显著大于半圆形肋管内的速度.在第一个肋之后，半圆形肋管内的速度边界层变厚，然而矩形肋管内的边界层呈现波浪式变化.

4.1.2 湍流动能分布

管道内部的湍流动能也会影响颗粒物在壁面沉积，3种管道的湍流动能和流线分布如图7所示.从图中可以看出，肋管内的湍流动能显著高于光滑管的湍流动能.在e/d=0.2和p/d=1的条件下，肋管内的湍流动能是光滑管内湍流动能的10倍.大的湍流动能加速了颗粒与管壁的碰撞，从而提高了颗粒物的沉积效率.此外，矩形肋管与半圆形肋管相比具有较大的二次流区域.

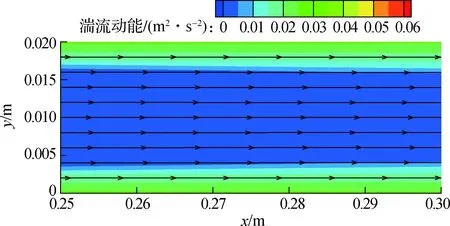
(a) 光滑管

4.2 流速对颗粒物沉积的影响

入口速度会影响管道内的流场分布，影响颗粒物的运动情况，最终影响颗粒物的沉积速度.对粒径为1～10 μm的颗粒、流速为2～6 m/s光滑圆管内颗粒物的沉积效率进行分析，计算结果如图8所示.由图8可以看出，当颗粒直径dp<5 μm时，颗粒沉积效率呈现出稳定趋势，几乎不随流速的变化而变化；然而当颗粒直径dp≥5 μm时，颗粒物的沉积效率随着流速的增加而减小.这是因为颗粒直径较小时，颗粒物主要受到布朗力和湍流耗散的作用，流速增加，增加了流体的湍流动能，加速颗粒沉积；但是随着流速增加，颗粒在管内的运动时间减小，因此颗粒物沉积效率呈现稳定趋势.随着颗粒直径的增加，颗粒物沉积主要受惯性力和重力的影响，流速的增加减小了颗粒物在管内的停留时间，颗粒物跟随流体一起流出管道，因此颗粒沉积效率随着流速的增加而减小.

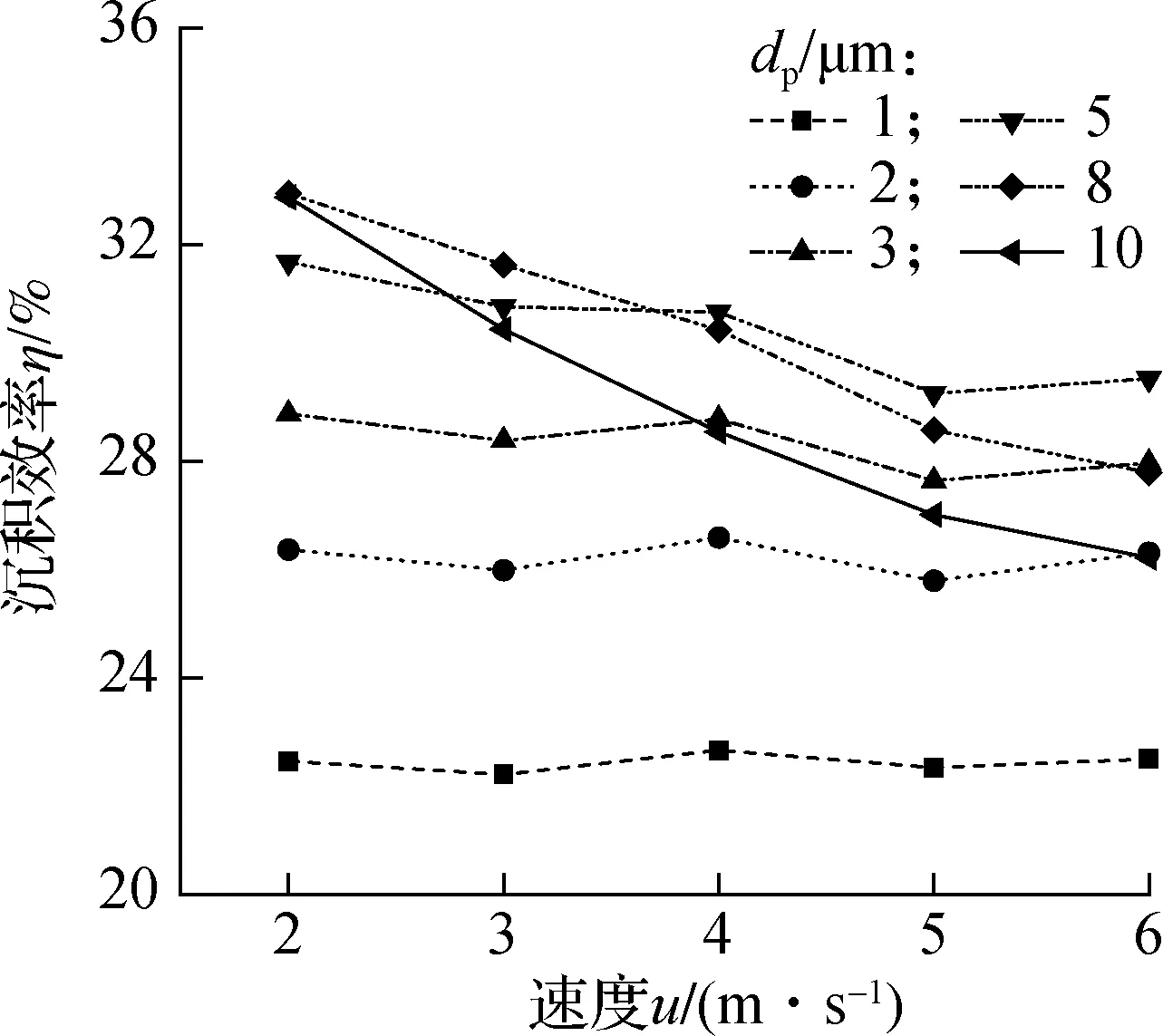
图8 颗粒物沉积效率随速度的变化关系

4.3 温度对颗粒物沉积的影响

超临界CO2的热物性质随着温度的变化而变化，不同温度条件下超临界CO2的热物性也会影响颗粒物的沉积特性.在光滑圆管中，颗粒物在不同温度条件下的沉积速度如图9所示.从图9中可以看出，超临界CO2温度在伪临界点(Tpc=308 K)以下时，随着流体温度T从290 K增加到300 K，颗粒沉积速度保持不变；当流体温度在临界点以上，从310 K增加到330 K时，颗粒的沉积速度显著增加.主要原因是随着温度的增加，超临界CO2从类似液态的流体转变为类似气态的流体，密度和黏度都随着温度的增加而降低，这些都有利于颗粒物的沉积.当超临界CO2温度在伪临界点(Tpc=308 K)以下时，超临界CO2是一种类似液态的高密度高黏度的流体，特殊的物理性质决定了超临界CO2中颗粒物沉积速度较小.因此在类液态区域，颗粒物沉积速度几乎不随温度的增加而增加.

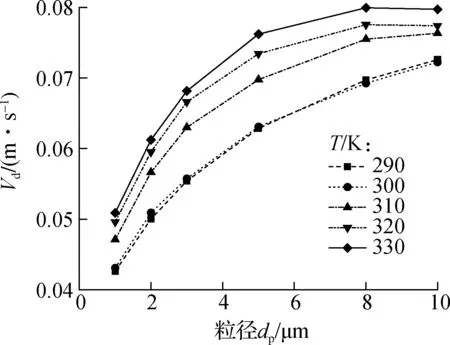
图9 颗粒物沉积速度随温度的变化关系

4.4 管道对颗粒物沉积的影响

为了比较不同管道内颗粒物的沉积特性，计算了光滑管道和加肋管道内颗粒物沉积速度随无量纲弛豫时间的变化以及沉积效率随粒径的变化，如图10所示.从图中可以看出，加肋通道内的颗粒物沉积速度和沉积效率显著高于光滑管道，这表明管道内加肋有利于颗粒物沉积.在e/d=0.2和p/d=1时，矩形肋管和半圆形肋管平均沉积效率比光滑管提高32%和28%.此外，矩形肋管的沉积速度和沉积效率大于半圆形肋管，这也表明颗粒在矩形肋管中更容易沉积.主要原因是矩形肋管在壁面附近具有更大的湍流动能(见图7)，这有利于颗粒物与壁面碰撞，沉积在壁面.

为了对比颗粒在不同管道内的运动轨迹，绘制了颗粒的轨迹图.不同管道内颗粒轨迹流线如图11所示.从图中可以看出，在光滑管道内，颗粒轨迹与管道平行，颗粒在管内均匀分布.对于矩形肋管和半圆形肋管，由于受到肋的扰动，颗粒的轨迹流线图更加无序，颗粒容易与壁面和肋碰撞.因此，在管内布置肋可以加速颗粒沉积.此外，从图11中可以看出，颗粒在矩形肋管中和壁面具有更大的碰撞概率，这也表明在矩形肋管中颗粒更易于沉积.

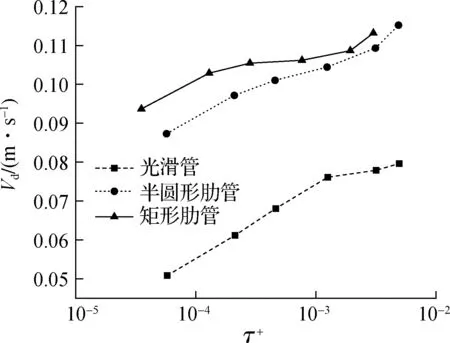
(a) 沉积速度随无量纲弛豫时间的变化

(a) 光滑管

5 结论

1) 增加流速可以增加流体的湍流动能.对于dp<5 μm的颗粒，增加流速对颗粒物的沉积效率几乎没有影响；对于dp≥5 μm的颗粒，增加流速可以降低颗粒物的沉积效率.

2) 当流体温度位于伪临界点(Tpc=308 K)以下时，温度从290 K增加到300 K，颗粒物的沉积速度保持不变.当温度超过伪临界点，从310 K增加到330 K时，沉积速度显著增加.因此，超临界CO2的温度保持在伪临界点以上有利于颗粒物沉积.

3) 在管内布置肋可以强化流体的湍流动能，加速颗粒物在管道内的沉积.在e/d=0.2和p/d=1时，矩形肋管和半圆形肋管平均沉积效率比光滑管提高32%和28%.