大规模小水电接入配电网三相线损异常检测方法研究
2023-01-05杨军亭李亚昕董晓阳
常 鸿 杨军亭 梁 琛 李亚昕 董晓阳
(国网甘肃省电力公司电力科学研究院)
0 引言
电力系统建设过程中,由于“重发轻供”理念,导致配电网三相线损长期居高不下[1]。而在供电系统运行过程中,线损率是电力规划和改造的主要依据。为了提升配电网运行稳定性,研究人员提出多种监测方法,实现线损计算与异常分析。但是在新能源接入配电网后[2],三相线损异常检测难度大幅提升,常规的异常检测方法,无法得出准确的判断结果。
国内有不少学者对线损异常检测进行分析,如徐迪等[3]应用k-means算法对原始检测数据进行聚类分析,明确电力系统当前负载状态。并应用孤立森林算法计算异常分数,得出线损异常检测结果。但是,该方法检测结果误差较大。张国芳等[4]依托于自编码器,对日线损率数据进行异常检测。其中,变分自编码器主要负责对线损率时间序列进行编码,并获取不同时间点的重建概率,当该概率值高于阈值时,表明此时存在线损异常情况。但是,该方法异常检测耗时较长。林宝德等[5]将原始配电网线损数据样本变换为二维数据,再从数据中提取特征向量。运用Hasusdorff距离公式计算不同多维特征属性的相似程度。最终,引入层次聚类算法,进行线损异常识别。但是,该方法检测结果召回率较低。
为解决以上方法存在的问题,提出一种大规模小水电接入配电网三相线损异常检测新方法。该监测方法主要包括四个环节,分别是特征提取、线损计算、聚类分析以及异常检测。通过算例分析可知,所提方法的异常检测结果极为准确,可以指导后续配电网规划与建设。
1 设计大规模小水电接入配电网三相线损异常检测方法
1.1 获取配电网三相线损特征量
为了更好地测量配电网三相线损特征量变化情况,文中借鉴均方根电流法,在配电网的各个支路上安装智能计量终端,采集各相电压和电流值,在此基础上进行线损特征测量提取[6]。计算过程中,先将采集数据转化为代数形式:

式中,b表示配电网支路;n表示相量;l表示测量时间;p表示实部;q表示虚部;η表示相电流;φ表示相电流相位;cos表示余弦值;sin表示正弦值。通过式(1)完成数据转换后,线损相关的电流特征量可以描述为:


1.2 计算小水电接入后三相线损
大规模小水电接入,会引起配电网运行模式的直接改变,使得线路损耗从最初的单一损耗,变为多支路线路损耗,大规模小水电接入前后配电网运行模式如图1所示。
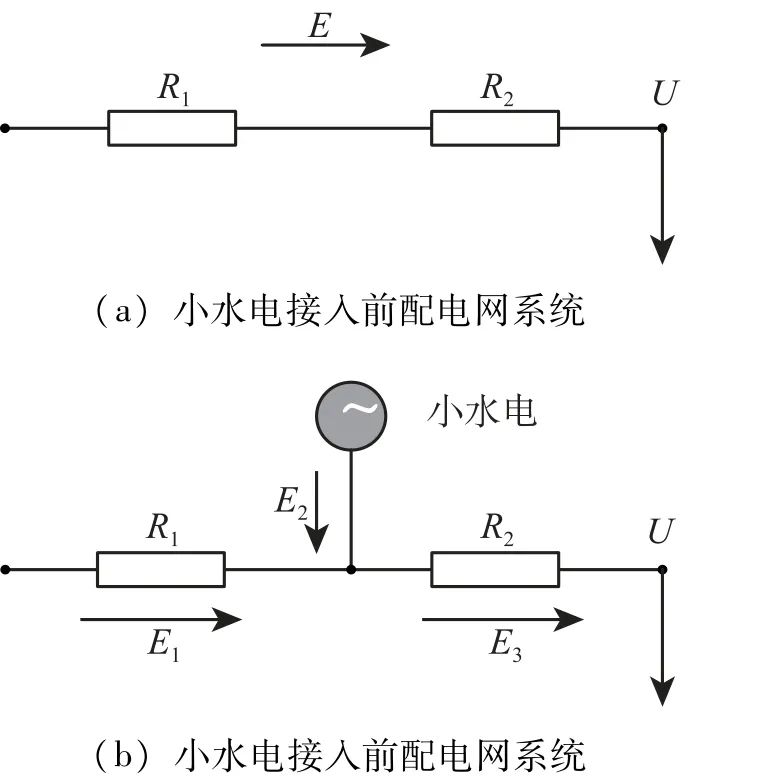
图1 大规模小水电接入前后配电网
图1中,R1、R2表示线路电阻,U表示额定电压,E表示线路损耗,E1、E2、E3表示小水电接入后支路线路损耗。
在小水电接入之前,可以直接将馈线首端设置为配电网的主变二次侧出口,再通过分段求解的形式获取等值电阻。而当小水电接入后,配电网结构发生改变,若馈线首端依旧处于不可选择状态,线损计算结果与实际情况出现偏差。为此,文中针对原始的等值电阻法进行改进,形成可随意选择馈线首端的改进等值电阻法[7],计算大规模小水电接入后三相线损数据。以接入两个小水电的馈线为例,根据馈线上正常供电量数据,可以得出等效供电量:

式中,I0表示馈线首端网平均电流;I1、I2表示小水电的供电电流;I3表示倒送电流;D0表示馈线首端网供电量;D1、D2表示接入的小水电站供电量;D3表示倒送电量;L表示馈线上配变器数量;c表示抄表电量;表示接入的小水电站等效供电量;表示等效倒送电量。
针对式(5)、式(6)、式(7)进行求解,得出等效供电量计算结果。按照上文提出的等值电阻法改进思想,建立如下改进等值电阻求解公式:

式中,R表示电阻值;表示导线的等值电阻;R'表示变压器绕组的等值电阻;N表示配电网线路分段数量;j表示分段;λ表示导线等效供电量;L表示配电网内配电变压器数量;k表示配电变压器;g表示配变等效供电量。
1.3 设计线损数据聚类分析方法
针对大规模小水电接入配电网三相线损数据,文中应用KNN算法进行聚类分析[8],完成线损数据的初步分类,将数据特征相似的数据汇总在一起。应用KNN算法进行数据分析时,对每一个数据样本提取负载率、用电比例等多项特征向量,形成如下所示数据特征向量集合:

式中,e表示线损数据;v表示数据的特征向量;r表示特征空间维度总数量;V表示数据特征集。
在式(10)的基础上,引入标准的欧氏距离计算原理,计算线损数据样本之间的距离:
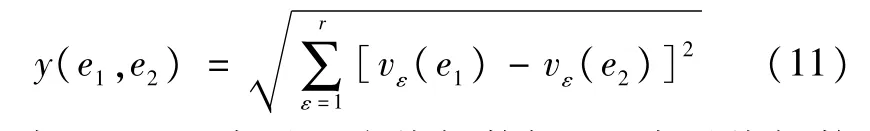
式中,e1、e2表示两个线损数据;y表示线损数据之间的欧式距离;ε表示某个特征空间维度;vε表示ε维空间内特征向量。
利用式(11),对三相线损数据集内的所有数据样本进行欧氏距离计算[9],再按照降序排列的方式,对数据样本进行合理排列。针对排序靠后且欧式距离最短的样本,将其划分为一类,且该类线损数据具有相似的特征。
1.4 生成三相线损异常检测结果
引入孤立森林计算理念,建立一个随机超平面,作为线损数据划分的主要工具[10]。直到保留唯一一个数据节点,就可以得到孤立树,数据空间分割模式如图2所示。
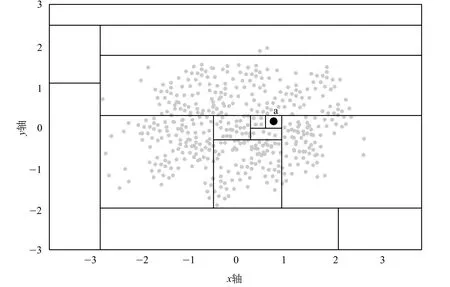
图2 数据空间分割示意图
按照图2所示的数据空间分割模式进行处理,最终得到数据点a。进一步计算孤立树的根节点、叶子节点之间的距离,识别该数据点是否处于离群状态。之后,按照同样的离群点判断方法对数据集内所有数据点进行分析,形成包含数棵孤立树的孤立森林。运用二叉搜索树和孤立树算法,进行配电网三相线损异常分数的计算:
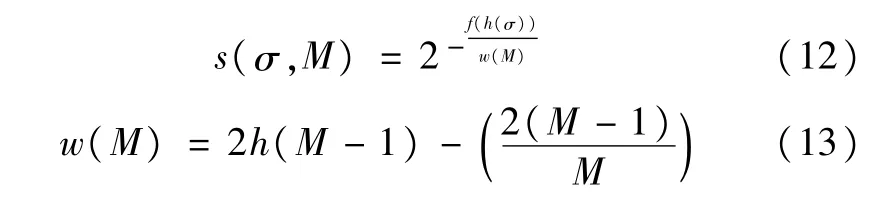
式中,σ表示节点;M表示数据点数量;s表示异常分数;h表示节点真实高度;f表示节点期望高度;w表示平均搜索长度。
通常情况下,配电网三相线损异常分数计算结果,呈现出单调递减函数特点,且异常分数计算结果越接近1,表明该数据点属于离群点的概率越高。对比预先设定的异常判断阈值和异常分数计算结果,当异常分数较高时,表明配电网的三相线损存在异常。
2 算例分析
2.1 算例结构
针对文中提出的线损异常检测方法,展开算例分析,体现该方法的优越性。本次算例分析选用IEE69节点配电网拓扑结构,搭建实验环境。同时,为了满足实验要求,在IEE69节点配电网内接入10个小水电,模拟大规模小水电接入环境,形成如图3所示的配电网拓扑结构。

图3 接入小水电站后的IEE69节点配电网拓扑图
为了便于后续分析,针对图3中的10个接入小水电站进行调查,得出其有功出力和无功出力情况如表1所示。

表1 小水电站接入节点、有功出力和无功出力
在上述实验环境下,应用文中提出的方法进行配电网三相线损异常检测。根据异常检测结果,验证本文研究内容的可行性。
2.2 三相线损异常检测结果
由于本文提出的三相线损异常检测方法,主要针对大规模小水电接入配电网环境。因此,在算例分析过程中,针对接入小水电的10个节点的线损率数据进行分析,生成三相线损异常检测结果。以接入节点28为例,小水电接入后,配电网三相线损率数据变化情况如图4所示。
按照文中研究内容,采用KNN算法对图4所示的三相线损数据进行聚类分析,得到如图5所示的聚类分析结果。

图4 节点28三相线损率数据
从图5所示的线损率聚类分析结果可知,节点28的平均线损率高于3.5%,且3个聚类中心之间的距离大于5%,表明线损数据样本中存在异常数据。再针对1类标签的聚类数据进行时间离散度分析,计算得出该节点的线损异常分数为0.55,需要进行线损异常警报。
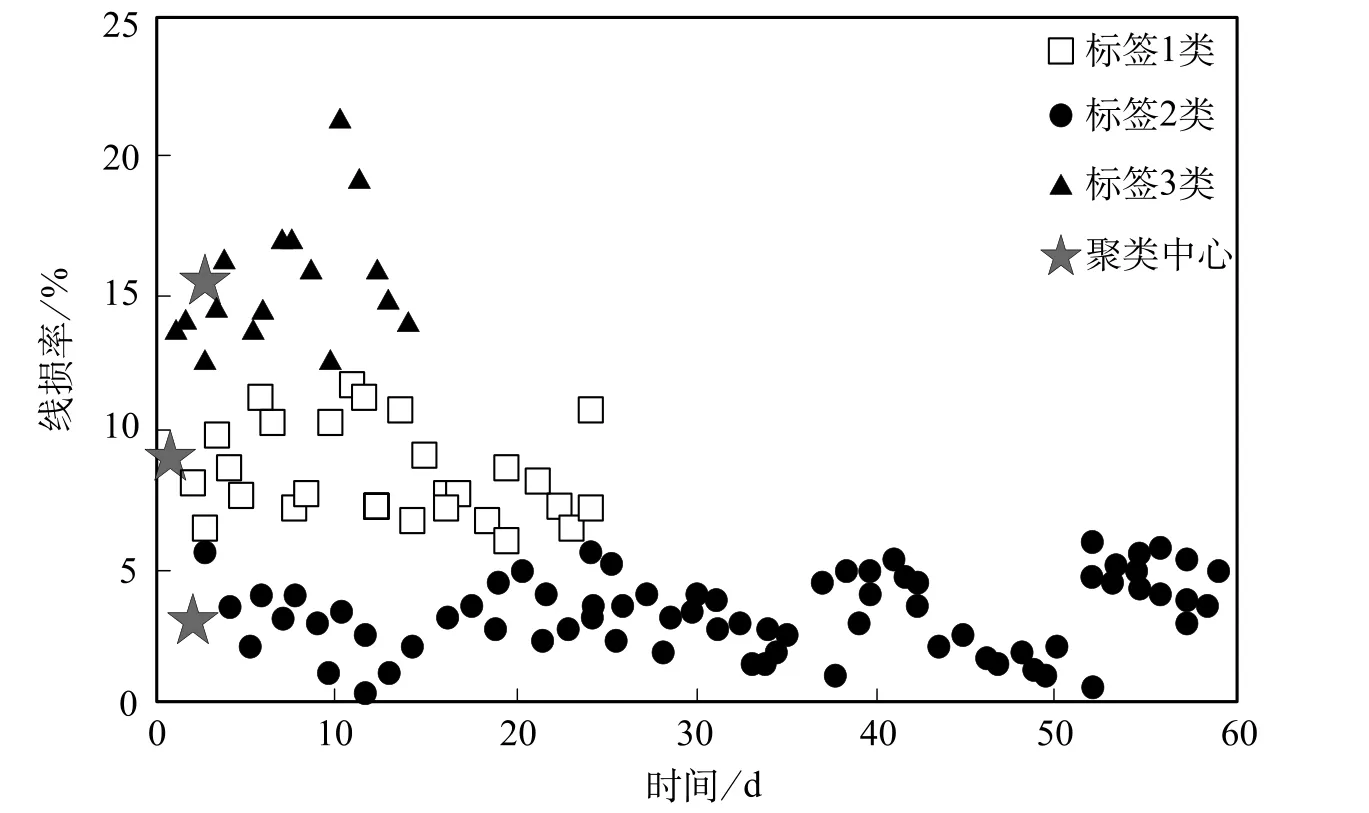
图5 节点28线损率聚类分析结果
按照同样的计算方式,对其余9个小水电接入节点,进行三相线损异常检测,得到如表2所示的异常检测统计表。
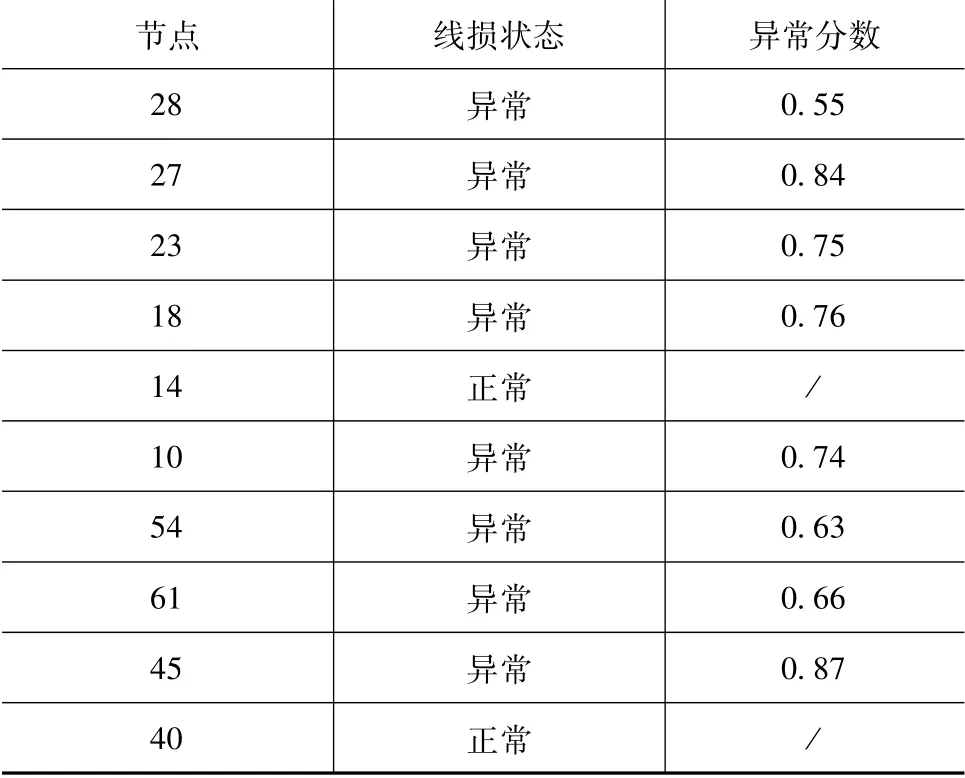
表2 配电网三相线损异常检测统计表
根据表2可知,10个小水电接入节点中,只有节点14和节点40的线损处于正常状态,其余8个接入节点的线损均为异常状态,且异常分数较高。从三相线损异常检测结果来看,文中所提方法具有实际意义,可以实现线损异常判断。
2.3 检测方法性能对比
此外,本次实例分析过程中,还选择基于变分自编码器的检测方法、基于多维特征的检测方法,同步针对小水电接入节点,进行三相线损异常检测,根据异常检测结果,计算不同检测方法的F1值:

式中,F1表示综合评价指标;α表示异常检测结果的精确率;β表示异常检测结果的召回率。基于式(14)对不同方法的线损异常检测结果进行计算,形成如图6所示的F1值对比结果。
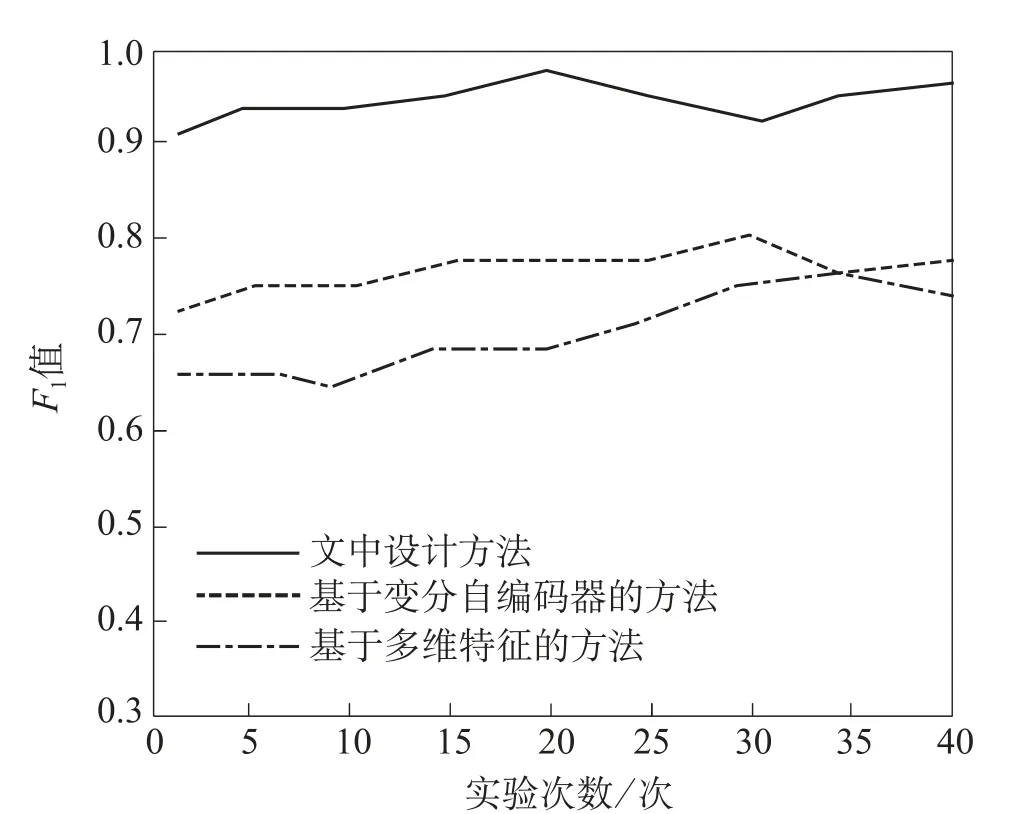
图6 不同线损异常检测方法的F 1值对比
根据图6可知,文中设计的线损异常检测方法的F1值保持在0.9以上,平均F1值为0.95。而其他两种检测方法的F1值分别为0.76、0.71。综上所述,采用本文设计的方法进行配电网线损异常检测,有利于检测结果的准确度提升,具体表现为F1值提升19%、24%。
3 结束语
面对大规模小水电接入配电网的情况,文中设计一种新的方法,针对复杂的三相线损进行异常状态检测。文中考虑到小水电接入会引起配电网运行模式更加复杂,在三相线损计算过程中,运用改进等值电阻计算公式,得到符合实际情况的线损数据,再进行后续聚类分析和异常检测,得到准确的检测结果。从算例分析结果来看,所提方法得出的三相线损异常检测结果更准确,在后续配电网建设过程中可以发挥指导作用。
