基于探地雷达和深度学习的果树根径预测方法

李光辉 王哲旭 徐 汇 刘 敏

(江南大学人工智能与计算机学院，无锡 214122)

0 引言

果树根系的粗细和深度能反映出果树的生长和健康状况，也影响着水果的产量与品质。根系在植物个体中扮演着至关重要的角色，它可以为植物提供生长所需的水和营养物质，同时还有支撑、固定植物体的作用，但根系相较于果树的枝干或冠层更加难以观察和取样，导致根系研究落后于植物的地上部分。当前的根系检测方法基本分为两类，破坏性检测和无损检测(Non-destructive testing, NDT)[1]。传统的破坏性检测可以精确获得根系直径信息，但费时耗力且可能对根系造成不可逆的破坏，在果树和古树名木的根系检测中不可取。探地雷达(Ground penetrating radar, GPR)作为一种新兴的无损检测技术，具有定位准确、速度快、使用灵活和探测精度高等特点，相对于其他无损检测方法(例如X射线断层扫描、核磁共振方法、声学方法和电阻率层析成像等)有着操作简单、携带便捷、可重复测量等优点，因此被广泛应用于探测浅层地下的未知物体[2-6]。探地雷达在树木根系和树干检测中也发挥着重要的作用，探地雷达检测根系的物理基础是根系与周围土壤含水率差异，即根系含水率明显高于周围土壤，使得两者的相对介电常数有着较大差异[7-15]。目前利用探地雷达进行植物根系探测研究主要集中在根系形态绘图、根生物量估计和根的定位等方面，使用探地雷达定量地预测树根半径仍然是一个难题[16-19]。

崔喜红等[20]通过实验建立了一个基于探地雷达波形信号的根径和根生物量的估测模型，在根径大于0.005 m的情况下，R2达到0.85。近些年，深度学习和探地雷达技术开始密切结合，2019年，GIANNAKIS等[21]提出了一种基于深度学习的探地雷达快速正向求解器。王泽鹏等[22]提出了一种基于YOLOv3的树根自动识别和参数估计的方法。对根双曲线的识别准确率和召回率分别达到96.62%和86.94%，根系参数预测的总平均相对误差在10.57%以内。目前，大多数基于探地雷达的深度学习方法都是用探地雷达二维数据(B-Scan)作为基础开展研究[23-27]，B-Scan数据是由实数组成的二维数组，与数字图像相似。因此这类方法能发挥深度学习在图像目标识别和分类方面的性能优势，但对于根系半径和深度来说，预测精度相对较低。对于根系半径的预测大多数使用数学方法，需要人工成本，且鲁棒性较低[28-31]。

为了解决以上问题，本文以探地雷达检测根系的一维数据(A-Scan)为研究对象，提出一种基于探地雷达和卷积神经网络的树木根系半径和深度的预测方法。使用注意力机制和卷积神经网络实现对树根半径和深度的预测，利用不同半径和不同深度的埋根实验获得的实测数据对本文方法的预测性能和鲁棒性进行评估与分析。

1 研究方法

1.1 注意力机制

注意力机制由MNIH等[32]首次提出并应用在图像分类领域，之后在机器学习领域快速发展。注意力机制源于人类视觉系统的处理机制，人类在处理视觉信息时会自动过滤掉不重要的信息，选择性去关注重点的目标区域，极大地提高了视觉信息处理效率和准确性。而注意力机制应用在基于神经网络的回归模型上还比较少，其本质是对输入数据的特征信息重新分配权重，为重要特征分配更大的权重，突出关键特征对模型的影响，以此大大提高模型收敛速度，用较小的计算资源换取模型性能的显著提升。

注意力机制主要有3个阶段，第1阶段计算出输入数据和标签数据的特征相似度，激活函数(Activation)设置为sigmoid，将A-Scan数据和标签导入多层神经网络(Multi-layer perceptron, MLP)进行计算。特征相似度计算公式为

simi(inputsi,labels)=MLP(inputsi,labels)

(1)

式中 simi——特征相似度函数

inputsi——输入数据

labels——标签值

MLP(·)——MLP网络

第2阶段根据第1阶段计算出的特征相似度进行数值转换。通过引入Softmax进行计算，一方面可以完成归一化操作，将原来的特征相似度整理成所有元素权重之和为1的概率分布，另一方面，可以通过Softmax的内在机制突出重要元素的权重。特征权重系数αi计算方法为

(2)

第3阶段把第2阶段得到的特征权重系数乘到输入数据中，获得重新分配权重的输入数据。对特征权重系数进行加权求和即可得到Attention数值。计算方法为

xnewi=αixi

(3)

(4)

式中xi——原始输入数据

xnewi——分配权重的输入数据

1.2 树根直径和深度预测模型设计

本文提出的预测方案是由2个预测模型组成，一个用于预测根系半径(AC-Net-R)，另一个用于预测根系深度(AC-Net-D)。它们是基于注意力机制和卷积神经网络的深度学习模型，以数值化的A-Scan数据作为输入，首先，通过注意力模块突出重要特征信息；然后，使用卷积层来提取特征信息，池化层可以减小网络结构的参数并保持特征不变，提高模型泛化能力；最后，通过全连接层将前面卷积层所学到的局部特征综合为A-Scan数据的全局特征。至此，所构建的模型可以自动学习获取根系半径或深度的主要特征，完成对根系半径或深度的预测。根径预测模型和深度预测模型如图1所示，图中Attention表示注意力模块；Conv1D，n表示卷积核尺寸；MaxPooling1D,/3表示步长为3的最大池化层；Dense,m中的m表示全连接层节点数量；Output为输出预测值。激活函数可以使神经网络逼近任何非线性函数，增强模型学习能力。因此，深度神经网络中激活函数的选择对模型性能有着重要影响。在本模型中，卷积层激活函数都是ReLU，全连接层激活函数都是PReLU，PReLU可解决模型梯度消失和梯度爆炸的问题，最后一层激活函数是linear，用于连续值预测。

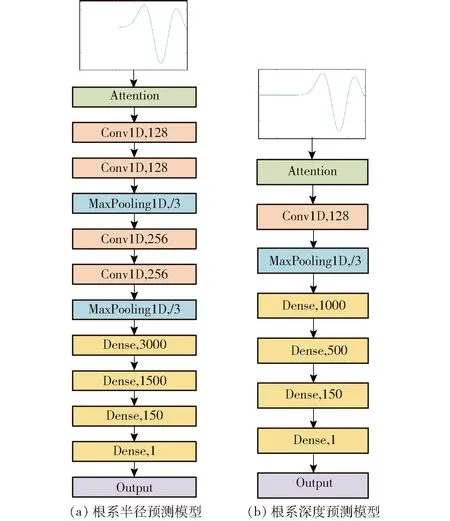
图1 预测模型

注意力模块(Attention)结构如图2所示，图中αi(i=1,2,…,3 000)为特征权重系数，“⊙”为逐个元素相乘，数值化的A-Scan数据通过2个由3 000个节点组成的全连接层计算得到特征权重系数，将权重系数与数值化A-Scan数据逐个元素相乘得到重新分配权重的A-Scan数据，以达到突出关键特征的目的。

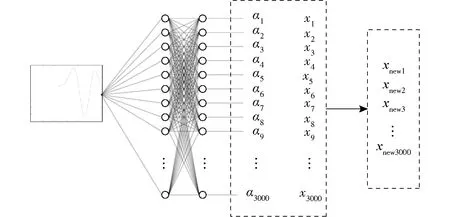
图2 注意力模块结构图

1.3 整体流程

本文方法流程如图3所示，共分为10步：使用gprMax生成仿真数据集完成模型的调参和训练，然后用真实的数据测试模型的可靠性和鲁棒性，在导入模型之前需要先将原始的B-Scan图像数值转换成矩阵，再通过去除直达波和标准化操作完成对原始数据的预处理，然后提取出双曲线顶点的A-Scan数据，最后导入训练好的模型进行预测得到预测结果。

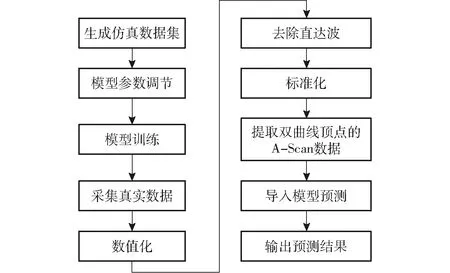
图3 方法流程图

1.4 结果评价指标

本文利用绝对误差、均方根误差、最大误差[28]和决定系数[20]来评价模型在仿真数据和实测数据上的预测效果。绝对误差是指预测值与真实值之差的绝对值；均方根误差可以评价模型预测的稳定性；最大误差是指一组数据中最大的绝对误差；决定系数常用于评价回归模型的拟合程度，决定系数越接近于1表示拟合程度越好。

2 实验结果与分析

2.1 数据集构建

一个标签良好、均匀分布的训练集在训练过程中至关重要，在很大程度上影响深度学习模型的整体性能[33]。为了预测树根半径，从真实数据中获取数据集耗时费力，需要人工埋根数千次，同时需要保证根的半径和深度的不同。为了克服这个困难，采用仿真数据集，可以保证标签的准确和数据集的数量。

仿真数据使用基于时域有限差分(Finite difference time domain, FDTD)方法求解麦克斯韦方程的开源软件gprMax生成[34]，仿真数据的参数设置如表1所示，设置沙土的介电常数为3～6 F/m的随机数，根系的相对介电常数为15～21 F/m的随机数，根的半径为5～30 mm的随机数，深度为 0～300 mm 的随机数。仿真数据中使用的天线是由地球物理探测公司(GSSI)制造的400 MHz商用GPR天线。图4表示生成一条A-Scan数据所需的空间模型纵向切面图，其中GSSI 400MHz天线放置在地面，位于被测根系的正上方。测得的单个A-Scan作为数据集中的一条数据，而不需要一个完整的 B-Scan数据，这样可以减少生成仿真数据所需的计算需求。树根被建模为圆柱形，同时与探地雷达天线保持平行。探地雷达天线与树根之间的介质设置为沙土，沙土与干土相对介电常数相差不大(干土相对介电常数为3 F/m)，且在实地埋根实验时不容易结块产生空气缝隙，以此来充分模拟实际根系在地下紧贴土壤生长的情况。训练集由3 100条A-Scan数据组成，每条数据有3 000个特征。训练集分为3部分，65%的数据用于训练，15%的数据用于验证，20%的数据用于测试。本文所有的训练和验证都是在半径5～30 mm和深度0～300 mm范围内进行。

表1 参数设置

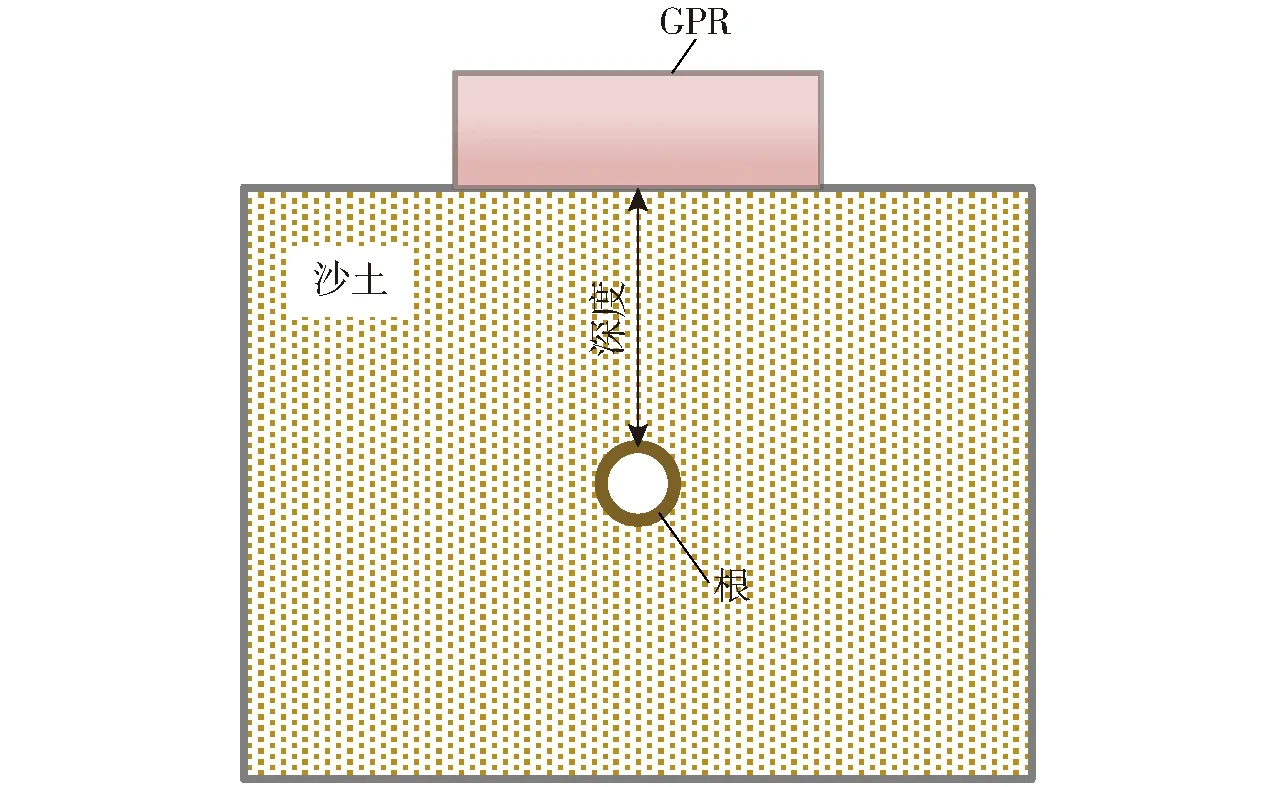
图4 生成一条A-Scan所需的模型

2.2 模型训练

实验运行环境为Intel Core(TM)i9-9900X @ 3.50 GHz处理器,内存64 GB，Nvidia RTX2080Ti显卡，12 GB显存。开发环境为Matlab 2020a、Python 3.6。模型的损失函数使用均方误差并采用Adam最小化实际值与预测值之间的均方误差，其中有偏一阶矩估计的指数衰减因子为0.9，有偏二阶矩估计的指数衰减因子为0.999，2个预测模型的学习率为0.000 3。模型迭代2 000次，每批次样本数量为64。在训练过程中，记录每次迭代损失值和决定系数，如图5、6所示，半径预测的模型训练损失值和验证损失值在第150次迭代附近下降迅速，在1 000次迭代之后，损失值趋于稳定。R2在第100次迭代附近快速上升，在750次迭代之后，R2曲线逐渐逼近1。深度预测模型的损失值和R2曲线在第1 500次迭代之前有明显的振荡，但在之后逐渐趋于稳定，曲线的其他走势特点与半径预测模型相近，所以不再赘述。

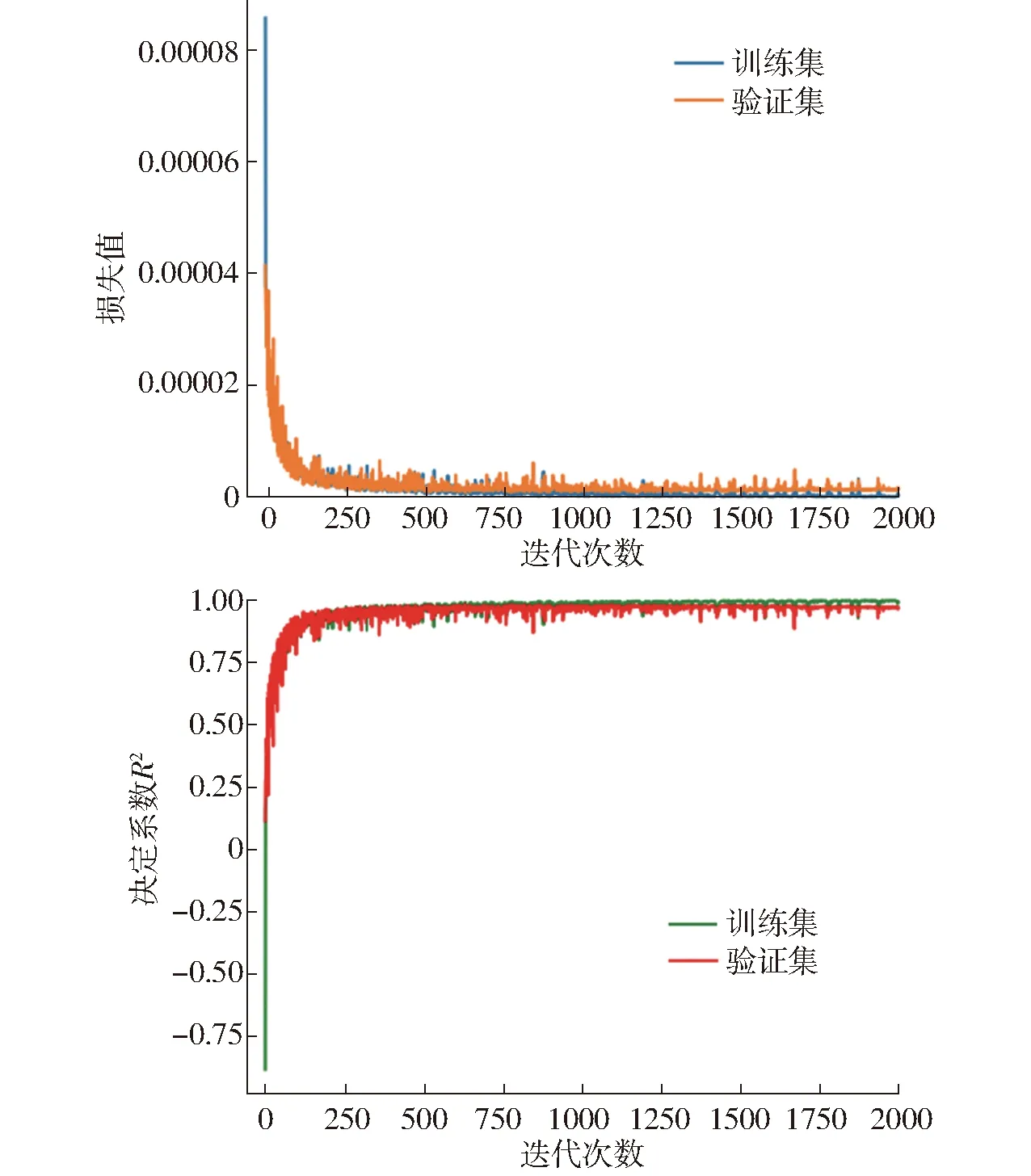
图5 根系半径模型损失和决定系数变化曲线

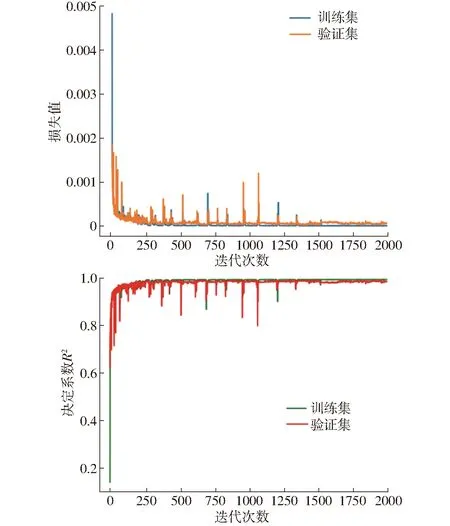
图6 根系深度模型损失和决定系数变化曲线

2.3 仿真数据预测结果

图7为模型在仿真数据上的预测效果，预测使用训练集中不包含的600条仿真数据，当预测值和真实值越相近时，数据点就会越靠近y=x直线，也就表示模型预测效果和拟合程度越优。从图7可以看出，模型拟合程度较好，其中根系深度预测模型拟合程度较好。

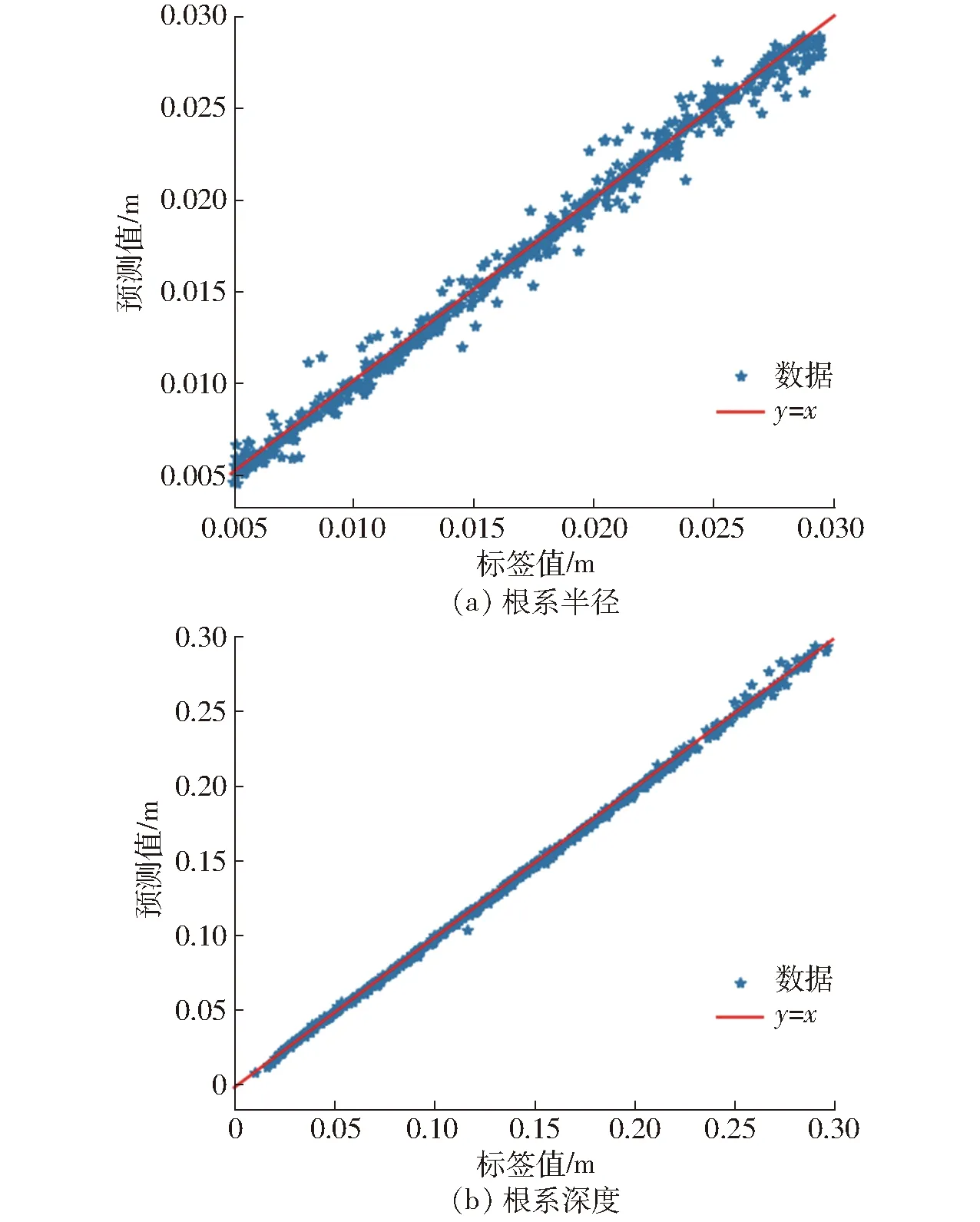
图7 预测结果

将本文提出的预测模型与其他常用回归模型进行比较，比较结果如表2所示。在使用相同训练集和测试集的情况下，本文提出的模型半径预测最大误差为2.9 mm，R2为0.990，均方根误差为0.000 68 m，能够准确预测出树根半径，相较于其他模型，最大误差、决定系数和均方根误差都有明显优势。深度预测最大误差为11.2 mm，R2为0.999，均方根误差为0.002 0 m，虽然决定系数只略高于其他模型，但最大误差和均方根误差明显优于其他模型，说明模型在拟合效果相差不大的情况下，有着更佳的预测精度和预测稳定性。由此可知，本文提出的预测方案在根系半径和深度预测上是可行和有效的。同时，通过训练好的模型，可以实现对根系半径和深度的快速预测，节省了大量人工成本。

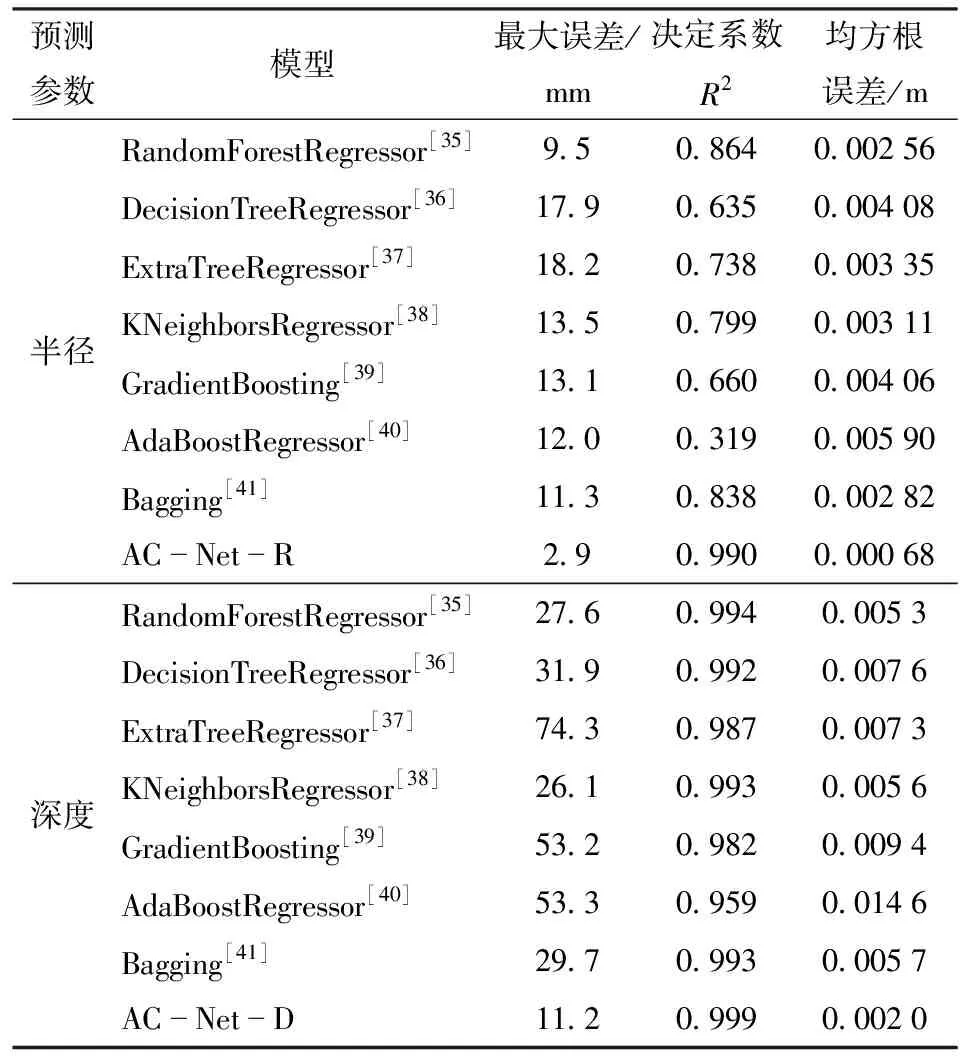
表2 不同模型性能比较

2.4 实地埋根实验预测结果

2.4.1数据采集

为了进一步验证本文预测方案的泛化能力，采用人工埋根的方式采集数据进行测试，实测数据采集使用美国GSSI公司的SIR-3000型探地雷达，如图8所示，雷达天线设置为400 MHz频率。实验场地位于江南大学西北操场沙坑，沙坑土质较为均一，本实验期间未发生降雨，沙土含水率稳定，沙坑实验区域的沙土含水率使用国产FY886型水分测试仪测得，为5.70%，介电常数为4.97 F/m[42]，符合夏季暴晒后干燥沙土的实际情况。同时选择介电常数与活根相近的树枝代替真实根系，并通过测量根的前中后3个位置计算平均值得到根系半径。选取5个半径不同的样本根系作为实验对象，如表3所示，在2个不同深度的实验坑中完成两组实地埋根实验，最后采集到10条A-Scan数据用于测试。

图8 探地雷达检测设备

表3 样本根系数据

图9为深度不同的2个实验坑，其中图9a的深度约为100 mm，图9b的深度约为200 mm，埋入根后单独测量每条根的深度。

图9 实验现场

2.4.2数据预处理

由于实测数据含有杂波，与仿真数据存在较大差别，所以需要通过数据预处理减少噪声对预测结果的影响。如图10所示，图10a为一个树根的实测B-Scan图像，在图中可以明显看到直达波，也就是图中的水平黑带，这是雷达信号未经过反射和折射直接到达地面而产生的波，而在仿真数据中，默认雷达是贴紧地面的，已经消除直达波，所以需要消除实测数据中的直达波[43]，图10b为消除直达波后的效果。图10c为经过标准化后的结果，由于实测数据和仿真数据之间特征取值范围差异较大，因此，经过标准化处理之后，实测数据会在模型上有更好的预测效果，通过对比可以发现，标准化之后的B-Scan图像双曲线变得更加清晰明显，有数据增强的效果。

图10 数据预处理示例

2.4.3预测结果

通过数据预处理后，将实测数据导入之前训练好的模型，得到的预测结果如表4所示，使用本文方案对根系半径预测的最大误差和平均相对误差为1.56 mm、6.45%，对根系深度预测的最大误差和平均相对误差分别为9.90 mm和5.21%，总平均相对误差为5.83%。利用实测数据得到的预测结果表明，提出的方法能成功预测出接近真实值的半径和深度信息。因为实测数据量远小于仿真数据量，所以实测数据预测结果会略优于仿真数据预测结果。2组实验表示样本根系在浅层和深层的预测效果，其中，根系深度单独测量，与实验坑深度相近但不相同，样本根系半径和深度基本覆盖了模型训练集的设定范围。

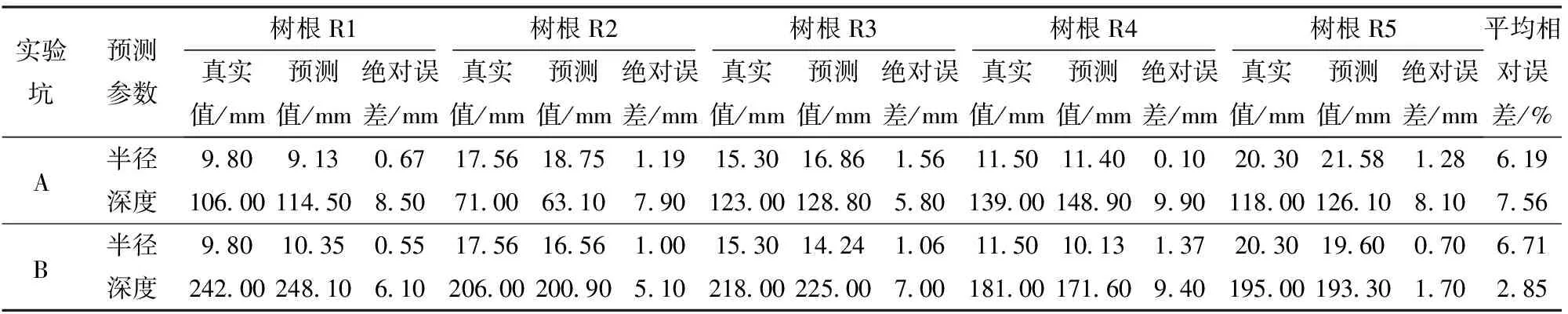
表4 样本根系预测结果

3 讨论

3.1 训练集对预测的影响

训练集很大程度上影响着深度学习模型的性能，优质且数量大的训练集可以明显提升模型预测效果。在训练集中加入真实的A-Scan数据可以提升模型在实测数据上的鲁棒性。一个由真实数据组成、特征空间覆盖全面的数据集能够为相关的研究工作提供极大的帮助和支持。

3.2 雷达频率对预测的影响

高频雷达信号可以有效提升雷达的垂直分辨率，获取更多的地下信息，但在传播过程中会损失大量信号，很难实现对深层根系检测，在浅层根系检测中，高频雷达的优势明显，可以大大降低对细根预测的误差，提升整体预测精度。

3.3 土壤对预测的影响

土壤含水率和同质性会影响电磁波的传播，当土壤含水率较高时，使得土壤相对介电常数升高，其与根系相对介电常数差值变小，反射信号的强度变弱，即在B-Scan中的双曲线变得模糊，降低模型预测精度，而土壤同质性差会产生杂波增加模型预测难度，在图10b中可以看到除反射双曲线外的其他深色区域，这就是由土壤异质产生的杂波。通过大量实验发现，在实地埋根实验中使用干土作为介质会遇到干土结块导致出现大量空气缝隙的问题，空气缝隙的出现会产生杂波增加模型预测难度，因此，为了减小预测误差可以使用含水率较低、材质均一、相对介电常数相近的干燥沙土完成实测数据的采集。

3.4 样本根系对预测的影响

根与土壤的相对介电常数差值越大反射信号越强。在研究过程中发现，使用干枯树枝代替根系所采集到的雷达图像，其反射双曲线非常模糊，甚至难以找到，为双曲线顶点A-Scan数据的提取增加难度，人工标定的准确率降低，而新鲜的样本根系水分含量充足，相对介电常数较高，采集得到的反射双曲线更加清晰。因此，在实地实验中，选用更贴近真实情况的新鲜根系作为实验样本将会减小模型预测误差。同时，本文在训练集中添加了不新鲜根系的样本，以此来增加模型的泛化能力。

4 结论

(1)提出了一种基于探地雷达和卷积神经网络的根系半径和深度预测方法，可实现对根系半径和深度的准确预测。

(2)在仿真实验中，半径和深度预测的最大误差分别为2.9 mm和11.2 mm，远远优于其他常用回归模型；在实测实验中，半径和深度预测的最大误差分别为1.56 mm和9.90 mm，总平均相对误差为5.83%，证明采用本文的预测方案可以准确预测出根系半径和深度。

(3)通过实验发现，相比于B-Scan图像，A-Scan数据包含更多有关半径和深度的信息，且更容易被深度模型学习到，因此，使用A-Scan数据作为数据集更容易训练出精度高、鲁棒性强的根系半径和深度预测模型。从训练数据可发现，本文模型应用范围为根系半径5～30 mm，根系深度 0～300 mm，本文方法适用于双曲线顶点处A-Scan数据，因此，偏离该前提或超出模型应用范围都有可能导致模型预测错误和不稳定。