基于模型预测的插秧机路径跟踪控制算法

迟瑞娟 熊泽鑫 姜龙腾 马悦琦 黄修炼 朱晓龙

(中国农业大学工学院，北京 100083)

0 引言

农机自动驾驶技术是实现精准农业与无人农场的关键与基础，其中路径生成及跟踪是自动驾驶的研究重点[1-3]。路径跟踪是为了使车辆可以自动跟踪由规划算法得到的轨迹路线[4-5]，其主要任务是收集各传感器的信息以确定车辆当前状态(车速、位置、车身姿态等)，然后根据车辆运动学模型或动力学模型，按照所选路径跟踪算法，以车辆当前行驶路径与预设路径的偏差为约束量，计算并输出车辆控制参数，如车速、转向轮转角等[6-7]。

目前，路径跟踪算法应用较多的有纯跟踪控制算法[8]、PID控制算法[9]、神经网络[10]、机器学习[10]、模型预测算法[11]等。其中，罗锡文等[12]采用PID算法进行路径跟踪实验，直线路径跟踪精度平均值小于10 cm，但弯道误差较大；唐小涛[13]提出纯跟踪控制算法，实现对路径的跟踪，但适应性差，需要计算在不同车速下的前视距离；黄沛琛等[14]以固定前视距离下的仿真数据作为样本训练神经网络，实现动态调节前视距离，但是需要大量数据作为训练样本。FAN等[11]将非线性模型预测控制理论应用于车辆轨迹跟踪，其增加了控制量的约束条件，仿真结果表明控制效果更加准确、稳定，且针对影响因素进行了灵敏度分析，实验表明对非线性模型预测控制器的效果影响不大。

农机自动驾驶技术除了满足常规道路运输的行驶控制，还要满足不同作业情况下的行驶要求。农田行驶和作业环境较为恶劣，算法的选取需考虑对环境变化及参数调节的依赖程度，防止当作业环境变化时，无法准确跟踪预设路径或无法及时调节修正算法参数[15]。虽然农机的行驶和作业速度不高，但作业环境复杂，且需满足不同农艺的要求。作业过程中的行驶控制主要体现在对作业路径的跟踪精度及地头转弯的平顺性、安全性要求高[16]。插秧机在我国应用广泛，插秧机特殊的工作环境和插秧农业特点[17-18]对自动驾驶技术的需求更高。模型预测算法可提高自动驾驶响应的及时性和控制过程的平稳性。综上考虑，本文以插秧机为控制对象，以模型预测算法[19-20]为基础设计路径跟踪控制器，以泰勒级数形式对插秧机运动学模型进行线性化处理，利用模型预测算法求解插秧机路径跟踪控制序列，依次循环求解实现对参考路径的跟踪[21]。为确保算法中预测时域略高于控制时域以保证路径跟踪的实时性，根据插秧机车辆参数及特点增加对控制增量的约束条件，以保证插秧机跟踪过程的平稳性。最后通过仿真分析和实车试验进行验证，以证明算法对插秧机自动驾驶控制具有较高的适应性和平稳性。

1 车辆运动学模型及基于模型预测的路径跟踪控制器设计

插秧机运动学模型比较复杂，为了简化模型和便于控制，忽略悬架特性，忽略轮胎与地面的侧向滑动，且假设插秧机左右轮胎在任意时刻都拥有相同的转向角和转速，则可将前后车轮分别集中于一点，插秧机即可简化为二轮车模型[22]。从而减少控制器的在线计算量，提高控制系统的实时性。

车辆运动学模型如图1所示，(xF,yF)与(xR,yR)分别为车辆前轴中心与后轴中心的坐标、δ为前轮(转向轮)转角、θ为车辆航向角、v为车辆后轴速度、L为轴距，在地面固定坐标系XOY下可得车辆运动学方程为

图1 车辆运动学模型

(1)

由式(1)可知，插秧机路径跟踪控制器可看作是由控制量u=(v,δ)和状态量p=(x,y,θ)组成的控制系统。其一般形式可表示为

(2)

基于运动学方程可知，该控制系统为非线性控制系统，无法直接运用模型预测控制算法[23]，故需对上述控制系统进行近似线性化处理。参考轨迹任一点处皆满足式(2)的一般形式，各参数添加下标r代表参考位置的各参考量，则式(2)于参考位置的一般形式可表达为

(3)

式(3)在任意参考轨迹点处进行泰勒级数展开，忽略高阶项，得到

(4)

将式(4)与式(3)相减，可得自动驾驶农机误差模型即线性表达式为

(5)

为了能够将插秧机二轮车模型应用于模型预测控制器的设计，利用前向欧拉公式[24]，将上述线性化系统进行离散化处理可得

(6)

其中

式中k——任一时刻T——采样时间

得到误差模型式(6)后，需基于自动驾驶插秧机线性误差模型设计目标函数，预测插秧机未来时刻的输出。且为了更好地约束控制增量，设

(7)

式中ξ(k|t)——假设k时刻新的状态量

则可推导出下一时刻ξ(k+1|t)的表达式为

(8)

ξ(k+1|t)=Aktξ(k|t)+BktΔu(k|t)

(9)

其中

式中 Δu(k|t)——k时刻的控制增量

n——状态量维度

m——控制量维度t——时间参数

I——单位矩阵O——零矩阵

假设未来预测时域内插秧机状态为ξ(k+1|t)、ξ(k+2|t)、ξ(k+3|t)、…、ξ(k+n|t)，则类比于式(9)，可推导出k+2、k+3、…、k+n时刻的状态方程表达式为

(10)

由递推规律可得自动驾驶系统预测输出表达式[25]为

Y(k)=Ψξ(k|t)+HΔU(k|t)

(11)

其中

式中C——比例系数

NP——预测时域长度

Nc——控制时域长度

由式(11)可知，若已知当前时刻的状态量和控制时域Nc内的控制增量，可以得到预测时域NP的系统输出量且一般情况下满足NP≥Nc。

在目标函数中，控制增量的变化对下一时刻预测状态有极大影响，需依据插秧机自身车辆特性对控制增量进行约束，即

Δumin(k+i)≤Δu(k+i)≤Δumax(k+i)

(i=0,1,2,…,Nc-1)

(12)

转换为

Umin≤AΔUt+Ut≤Umax

(13)

其中

为减少算法运行时间及便于程序的编写，将目标函数转换为标准二次型形式并结合约束条件，求解最优方案为

(14)

式中eT——预测时域内的跟踪误差

R、Q——权重矩阵

ρ——权重系数

求解式(14)后得到控制时域内一系列控制输入增量为

ΔUNc=[ΔukΔuk+1… Δuk+Nc-1]T

(15)

将控制序列中的第一个元素作为实际的控制输入增量作用于系统，即

u(k)=u(k-1)+Δuk

(16)

每周期依次循环，重复上述计算过程，用于预测插秧机未来时刻的输出，实现插秧机对预设路径的跟踪控制，结合约束条件限制，对每个采样周期内的控制增量进行限制，避免被控系统控制量突变的现象，实现快速且平稳地追踪[26]。

2 路径跟踪误差模型

考虑农艺水平的要求，一方面需确保自动驾驶插秧机路径跟踪精度，另一方面需考虑路径跟踪过程中的平稳性。基于模型预测算法设计自动驾驶路径跟踪控制器，以横向偏差d和航向偏差Φ作为评判路径跟踪效果的因素。路径跟踪误差模型如图2所示，横向偏差定义为车辆后轴中心(xcr,ycr)与其在期望路径上的投影点S(xS,yS)之间的距离，规定车辆在参考路径右侧为正，计算式为

图2 路径跟踪误差模型

(17)

式中xcr——平面坐标中车辆后轴中心x轴坐标，m

ycr——平面坐标中车辆后轴中心y轴坐标，m

xS——投影点S处x轴坐标，m

yS——投影点S处y轴坐标，m

先找到期望路径上述投影点S(xS,yS)处的切线，航向偏差计算式为插秧机本身航向与该切线的绝对角度之差，规定顺时针方向为正，计算式为

Φ=57.3(θ-θroad)

(18)

式中θroad——投影点S处的切线航向角，rad

3 路径跟踪算法仿真

在进行实车试验之前，通过仿真对所设路径跟踪算法进行分析。利用Matlab进行算法仿真，因插秧机在田中行走的路径可大致分为直线作业路径、地头转向路径，在仿真环境中分别设计直线与曲线的参考路径，在不同速度下测试所设路径跟踪控制系统对不同路径的跟踪能力。

3.1 直线跟踪仿真

直线路径跟踪仿真基本设定为：插秧机初始状态为X0=0.5 m，Y0=1.0 m，δ=0°，分别以期望纵向速度0.5、1.0、1.5 m/s跟踪参考路径，直线参考路径为直线Y=X，其中X、Y取值范围均为0～20 m，控制周期为50 ms。其余模型预测算法参数如表1所示，在Matlab中编写相关程序，对无人驾驶车辆的直线路径跟踪过程进行仿真。

表1 模型预测算法控制参数

3种车速下直线路径跟踪结果如图3a所示，仿真路线都可迅速跟踪上期望轨迹。图3b为图3a中红色矩形位置偏差较大值的局部放大图，因为初始位置及初始状态与期望值存在偏差，为正常的追踪过程。跟踪过程中实时偏差如图4所示。图4a为横向偏差，在大约X=6 m后误差逐渐趋向平稳，跟踪偏差在0.020 m之内；图4b为3种速度下对应的航向偏差，航向偏差较大值出现在初始跟踪处，最大值为0.500°，在大约X=7 m后偏差值趋向稳定，偏差在0.080°以内。由仿真结果可知，控制器不仅实现了较高精度跟踪期望直线轨迹的功能，也保证了跟踪过程中的平稳性。

图3 直线参考轨迹与实际轨迹

图4 3种速度下横向、航向偏差曲线(直线跟踪)

3.2 曲线跟踪仿真

曲线参考路径设定为

(19)

将插秧机的初始状态设为X0=-1.0 m,Y0=0,δ=0.5°；行车速度分别设为0.5、1.0、1.5 m/s；采样控制周期设为50 ms；控制增量约束及模糊控制器的基本参数设置参照直线路径仿真试验。如图5a中参考路径所示，预设曲线设计为“S”形，目的是验证不同速度下路径跟踪控制器对曲线路径的跟踪能力。

图5 曲线参考轨迹与实际轨迹

曲线路径整体跟踪效果如图5a所示，3种速度下对曲线跟踪在起始点处、中间换向转向处及目标终止点位置出现较大偏差，其余位置跟踪平稳且偏差较小。起始处偏差较大是因为初始状态值与期望值存在偏差，终止点处偏差较大是因为预测时域大于控制时域部分，所做出的预测值超出预设参考路径，都在可接受范围之内。图5b为图5a中红色矩形所示位置的局部放大图，偏差较大。由文献[27]可知，预测算法中参数预测时域NP对路径跟踪精度和稳定性有极大影响，即

dP=vxNPT

(20)

式中dP——预测距离

vx——插秧机纵向车速

在采样时间及纵向车速不变时，预测距离主要与预测时域有关。若预测距离过大，将增大跟踪误差权重，影响插秧机跟踪精度，若预测距离过小，控制量及增量前后时刻相差较大，导致车辆无法及时准确转向。另外，本文针对控制对象所控车速为插秧机后轴实时车速，在插秧机转向时，无法保证纵向速度不变，且预测时域为固定值，故插秧机转向动作发生时，无法实时调参兼顾稳定性与精度。

图6为3种速度下曲线仿真跟踪过程中的实时偏差曲线。由图6可知，3种速度下横向偏差较大值出现在X=-1 m、X=1 m、X=3 m附近，最大值出现在X=1 m附近，最大值为0.580 m，平均值为0.022 m。航向偏差最大值出现在X=1 m附近，最大值为10.570°，平均值为0.699°。结果表明，所设路径跟踪控制器可用于曲线追踪，但设计地头转向曲线时，应避免连续换向曲线设计。

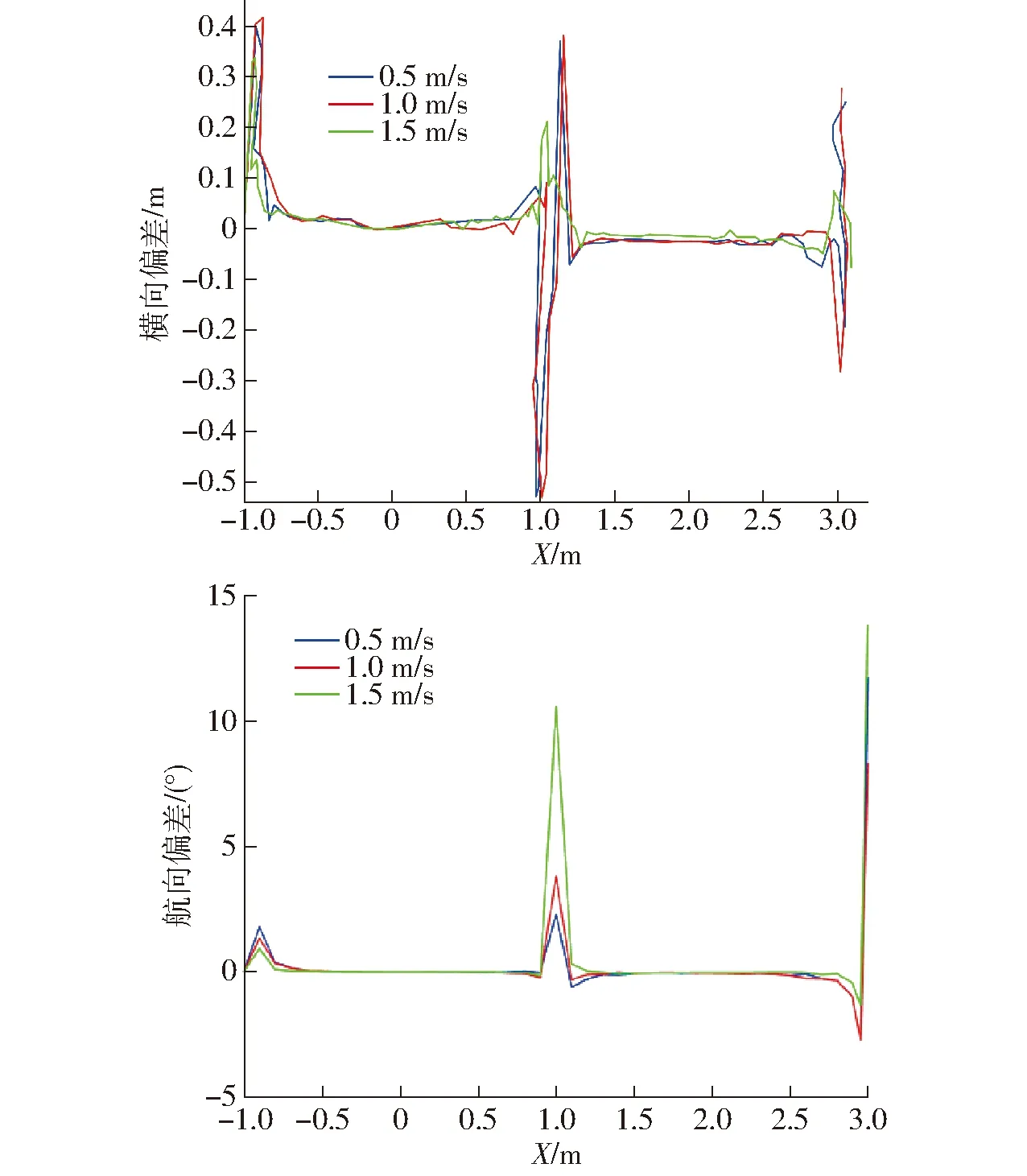
图6 3种速度下横向、航向偏差曲线(曲线跟踪)

4 实车试验

为了验证所建立的基于模型预测算法的路径跟踪控制器的鲁棒性及跟踪精度，以改装后的洋马VP6E型水稻插秧机为试验平台，插秧机参数如表2所示。

表2 洋马VP6E型插秧机参数

平台实物如图7所示，改装原插秧机中的转向系统、行走系统、制动系统：以前轮转角传感器为转向的信息反馈传感器，以无刷直流电机为动力源，通过齿轮传动将动力传输至方向盘及转向轴，实现自主转向功能，以电推杆模拟驾驶员踩、放踏板的动作。同时，该试验平台加入RTK-GPS设备来实现高精度的定位导航功能，增加避障模块，实时检测障碍物[28]以保证自动驾驶插秧机的作业安全。

图7 平台实物图

采集插秧机实际行走的经纬度数据，将参考路径及实车行走的经纬度数据转换为墨卡托投影下的平面坐标数据，并将所有平面坐标数据减去各自第1组平面坐标，绘制实车试验路径跟踪曲线。插秧机由(0，0)出发至终点(14 m，4 m)，由图8可得 3段直线的跟踪效果较好，两段曲线跟踪偏差较大，实时偏差如图9～12所示。

图8 实车试验路径跟踪曲线

图9 实车试验直线横向偏差

图9为实车试验跟踪3段直线路径的实时横向偏差，由表3可得，对直线跟踪的最大横向偏差为0.110 m，平均横向偏差为0.021 m，各组数据小于0.02 m占比不小于69%，表明跟踪过程的平稳性较高；图10为实车试验跟踪3段直线路径的实时航向偏差，由表3可得，航向偏差最大值为10.949°，平均航向偏差为6.187°，小于5°偏差占比不小于71%，表明跟踪过程的实时航向转换变化平缓。

图10 实车试验直线航向偏差

表3 实车试验直线跟踪能力

图11为实车试验跟踪2段曲线路径的实时横向偏差。由表4可得，横向偏差最大值为0.951 m，最小值为0.030 m,平均横向偏差为0.450 m，偏差小于0.04 m占比不小于43%；图12为实车试验跟踪2段曲线路径的实时航向偏差，由表4可得，航向偏差最大值为33.391°，最小值为0.091°，平均航向偏差为10.107°，偏差小于7°占比不小于50%。

图11 实车试验曲线横向偏差

图12 实车试验曲线航向偏差

表4 实车试验曲线跟踪能力

5 讨论

(1)模型预测算法可成功应用于自动驾驶农机的路径跟踪，且对路径追踪的过程中横向、航向偏差值较小且变化平稳。

(2)插秧机为低速车辆，算法可应用于农机不同速度状态下，且不同速度下跟踪结果变化较小，表明算法鲁棒性较好。

(3)实车试验直线部分的跟踪效果略好于曲线部分，仿真试验跟踪效果略好于实车试验。经分析实车试验相比于仿真试验需要考虑机器及导航设备误差等因素，该因素为导致跟踪结果偏差较大的主要原因；在实车试验中，曲线试验误差大于直线试验误差，但追踪过程变化平稳，横向偏差稍大但稳定于约0.4 m。原因为：如曲线仿真结论处所述，预测时域的选取应与插秧机纵向速度、横向速度有关。在直线行驶时，车辆后轴速度理论值等于纵向速度且不变，故预测时域NP虽为固定值，但对直线路径跟踪精度影响较小。当插秧机进行转向动作时，纵向速度实时变化，固定的预测时域NP导致预测距离dP实时变化，将很大程度上影响插秧机对曲线路径的跟踪精度及转向的及时性。另外，转向策略的选取也需考虑插秧机本身转向特性。

6 结论

(1)基于模型预测算法建立了路径跟踪控制器，在参考路径点采用泰勒级数形式线性化农机自动驾驶误差模型，建立控制目标函数，在控制过程中，增加控制量极限约束，保证对路径跟踪的平稳性。

(2)利用Matlab建立3种速度下的仿真试验，结果表明，农机针对直线跟踪的横向偏差可稳定在0.020 m以内，航向偏差可稳定在0.080°以内。针对曲线跟踪平均横向偏差为0.022 m，平均航向偏差为0.699°，表明所设计算法可适用于实车路径跟踪。

(3)以插秧机为试验平台进行实车试验，试验结果表明，该控制器用于自动驾驶插秧机直线路径跟踪时的平均横向偏差为0.021 m、平均航向偏差为6.187°，曲线路径跟踪时的平均横向偏差为0.450 m、平均航向偏差为10.107°。提出的路径跟踪控制算法可成功应用于自动驾驶插秧机对作业行的路径跟踪，且具有较好的鲁棒性及跟踪性能。