自激振动旋耕刀设计与减扭降耗性能分析

肖茂华 钮 约 汪开鑫 朱烨均 周俊博 马如清

(1.南京农业大学工学院，南京 210031; 2.江苏富捷刀业有限公司，盐城 224700)

0 引言

土壤旋耕作业可打碎土层结构，疏松土壤表面，有利于减轻农作物生长发芽的土壤阻力，为作物提供更多的空气与光照条件[1-3]。但作业时土壤条件较差，导致传统旋耕刀阻力大、功耗高[4-8]。方会敏等[9]通过离散元法(DEM)构建出秸秆-土壤-旋耕刀相互作用的三维仿真试验模型，得到了旋耕刀作业时的受力变化规律。刘妤等[10]基于离散元法和多体动力学(MBD)实现了刀辊耕作的仿真分析，并依托土槽试验研究相同工况下刀轴扭矩变化情况，为旋耕刀的相关优化提供了参考。

良好的机械振动可有效减小土壤阻力，提高减扭降耗效果，近年来机械振动理论被逐渐引入到农耕机具中[11-13]。其中，基于自激振动理论的振动深松机构，由于可实现相同降阻条件下更低的功耗，受到国内外专家学者的格外关注[14-15]。MA等[16]根据沿海地区高碱度和高湿度的特点，设计了自激振动式深松机，运用LS-DYNA显式动力学分析软件分别模拟了非振动和振动下的工作过程，分析研究了深松作用机理和土壤的应力变化，以及土壤破碎对土壤振动的作用机理。周华等[17]基于滑切和自激振动减阻的原理，设计了滑切型自激振动深松装置，减阻效果为15.45%～20.05%。RAZZAGHI等[18]选用了新的数学模型来分析一些关键设计参数对振动耕作农具性能的影响，主要引入了无量纲术语以识别设计参数对工具性能的影响。而目前基于自激振动理论设计的旋耕刀研究相对较少。

功率为扭矩和转速的乘积，转速一定时，扭矩越小，功耗越小。为进一步减扭降耗，已有学者对振动式触土农机具的振动特性进行了研究[19]。张倩倩[20]对自激振动旋耕刀在土壤振动切削时的振动加速度信号进行频谱分析，在一定程度上揭示了土壤振动减扭机理。现有文献对自激振动旋耕刀所受阻力、扭矩和振动变化关系的相关研究较少。

本文拟在国标IT245旋耕刀上设计一种自激振动旋耕刀装置，通过运动受力分析，对其大弹簧参数选型与弹簧心轴腰型孔进行设计。借助DEM-MBD耦合仿真，分析自激振动旋耕刀与国标旋耕刀在不同刀轴转速下的三向阻力与扭矩变化情况，然后进行土槽试验验证仿真结果，最终通过对自激振动旋耕刀Y向振动信号的频域分析，探究自激振动旋耕刀减扭降耗的变化规律。

1 自激振动旋耕刀装置设计

1.1 自激振动旋耕刀结构与原理分析

1.1.1整体结构设计

基于多数学者在振动式耕作机械的研究成果以及结合现有国标IT245旋耕刀，采用SolidWorks三维软件对自激振动旋耕刀装置进行三维建模，整个装置如图1所示。

图1 自激振动旋耕刀三维模型图

自激振动旋耕刀主要是由弹簧心轴中的腰型孔与旋耕刀刀柄附加体进行配合，大弹簧一端与旋耕刀刀柄附加体接触，另一端紧压橡胶垫片使其与壳体接触，弹簧心轴两端与壳体采用调节螺母进行配合。通过对调节螺母A与B的调节，实现弹簧心轴腰型孔与刀柄附加体之间轴向相对位置的变化。旋耕刀刀柄孔与孔轴采用间隙配合，小弹簧A、B与刀柄孔轴同心配合且分别位于旋耕刀刀柄与装置外壳之间。旋耕作业时，在大弹簧、小弹簧A以及小弹簧B的作用下，旋耕刀实现绕轴小幅度转动，实现自激振动，装置壳体将整个自激振动旋耕刀进行固定封装。

1.1.2工作原理

固定在刀辊上的自激振动旋耕刀作业时，围绕刀辊做周期性转动，伴随着自激振动旋耕刀在土壤中所处位置的不同，其受阻力与扭矩也在不停变化[21]。为便于分析，将其主要作业状态分为5部分，如图2所示。为了便于比较不同状态的刀具变化，将5种状态的回转半径固定在一条指向作业前进方向的参考线上，图中V为旋耕机工作时的前进速度(m/s)；ω为旋耕机刀轴转速(r/min)；R为自激振动旋耕刀的回转半径(mm)；φ为回转半径与前进方向参考线正向的夹角(刀具相位角，(°))；α为刀柄附加体纵向与大弹簧轴向的夹角(°)；H为最大耕深(mm)。当自激振动旋耕刀刚转动还未与土壤发生接触时，其扭矩与所受阻力近似为0，α1=90°，相位角为φ1，大弹簧处于自然状态。伴随旋耕刀转动，侧切刃先进入土壤中并处于纵向切土状态，随着刀轴继续转动，其扭矩将继续增大，切削阻力从旋耕刀传递到刀柄附加体，使大弹簧产生压缩，α开始减小，α2<α1，相位角为φ2。当旋耕刀处于最大切土深度H时，扭矩将出现最大值，刀柄附加体与心轴腰型孔边缘刚性接触，从而阻止大弹簧进一步压缩，α减小至最小值，α3=80°，此时，大弹簧受压至极限位置，有助于减轻扭矩，降低阻力，相位角φ3=90°。当旋耕刀转过最大耕深后，主、侧切刃慢慢脱离与土壤切削状态，扭矩逐渐降低，此时大弹簧从压缩状态回弹到自然状态，α逐渐变大，α4>α3，相位角为φ4。最后，随着旋耕刀继续转动，主切刃完全离开土层，扭矩逐渐减至0，α5=90°，相位角为φ5，旋耕刀在大弹簧作用下回复到初始位置。需要说明的是，耕作作业的任意时刻，旋耕刀遇到局部坚硬土壤或者石块，根据自激振动原理，旋耕刀可产生相应的偏转和收缩以降低磨损、减小阻力和输入扭矩，即也会压缩大弹簧受压甚至达极限位置，不限于至最大切土深度H一种情况。相位角作为旋耕作业重要的参数，直接影响旋耕刀与土壤的接触状态，导致其所受阻力与扭矩的不同，图中φ取值范围为26°～146°。

图2 自激振动旋耕刀工作状态

1.2 关键部件设计

1.2.1大弹簧参数设计选型

旋耕刀在土壤耕作时主要受到水平、垂直以及侧向阻力，但是水平阻力是最主要的影响阻力，且随着刀轴转速的增加而上升[22]。垂直阻力通过旋耕刀施加力于土壤，其大小主要由耕深决定[21]。旋耕刀所受合力在侧向的分解会得到一个力，这就是侧向阻力。侧向阻力随着转速的增加在一定范围内会产生波动，但是变化程度较平稳。将受力位置选为正切刃，本文中定义自激振动旋耕刀三向阻力方向分别为：水平阻力方向为X向、垂直阻力方向为Y向、侧向阻力方向为Z向。

自激振动旋耕刀在工作时受力分析如图3所示。图中Fx、Fy、Fz分别为旋耕刀受到土壤的水平阻力、垂直阻力与侧向阻力(N)；M为驱动力矩(N·m)。

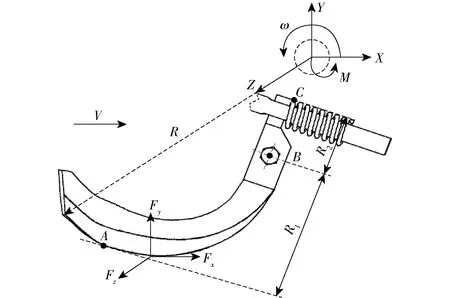
图3 自激振动旋耕刀受力分析图

大弹簧的相关参数是根据作业时旋耕刀所受载荷范围来确定的，旋耕刀在工作中主要受水平阻力的影响，因缺乏不同转速下旋耕刀所受合力分析的相关文献，同时通过自激振动装置原理可得，该装置对水平阻力影响较小，因此本文综合参考水平阻力与合力来确定耕作时旋耕刀所受载荷范围。通过文献[8-9,23]以及前期旋耕刀离散元仿真试验可知，在耕作过程中土壤对旋耕刀主切刃与侧切刃的阻力F的最大值范围为200～300 N。图3中点A为旋耕刀正切刃，点B为旋耕刀刀柄孔圆心，点C为旋耕刀刀柄附加体左下顶点，经过计算得出R1与R2之比约为2.26，根据力学原理，得到大弹簧所受最大载荷F1计算公式为

(1)

式中R1——点A到点B的距离,mm

R2——点B到点C的距离,mm

F——旋耕刀所受阻力最大值,N

通过计算得出大弹簧所受最大载荷F1的范围为452～678 N。在旋耕过程中大弹簧工作应力必须在弹性极限范围内，不能产生永久性变形。

通过前期仿真试验、推导公式计算并依据相关国家标准[24]，最终确定自激振动旋耕刀大弹簧的主要参数为：线径4 mm、节距7.18 mm、自由长度 60 mm、有效圈数7.5、压缩弹簧刚度42.1 N/mm、试验最大载荷756 N。

1.2.2弹簧心轴设计

自激振动旋耕刀耕作过程中，应该保证弹簧在受压时不发生倾斜。随着F1的变化，弹簧在心轴的约束下沿X向运动，起到了限制弹簧在Y向的运动。在耕作过程中通过杠杆原理将旋耕刀刀尖处的阻力传递到刀柄附加体处，再对压缩弹簧进行压缩，从而产生相应的振动位移。由于刀柄附加体在围绕刀柄孔运动过程中产生一定角θ，大弹簧此时受力为其所受阻力在X向上的分力，如图4所示。由于压缩弹簧刚度为42.1 N/mm，试验最大载荷为756 N，而前文分析了大弹簧所受最大载荷F1的最大值为678 N，因此由圆柱螺旋压缩弹簧刚度计算公式可得弹簧变形量[25]，结合旋耕刀受力分析最终得出压缩弹簧在耕作中最大变形量，计算式为

图4 旋耕时弹簧载荷与心轴参数分析图

F2=F1cosθ

(2)

(3)

式中F2——大弹簧在X向所受载荷,N

k1——大弹簧刚度,N/mm

λ——弹簧轴向变形量,mm

由式(3)可知，F2越大，压缩大弹簧X方向变形量λ越大，由上文知F2在678 N时最大，通过计算得出λ最大值约为16 mm。考虑到自激振动旋耕过程刀柄附加体与心轴腰型孔两端面会存在接触碰撞现象，但为防止弹簧过度压缩，腰型孔也要起到限制刀柄附加体转动过大的作用，综合考虑，本装置心轴腰型孔设计总长度L为40 mm，起始状态下，刀柄附加体端面到心轴腰型孔端面的距离L1为15 mm，如图4所示。弹簧心轴主要与大弹簧进行配合，大弹簧的中径设计为22 mm，为了保证耕作时大弹簧能在弹簧心轴上顺畅滑动，弹簧心轴的直径设计为 18 mm。

2 基于DEM-MBD耦合仿真试验

由于自激振动旋耕刀作业时，土壤颗粒受旋耕刀作用力影响，需要采用离散元法进行分析；而仿真过程中弹簧要柔性化处理，需采用多体动力学理论进行分析；目前离散元仿真软件和多体动力学仿真软件均无法单独完成上述仿真试验，故采用DEM-MBD耦合仿真进行研究分析[26]。

2.1 多体动力学模型建立

利用RecurDyn软件实现自激振动旋耕刀在作业时弹簧振动的动力学仿真。以自激振动旋耕刀作业单体为研究对象，通过三维建模软件SolidWorks构建台车模型、旋耕机模型、三点悬挂模型，再将自激振动旋耕刀三维模型与上述模型进行组合装配。

将装配好的模型导入到RecurDyn中，需要对各部件添加合适的约束，添加的主要约束为：左地轮、右地轮、左拉杆、右拉杆和上拉杆分别与台车添加固定副；刀辊和上拉杆分别与旋耕机添加固定副；自激振动旋耕刀与刀辊之间添加固定副。左地轮、右地轮与Ground之间添加Solid接触副；左地轮、右地轮与刀辊以Ground为参考系添加旋转副。在刀辊的旋转副上添加驱动函数，定义驱动类型为Velocity(time)，考虑与EDEM耦合时，生成土壤颗粒期间旋耕机不工作，创建表达式为STEP(time，0，0，t，x1)，含义为0～t内速度为0，t后角速度为x1(rad/s)，以实现刀辊的转动。同理，在左地轮与右地轮的旋转副上也添加驱动类型为Velocity(time)的驱动函数，表达式为STEP(time，0，0，t，x2)，用以实现简化模型的前进运动。

仿真过程中需要考虑重力等因素的影响，需要设置对每个部件的材料属性。在RecurDyn中对本三维模型中的各个零部件材料属性进行设置。旋耕刀的材料类型为65 Mn钢，弹性模量2.1×1011Pa，泊松比为0.3；台车、拉杆、旋耕机、刀辊等材料类型选择45钢，弹性模量为2.05×1011Pa，泊松比为0.29；地轮材料为天然橡胶，弹性模量为1.0×106Pa，泊松比为0.45[27]。

自激振动旋耕刀耕作时，弹簧在土壤切削阻力的作用下产生弹性变形使旋耕刀产生自激振动。当出土后旋耕刀未受到力的作用，此时弹簧形变恢复。自激振动旋耕刀振动来源于弹簧的形变，因此需要将弹簧进行柔性化处理，最终建立自激振动旋耕机刚柔混合体三维模型，如图5所示。

图5 自激振动旋耕机刚柔混合体简化模型

2.2 离散元模型建立

采用EDEM软件进行离散元分析，为兼顾计算机分析时间与仿真效果，土壤颗粒直径设置为 8 mm[28]，采用网格法生产其模型，其密度ρ为 1 850 kg/m3，仿真土槽尺寸为2 400 mm×900 mm×300 mm，土壤颗粒总体数量为3.0×105个。

本次仿真采用Hertz-Mindlin with Bonding模型，此模型在粘结土壤破碎的过程中具有很好的应用效果，它能在土壤颗粒中产生一定的约束，这种土壤间的约束能对土壤产生切向和法向的运动阻力，直到颗粒彼此间的力达到破坏约束作用时，土壤颗粒间才会产生作用。土壤的法向粘结力Fn、法向力矩Mn、切向粘结力Fτ和切向力矩Mτ计算式为

δFn=-υnSnAδt

(4)

δFτ=-υτSτAδt

(5)

δMn=-ωnSnJδt

(6)

(7)

其中

式中A——接触区域面积,m2

Rb——粘结半径,mm

J——截面极惯性矩,m4

Sn、Sτ——颗粒法向、切向粘结刚度,N/m3

υn、υτ——颗粒法向、切向速度,m/s

ωn、ωτ——颗粒法向、切向角速度,rad/s

δt——时间步长,s

模型中主要存在5个粘结参数：颗粒法向粘结刚度Sn、切向粘结刚度Sτ；粘结颗粒法向临界应力δmax、切向临界应力τmax以及颗粒粘结半径Rb。在土壤颗粒半径确定的情况下，通过材料的密度与土壤含水率可得出粘结半径Rb[29]。其余4个粘结参数、各材料性能参数与接触参数如表1所示。

表1 材料性能参数与接触参数

2.3 DEM-MBD耦合仿真试验

在RecurDyn中设置简化模型的前进速度为0.5 m/s，用来模拟旋耕试验的前进速度[30]，调整刀辊高度设定耕深为100 mm，刀轴转速分别为150、200、250、300、350 r/min。

旋耕机工作状态分为正转和反转，参考文献[20]，反转作业时旋耕刀的切土过程是自下而上，在切削张力作用下，土壤强度相对比较低，会更易因破裂而失效，故仿真模型设置为反转。

此外，还需将此三维模型中的自激振动旋耕刀换成国标IT245旋耕刀，重复上述步骤，作为仿真对比试验。最后，将在RecurDyn中生成Wall文件的模型导入EDEM中，并启动激活状态，实现两款软件之间的实时耦合仿真分析。

整个仿真时长设为3 s，共分为2部分：0～1 s内通过颗粒工厂生成仿真所需的3.0×105个土壤颗粒；在1～3 s内旋耕机前进速度设置为0.5 m/s，耕深设置成100 mm，刀轴转速分别设置成上述5种，进行仿真分析。设置数据保存频率为0.001 s，2种旋耕刀对比仿真试验共进行10次，在最后的SOLUTION模块中采集数据，主要截取1～3 s阻力与扭矩数据，进行分析并绘制相关变化曲线，耦合仿真模型如图6所示。

图6 耦合仿真模型

2.4 阻力结果分析

仿真试验得到2种旋耕刀所受三向阻力的变化规律，其随刀轴转动角的变化曲线如图7所示。

图7 2种旋耕刀在5种刀轴转速下三向阻力随刀轴转动角的变化曲线

在5种刀轴转速下2种旋耕刀旋转120°，其水平阻力Fx数值一直为负，因为刀轴旋转方向与旋耕机前进方向相反，且实际受力方向与图3中坐标系反向；垂直阻力Fy呈先正后负的变化规律，主要是旋耕刀在达到最大耕深H的过程中向下切土，刀片受到垂直向上的阻力，与图3标注同向故为正值；当旋耕刀从最大耕深开始出土抛送土壤时，刀片受到垂直向下的力，为负值；侧向阻力Fz恒为正值，因为刀具一直受到内侧面的土壤指向刀体的阻力，且方向与图3标注同向。

自激振动旋耕刀作业时，其绝大部分振动发生在垂直土面的方向上，故重点分析垂直阻力的减阻情况。当刀轴转速为150 r/min时，自激振动旋耕刀垂直阻力较国标旋耕刀降低了1.69%，分别为65.33、66.45 N；当刀轴转速为200 r/min时，垂直阻力降低了5.39%，分别为73.91、78.12 N；当刀轴转速为250 r/min时，垂直阻力降低了6.96%，分别为78.75、85.71 N；当刀轴转速为300 r/min时，垂直阻力降低了10.41%，分别为83.16、92.82 N；当刀轴转速为350 r/min时，垂直阻力降低了3.76%，分别为99.48、103.37 N。

2.5 扭矩结果分析

扭矩变化曲线如图8所示，结果表明，旋耕刀刀轴所受扭矩随着转速的增加而变大，即所需的功耗也会越多。旋耕刀在仿真过程中可分为4个阶段：①在旋耕刀未进入土壤时所受扭矩为0，在刀轴转动下，侧切刃进入纵切状态，随着入土深度增加，扭矩增大，接着主切刃进入横切状态，在主、侧切刃与土壤共同作用时，扭矩出现骤然增加。②当旋耕刀到达最大耕深时，扭矩达到最大值。③旋耕刀越过最大耕深后，主、侧切刃逐渐退出土层，扭矩慢慢减小。④当主切刃完全退出土层时，在此过程中扭矩逐渐减小至0。

图8 2种旋耕刀在5种刀轴转速下所受扭矩变化曲线

不同刀轴转速下，旋耕刀旋转一周所需时间不同，当在低转速下所需时间大于较高转速时，而本仿真中刀轴转速跨度较大，若都采用相同时间段的数据，误差较大。故将数据采集的时间段进行分类，当刀轴转速为150、200 r/min时，数据采集时间段为 1～1.14 s，采集间隔为0.02 s，共71个数据点。当转速为250、300、350 r/min时，数据采集时间段为 1～1.07 s，采集间隔为0.01 s，共71个数据点。最终，通过DEM-MBD耦合仿真得到自激振动旋耕刀与国标旋耕刀的扭矩变化如图8所示。

为进一步分析2种旋耕刀的扭矩规律，对仿真时刀轴扭矩从0到峰值，再到0整个过程中的扭矩取平均值得出平均扭矩，如表2所示。

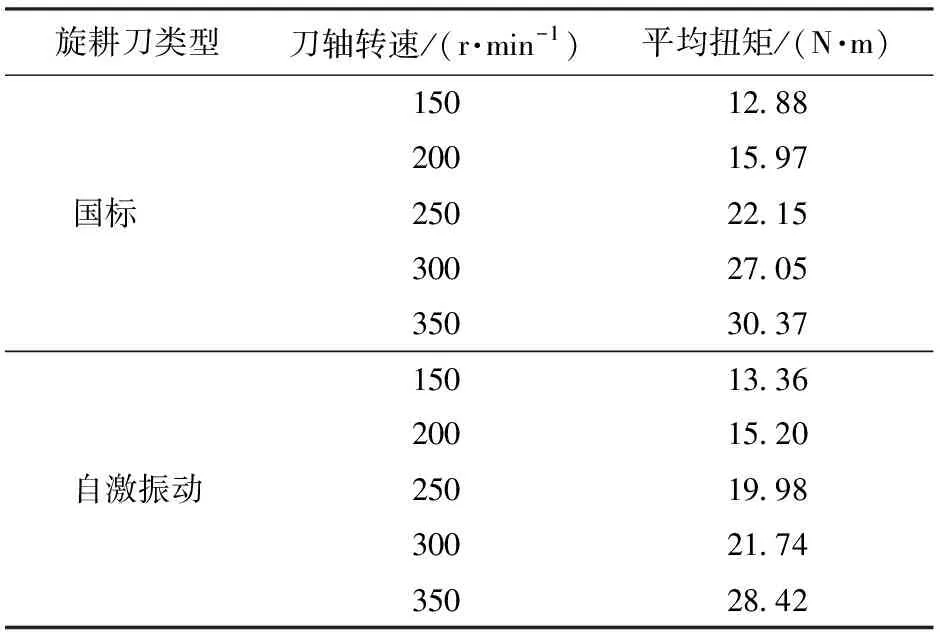
表2 5种转速下2种旋耕刀平均扭矩仿真值

当刀轴转速为150、200 r/min时，自激振动旋耕刀与国标旋耕刀平均扭矩数值相差无几，说明在低转速下自激振动旋耕刀的减扭效果不明显；转速达250、300 r/min时，自激振动旋耕刀的平均扭矩均小于国标旋耕刀，分别下降9.80%和19.63%；转速达到350 r/min时，自激振动旋耕刀相较国标旋耕刀平均扭矩变化不大，下降6.43%。

3 土槽试验

试验系统主要由电机、土槽台车、行走导轨、土槽、旋耕机、传动系统、液压系统、三点悬挂机构、传感器、数据采集系统以及计算机等组成。土槽尺寸(长×宽)为24 000 mm×3 000 mm。土槽台车尺寸(长×宽×高)为2 500 mm×3 000 mm×2 000 mm，其结构简图如图9a所示。

图9 土槽台车结构简图与现场实物图

土槽台车三点悬挂后安装旋耕机，采用江苏清淮机械有限公司生产的1GKN-125型旋耕机。此旋耕机工作幅度为1 250 mm。整机尺寸(长×宽×高)为920 mm×1 482 mm×1 052 mm，作业速度范围为0.83～1.39 m/s，传动形式为中间传动，现场实物如图9b所示。

3.1 土壤参数

土槽内的土壤为黏土(淤泥、黏土和沙质量分数分别为47%、42%和11%)，取自南京市永宁镇。土壤经过调湿、夯实后，控制每次旋耕试验时土壤参数保持一致，土壤平均含水率15%～18%，平均坚实度2.5×105～3.0×105Pa。

3.2 旋耕部分

本文所使用的自激振动旋耕刀装置为本课题组独立设计，自激振动旋耕刀实物如图10所示。单个自激振动旋耕刀装置外壳的尺寸(长×宽×高)为110 mm×100 mm×40 mm。

图10 自激振动旋耕刀实物图

3.3 传感器部分

旋耕试验主要涉及扭矩转速传感器和加速度传感器。土槽台车三点悬挂输出功率主要由动力电机提供，在动力电机输出轴上采用名科扭矩转速传感器，型号为MCK-H001，扭矩量程为1 000 N·m，转速量程为6 000 r/min，精准度为-0.5%～0.5%，环境温度为-20～60℃。

自激振动旋耕刀在耕作时振动数据的采集需要通过加速度传感器，本试验采用维特智能蓝牙无线加速度传感器，型号为WT901BLE5.0C，如图11所示，尺寸为51.3 mm×36 mm×15 mm，量程为(-16～16)g，测量精度为0.01g，数据输出频率为0.1～200 Hz。

图11 无线加速度传感器安装示意图

3.4 试验方法

单次试验在旋耕机的刀辊上安装2把旋耕刀，旋耕机采用反转且刀轴转速设定为150、200、250、300、350 r/min共5挡，前进速度恒为0.5 m/s，耕深保持100 mm，测量自激振动旋耕刀在试验过程中刀轴所受的扭矩与旋耕刀所受Y向振动加速度。而后更换为国标旋耕刀重复上述试验流程。

土槽总长度为24 m，台车运行长度为18 m，试验时土槽两端各留出一定缓冲区，中间10 m为数据采集区。每个作业工况进行3次重复试验，取3次平均值作为每次工况的试验结果。试验现场如 图12 所示。

图12 土槽旋耕试验

4 试验结果分析

4.1 碎土率

为了对比2种旋耕刀不同转速的碎土效果，在测试区内随机选择测试点，以0.5 m×0.5 m的正方形木框在测试区内随机进行取土，用塑料袋封存并标记，在实验室内用标准筛网进行筛选，筛出土块最长边大于4 cm的土块，并求出碎土率[31]，计算式为

(8)

式中C——碎土率,%

M0——0.5 m×0.5 m面积内全耕层所有土块质量,g

M1——0.5 m×0.5 m面积内全耕层最长边大于4 cm土块质量,g

每种转速3组试验结果取平均值后，碎土率数据如表3所示，当刀轴转速为150、200 r/min时，自激振动旋耕刀相较于国标旋耕刀碎土率较为接近，而转速在250、300 r/min时，自激振动旋耕刀的碎土率明显上升，且后者效果更好；转速为350 r/min时，碎土率再度接近。

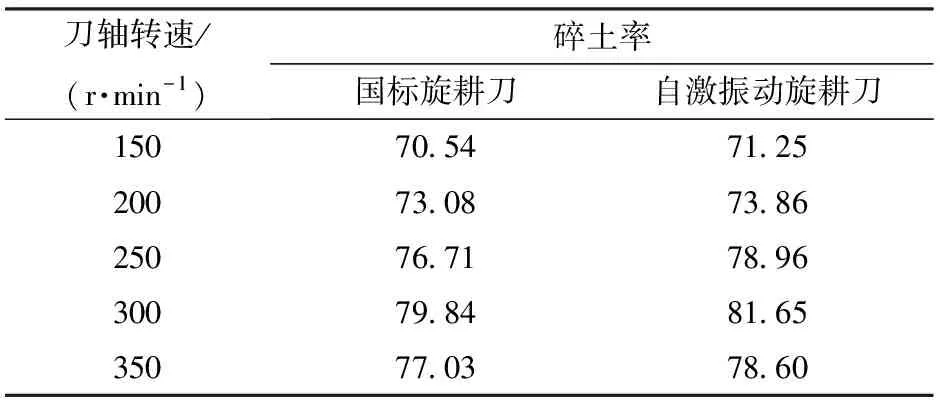
表3 土槽试验碎土率

4.2 平均扭矩

将每种转速的3组试验结果取平均值，得到国标旋耕刀与自激振动旋耕刀的平均扭矩如表4所示。

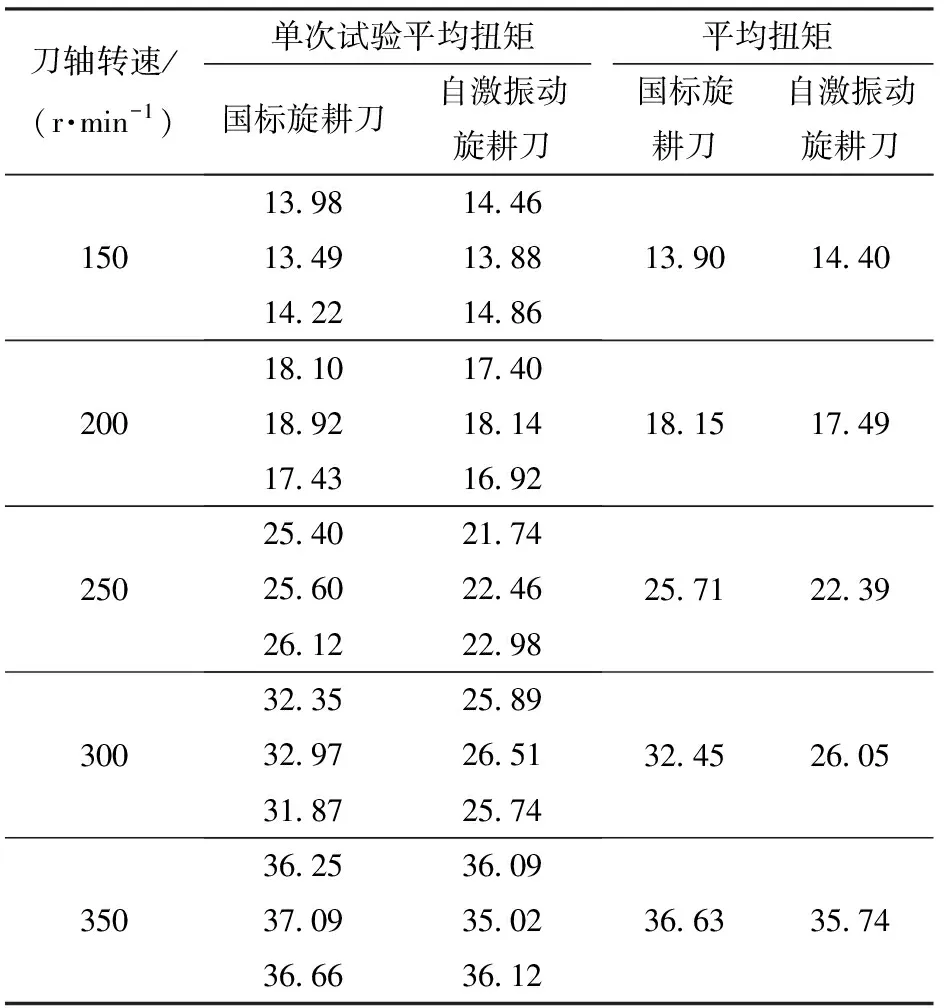
表4 土槽试验中2种旋耕刀所受平均扭矩

由表4可得，作业工况相同时，随着刀轴转速增加，平均扭矩逐渐增大的趋势与旋耕刀实际扭矩变化情况一致。

刀轴转速为150、200 r/min时，土槽试验所得2种旋耕刀平均扭矩接近，说明低转速的降扭效果不明显；转速为250、300 r/min时，自激振动旋耕刀平均扭矩均低于国标旋耕刀，降低率分别为12.91%和19.72%；当转速为350 r/min时，平均扭矩降低率的降幅较小，只有2.43%。

由于土槽台车中各个传动部件间存在摩擦以及干扰扭矩，因此实际试验时采集到的扭矩存在偏差，试验值总是大于仿真值。理想状态下，土槽台车输出扭矩等于所有旋耕刀所受扭矩总和。若将试验中存在的干扰因素近似视为一组常量，故台车采集模块上的扭矩数据近似为刀辊上2把旋耕刀的扭矩之和。

如图13所示，国标旋耕刀仿真与试验平均扭矩变化曲线相关系数为0.997且最大相对误差为16.3%，自激振动旋耕刀的曲线相关系数为0.998且最大相对误差为17.4%，基本验证了构建的DEM-MBD耦合仿真模型的准确性，进一步验证了仿真试验与实际土槽试验结果的一致性。

图13 2种旋耕刀仿真与试验平均扭矩变化趋势

4.3 振动信号频域分析

振动信号的频域分析是指将复杂的信号分割成不同区域段的简单信号，本文主要对自激振动旋耕刀的Y向振动信号进行功率谱密度分析[32]。

为了得到自激振动旋耕刀Y向的固有频率，首先通过ANSYS Workbench对整个装置结构进行模态分析。引入三维模型、设置零部件材料、进行网格剖分后，对刀座添加固定约束，设置模态分析的阶数为6阶，在SOLUTION解算模块中对应每个阶数添加总变形量。通过模态分析可得1～6阶振型的固有频率和最大变形量，如表5所示。

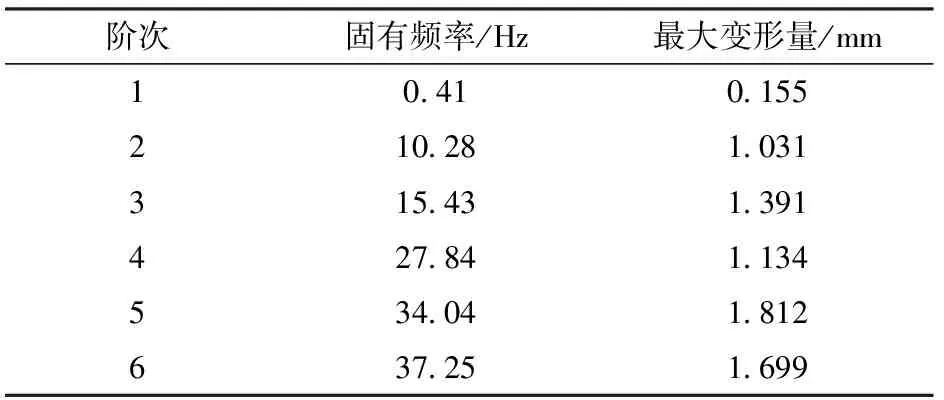
表5 装置模态分析结果

为了验证自激振动旋耕刀模态分析的准确性，将装置固定后对Y向采用锤击法得到其振动加速度信号，再采用快速傅里叶变换(Fast Fourier transform, FFT)得到其固有频率为15.28 Hz，与模态分析时3阶固有频率15.43 Hz较为一致。

由于自激振动旋耕刀装置在耕作时振动主要发生在刀刃垂直土面的方向(Y向)，本文只针对Y向的振动加速度信号进行分析处理。将采集所得Y向的振动加速度时域信号通过Matlab进行数据处理，并通过五点三次平滑法进行平滑预处理，得到更为精确的时域信号图，通过对5种刀轴转速下自激振动旋耕刀Y向振动加速度信号的时域信号图进行功率谱密度分析，可以得到其在各个频率点的功率分布，从而得到能量幅值最大时的频率与其对应的刀轴转速，5种刀轴转速下功率谱密度如图14所示(图中g=9.8 m/s2，作为振动加速度单位)。

图14 5种刀轴转速下自激振动旋耕刀Y向振动加速度功率谱密度

当功率谱密度幅值较大时，其能量也较大，碎土性能好。图14a、14b、14c表明，随着刀轴转速的增加，Y向功率谱密度幅值也在增大，而刀轴转速较低时，激振频率没有达到装置Y向的固有频率，此时没有发生共振，功率谱密度幅值较低。当转速达到300 r/min，激振频率达到装置Y向的固有频率附近时，发生共振，Y向功率谱密度幅值达到最大值，如图14d所示。转速达到350 r/min时，激振频率远离装置Y向的固有频率，此时Y向功率谱密度幅值有所降低，如图14e所示。

4.4 扭矩与振动规律分析

通过对自激振动旋耕刀扭矩与Y向的振动规律进行分析，揭示自激振动旋耕刀减扭降耗的规律。

由振动信号频域分析可知，在刀轴转速为150～300 r/min时，自激振动旋耕刀Y向功率谱密度幅值最大值随着转速的上升而增加，但在350 r/min时有明显降低趋势，平均扭矩降低率与功率谱密度幅值最大值关系如图15所示。

图15 自激振动旋耕刀试验平均扭矩降低率与Y向功率谱密度关系图

由图15可得，5种刀轴转速下平均扭矩降低率与自激振动旋耕刀Y向功率谱密度幅值最大值呈正比关系。在刀轴转速为150～300 r/min时，随着转速的增加，平均扭矩降低率与功率谱密度幅值最大值均上升，且呈正比关系；转速为350 r/min时，平均扭矩降低率和Y向功率谱密度幅值最大值均有所下降。即在刀轴转速为300 r/min时自激振动旋耕刀获得最大能量，故其扭矩降低幅度最大，此时减扭降耗的效果最佳。

5 结论

(1)在国标IT245旋耕刀基础上设计了一种自激振动旋耕刀装置，对自激振动旋耕刀工作原理进行阐述；通过运动受力分析，对自激振动旋耕刀关键部件进行设计，包括大弹簧参数选型与弹簧心轴腰型孔的设计。

(2)采用DEM-MBD耦合仿真技术，对2种旋耕刀在前进速度0.5 m/s、耕深100 mm下的作业过程进行了仿真研究。对垂直阻力与扭矩的仿真值进行分析后得出，刀轴转速为150、200 r/min时，减阻降扭效果不明显。250、300 r/min时，自激振动旋耕刀相比国标旋耕刀的减阻降扭效果较好，垂向阻力分别降低6.96%与10.41%，且平均扭矩降低率较大，分别为9.80%和19.63%，而达到350 r/min时，减阻降扭的效果下降。

(3)在相同工况下开展的土槽试验，获得了5种刀轴下2种旋耕刀扭矩变化的基本规律。对2种旋耕刀在5种刀轴转速下的仿真与试验的平均扭矩进行了分析，得出了国标旋耕刀与自激振动旋耕刀平均扭矩变化曲线的相关系数，分别为0.997与0.998，基本验证了DEM-MBD耦合仿真模型的准确性，进而验证了仿真与土槽试验的一致性。

(4)土槽试验表明，随着刀轴转速的增加，Y向功率谱密度幅值总体呈上升趋势，但刀轴转速较低时，激振频率没有达到装置Y向的固有频率，此时没有发生共振，功率谱密度幅值较低。转速达到300 r/min时，激振频率达到装置Y向的固有频率附近，此时发生共振，Y向功率谱密度幅值达到最大值。当转速为350 r/min时，激振频率远离固有频率，此时Y向功率谱密度幅值有所降低。

(5)土槽试验表明，当刀轴转速150～300 r/min时，随着刀轴转速的增加，平均扭矩降低率与Y向功率谱密度幅值最大值均上升，呈正比关系；当刀轴转速350 r/min时，平均扭矩降低率和Y向功率谱密度幅值最大值均有所下降。综上，当刀轴转速为300 r/min时自激振动旋耕刀获得最大能量，故其扭矩降低的幅度最大，减扭降耗的效果最优。