考虑边界排水时间效应的软土一维非线性固结近似解答

冯 霞，宗梦繁，田 乙，梅国雄，吴文兵,3

(1. 中国地质大学工程学院，湖北，武汉 430074；2. 中国地质大学浙江研究院，浙江，杭州 311305；3. 广西大学工程防灾与结构安全教育部重点实验室，广西，南宁 530004)

软土地基的沉降变形问题一直是地基处理中的一个重点问题，固结理论是其重要的理论基础。1925 年，Terzaghi 首次提出土体一维固结理论[1]，国内众多学者分别从固结方程、初始条件和边界条件等方面对该理论进行了完善。随着实际工程条件的日趋复杂，对一维固结理论的完善工作仍方兴未艾。在Terzaghi 提出的一维固结理论中，假定了土体的压缩系数与渗透系数是常数。实际上，土体的压缩性和渗透性都会随着土体的孔隙比减小而减弱[2−3]。如果忽略这种变化，会使得所得的解答明显高估土体的固结速率。为了描述压缩系数和渗透系数的变化，e-lgσ'和e-lgkv非线性关系被广为应用和发展。DAVIS 和RAYMOND[4]基于e-lgσ'关系，假定自重应力沿深度不变，得到固结系数不变的一维非线性固结解析解。XIE 等[5−7]在其基础上对变荷载下双层以及成层非线性固结模型进行了解答并得到解析解；在此之后，学者们[8−9]先后对循环荷载下的单层和双层非线性固结问题进行求解。但以上针对土体一维非线性固结的研究均假定固结系数不变，而在实际工程中，土体的固结系数并不会保持不变。基于此，BARDEN和BERRY[10]通过考虑e-lgσ'非线性关系，发展了一个简化的非线性一维固结理论，并得到相应的差分解答。MESRI 等[11]同时考虑e-lgσ'和e-lgkv非线性关系，运用有限差分法得到非线性一维固结的数值解答。DUNCAN[12]通过有限单元法对非线性土体的一维固结问题进行了求解与研究。之后，CHEN 等[13]利用DQM(differential quadrature method)求解了成层地基非线性一维固结问题。但是，压缩系数和渗透系数的变化关系是非线性的，直接求解解析解十分困难，以上复杂的数值解在运用方面又存在较大局限性。因此，在保持足够精度的条件下，发展非线性固结近似解具有更大的实际价值。李传勋等[14]和江留慧等[15]基于经典的e-lgσ'以及e-lgkv非线性关系，通过将固结微分方程中的指数项进行简化，分别获得了单层以及双层土体的非线性固结近似解析解，并与差分解答对比验证了所得简化解。卢萌盟等[16]和田乙等[17]根据这种简化方法，先后发展了碎石桩复合地基和排水板地基的非线性固结解答。江文豪等[18]对真空联合堆载预压下砂井地基的固结问题进行了研究，并推导得到了砂井地基的非线性固结解。KIM 等[19]基于Davis 假定，分别推导出瞬时加载和单级加载下成层地基一维非线性固结解析解。

以上研究都是基于边界条件为完全排水或者完全不排水的假设下展开的。但在实际固结过程中，土体的实际边界排水性状是变化的，GRAY[20]最早提出半透水边界并对其展开研究。SCHIFFMAN和STEIN[21]随后也对半透水边界条件下非线性土体固结问题展开了研究，但在过程中发现求解比较复杂且难以得出显式解。基于以上认识，梅国雄等[22]提出在求解过程中考虑边界排水时间效应，利用分离变量法得到考虑边界排水时间效应的连续排水边界下土体一维固结解答。宗梦繁等[23]采用一种多功能大型固结仪，开展了一系列固结试验，得到随时间变化的边界孔压，验证了连续排水边界的合理性，并通过拟合实测的边界孔压，得到相应的边界参数取值。连续排水边界形式简单，能反映孔压随时间的变化，并且可以退化为完全排水和完全不排水边界，因此也得到了众多学者[24−29]的进一步发展和应用。其中，宗梦繁等[26]基于Davis 的假设条件，在解析过程中令Cc/Ck=1，得到连续排水边界条件下考虑非线性的土体一维解析解，但仍未考虑固结系数在实际工程中的变化。之后，又利用有限差分法研究此问题，采用Crank-Nicolson 差分格式对固结方程进行离散后得到求解矩阵，并利用追赶法求得差分解。

为了同时考虑土体在固结过程中渗透性和压缩性的非线性变化，本文引入经典的e-lgσ'以及e-lgkv非线性关系，在连续排水边界条件下，推导出考虑非线性的土体一维固结近似解析解。然后，将所得解答进行退化，验证其合理性。最后，基于所得解详细探讨在固结性状的变化中，界面参数、非线性参数会产生怎样的影响。

1 问题描述

如图1 所示，厚度为H的土层表面作用有瞬时荷载q0，且为无限均匀分布，其排水边界为连续排水边界。假设土体自重应力沿深度不发生改变，记为σ'0，引入经典的e-lgσ'和e-lgkv非线性关系如下：

图1 地基模型示意图Fig. 1 Schematic diagram of foundation model

式中：σ'和 σ′0分别为有效应力与初始有效应力；e和e0分别为土体孔隙比与初始孔隙比；Cc和Ck分别为压缩指数与渗透指数；kv和kv0分别为渗透系数与初始渗透系数。

根据式(1)和式(2)及有效应力原理，可建立土体非线性固结微分方程[14]为：

考虑边界排水性状随时间的变化，固结微分方程求解条件为：

边界条件：

式中，α 和β 为反映土体顶面和底面排水性状的界面参数，α、β 均大于0，α、β 值越大，其对应的排水边界透水性能越好。

初始条件：

式中，q0为瞬时荷载。

在Cc/Ck=1 的情况下，宗梦繁等[26]已获得控制方程满足条件的解析解；李传勋等[14]获得了Terzaghi 排水边界条件下Cc/Ck≠1 时的非线性固结近似解析解。目前基于连续排水边界条件下Cc/Ck≠1时的非线性固结解答研究甚少，本文将对此展开研究。

2 问题的解答

将式(3)进一步展开为：

进一步，按沉降定义的平均固结度Us的表达式如下：

3 解答的论证

3.1 解的退化

当α→∞且β→∞时，固结微分方程的边界条件退化为u(0,t) = 0 和u(H,t) = 0，基于连续排水边界条件退化为Terzaghi 双面排水条件。此时：

同理，将式(45)代入式(34)和式(35)，则可得到退化后的Terzaghi 单面排水条件下超静孔隙水压力u和无量纲参数u的表达式。

将式(43)和式(45)分别代入式(37)，则可以分别求出双面排水和单面排水条件下对应的平均固结度Us；同时，将退化后的双面排水和单面排水对应的u表达式代入式(36)，则可以分别求出双面排水和单面排水条件下对应的按孔压定义平均固结度Up。

3.2 对比验证

与传统固结理论[1]相比，基于经典的e-lg σ′以及e-lgkv非线性关系的一维固结理论可以反映土体非线性的参数Nq的影响。由式(1)、式(2)e-lgσ′以及e-lgkv的关系可以得到：

式中：mv为体积压缩系数；mv0为初始体积压缩系数。

当Cc/Ck趋于1 时，有：

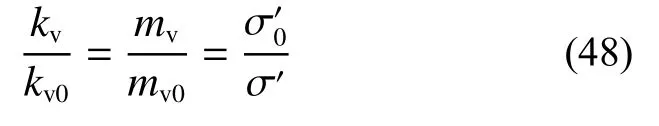
为验证本文解答的正确性，笔者编制了相应的计算程序，在考虑边界排水时间效应的本文解中，分别考虑了Cc/Ck趋于1 时和Cc/Ck偏离1 时两种情况，对本文解与差分解进行对比；再令α=β=1000，此时连续排水边界条件退化为双面排水条件，其余参数保持一致，将本文解答与李传勋等[14]基于Terzaghi 双面排水边界的一维非线性固结近似解析解进行对比。

图2 为本文解与连续排水边界下一维非线性固结差分解答的对比结果。可以看出，当Cc/Ck趋于1，基于本文解得到的孔压分布曲线与差分解的结果相吻合。同时，当界面参数α=β=8 时，土体的孔压消散速率随着Nq值的增大而逐渐减小。图3为Cc/Ck偏离1 时本文解与差分解答的对比结果，可以看出，当Cc/Ck偏离1 时，基于本文解的孔压分布曲线与差分解的结果有细小偏差，但是在合理范围之内。本文解与差分解的对比情况验证了本文解答的正确性。

图2 本文解与差分解的比较Fig. 2 Comparison between degenerated solution and difference solutions

图3 Cc/Ck 偏离时本文解与差分解的比较Fig. 3 Comparison between degenerated solution and difference solutions when Cc/Ck≠1

图4 为退化后的本文解与李传勋等[14]的解答对比结果。结果显示，当α=β=1000，本文解答与李传勋等[14]的解答一致，验证了本文解答的合理性，同时说明了本文解答包含了完全排水边界条件下的解答，更具普适性。从图4 中还可以看出，在完全排水边界条件下，土体边界处的孔压始终为0，不随时间的变化而变化。这是连续排水边界下的一个极端情况，但实际中并不会出现这种情况。

图4 退化后的本文解与李传勋等[[14]]解的比较Fig. 4 Comparison between degenerated solution and Li's solution[[14]]

4 固结性状分析

某土层厚度H=10 m，土体表面无限均匀分布的瞬时荷载q0=100 kPa，土体的初始孔隙比e0=1.5，水的容重γw=10 kN/m3，土的压缩指数Cc=0.6。利用本文解计算不同情况下的土层固结曲线，并对连续排水边界下土层的非线性固结特性进行分析。

4.1 Cc/Ck<1 时Nq 取值对固结性状的影响

由式(48)可知，当本文解Cc/Ck趋于1 时，kv与mv值随Nq值的增大会同步减小。在土体一维固结过程中，kv值越小，则孔压越难消散，土中孔隙水越难排出；而mv值越小，则土体越难进行压缩，土体的孔隙体积难以减小，孔压越容易消散。

但是土的固结系数在实际中并不能完全保持不变，固结系数越大土体固结速率越快，反之固结速率越慢。因此Cc/Ck不会总是趋于1，在Cc/Ck<1 和Cc/Ck>1 的条件下，此时kv和 σ′以及mv的关系为式(46)和式(47)。图5 分析了当Cc/Ck=0.5 时非线性参数Nq值对孔压曲线的影响，同样的，kv与mv值随Nq值的增大会减小，但是mv比kv减小的快，说明在Cc/Ck<1 情况下，压缩系数mv决定着固结过程中孔压的消散能力。由Cc/Ck=0.5 时的孔压曲线也可以看出，土体孔压消散能力是随着Nq值的增大而逐渐增强的。

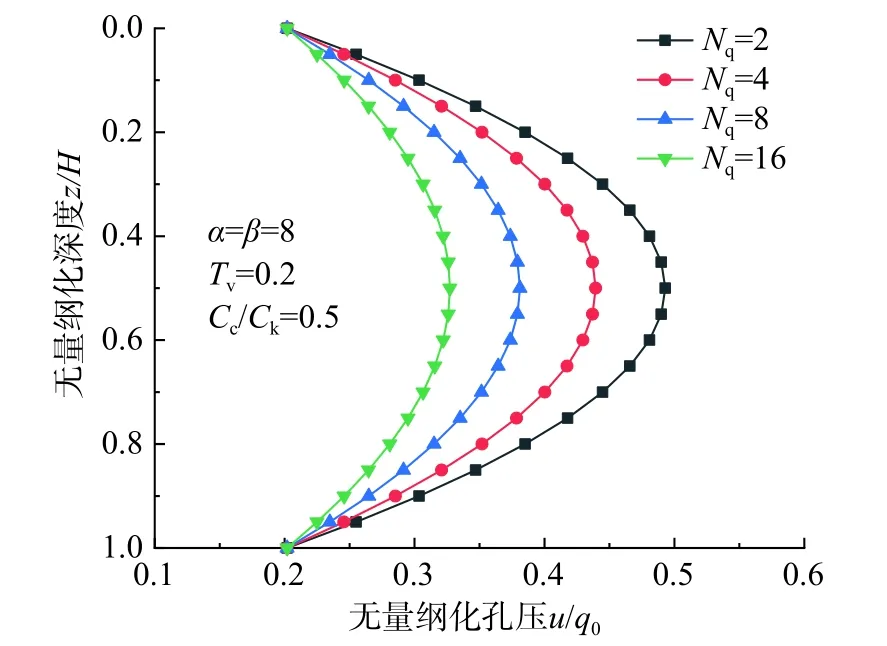
图5 Cc/Ck<1 时Nq 值对孔压曲线的影响Fig. 5 Influence of Nqvalue on pore pressure curve as Cc/Ck<1

图6 和图7 分析了当Cc/Ck=0.5 时不同边界条件下的Nq取值分别对按沉降定义的平均固结度Us和按孔压定义的平均固结度Up的影响。从两张图中容易看出，不论在连续排水边界条件下还是在Terzaghi 单、双面排水条件下，土体的固结速率(包括沉降速率和孔压消散速率)都随着Nq值的增大而加快。在固结前期，连续排水边界条件下的固结速率最小；但在中后期，连续排水边界条件下土体的固结速率超过单面排水下土体的固结速率，而双面排水下的土体固结速率一直最快。对比图6 和图7 发现，Nq取值变化对按沉降定义的平均固结度Us影响明显大于对按孔压定义的平均固结度Up影响，说明Cc/Ck<1 时土体沉降对Nq取值变化更为敏感。

图6 Cc/Ck<1 时不同边界下的Nq 对平均固结度Us 的影响Fig. 6 Influence of Nqon average consolidation degree Us under different boundaries when Cc/Ck<1

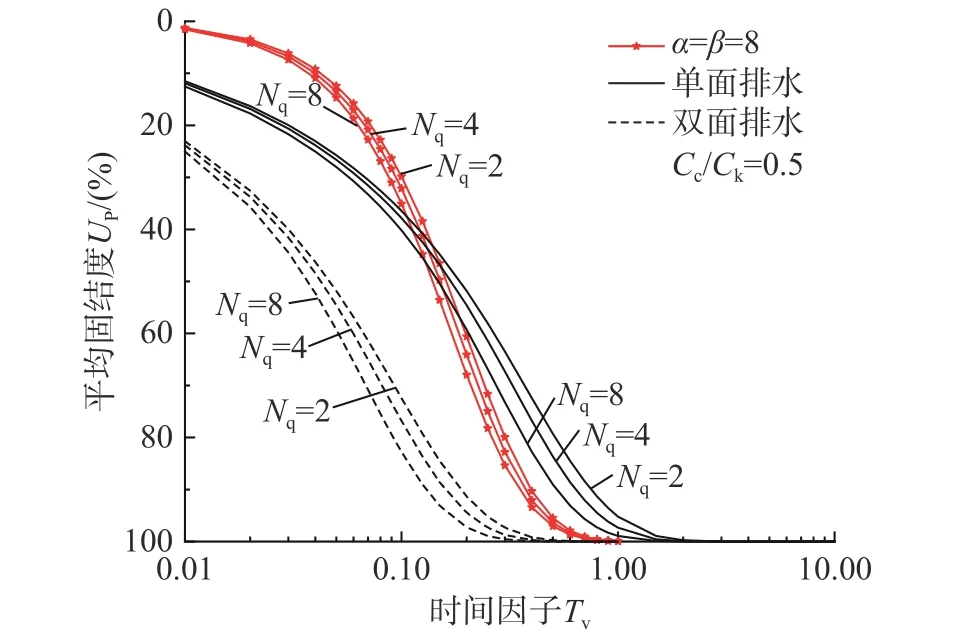
图7 Cc/Ck<1 时不同边界下的Nq 对平均固结度Up 的影响Fig. 7 Influence of Nqon average consolidation degree Up under different boundaries when Cc/Ck<1

4.2 Cc/Ck>1 时Nq 取值对固结性状的影响

图8 分析了当Cc/Ck=1.5 时非线性参数Nq值对孔压曲线的影响，由于Cc/Ck>1，在Nq值的增大时，kv比mv减小的快，说明在Cc/Ck>1 的情况下，渗透系数kv决定着固结过程中的孔压消散能力。因此在Cc/Ck=1.5 时的孔压曲线中，土体的孔压消散能力是随着Nq值的增大而逐渐减弱的。

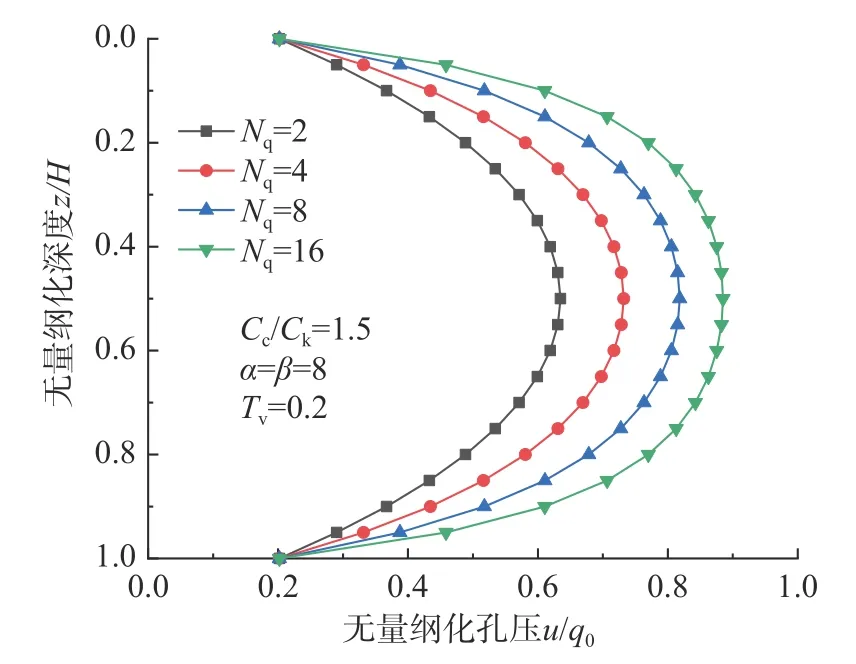
图8 Cc/Ck>1 时Nq 值对孔压曲线的影响Fig. 8 Influence of Nqvalue on pore pressure curve as Cc/Ck>1

图9 分析了当Cc/Ck=1.5 时不同边界条件下的Nq取值对按沉降定义的平均固结度Us的影响。可以看出在Terzaghi 单、双面排水条件下，土体沉降规律与Cc/Ck=0.5 时相反，即土体的沉降速率都随着Nq值的增大而减小。而在连续排水边界条件下，固结前期土体的沉降速率随着Nq值的增大而增大；而在固结后期则相反，土体的沉降速率随着Nq值的增大而减小。

图9 Cc/Ck>1 时不同边界下的Nq 对平均固结度Us 的影响Fig. 9 Influence of Nqon average consolidation degree Us under different boundaries when Cc/Ck>1

图10 分析了当Cc/Ck=1.5 时不同边界条件下的Nq取值对按孔压定义的平均固结度Up的影响，与图9 规律不同的是，三种边界条件下的孔压消散速率都始终随着Nq值的增大而减弱。并且在图9 和图10 的分析中，在固结前期连续排水边界下土体的固结速率最小，而在固结中后期其固结速率逐渐加快，并介于单面排水和双面排水条件之间。同时也可以发现，Nq取值变化对按沉降定义的平均固结度Us影响明显小于对按孔压定义的平均固结度Up影响，这说明孔压消散速率Up对Nq取值变化更为敏感。

图10 Cc/Ck>1 时不同边界下的Nq 对平均固结度Up 的影响Fig. 10 Influence of Nqon average consolidation degree Up under different boundaries when Cc/Ck>1

结合4.1 节和本节内容所述，当Cc/Ck<1 时，土体沉降对Nq取值变化更为敏感；而当Cc/Ck>1时，土体内的孔压消散对Nq取值变化更为敏感。

4.3 Tv 对固结性状的影响

图11 和图12 分别给出了当α、β 相等和不等时，连续排水边界条件下一维非线性固结近似解析解中Tv对孔压曲线的影响。当界面参数α=β时，如图11 所示，孔压曲线在土层深度上对称分布，顶面土层和底面土层反映的透水性能相同，随着时间因子Tv的增大，不论是排水边界还是土体内部，孔压都逐渐减小。而在图3 中可以看出，在Terzaghi 双面排水边界条件下，排水边界上的孔压不随时间因子Tv的改变而变化，其始终保持为0。这是连续排水边界条件与Terzaghi 完全排水边界条件的一个重要区别。

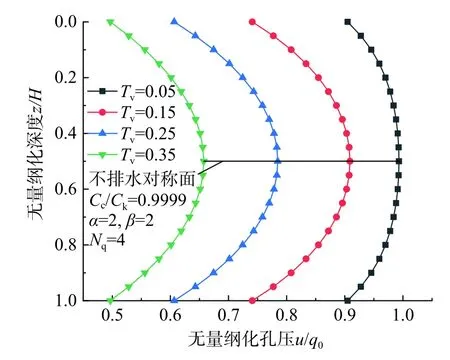
图11 α=β 时本文解中Tv 对孔压曲线的影响Fig. 11 The effect of Tvon the pore pressure curve when α=β in this paper

图12 α≠β 时本文解中Tv 对孔压曲线的影响Fig. 12 The effect of Tvon the pore pressure curve when α=β in this paper

当界面参数α、β 不相等时，如图12 所示，同样的，不论是排水边界还是土体内部，孔压随时间逐渐减小，并且同一时间上半层土内的平均孔压明显要小于下半层内的平均孔压，说明土层顶面的孔压消散速率要大于土层底面的孔压消散速率。因此，界面参数α、β 不相等时，靠近界面参数大的边界的土体孔压消散越快。在此情况下，从图12 可以看出，土层中的不排水对称面位置也随着Tv的变化而变化，但是在图3 的Terzaghi双面排水边界条件下和图11 的连续排水边界条件下界面参数α、β 相等时，土层中的不排水对称面位置是保持不变的。不排水对称面的位置即土体孔压出现峰值的位置。在吹填土地基处理工程中，研究不排水对称面的位置对优化水平排水砂垫层的铺设位置具有初步指导意义[25]。

4.4 Cc/Ck 取值对固结性状的影响

由式(37)，按沉降定义的平均固结度Us的大小受Cc/Ck取值的影响，图13 对比了Cc/Ck取值不同时对基于连续排水边界条件下非线性固结近似解答和基于Terzaghi 双面排水条件下土的非线性固结近似解答的影响。可以看出，不论在连续排水边界条件下还是双面排水条件下，Cc/Ck值越大，土体的沉降发展越慢，反之，Cc/Ck值越小，则土体的沉降速率越快。在整个固结过程中，当其他参数相同时，基于连续排水边界条件下的土体沉降速率一般总是小于双面排水下的土体沉降速率。

图13 不同边界条件下Cc/Ck 对平均固结度Us 的影响Fig. 13 Influence of Cc/Ckon average consolidation degree Usunder different boundaries

图14 对比了Cc/Ck取值对基于连续排水边界条件下非线性固结近似解答和基于Terzaghi 单面排水条件下土的非线性固结近似解答的影响。从图中可以看出，在固结前期，当Cc/Ck取值一定时，连续排水边界条件下的沉降速率小于单面排水下的沉降速率；在固结中后期，当Cc/Ck取值一定时，连续排水边界条件下的沉降速率大于单面排水下的沉降速率。

图14 不同边界条件下Cc/Ck 对平均固结度Us 的影响Fig. 14 Influence of Cc/Ckon average consolidation degree Usunder different boundaries

4.5 α、β 取值对固结性状的影响

图15 反映了α、β 取值对平均固结度Us的影响。通过对比基于连续排水边界条件下的固结度与基于Terzaghi 单、双面排水条件下的固结度，可以看出：在连续排水边界条件下，α、β 取值越大，土体固结沉降越快，其曲线越来越接近双面排水下的曲线，α、β 取值越小，土体的固结沉降越慢，其曲线也越来越偏离双面排水下的曲线；在固结初期，连续排水边界条件下的沉降速率最低，但随着固结过程的发展，连续排水边界条件下的固结沉降速率会超过单面排水下的固结沉降速率，但不会超过双面排水下的沉降速率。在实际工程中，可以通过调整α、β 取值来设计工程中所需要的固结排水速率。

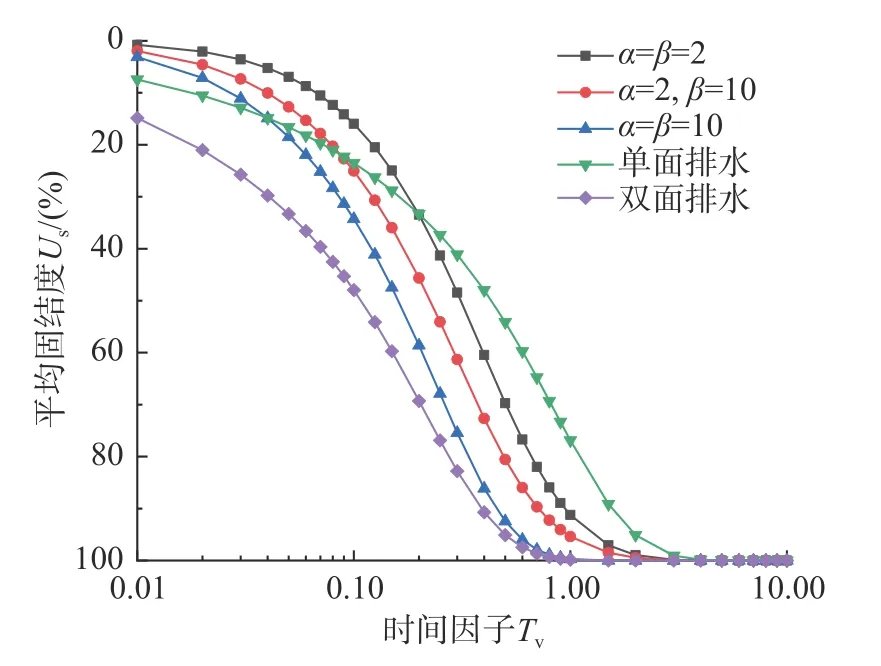
图15 α、β 值对平均固结度Us 曲线的影响Fig. 15 Influence of α and β values on average consolidation degree Upcurve

5 结论

对推导出的考虑非线性的土体一维固结近似解析解同时进行退化和非退化的对比验证，分析各个参数变化对固结速率的影响，得出以下结论：

(1) 在连续排水边界条件下，边界处的孔压随时间逐渐减小，最终消散至0。而在Terzaghi 完全排水边界条件下，边界处的孔压始终为0，这是连续排水边界的一种特例。本文考虑排水边界时间效应得到的饱和土体一维非线性固结近似解答，能成功退化到既有的基于Terzaghi 排水边界下的解答，是一种更具一般性的解答。

(2) 在连续排水条件下，土体内的不排水对称面的位置与界面参数有关，并且随时间会发生变化。当界面参数不相等时，不排水对称面更靠近界面参数小的一侧，并随着时间增大向更靠近该侧的方向移动。而Terzaghi 排水边界条件下的不排水对称面的位置始终保持不变。

(3) 当Cc/Ck>1 时，在固结前期，土体的沉降速率随着Nq值的增大而增大，而在固结后期则相反，这与Terzaghi 单、双面排水下沉降速率随Nq值的变化规律不同。

(4) 在连续排水边界条件下，土层界面参数α、β 取值越大，土体的孔压消散能力越强；α、β 取值越小，土体的孔压消散能力越弱，并且α、β 对土体固结的影响很大，因此在土体固结分析中，考虑边界条件的时间效应十分重要。