基于机器学习和大数据的山洪预测模型研究

刘明锦，张智涌∗，王 宾，陈万林

(1.成都水生态文明建设研究重点基地，四川 都江堰，611830；2.四川水利职业技术学院，四川 崇州，611231)

0 引言

山洪灾害是世界上危害最大的自然灾害之一，具有突发性强、破坏力大、难以预测等特点，容易造成大量人员伤亡、严重的财产损坏和环境灾难。由于自然地理环境、极端灾害天气以及社会经济活动等各类因素的共同影响，造成了我国的山洪灾害问题呈现出频发、多发的态势。1950－2016年间，我国山洪灾害造成的直接经济损失高达1.72×105亿元，2000年以来，每年因为山洪死亡的人数超过1000人[1]。山洪灾害的防御工作是我国防汛减灾工作的重点与难点。及时、准确地进行山洪灾害的预警预报工作，有利于指导受灾群众快速撤离、减轻灾害损失、保障人民的生命财产安全，是目前最为有效可行的防灾减灾非工程措施，是山洪灾害防御的重要研究方向。

为了对山洪进行精准预测，不同领域的国内外学者近年来从多个不同的角度进行了很多有意义的研究[2]。由于山洪和强对流降水的密切关系，气象类的学者更倾向于对触发山洪的强降水检测进行研究[3]；水文地质防汛等领域类的学者则倾向于采用水文类临界雨阈值以及一些较为稳定的水文汇流模型来进行计算，其本质上也依赖于气象信息[4]；随着计算机建模的兴起，也有学者利用需要进行山洪预测的计算机进行建模，考虑地形、地质条件等因素，结合气象信息对山洪进行预测分析。

总的来说，目前主流的山洪预测的核心思想还是结合各地区影响暴雨洪水的各类相关资料(历史水文数据、气象类、地形地貌数据等)，研究其规律并建立的相关经验关系。在以往的研究中，大多以山洪成因的各类影响因素为初始条件，用历史数据作为主要参考对象，从而根据不同的水文地质环境建立山洪预测模型。该类模型针对性较强，有历史数据支撑，但本身存在模型灵活度不高、历史数据准确性等问题，因此，山洪数据预测值误差较大。同时因为各地区环境不一样，山洪成因不同，因此存在模型迁移难度大的问题。

区别于以往侧重于气象资料或者计算机建模模拟山区构造等进行的山洪预测，本研究的意义在于引入了机器学习模型，利用传感器实时采集的降雨量作为输入(采集时间可以设置较小的时间片)和最终形成的洪水量进行实时比对，形成大数据，通过机器学习模型不断校正不同情况下降雨量与山洪之间的关系，最终能够生成一个趋于理想条件的洪水预测模型。本研究期望利用机器学习和大数据技术为山洪预测提供技术支撑。

1 研究区域情况及数据来源

研究区域位于四川省阿坝州小金川流域。小金川河是大渡河的一级支流，流域面积5275km2，有北、东两源。北源为抚边河，在猛固桥处与东源沃日河汇合后，始称小金川河，该处流域面积3681.95km2。猛固桥往下，河谷逐渐拓宽，水流趋缓，水量大增，两岸集镇、耕地、人口增多。其间分布有小金县城(美兴镇)、新格乡以及丹巴县的太平、半扇门、岳扎和中路四个乡，总长60.8km，落差472.6m，平均比降7.8‰，小金川河分属小金县和丹巴县管辖。分界线位于三叉沟口，上段属小金县，该处集雨面积4751.8km2，猛固桥到三叉沟，河段长26.51km，总落差143m，平均比降5.39‰，河道较为平缓。河谷多呈“U”形，河道弯度小，耕地和居民多分布于两岸阶地、滩地。本段汇入的支沟众多，其中集雨面积大于100km2的有左岸的美沃沟、沙龙沟以及右岸的崇德沟和水卡子沟。其流域内共有小金水文站、达维雨量站和两河雨量站，其中小金水文站有完整的雨量数据和流量数据。研究区域基本情况见图1。

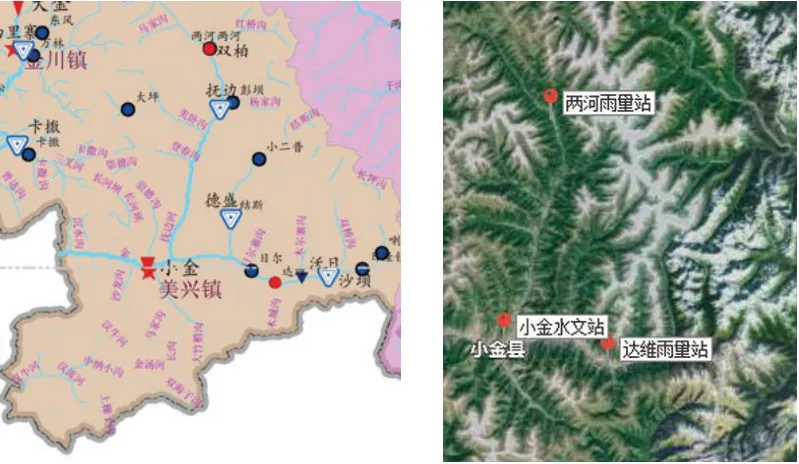
图1 研究区域基本情况

根据阿坝州水文局提供的采集样本中的历年雨量数据和山洪数据，取2013年5月1日后开始的数据。其中，小金水文站的雨量数据5343条，达维雨量站雨量数据5961条，两河雨量站数据2339条，小金水文站流量数据有26759条，如表1所示。其中由于前期时间采集不一致和流域内降雨时间和降雨量不相同，因此，雨量数据和流量数据产生条目不一样，雨量站之间多是因为雨量不同而导致雨量条目不一致。

表1 研究区域基础数据

经过数据分析，发现部分数据中出现异常流量，排除掉因为梯级电站放水等异常流量，取当日中高段雨量为基准，筛选出研究数据，如表2所示。

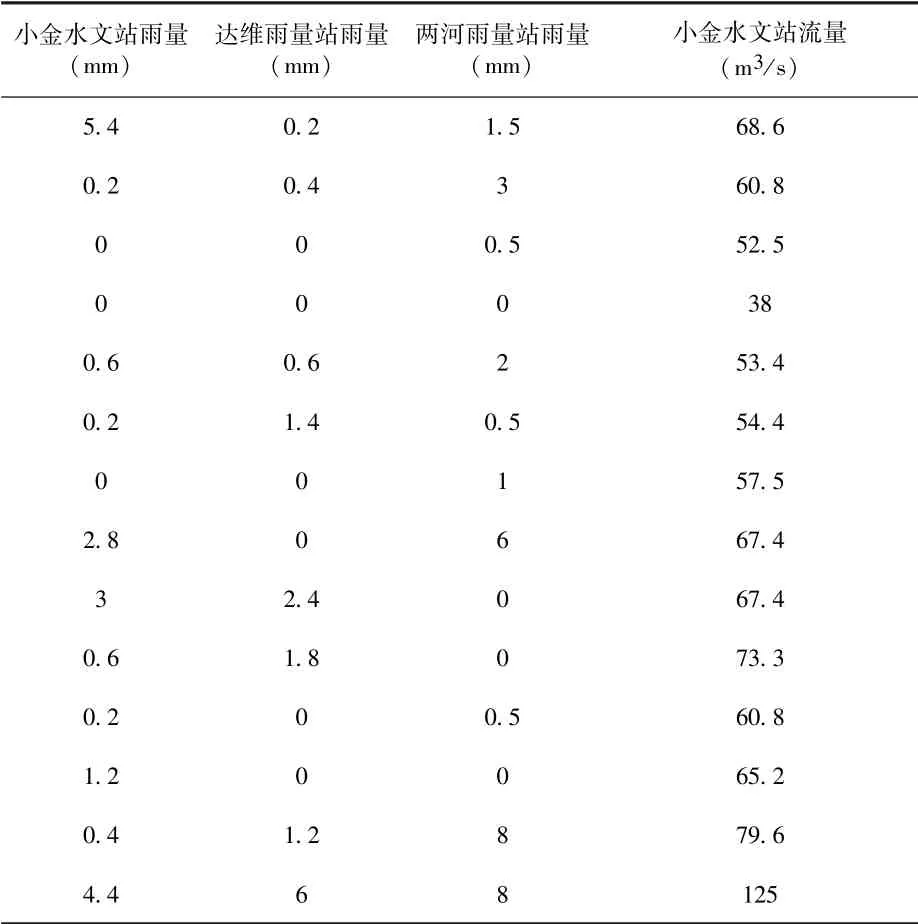
表2 研究区域雨量

2 系统设计思路

本研究的设计思路是建立一套具有适用性广、不限制区域的山洪预警模型。建立模型首先需要考虑山洪形成的原因。

根据国内相关学者的研究，山洪的成因与降雨量有着密切的关系，随着降雨量的不断增多，不同下渗率的土壤湿度逐渐饱和，达到山洪爆发的临界雨量，根据地质地形的不同，山洪的形成时间会有所不同[5－6]。根据流域面积的不同，降雨与最终汇流成山洪有一定的时间差。

因此，可以看出，降雨是山洪爆发的最主要成因[7]，考虑到山区存在着资料匮乏等问题，在系统设计上尽量简化以往需要考虑的其他各类因素影响[8]，设传感器数据关系参数W1、W2…Wn来替代各类以往山洪计算中需要考虑的地形数据、地质数据、土壤湿度指数、下渗率、山洪与降雨的时间差以及其他孕灾环境指标等山洪影响系数，降雨量为x和山洪水量y从传感器中实时获取并存入大数据平台。系统设计思路如图2所示。

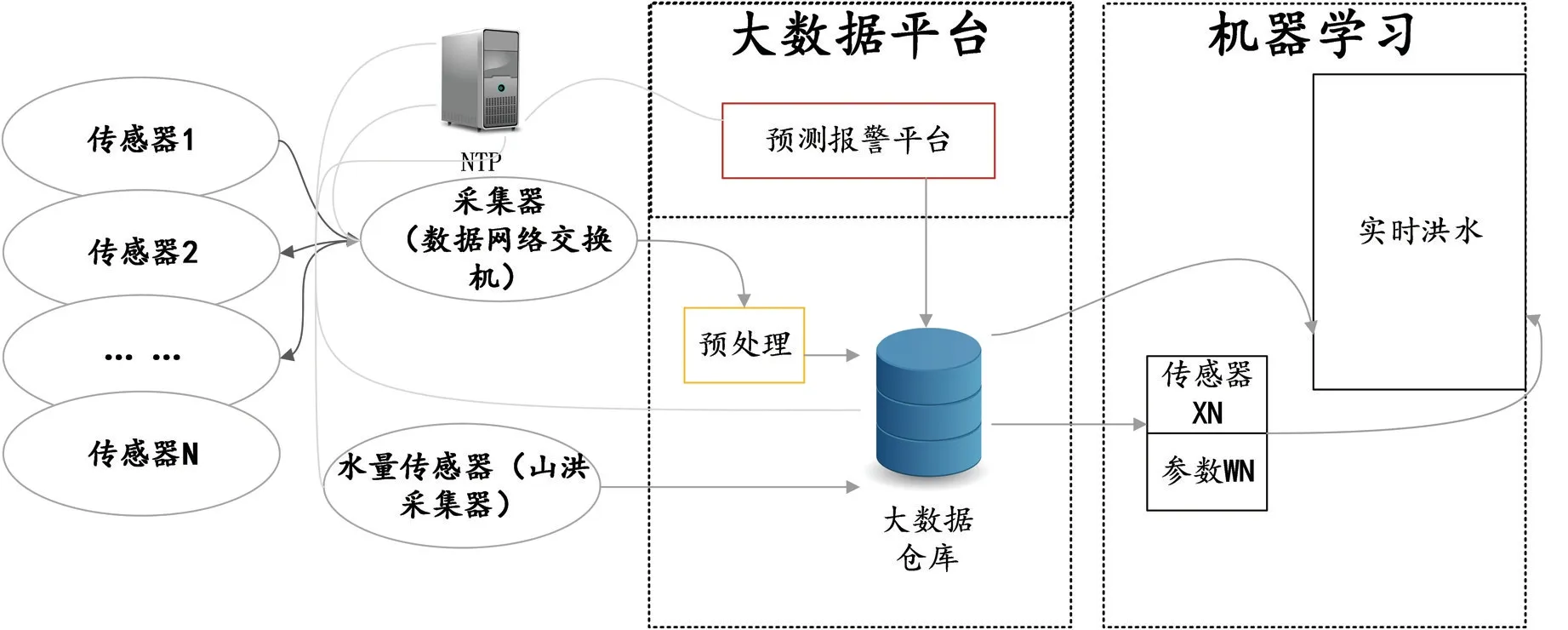
图2 系统设计思路

模型中通过NTP服务器进行数据时间同步，保证所有平台的数据时间步调保持一致。传感器采集的实时数据x通过采集器传输到大数据中心进行存储，本研究利用山洪预警模型机器学习算法，来计算各类传感器中获取的降雨量的实时数据x与最终汇流的山洪流量y之间的关系参数W。在不断的采集过程中，大数据平台会积累大量传感器数据，山洪预警模型机器学习算法利用这些大数据来不断优化关系参数W，使其精度越来越高，从而形成一个不断诊断与改进的数据优化螺旋上升模型。

3 山洪预测模型

3.1 山洪预测模型参数

根据山洪形成的主要因素，给定一个大小为n的数据集Yi，xi1，xi2…xid(i＝1，…，n)，其中xi1…，xid是在山洪预测中第i个传感器属性的取值，yi为待预测的山洪值，即模型的预测目标，预测目标yi与传感器之间的关系为线性假设组合，则之间的关联公式为:

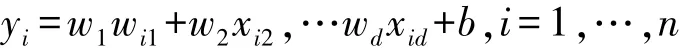
该式也是山洪预警模型中机器算法公式，其中w1，w2…，wd，b均为影响因素，w表示权重，b表示偏重。

3.2 山洪预测优化

用yi表示为预测的山洪值，即模型的预测目标，y表示真实值。预测目标值与实际值是不一样的，在这个模型中未知的影响因素为w1，w2…，wd，b，即要计算和优化的目标。通过计算和优化影响因素w1，w2…，wd，b，使其无限接近实际值y。

为了计算和优化影响因素w1，w2…，wd，b，引入损失函数(Loss Function，或Cost Function)概念。通过传感器采集的实际值与模型的预测值进行比对，损失函数输出一个非负数的实值，这个实值表示模型误差的大小，公式如下:其中，y＾

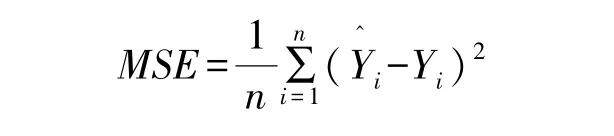
i表示预测值，yi表示实际值，即对于一个大小为n的数据集，MSE是n个数据预测结果误差平方的均值。损失函数计算出来之后，需要通过不断地优化。优化方式采用梯度下降法:设如果fx在点xn有定义且可微，则认为fx在点xn沿着梯度的负方向－f(xn)下降是最快的。反复调节xn，使得fx接近最小值或者极小值，调节的方式为:

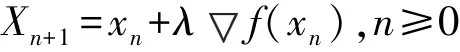
上式中，λ代表学习率。

4 机器学习模型训练

定义了山洪预测模型结构之后，通过以下几个步骤(见图3)进行机器学习的山洪预测模型训练:

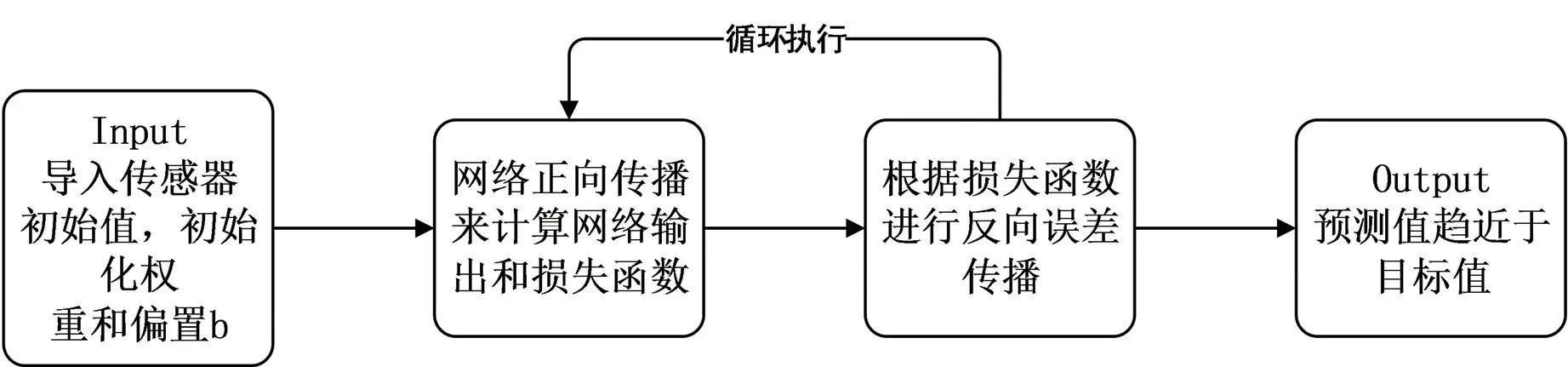
图3 机器学习流程

(1)采集传感器数据初始值，初始化权重wi和偏置b参数值；

(2)利用网络正向传播来计算网络输出和损失函数；

(3)根据损失函数进行反向误差传播(backpropagation)，将网络误差从输出依次向前传递，并更新网络中的参数；

(4)重复2－3步骤，直至网络训练误差达到预期值，即预测值趋近目标值为止。

训练程序的代码配置如下:

＃准备样本特征X，训练初期用dawei，lianghe，xiaojin作为样本特征

x＝data[[′dawei′，′lianghe′，′xiaojin′]]

＃接着用xiaojinshuiliang作为样本输出y

y＝data[[′xiaojinshuiliang′]]

＃划分训练集和测试集

from sklearn.model＿selection import train＿test＿split

x＿train，x＿test，y＿train，y＿test＝train＿test＿split(x，y，test＿size＝0.2，random＿state＝0)

＃查看训练集和测试集的维度

＃print(′x＿train.shape:′，x＿train.shape)

＃print(′x＿＿test.shape:′，x＿test.shape)

＃print(′y＿train.shape:′，y＿train.shape)

＃print(′y＿test.shape:′，y＿test.shape)

＃从sklearn库中导入函数

from sklearn.linear＿model import LinearRegression

＃执行函数获得一个模型

LR＝LinearRegression()＃未经训练的机器学习模型

＃对模型传入输入数据x＿train和输出数据y＿train

LR.fit(x＿train，y＿train)＃经过训练的机器学习模型

＃输出截距和各个系数

print(′LR.intercept＿:′，LR.intercept＿)

print(′LR.coef＿:′，LR.coef＿)

＃评价模型。这里使用MSE和RMSE来评价模型的好坏

y＿pred＝LR.predict(x＿test)

＃引入sklearn模型评价工具库

from sklearn import metrics

print(″RMSE:″，np.sqrt(metrics.mean＿squared＿error(y＿test，y＿pred)))

import matplotlib.pyplot as plt

fig，ax＝plt.subplots()

＃画散点图

ax.scatter(y＿test，y＿pred)

ax.plot([y.min()，y.max()]，[y.min()，y.max()]，′k－－′，lw＝4)

＃设置标题

ax.set＿title(′Plot′)

＃设置X轴标签

ax.set＿xlabel(′Measured′)

＃设置Y轴标签

ax.set＿ylabel(′Predicted′)

＃显示所画的图

plt.show()

为了更好地进行机器学习训练，将数据集分割为两份:一份用于调整模型的参数，即进行模型的训练，模型在这份数据集上的误差被称为训练误差；另外一份被用来测试，模型在这份数据集上的误差被称为测试误差。训练模型的目的是通过从训练数据中找到规律来预测未知的新数据，所以测试误差是更能反映模型表现的指标。

分割数据的比例主要考虑以下两个因素:更多的机器学习训练数据会降低参数估计的方差，从而得到更可信的模型，即传感器采集的数据越多，计算越精准；而更多的测试数据会降低测试误差的方差，从而得到更可信的测试误差。

5 结果验证

结果验证是利用python的sklearn深度学习框架平台来进行数据的验证和仿真。在仿真过程中，输入了一系列传感器数据集和相应的山洪数据集来进行模型的训练和预测。下面的散点图展示了使用模型后对山洪数据的预测。其中，在XY轴中横坐标X表示当前情况下的山洪实际情况，纵坐标Y表示根据山洪预测模型预测的结果，当二者值完全相等的时候就会落在虚线上。所以模型预测得越准确，则点离虚线越近。

模型在运行时间T1之后的结果变化如图4所示，程序运行结果如表3所示。

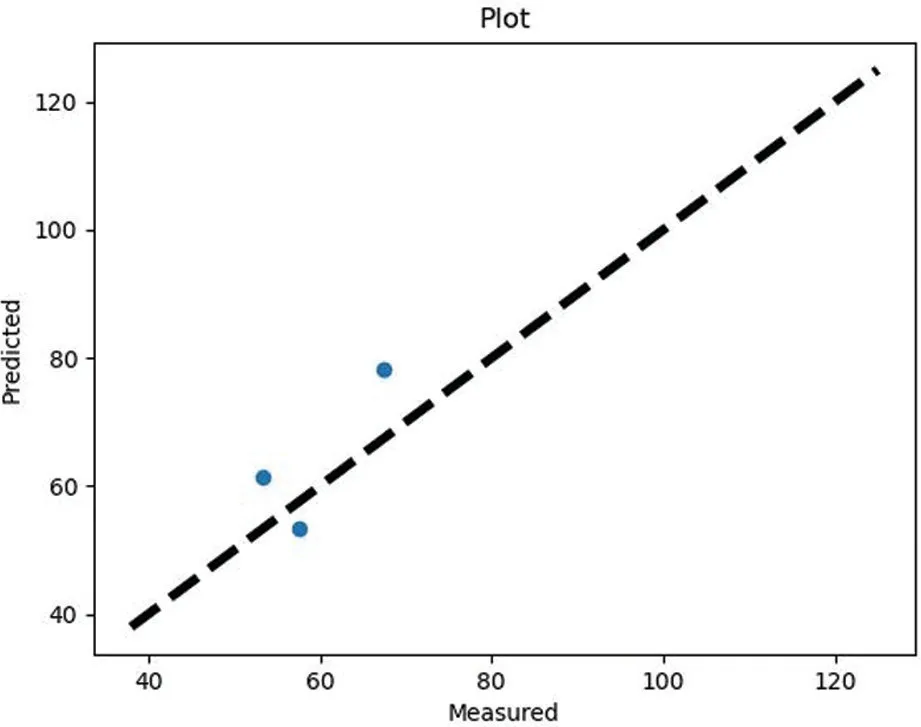
图4 模型在运行时间T1之后结果变化

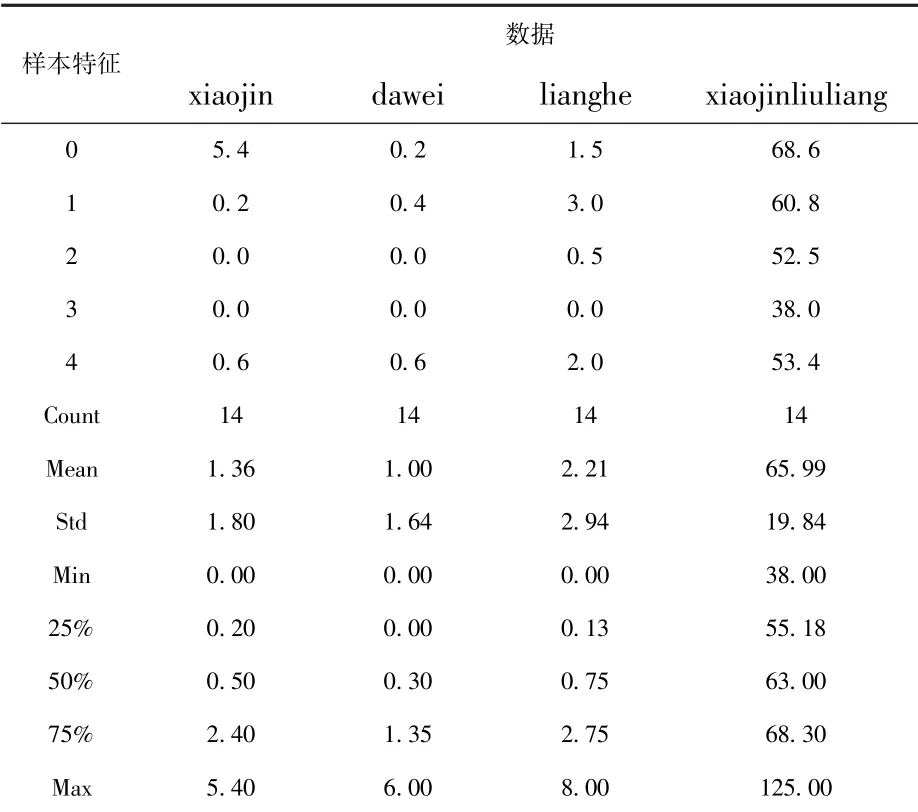
表3 模型运行时间T1数据

LR.intercept＿:[51.43598567]

LR.coef＿:[[2.66256014 7.81232586 1.88804097]]

RMSE:8.15

将小金水文站5343条数据，达维雨量站5961条数据，两河雨量站2339条数据以及小金水文站流量数据26759条数据放入模型中进行机器学习，最终模型运行时间T2的结果变化如图5所示，程序运行结果如表4所示。

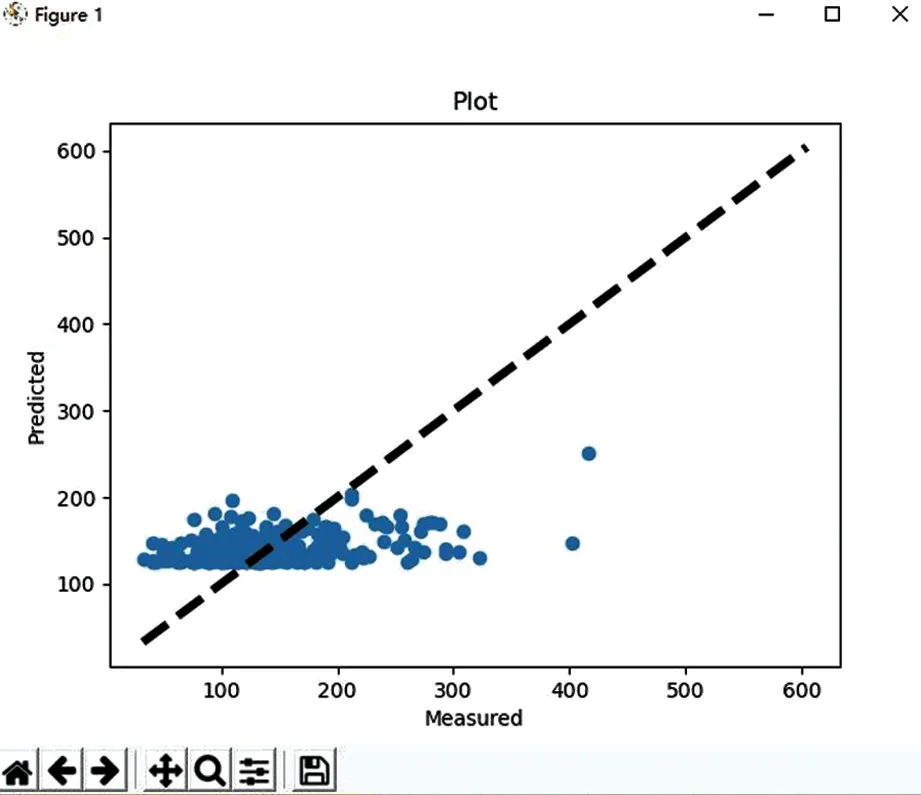
图5 模型在运行时间T2之后结果变化

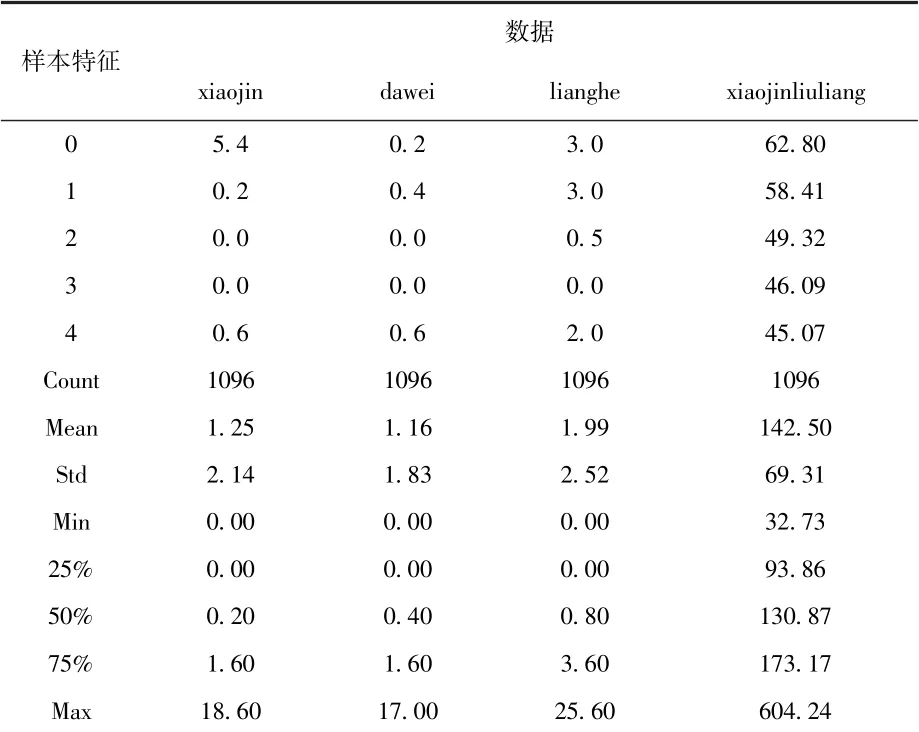
表4 模型运行时间T2数据

(1096，4)

LR.intercept＿:[125.79028717]

LR.coef＿:[[6.13921908 2.48457902 2.91936099]]

RMSE:61.35

在运行时间T2之后，随着采集数据量的不断增多，发现整体数据偏差过大，离散程度较高，RMSE数据有其他影响因素。进行原因分析后针对现有模型中的参数进行了优化，加入了连续下雨量、下雨时间、连续下雨天等参数，进行了模型的进一步细化，离散变化如图6所示，程序优化输出后结果如下:

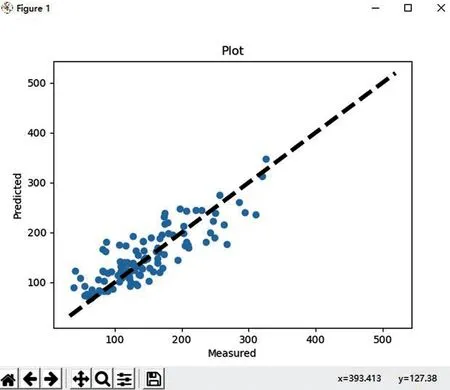
图6 模型参数优化后(在运行时间T2之后结果变化)

LR.intercept＿:[53.75315188]

LR.coef＿:[[0.33490087－0.62412436 2.64343157 1.22031563 1.06905883－1.25737151－0.18086965 1.16870534 0.94289013 1.27620644 0.46292934－2.19127078 1.84307365 1.98384269 0.70598535]]

RMSE:34.96

在运行T3时间之后，模型得到了优化，离散程度更小，如图7所示，程序运行结果如下:

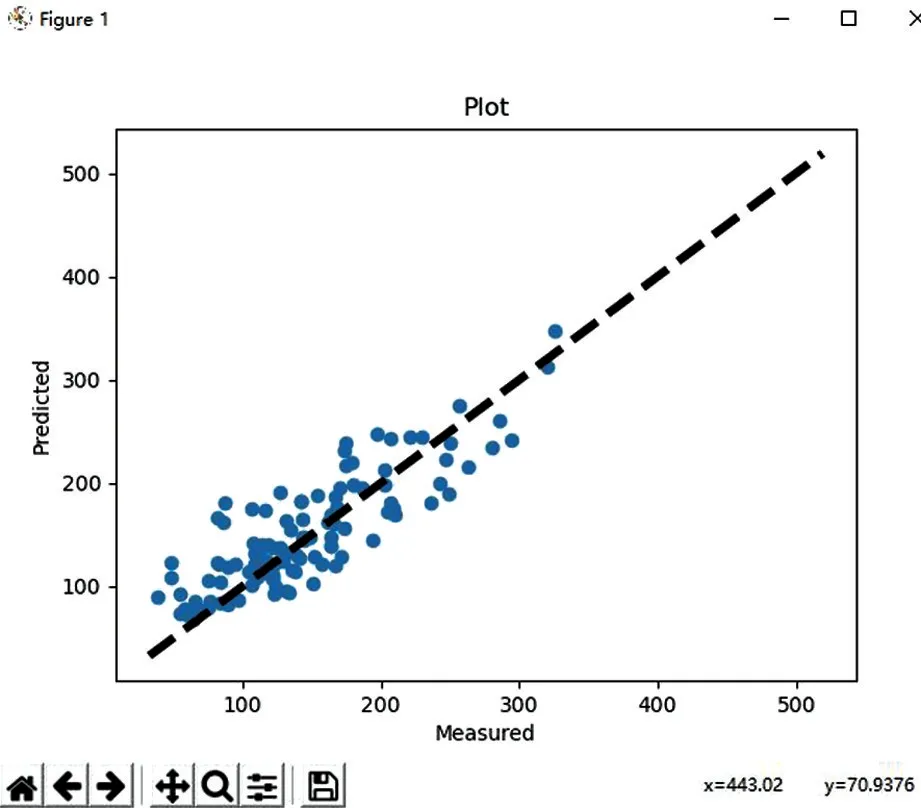
图7 模型在运行时间T3之后结果变化

LR.intercept＿:[53.84795419]

LR.coef＿:[[0.30243946－0.55534329 2.67885757 1.28878908 1.07345404－1.26625626 －0.1710308 1.15262515 0.8902583 1.26158854 0.45054248－2.13878691 1.84879842 1.94619908 0.70365609]]

RMSE:33.25

由此可以看出，随着时间的不断向前推移，该模型对于山洪的预测离散度会逐渐减小，真实值与预测值之间的误差也会越来越小，导致产生误差的原因分析，主要为:

一是山洪的成因机制较为复杂，具有非常明显的非线性特征，山洪形成的影响因素众多，降雨是其中最为重要的变量，其他如地形地质、土壤、植被等因素对于山洪的形成也有一定程度的影响。对于面域较大的水文环境，可能受到上游梯级电站不定期放水影响从而导致数据偏移较大。

二是在机器学习过程中，需要大量数据，由于传感器数量偏少，不能覆盖整个山洪区域，因此，在机器学习中会导致参数偏移较大。随着时间的推进，采集数据量不断增多，机器学习会不断优化和调整参数，尽最大可能性提高数据精度。

三是小金流域上游小水电站影响，缺乏水电站放水量数据导致山洪流量无法修正。

以下是四川省阿坝州龙溪沟利用该模型进行的数据盲测，龙溪乡位于汶川县的最北部，距国道317线3.5km，西与理县桃坪乡相连，东北同茂县接壤，南与克枯乡相邻，全乡幅员面积214.3km2。龙溪沟流域面积187km2，设有龙溪和木扎两个雨量站，上游无梯级电站。利用本洪水预测模型进行数据盲测，最终的程序运行结果如表5所示。

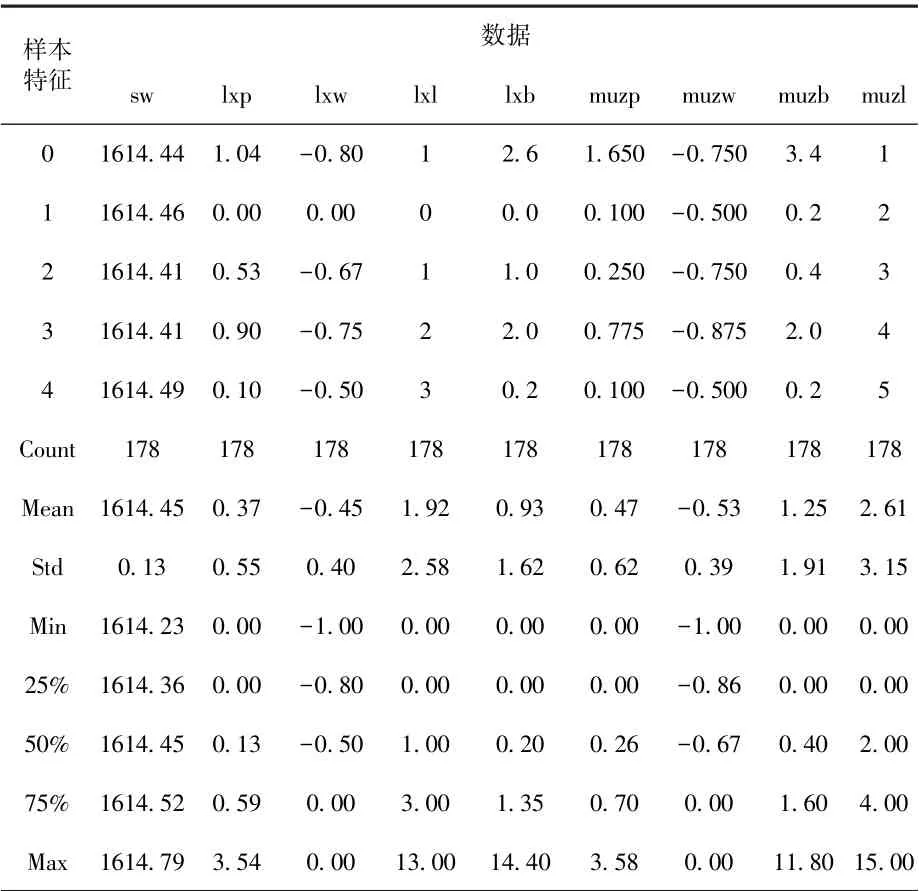
表5 模型盲测数据

LR.intercept＿:[1614.4154718]

LR.coef＿:[[－0.02352098 0.03386048 0.01865036－0.00408701 0.04258365 0.04459187－0.00338166 0.02211623]]

MSE:0.02

RMSE:0.12

由此可以看出，在面域较小，且上游无梯级电站的山区水文环境下，该模型具有较小的离散型，数据的分散程度小。通过模拟盲测，说明该模型具有一定的迁移性。

6 结论与讨论

本文建立的基于机器学习和大数据的山洪预测模型，通过Scikit－Learn(sklearn)机器学习平台对其进行了模拟，模拟有一定的效果，说明该模型适用于小规模山洪的预测，主要结论包括:

(1)山洪的成因机制较为复杂，具有非常明显的非线性特征，山洪形成的影响因素众多，降雨是其中最为重要的变量，其他如地形地质、土壤、植被等因素对于山洪的形成也有一定程度的影响。对于面域较大的水文环境，可能受到上游梯级电站放水影响从而导致数据偏移较大。

(2)对于面域较小的水文环境，由于受到降雨的影响会更大，因此，数据准确度会随着数据量的增多而提高，更适合于小规模部署。

(3)预测值与真实值之间存在一定的误差，但随着时间的逐渐向前推移，RMSE的离散程度在缩小。

本文中所涉及的洪水预测模型经过前期的虚拟仿真和实地盲测，根据模型特性，需要去不断寻找山洪与山洪成因的各种因素之间的联系和影响关系，还需要不断地学习和大量数据的对比计算，因此，采集器的数量和学习时间是一个重要不可或缺的条件，未来还将通过增加传感器类型、增加传感器数量等方式进一步提高计算精度。在算法改进方面，还将引入卷积神经网络，卷积神经网络是将来模型的一个重要方向。