电火花加工放电通道建立过程的电磁场耦合模型

2023-01-04郭建梅贾志新

电加工与模具 2022年6期

郭建梅，何虎，姜浩，王津，贾志新

（1.北京市电加工研究所有限公司，电火花加工技术北京市重点实验室，北京 100191；2.北京科技大学机械工程学院，北京 100083）

电火花加工放电通道的形成机理是电火花加工技术领域的一个重点研究问题。但电火花加工放电时间短、放电空间小，对其观察和测量比较困难。通过计算机仿真技术探究放电通道形成过程是一种有效手段[1-3]。Kunieda等[4]在测量单次脉冲放电的材料去除量时发现，脉宽不相同，阴、阳极的材料去除量比例也不同。Xia等[5]指出，分布于阴极的能量总少于阳极，约80%的能量被阴阳极吸收，而用于去除工件材料的能量只占1%。李晓慧[6]利用多物理场耦合建立了稳态时的放电通道模型，发现放电通道中心轴的压力最大，而最高温度位于通道中心轴的极间中点，同时研究了放电电流和放电间隙对放电通道的影响。武书昆等[7]使用理论和实验的方式证明磁场作用下的放电通道会产生偏移，并计算出电子运动轨迹和放电点的理论偏移值，通过实验证明洛伦兹力改变了放电点的位置，造成工件上放电点的位置变化，进而引起电蚀坑形貌变得大而浅。Liu等[8]基于场致发射理论推导了电火花加工各阶段相互作用和电火花加工能量的分布函数，并进行了通孔加工实验，得到的理论结果与实验数据吻合较好。Somashekhar等[9]基于单脉冲放电和电热理论建立了单脉冲热仿真模型，仿真得到的放电凹坑与实验测量结果相近。Govindan等[10]通过单脉冲放电实验发现，在磁场辅助下，电火花加工的凹坑直径减少、深度增加，材料去除变得更均匀，同时实验还建立分析模型对该结论进行了验证。

电火花加工放电通道中运动的带电粒子的周围会产生磁场，磁场使带电粒子受到洛伦兹力作用而改变运动方向，进而改变电场分布，因此极间电场和磁场互相影响，二者具有耦合关系。然而以往建立的电火花加工极间放电通道模型忽略了电磁场耦合这一关键因素，为此本文针对电火花加工中放电通道等离子体运动沿着电极轴向产生环向磁场的问题，以放电等离子理论和麦克斯韦方程为基础，建立放电通道电场和磁场耦合的物理模型，并基于该模型对电火花加工极间放电通道的直径和电子、离子的稳定时间等进行了仿真研究。

1 电火花加工放电通道模型

1.1 电火花加工放电假设

在电火花加工中，外加电压作用在电极和工件之间，放电通道最可能出现在两极间电场强度最大处。在针-板放电中，针尖处为尖锥型，电势比较密集，最易产生放电，故本文选择针-板放电作为仿真对象、以电极为阴极，既简化对放电通道初始形成位置的判断，又符合实际情况。

电火花加工一般在煤油或者水中进行，但放电通道究竟是直接发生于液体介质中，还是电场先将液体介质气化再在气体介质中形成放电通道，目前对此未有明确的理论依据。本文假设放电通道形成于气体介质中，并且为简化电离过程，假设气体介质为氩气，其密度函数为：

式中：n为氩气的单位体积分子数；p为理想气体系统的压强，Pa；k为波尔曼兹常数；T为理想气体系统的温度，K。

1.2 电火花加工放电通道动态模型

1.2.1 时间空间离散化

本文利用PIC-MCC理论跟踪粒子的运动和碰撞[11]，共定义包括电场强度E、磁场强度B、粒子位置x、速度v、电荷密度ρ与电流密度J在内的6个基本物理量。使用有限差分法对时域进行离散化，为计算放电通道内电磁场，以半个固定长度的迭代进行计算，即某个时刻的电场或磁场是下半个固定长度的磁场或电场的求解初值，交替计算整个单元网格内的电场和磁场；同时，为方便计算和离散需求，设置单元网格边长为dx=dy=dz的正方体网格，而时间离散的固定长度由单元网格的长度决定。

1.2.2 电磁场的计算与更新

本文采用麦克斯韦方程组分析和研究电火花放电通道内的电场和磁场；采用各向同性的氩气作为介质，可构建电磁场与介质特性的关系为：

式中：D为电通密度；ε为介电常数；E为感应电场强度；B为磁感应强度；μ为导磁常数；H为磁场强度；J为电流密度；σe为电导率；Ji为外加电流密度；M为磁流密度；σm为磁导率；Mi为外加磁流密度。

对于电磁场的计算，为使问题简化，只需计算麦克斯韦两个旋度方程即可实现电磁场耦合的迭代更新。

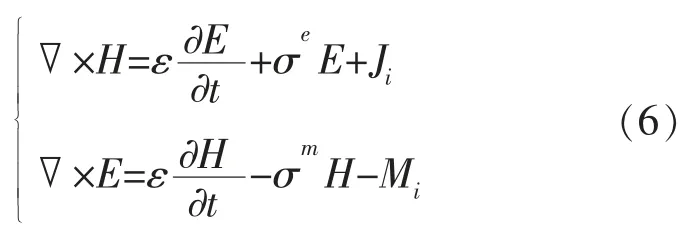
使用YEE元胞法的时域有限差分法对式（6）进行离散，即可得到电磁场耦合的迭代更新。

1.2.3 粒子运动计算与更新

在仿真过程中，每一次迭代运算时，通道内的带电粒子会在电磁场作用下运动到其他位置。粒子在磁场作用下的运动状态满足Newton-Lorentz力方程[12]。在强电场作用下，质量非常小的电子会被加速到接近光速，故需采用相对运动来处理粒子的运动情况。定义相对运动因子γ，则相对运动条件下的修正磁场Bu=γB，由此可得到采用相对运动处理的Newton-Lorentz力方程的差分方程形式为：

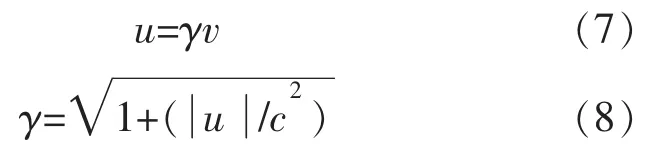
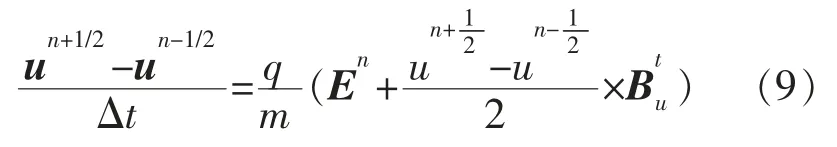
式中：u为粒子相对运动下的速度；v为粒子速度；c为光速；m为粒子的质量；q为粒子的电荷量。

2 放电通道仿真结果及分析

2.1 仿真结果及其实验验证

2.1.1 仿真结果

本文选择的时间步长Δt为1E-13 s。其他部分参数见表1，仿真流程见图1。使用Matlab软件进行编程，通过有限次的迭代可使整个电火花加工单脉冲放电的内部物理过程可视化，从而得到放电通道随着时间变化的过程图。

表1 Matlab仿真参数的设定

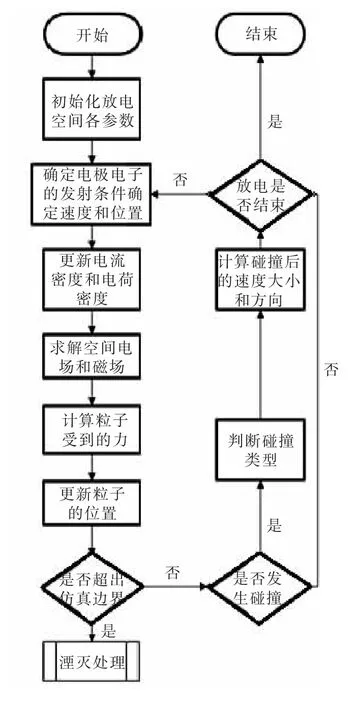
图1 仿真流程图

图2 是在仿真参数开路电压为120 V时仿真计算得到的放电通道过程变化图。其中X、Y、Z轴分别代表所建模型中的各个方向。针尖（阴极）位于YZ平面，金属平板（阳极）平行于YZ平面，距离YZ平面15E-6 m。

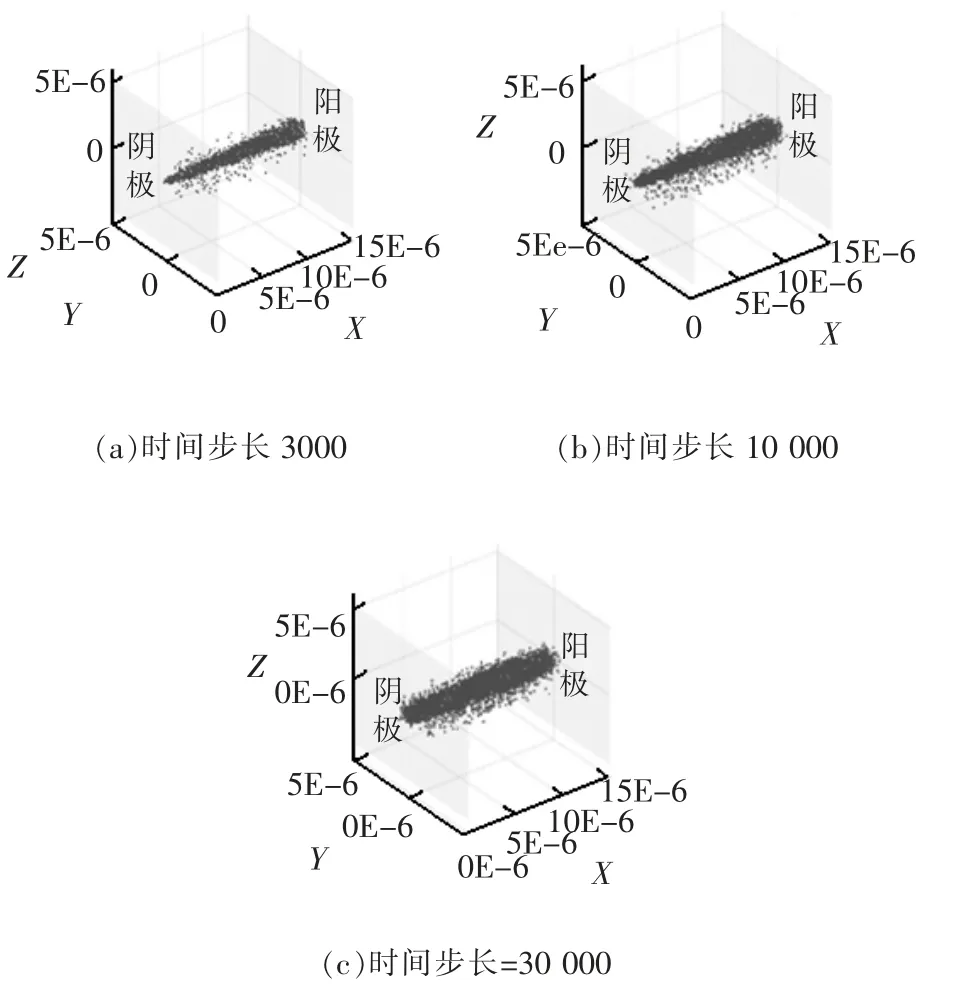
图2 放电通道建立过程仿真结果

在电火花放电通道形成的过程中，一开始通道内出现少量带电粒子，通道形状为细小锥形，而电子在加速运动过程中和通道内介质发生碰撞，使其在通道内的电子运动方向发生偏转，并且电离碰撞产生的新的电子运动方向具有不确定性，导致通道内电子散射，进而使放电通道急剧扩张。

2.1.2 放电通道形成时间实验验证

在电火花加工放电通道形成过程中，等离子的运动主要是电子在运动，但是由于离子的质量远大于电子的质量，离子运动很慢。随着大量带电粒子产生，电子加速通过放电通道到达阳极，离子则被滞留在放电通道内并形成了不稳定的放电通道。随着时间推进，阳极附近的离子通过缓慢的加速运动到达阴极，则此时整个通道内的粒子都处于平衡状态。因此，可认为放电通道形成的标志为放电通道内的等离子体处于平衡状态，即通道内的粒子数量不再发生改变。

从图3所示仿真结果可见，在放电通道形成初期的极短时间内（约66e-13 s），电子的数量急剧增加并迅速达到平衡状态，而通道内的离子数量缓慢增加并大约在2 ns之后趋于平衡状态。当通道内的电子和离子的产生速率不再变化时，放电通道就已经形成了。

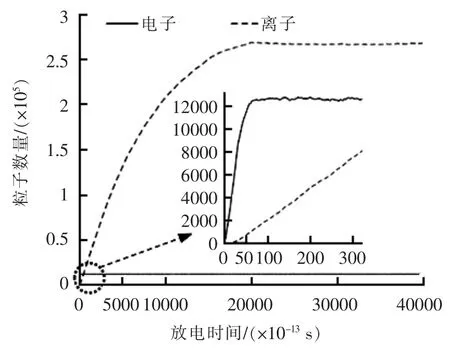
图3 放电通道内电子和离子数量变化图

2.2 磁场对放电通道的影响

高速运动的带电粒子会产生电磁场，并反过来对放电通道内的带电粒子产生一定影响。图4是忽略磁场影响和考虑电磁场耦合的放电通道直径仿真结果。可见，无磁场作用下的放电通道直径始终比有磁场作用下的放电通道要大。原因在于，带电粒子在磁场下受洛伦兹力影响，运动速度偏向放电通道中心，使放电通道直径减小，这也意味着磁场使放电通道的能量密度增大。

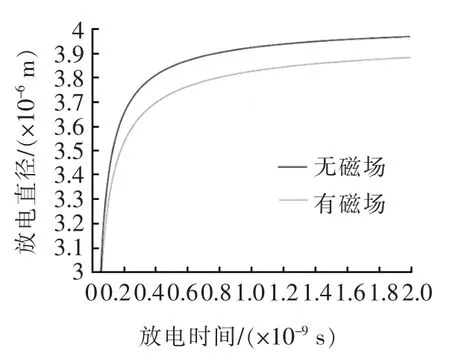
图4 电火花加工磁场对对放电通道直径的影响

2.3 电压对放电通道的影响

图5 是电压对放电通道电子和离子数量达到稳定所经历时间的影响。可见，随着电压的增加，电子和离子数量达到稳定状态所经历时间减少，原因是电压的升高使极间电场强度增大，电子和离子运动加速度增大，能较快到达电极表面。电子和离子达到稳定时所经历时间都是极短的，通常电子所需时间约为4.8e-3 ns至7.6e-3 ns，离子所需时间约为1.5～2.5 ns。仿真结果说明，在常用的电火花加工电压条件下，只要具备击穿条件，放电通道的建立时间是极短的。这也给电火花加工脉宽的最小值提供了依据，随着加工精度的不断提高，已出现关于纳秒脉宽电火花加工的研究，但当脉宽小于建立放电通道所需时间后，就难以发生火花放电。