基于长短时记忆神经网络（LSTM）的钟差预报算法

王 锐，弓剑军，杜洪强，武文俊，3

（1.中国科学院国家授时中心，西安 710600；2.中国科学院大学，北京 100049；3.中国科学院大学天文与空间科学学院，北京 100049）

1 引 言

当前，国际标准时间是原子时和世界时以闰秒方式形成的协调世界时。 原子时由一组原子钟利用原子时算法计算得到，并产生连续稳定的时间信号。 原子钟钟差预报在原子时算法中是必不可少的环节，主要表现在两个方面：1）在对原子时进行计算时，若原子钟组的数量以及原子钟的权重改变时，则会引起频率和相位的跳变，为了保证时间尺度频率和相位的连续性，必须通过原子钟预报进行修正；2）对主钟系统的相位微调仪进行频率驾驭时，需要通过钟差预报算法基于原子钟过去的频率偏移量来预报当前的频偏量，由此计算驾驭量［1，2］。 因此，原子钟钟差预报对于原子钟守时应用至关重要［3］。

目前，用于钟差预报的常用算法主要包括线性多项式模型、灰色模型和Kalman 滤波模型等。 线性多项式模型对异常值较为敏感，会因某些异常值而影响预报结果［4］；灰色模型只适用于中短期的预测和指数增长的预测［5］；Kalman 滤波模型在非线性的过程中达不到最优的估计效果［6，7］。 通常根据原子钟钟差数据特性来选择预报模型，但随着原子钟长期噪声造成的内部不稳定性，多数预报算法的预报精度随着预报时间的增加而下降。

近年来，在卫星导航领域中利用长短时记忆神经网络（long short⁃Term Memory，LSTM）算法进行卫星钟钟差预报，并优化了卫星导航精度［8，9］。LSTM 可以有效地在长时间序列中传递和表达信息，并且选择记忆长时间前有用的信息和忽略无用的信息，因此能够改善原子钟长期内部噪声以及原子钟的长期漂移造成的影响［10，11］。 原子钟长期预报水平的改善有助于提升以月为计算间隔的独立原子时的性能。 基于LSTM 预报模型对守时型原子钟进行原子钟钟差预报，并与常用预报模型进行对比验证。

2 LSTM 原理及其应用

2.1 LSTM 原理

LSTM 是一种循环神经网络（RNN），用于建模长序列数据之间的上下文依赖关系，LSTM 还可以记住预测之间的网络状态，因此适用于解决长期噪声的钟差数据［12］。 LSTM 是一种递归神经网络，在当前t时刻会将t－1 时刻的数据信息作为输入，因此在计算当前时间的内容时包含了之前所有时间段累积的数据信息。 LSTM 递归神经网络结构如图1 所示。

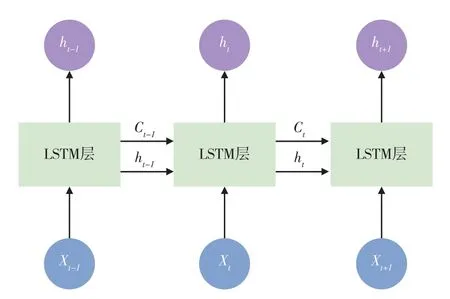
图1 LSTM 递归神经网络结构图Fig.1 Structure diagram of LSTM recurrent neural network

由图1 可知，LSTM 网络结构由序列输入层和LSTM 层构成。 序列输入层负责将时间序列数据分割并输入神经网络单元，包括当前t时刻的时间序列数据信息Xt和前t－1 时刻预测当前t时刻的数据状态ht－1；LSTM 层负责学习时间序列数据段之间的长期依赖关系，计算下一时刻t＋1 的预测值和数据状态ht。 LSTM 层利用门机制控制数据信息传递的路径，判断数据信息的流通和损失，LSTM 层单元结构图如图2 所示。

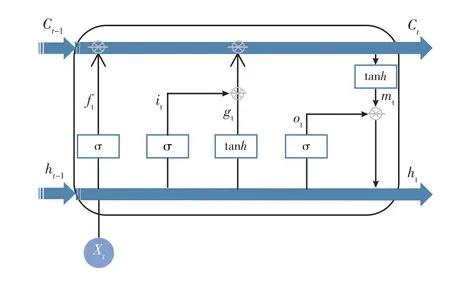
图2 LSTM 层单元结构图Fig.2 Structure diagram of LSTM layer cell

由图2 可知，LSTM 层设计了一个神经网络记忆细胞，具备选择性记忆的功能，可以自由选择记忆每个时间段里面的重要信息，过滤掉噪声信息，减轻记忆负担，由权值、偏置以及激活函数组成。其中C是控制参数，决定保留和遗忘的信息。σ函数是LSTM 最常用的激活函数，输出0 到1 之间的数值，描述每个部分有多少量可以通过，0 代表不需任何量通过，1 代表允许全部量通过。 各个函数层之间采用“门”机制的方式控制数据流通，每个神经网络记忆细胞包含3 个“门”，分别如下：

1）遗忘门（forget gate）ft：负责遗忘前面时间的状态信息，即Ct－1的哪些特征被用于计算Ct。 决定了上一步的记忆在这一步保留的比例。 数据元素取值范围为［0，1］，1 代表我们保留之前记住的信息，0 代表我们不用记住前面的信息。ft的计算公式如下：

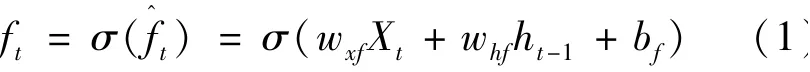
式中：σ——遗忘门的激活函数；Xt——时间序列数据信息；ht－1——前t－1 时刻预测当前t时刻的数据状态信息；wxf——Xt的权值；whf——ht－1的权值；bf——遗忘门的偏置项。

2）输入门（input gate）it：负责筛选新的记忆，去掉无用的新的记忆（输入）信息，产生控制信息。it的计算公式如下：

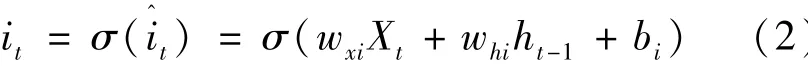
式中：wxi——Xt的权值；whi——ht－1的权值；bi——输入门的偏置项。

此外，gt的计算公式如下：

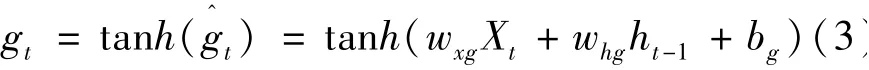
式中：gt——单元状态更新值，产生候选数据信息；tanh——单元状态激活函数；wxg——Xt的权值；whg——ht－1的权值；bg——单元状态偏置项。

因此，gt和it结合可得到候选数据所需要保留的数据信息，结合上一个时间段所保留的数据信息，两部分相加得到最终的当前时刻的数据控制信息为：

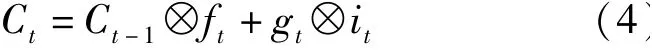
式中：Ct——当前t时刻的控制参数；Ct－1——前t－1时刻的控制参数。

3）输出门（output gate）ot：根据新旧记忆结合的全部记忆进行转化成为实际所需要的信息，由输入数据Xt和隐藏节点ht－1与其对应权值wxo和who经过σ函数激活计算为：

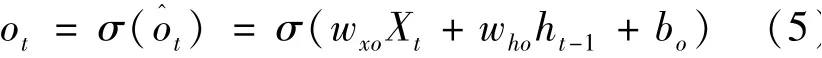
式中：wxo——Xt的权值；who——ht－1的权值；bo——输出门的偏置项。

最后，为了计算预测值y＾t并生成下个时间段完整的输入，需要计算隐藏节点的输出ht，隐藏节点由输出门的控制记忆信息与当前时刻全部数据信息相结合计算得到：

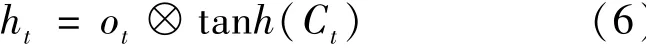
当传递信息到下一时刻，除了将长期信息的状态传递到下一时刻，也会将当前时刻的输出作为近期信息传递到下一时刻。 所以预测值y＾t由输出的隐藏节点与其对应权值wyh相乘得到：

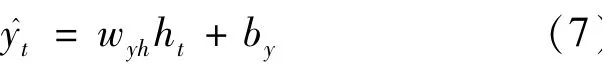
2.2 LSTM 原子钟模型构建

建立LSTM 原子钟钟差预报模型共分为以下五步：第一步进行原子钟钟差数据预处理，将钟差数据的异常值剔除并进行二次差分处理，可使得数据平稳并降低LSTM 网络的复杂程度；第二步将数据进行分割，确定时间步长和数据输入特征并定义LSTM 网络结构；第三步将数据归一化并编译LSTM网络，确定激活函数；第四步优化并确定训练模型参数；第五步设置目标函数评估预报模型并输出预报结果［9，12］。 LSTM 原子钟模型构建流程图如图3所示。

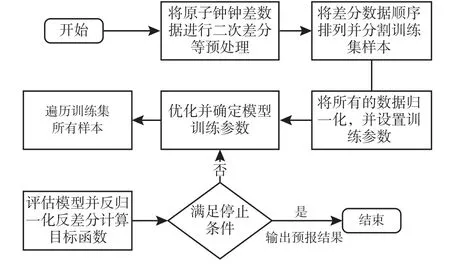
图3 LSTM 原子钟模型构建流程图Fig.3 Flow chart of building the atomic clock model of LSTM

1）数据预处理：除常规异常值剔除及相跳、频跳的插值数据处理外，还需将钟差数据进行二次差分处理，可以保证数据的平稳性，并且能够提高预报精度；

2）数据分割：按照交叉验证法将数据划分为训练样本集和验证集，将数据集D按照时间分割成k个大小相同的数据子集，每个子集Di都尽可能保持数据分布的一致性。 根据前一时间段作为输入变量，下一时间段作为输出变量，将这个时间序列数据集重构为一个监督学习问题；

3）数据归一化：将分割后的训练集合验证集均进行归一化，可以帮助网络模型更快的拟合。 设置LSTM 训练学习损失率、隐藏层神经元数、批次大小以及迭代次数，并设置防止过拟合或欠拟合的监视变量；

4）模型训练：为了快速找到最优参数，选用小批量随机梯度下降算法进行模型的参数优化，将分割后的训练样本集按照设置的参数（训练学习损失率为10－6、隐藏层神经元数为200、批次大小为30×15、迭代次数为128）进行LSTM 训练，训练优化器采用自适应优化算法中的Adam 算法，并将模型训练结果作为预报值输出；

5）预报评估：对模型训练结果进行反归一化和反二次差分处理，得到原始的钟差数据，并与验证集进行对比评估。

3 实验结果及分析

实验以国家授时中心型号为VH085、VH340氢钟数据和型号为Cs3436、TA3050 铯钟数据为参考，选用日期分别为2020 年10 月1 日至2021 年6月30 日，以及2021 年4 月1 日至2021 年9 月10日的钟差数据，实验数据采样间隔均为1 h，预报时间长度分别为72 h，240 h 和720 h，分别采用线性多项式模型、灰色模型、kalman 模型和LSTM 模型进行预报，并将预测差值进行比较，如图4 至图7所示。

由图4 可知，VH340 在72 h 预报时长，线性多项式模型的预报精度优于其他模型，在240 h 和720 h预报时长，LSTM 预报模型的预报误差均小于其他模型。

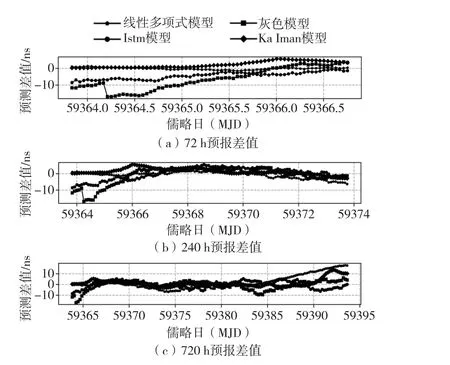
图4 VH340 预报误差图Fig.4 Forecast error graph of VH340

由图5 可知，VH085 在72 h 预报时长，灰色模型的预报精度优于其他模型，在240 h 和720 h 预报时长，LSTM 预报模型的预报准确度相对于其他模型更高。

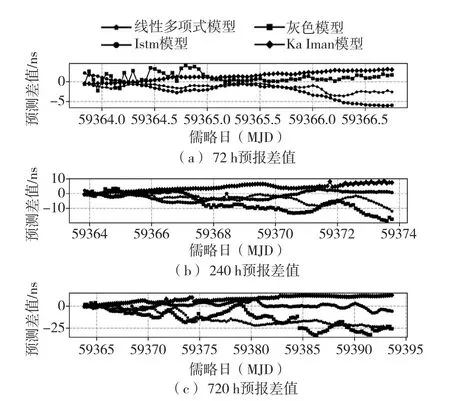
图5 VH085 预报误差图Fig.5 Forecast error graph of VH085

由图6 可知，Cs3436 在72 h 和240 h 预报时长，kalman 模型的预报精度优于其他模型，在720 h预报时长，LSTM 预报模型的预报误差相对于其他模型都小。

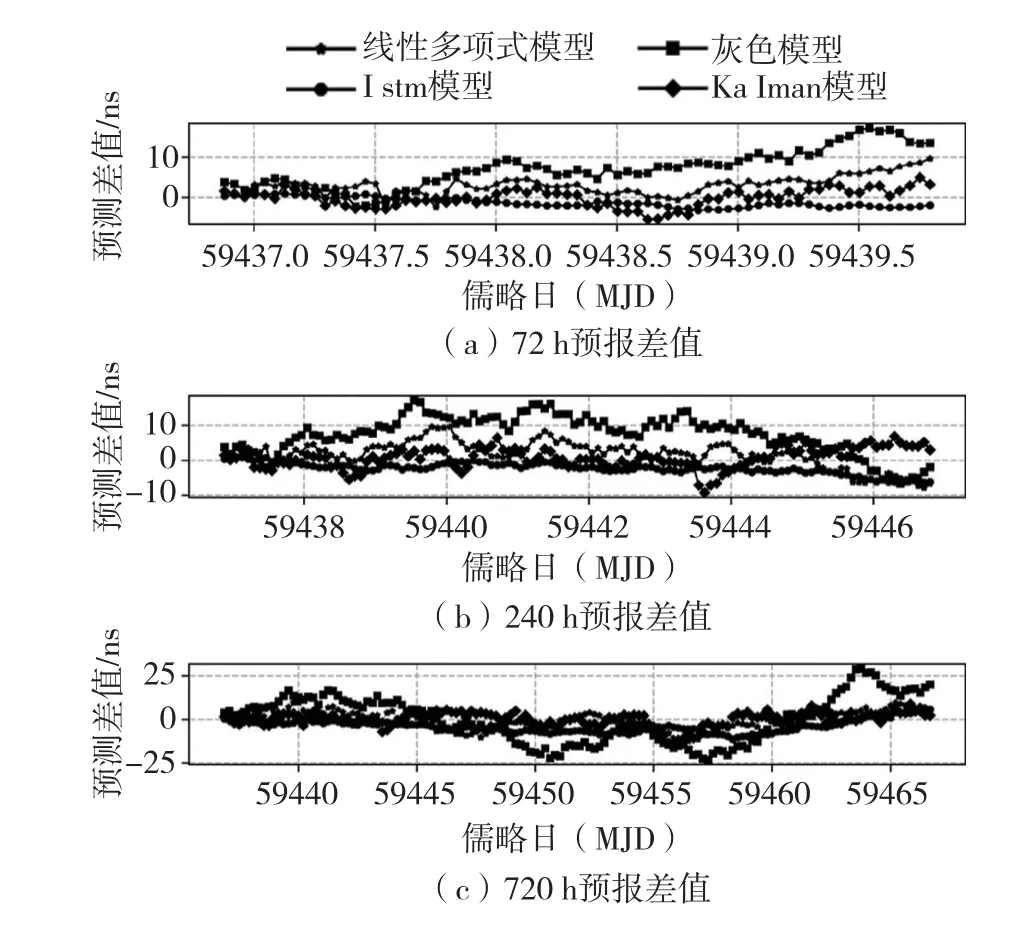
图6 Cs3436 预报误差图Fig.6 Forecast error graph of Cs3436

由图7 可知，TA3050 在72 h 预报时长，灰色模型的预报精度优于其他模型，在240 h 和720 h 预报时长，LSTM 预报模型的预报准确度相较于其他模型更高。

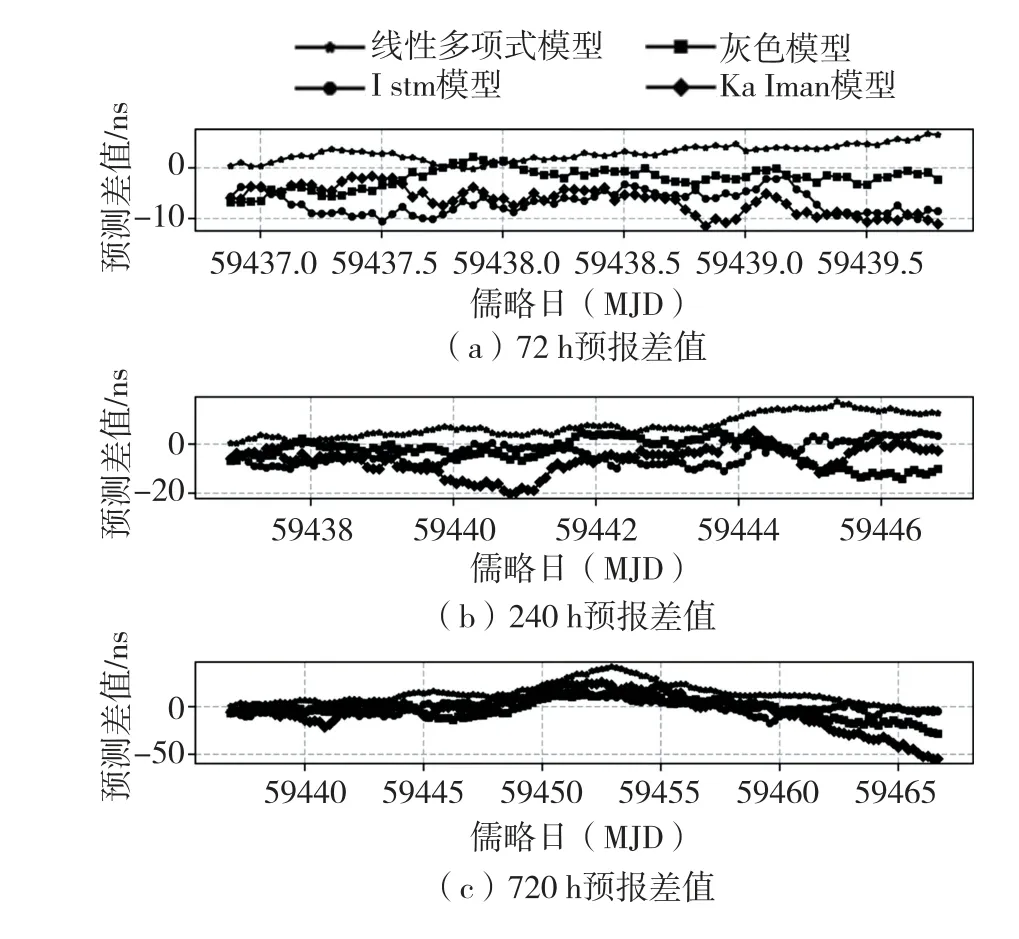
图7 TA3050 预报误差图Fig.7 Forecast error graph of TA3050

最后，采用均方根误差（root mean squared error，RMSE）来评估预报算法的性能［13］。 RMSE 的具体定义为：

由表1 可知，线性多项式模型、灰色模型和Kalman 模型随着预报时长的增加，预报误差明显增加，在短期预报时长中，线性多项式模型和kalman模型预报精确度比较稳定且可靠；在中长期预报时长中，LSTM 相较其余预报模型的预报精度有显著的提升。

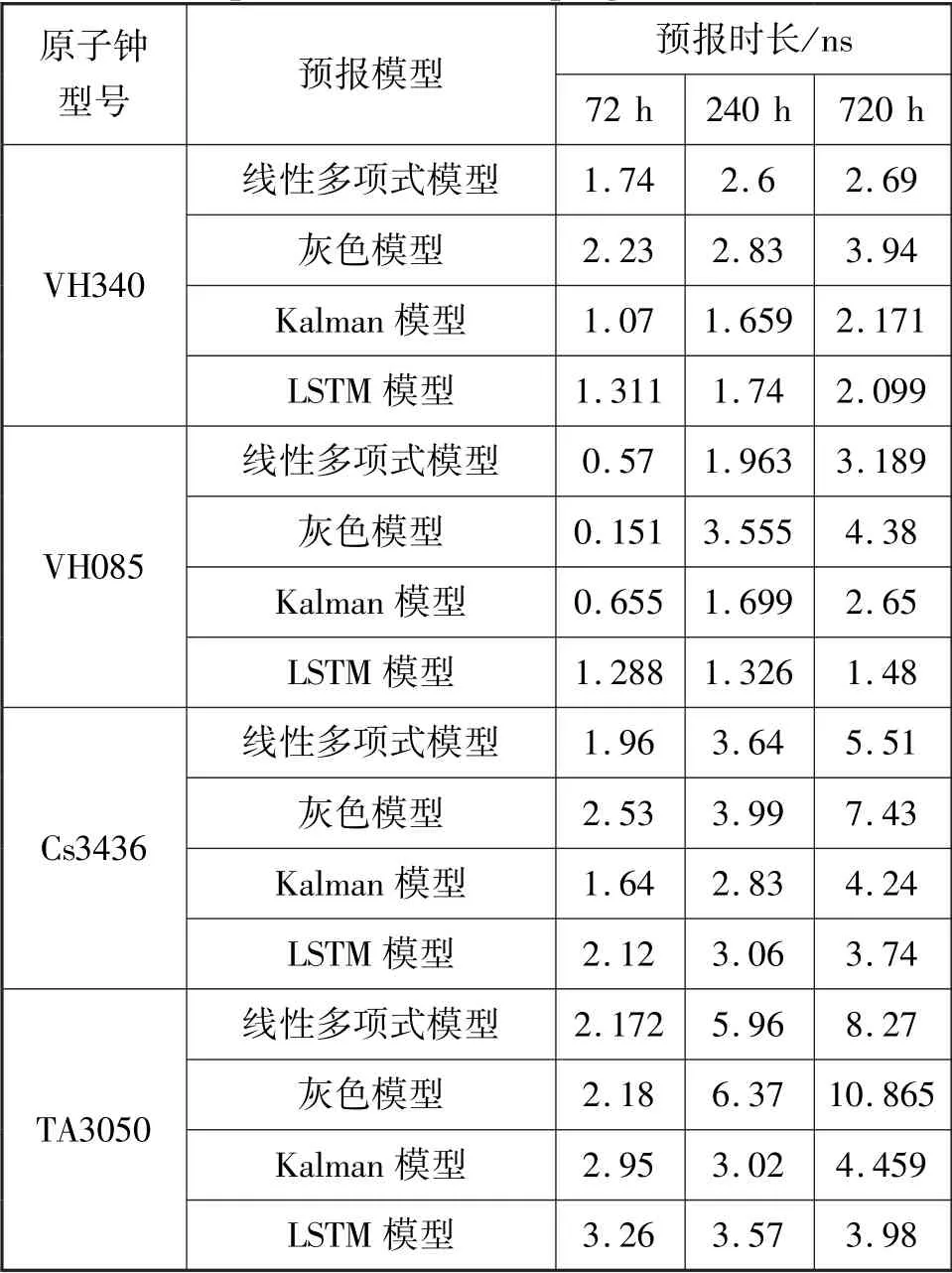
表1 预报模型RMSE 对比表Tab.1 Comparison table of the prognostic model RMSE

通过以上对比可看出，线性多项式模型具有误差的累积效应，在240 h 预报时长，四台原子钟钟平均累积误差增大25.8 %，在720 h 预报时长，平均累积误差增大68.2 %。 灰色模型利用灰色数学处理不确定量，使之量化寻找数据运行规律，没有考虑原子钟内部噪声影响，在240 h 预报时长，四台原子钟钟平均累积误差增大17.9 %，在720 h 预报时长，平均累积误差增大74.5 %。 Kalman 模型经过多次状态估计迭代去除原子钟内部大部分噪声影响，预报精度更加可靠，在240 h 预报时长，四台原子钟钟平均累积误差增大22.3 %，在720 h 预报时长，平均累积误差增大37.8 %。 而LSTM 具有较高的模型复杂度以及高度的非线性关系处理，拟合效果更优，根据长序列数据之间的上下文依赖关系，可以降低原子钟内部噪声造成的误差影响，利用预测之间的网络状态，使得LSTM 对钟差异常值数据不敏感。 在240 h 预报时长，四原子钟钟平均累积误差增大28.9 %，在720 h 预报时长，平均累积误差增大32.7 %。因此，LSTM 模型在240 h 以上的原子钟钟差预报可以实现更高的预报精度。

LSTM 对数据量依赖较大，而短期的原子钟钟差数据的依赖关系较弱，因此LSTM 模型不适用于短期钟差数据的预报。 LSTM 在训练过程中采用串行数据运算，对处理器等硬件的性能要求较高。 因此，在利用LSTM 模型训练数据时，要使用GPU 并加大计算机的硬件存储带宽，可以使用更多的计算单元加快训练速度。 此外，在数据预处理阶段要循环多次剔除异常值等脏数据，避免LSTM 模型训练数据过程中过度的拟合训练集中的特有特征，导致预报准确度降低。

4 结束语

针对传统钟差预报模型长期预报精度快速下降的问题，提出了一种采用小批量梯度下降法构建LSTM 钟 差 预 报 的 模 型， 并 以VH085， VH340，Cs3436 和TA3050 钟差数据为样本，实现了原子钟LSTM 钟差实际预报，最后将LSTM 钟差预报结果分别与其他三类原子钟钟差预报模型进行预报误差对比。 预报结果表明：LSTM 神经网络模型参数选择小批量随机梯度下降算法进行优化，可以在参数空间快速找到最优组合，并使得LSTM 网络模型实现更好的拟合。 在72 h 的预报时长，LSTM 预报精度比其他三类模型较低；在240 h 的预报时长，LSTM 与其他三类模型预报效果各有优劣；在720 h 的预报时长，LSTM 预报性能明显优于其他3 类模型。