基于改进变分模态分解和信息融合的故障选线
2023-01-04林立成黎静华
兰 飞,林立成,黎静华
(广西电力系统最优化与节能技术重点实验室(广西大学),广西 南宁 530004)
配网故障中,单相接地故障占比80%以上,为提高供电可靠性,中低压配电网通常采用小电流接地系统,这种接地方式可以为故障选线和隔离提供2 h的持续运行时间.但由于单相接地故障特征不明显,导致故障选线的准确率不高.因此,如何在微弱的接地信号中快速、准确地提取故障特征信息是小电流接地系统单相接地故障选线亟需解决的难题[1].
目前现有的小电流接地系统故障选线方法可大致分为3类,第一类为注入法[2-4],它向配电网注入不同频率的信号,通过检测注入信号的变化以实现故障选线,该方法需加设额外的信号注入设备,成本较高,对电网可能会产生不确定的影响;第二类为稳态法[5-7],由于谐振接地系统消弧线圈的过补偿作用,导致健全线路和故障线路的稳态故障电流极性一致,失去了故障特征,使得稳态法发展受限;第三类为暂态法,暂态过程包含丰富的故障特征,受系统运行方式影响小,故障电流幅值大且灵敏度高,因此暂态法得到了广泛应用.文献[8]利用小波变换分解暂态电流,提取故障特征作为极限学习机的输入,成功将机器学习技术运用到配电网的故障选线与定位.文献[9]运用离散小波变换对暂态信号进行小波多分辨率分析,提出一种利用输电线路两端的电流进行故障分类的算法.文献[10]利用小波包变换分解母线差动电流和模型电压得到高频和低频分量,通过判断高频和低频分量的故障特征实现故障分类和故障区段识别.文献[11]利用小波包变换计算出能量比、阻抗因子和能量熵三个特征参数,结合贝叶斯分类器实现故障选线和定位.小波变换对暂态信号故障特征有很好的检测和提取能力,然而最佳小波基函数的选取具有主观性,缺乏完备理论支撑,算法的自适应性不高.随着希尔伯特黄变换(Hilbert-Huang Transform,HHT)的提出,经验模态分解(Empirical Mode Decomposition,EMD)作为其核心,被应用到故障选线中[12-13].EMD不需要预先选取基函数,是一种自适应的信号分解方法,但EMD存在模态混叠和端点效应的缺点.为了克服EMD的缺点,EEMD[14]、CEEMD[15]等改进算法逐渐被提出,通过附加不同噪声的方法,优化了模态混叠问题,但是仍存在信号分解不理想、噪声残留等问题.文献[16]将经验小波变换用作故障检测,经验小波变换结合了EMD和小波变换的优点,避免了端点效应和模态混叠现象,但仍存在选取小波基函数的缺陷.
为了解决上述问题,Dragomiretskiy等提出了变分模态分解(Variational Mode Decomposition,VMD).它有效抑制了模态混叠及端点效应,能将信号自适应分解成若干个本征模态函数(Intrinsic Mode Function,IMF).文献[17]利用VMD和Teager-Kaiser能量算子实现配电网高阻接地故障检测.文献[18]采用VMD和FFT算法分解暂态零序电流信号,得到暂态非工频信号,并结合K-means聚类实现故障选线.虽然以上文献的方法均能实现故障选线,但是都使用了单一选线判据,单一的判据存在可靠性不高的问题,容易导致误判.文献[19]采用VMD对暂态零序电流信号进行“两步走”分解,并基于直流分量的模态能量测度与高频振荡分量的一阶差分测度构造双重判据实现故障选线.然而当故障初始角为90°时,直流分量最小,可能会导致误判,而且VMD的参数选取存在不足,不利于信号的有效分解.
针对上述问题,本文提出参数寻优变分模态分解和信息融合的故障选线方法.该方法以样本熵作为适应度函数,利用自适应权重的粒子群优化算法(Partical Swarm Optimization,PSO)对变分模态分解进行参数寻优,以期达到更好分解效果.通过融合综合相关系数和相对能量系数两种判据,构造具有更高可靠性的综合选线判据.针对母线故障时,仅凭综合相关系数阈值来区分母线故障和线路故障存在主观性的问题,在综合相关系数基础上提出了工频分量极性比较法的辅助选线方法.
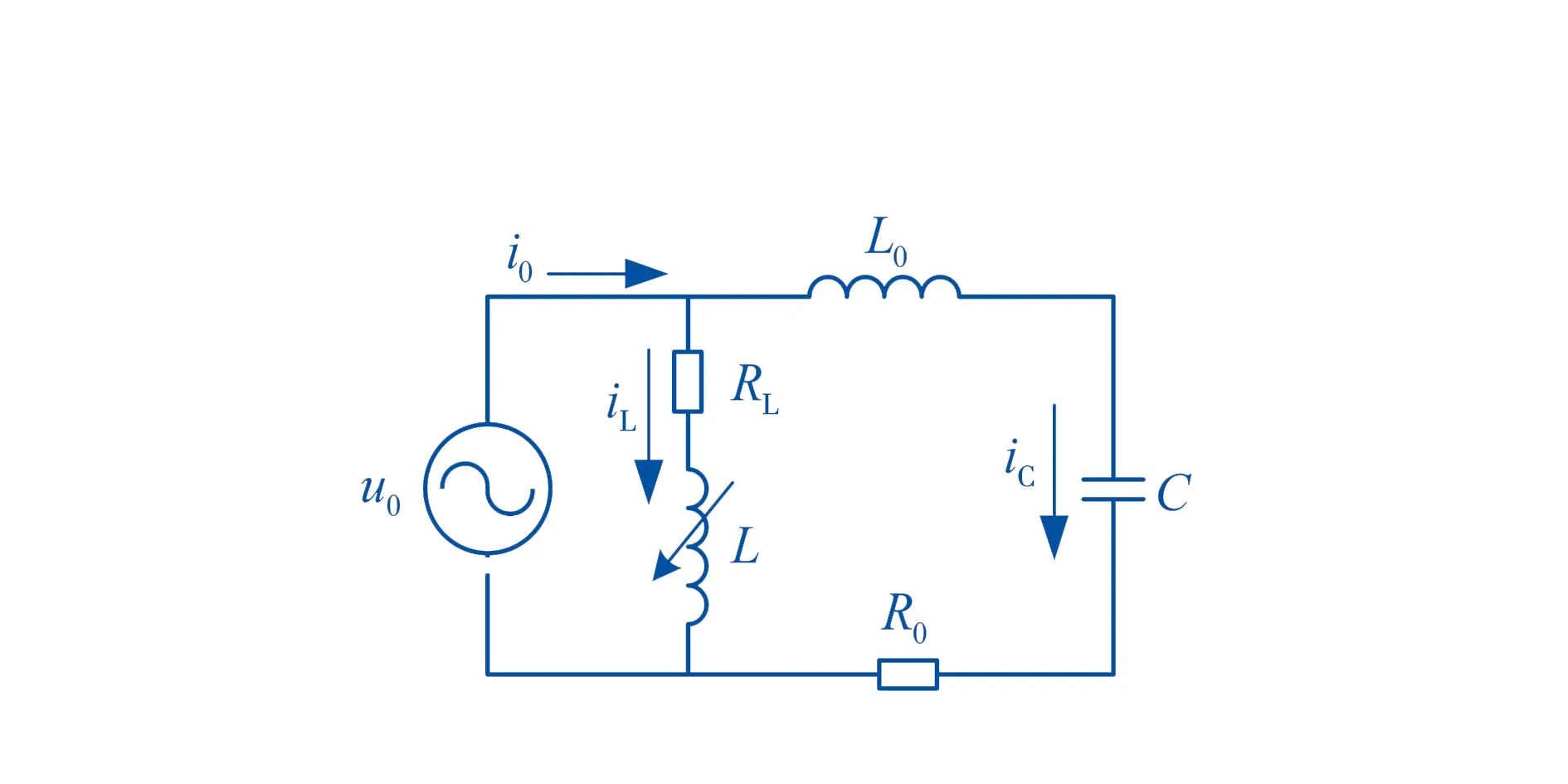
图1 暂态等值电路
1 谐振接地系统单相接地故障特征
中性点经消弧线圈接地系统发生单相接地故障的暂态等值电路如图1所示,u0为零序电源电压,RL和L分别为消弧线圈的有功损耗电阻和电感,R0和L0分别为零序回路的等效电阻和等值电感,C为三相对地等效电容,故障线路的暂态零序电流i0包含了暂态电感电流iL和暂态电容电流iC两部分.
根据图1建立微分方程:
(1)
可以解得故障暂态零序电流
(2)
(3)
公式中:ω为工频;ωf为暂态电容电流自由振荡的角频率;φ为故障的初始角;τC、τL为电容和电感电流的时间常数;ICm、ILm为电容和电感电流的幅值.
由公式(2)和公式(3)所示,当发生单相接地故障时,暂态零序电流i0由衰减直流分量、工频交流分量和高频振荡分量组成.当φ=0°时,衰减直流分量最大,当φ=90°时,衰减直流分量最小.
故障线路的暂态零序电流是由非故障线路暂态电容电流和消弧线圈暂态电感电流叠加而成,iC的高频振荡分量和iL的直流分量频率相差较大,两者无法互相补偿.所以,暂态零序电流的主要特征由暂态电容电流决定,并且在特征频带上,故障线路暂态零序电流幅值最大,故障线路与非故障线路的暂态零序电流极性相反,母线故障时各线路极性相同.
2 基于改进变分模态分解的故障特征提取
2.1 变分模态分解
VMD算法是一种自适应、完全非递归的混合信号分离方法,核心思想是求解约束性变分问题.分解时是通过迭代搜寻变分模型最优解来确定每个模态分量的频率中心和带宽,从而能够自适应地实现信号的频域剖分及各模态分量的有效分离.相较于EMD,VMD具有较强的鲁棒性,能够有效避免模态混叠现象,分解的模态分量更加平滑.
算法原理是在预设分解层数K的情况下,将输入信号分解成K个IMF分量,同时使得各模态的估计带宽之和最小,约束条件为所有模态之和与原始信号相等,VMD算法的表达式如公式(4)所示[20].
(4)
公式中:K为分解层数,{uk}、{ωk}分别对应分解后第k个模态分量和中心频率,δ(t)为单位冲激函数.
为求解上式最优解,引入惩罚因子α和拉格朗日乘法算子λ,将约束变分问题转变为非约束变分问题,得到公式(5)所示的增广拉格朗日函数表达式.
(5)

(6)
(7)
(8)

根据收敛条件ε,判断算法迭代的收敛性,即
(9)
2.2 基于参数寻优的改进变分模态分解
VMD算法最重要的两个参数为分解层数K和惩罚因子α.若K值预设过小,则会使输入信号无法完全分离,导致多个模态并存在同一IMF分量中,反之则会导致过分解.惩罚因子α会影响频带的宽窄,惩罚因子α越小,得到的模态分量带宽越大;惩罚因子α越大,所得模态分量的带宽越小,因此参数的确定尤为重要.
2.2.1 分解层数的确定
根据接地故障特征分析,暂态零序电流由衰减直流分量、工频交流分量和高频振荡分量组成.为了将暂态零序电流有效分解为3个分量,本文参考文献[19]的“两步走”分解法,分解示意图如图2所示.
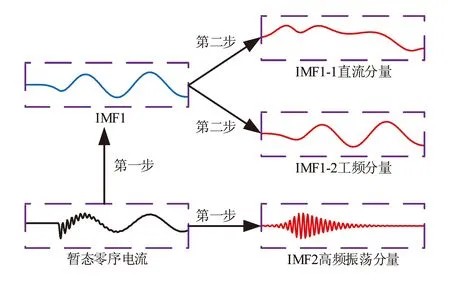
图2 分解层数示意图
首先对信号进行2层分解得到IMF1和IMF2.再对分解结果的IMF1进行2层分解,得到IMF1-1直流分量和IMF1-2工频交流分量,而IMF2对应高频振荡分量.这样执行原因在于直流分量与工频交流分量的频率差较小,工频交流分量与高频振荡分量频率差较大.两步分解法能确保直流分量和工频交流分量在首次分解中可靠地分解到IMF1中,第二次分解也能将直流分量和工频交流分量从IMF1中成功分离.
2.2.2 惩罚因子的寻优
本文利用自适应权重的改进PSO算法[21]来寻优VMD的惩罚因子α,从而得到参数寻优的改进变分模态分解(Optimal Variational Mode Decomposition,OVMD).改进的PSO算法有良好的寻优能力,易于工程实现,是应用广泛的寻优算法.在PSO算法中,每个粒子有相应的速度和位置,粒子的位置代表待优化问题的潜在最优解,通过不断迭代找到全局最优解.
预设惩罚因子α的初始值为100,α的搜索范围为[100,8 000].改进的PSO算法的参数设置如下:学习因子c1=c2=1.496 18,最大惯性权重取0.9,最小惯性权重取0.6,种群规模为20,最大迭代次数为50.利用改进PSO算法寻优VMD的惩罚因子α的流程图如图3所示.
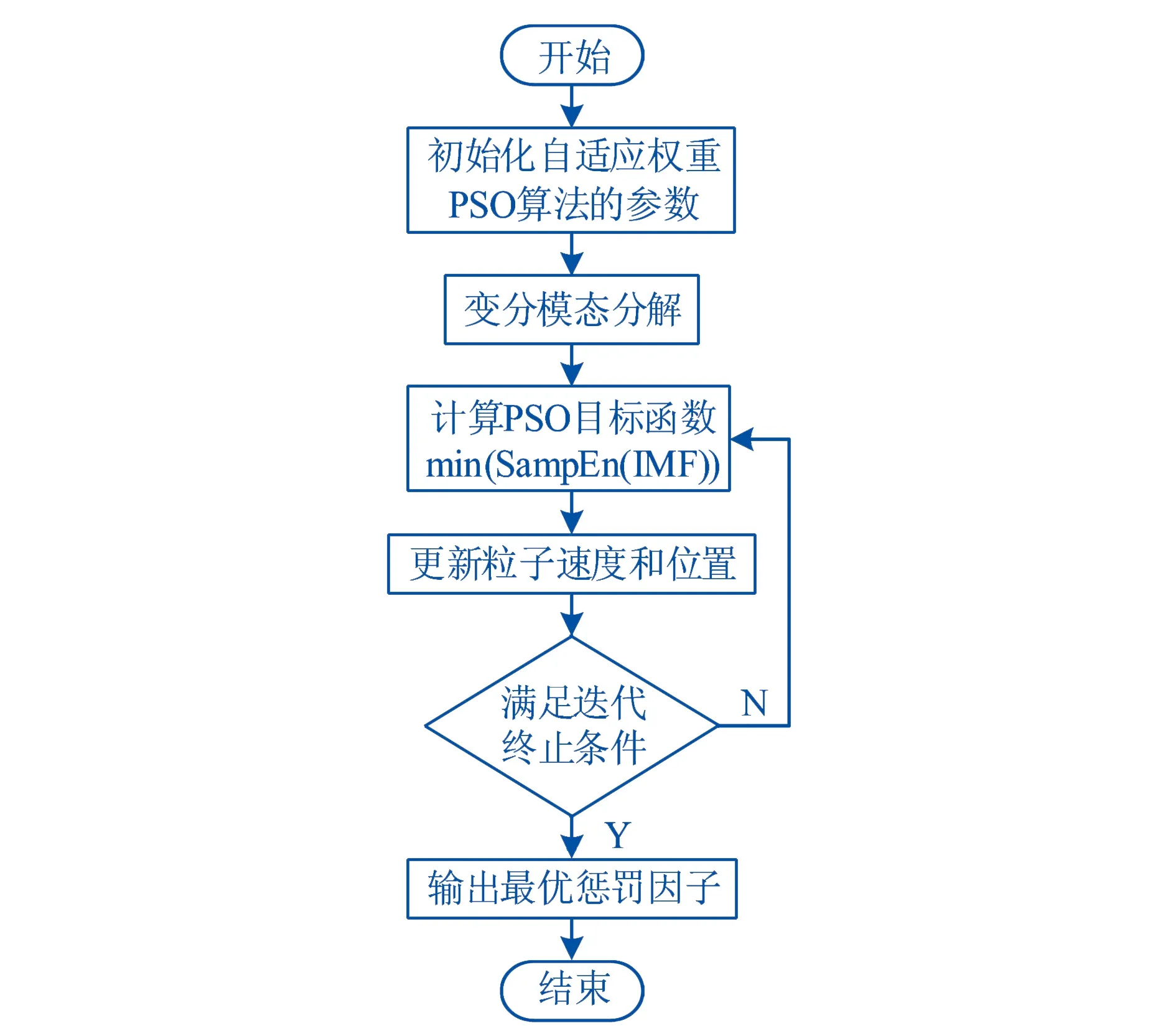
图3 PSO算法寻优VMD参数的流程图
寻优过程采用样本熵的方法[22],其定义为
(10)
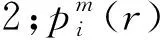
样本熵(Sample Entropy)是时间序列复杂的度量,样本熵越小,序列自我相似性越高;样本熵越大,样本序列越复杂.寻优过程采用样本熵作为度量,获取此条件下VMD分解信号所得的IMF分量,计算所有IMF分量的样本熵并取其最小值,即样本熵局部极小值.以样本熵局部极小值作为PSO寻优过程的适应度函数,将适应度函数取得最小值为寻优目标.寻优过程中,当适应度函数取得最小值时,表明各IMF分量达到最优分离效果,此时对应的惩罚因子α为最优值.
为验证OVMD的分解性能,给定两组混合信号:
(11)
(12)
将这两组混合信号分别用传统的VMD和OVMD进行信号分解,VMD的惩罚因子取固定值300,而OVMD的惩罚因子取寻优后的最优值.
如图4(a)所示,VMD将信号s(t)分解成IMF1分量和IMF2分量,而s(t)经过OVMD分解得到OIMF1分量和OIMF2分量.OVMD寻优得到的惩罚因子最优值为6 906.可以明显看出,OVMD分解得到的OIMF1的波形与s1(t)的波形高度相似,OIMF2的波形与s2(t)的波形也几乎一样,但是VMD分解得到的IMF1和IMF2显然有波形失真,IMF1的波形和幅值与s1(t)有明显差别,IMF2的波形与s2(t)的波形相似但幅值不同.这说明VMD的惩罚因子取值不合适,导致无法很好地将信号分离,而OVMD的惩罚因子经过寻优能取最优的值,使得信号可以完全分解.
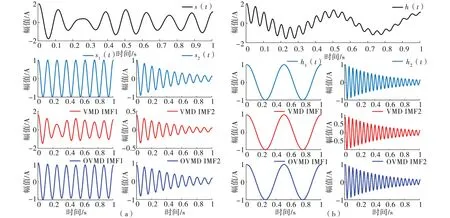
图4 VMD和OVMD分解信号s(t)和h(t)
图4(b)为信号h(t)经过VMD和OVMD分解的对比图.VMD将信号h(t)分解成IMF1分量和IMF2分量,而OVMD将信号h(t)分解为OIMF1分量和OIMF2分量,其惩罚因子寻优得到的最优值为106.可以看出,IMF1和OIMF1的波形与h1(t)的波形高度相似,IMF2和OIMF2的波形与h2(t)的波形非常相似.显然,对于信号h(t),无论是VMD还是OVMD,它们都能较好地将混合信号完全分离.但是从上述两组混合信号的分解对比来看,OVMD有更好的分解效果,对于不同频率的混合信号,惩罚因子选取固定值不能适应所有情况.
2.3 故障特征提取
暂态零序电流成分复杂,本文利用参数寻优的改进变分模态分解对暂态零序电流进行分解,得到衰减直流分量、工频交流分量和高频振荡分量,从而作为后续选线判据的故障特征量.
由于采用两步分解法,所以每一步分解都应该对惩罚因子寻优一次.以故障线路L1为例,在不同的故障条件下,对惩罚因子两次寻优得到的最优值见表1和表2.由表1和表2可以看出,低阻接地时惩罚因子较小,高阻接地时惩罚因子较大.不同的故障情况,对带宽的要求不一样,固定的惩罚因子不能适应所有情况,所以有必要动态调整惩罚因子参数.图5是故障初始角为90°,接地电阻为5 000 Ω时,使用惩罚因子寻优值7 285.938 6和7 708.195 9两步分解零序电流得到的各分量,可以明显看到经过参数寻优后的OVMD能够完整分解出零序电流各分量.

图5 OVMD分解零序电流

表1 第一步的优化值

表2 第二步的优化值
3 基于信息融合的选线判据
计及模态能量和极性等故障特征,本文拟从综合相关系数、相对能量系数和工频分量极性3个方面建立故障选线判据.
3.1 工频分量综合相关系数
由单相接地故障特征可知,在暂态过程中故障线路的工频交流分量与非故障线路的工频交流分量极性相反,当母线故障时各线路极性相同.而且工频交流分量和另外两个分量相比,幅值最大且故障特征最明显,所以可以利用这一特点来选线.
相关性分析能够表征2个或者多个信号波形之间的相似程度,2组离散信号x(j)、y(j)的相似程度可以用ρxy来表示[23],即
(13)
把ρxy称为互相关系数,它是归一化运算的结果,取值区间为[-1,1],-1表示两信号相位相反形状相同,1表示相位形状完全相同,0表示两信号毫无相关性.
利用公式(13)可以求出线路i的特征分量与其他线路的互相关系数,即
ρi=[ρi1,ρi2,…,ρi(i-1),…,ρiN]
.
(14)
取ρi向量所有元素的平均值作为线路i的综合相关系数,可以表示如下:
(15)
在N条线路中,当各线路的综合相关系数差异较大时,综合相关系数最小的为故障线路.当各线路的综合相关系数差异很小,且都接近于1时,则判定为母线故障.
3.2 相对能量系数
由单相接地故障特征分析可知,故障线路暂态零序电流的频率成分复杂且幅值最大,所以故障线路暂态零序电流的能量大于非故障线路,因此该特征可用于选线.当故障初始角为0°时发生接地故障,直流分量最大;当故障初始角为90°时,直流分量最小,而接地故障发生在初始角为90°的概率较大,发生在0°的概率较小.仅仅将直流分量的能量用于选线存在误判风险,所以本文将3个模态分量的能量和用于选线.定义线路i所有模态分量的能量和公式(16)所示.
(16)
所有线路各模态分量的能量值总和为
(17)
利用公式(16)和公式(17)计算出线路Li的能量权重为
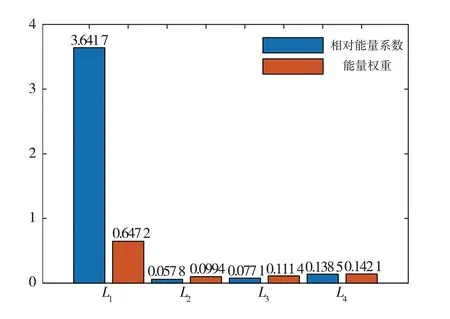
图6 能量权重和相对能量系数

(18)
为了增大能量权重数值差异,以提高选线准确率,本文利用能量权重之间数值上的倍数关系来放大数据之间的差异,即定义相对能量系数
(19)
图6为线路L1故障时各线路的能量权重和相对能量系数对比图,可以看出故障线路与非故障线路的能量权重的数值差距不显著,容易造成误选.经过公式(19)处理后可以看出,故障线路与非故障线路的相对能量系数数据差异明显增大了.
3.3 综合选线判据
对于线路故障,综合相关系数和相对能量系数均能较好地反映故障时的暂态特征,但是暂态零序电流互相关性可能会因受到外界干扰而降低,而单一的能量法也不能适应所有故障情况.所以单一的判据若出现偏差则容易发生误判,选线可靠性不高.因此本文利用信息融合技术的思想,融合工频分量综合相关系数和相对能量系数两种判据,提出综合选线判据.
从消防中介组织和社区委员会的关系来看,政府通过财政支出购买消防中介组织的服务,使消防中介组织能够为社区居委会提供相关的消防培训和教育,针对消防安全事件,能够达到事前预防、事中救援、事后修复的程度,提高社区居民的自救能力。 反之,社区委员会通过对居民意见的收集,针对具体情况,和消防中介组织进行沟通,使消防中介组织的服务落地,根据每个社区不同的情况提供不同的服务,达到效益最大化。
首先将相对能量系数归一化处理,即
(20)
定义线路i的综合选线判据为
(21)
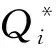
3.4 工频分量极性比较法
故障线路的工频分量极性与其他健全线路相反,因此可作为选线依据.选取一条线路作为参考线路,其他各线路分别和参考线路做暂态零序电流工频分量的内积运算,即
(22)
公式中:i0j(t)为线路j的暂态零序电流工频分量;i0r(t)为参考线路的暂态零序电流工频分量.
当φj>0时,则表示线路j与参考线路同极性,当φj<0则表示反极性.如果参考线路只和一条线路极性相反,则该线路为故障线路;如果参考线路和其他所有线路极性相反,则参考线路为故障线路;如果参考线路和其他所有线路极性相同,则为母线故障.
母线故障时,各线路的综合相关系数差距很小,线路故障时差距较大,传统的方法是通过设定综合相关系数阈值ρst来判断是母线故障还是线路故障.但是暂态零序电流的波形可能会因外界因素干扰而发生变化,致使互相关性降低.仅通过设定阈值无法作为判断母线故障和线路故障的准确分界点,阈值的设定有主观性,存在误判风险.故引入工频分量极性比较法作为判断母线故障和线路故障的辅助判据,即阈值ρst可取较大值,留有较大裕度,本文选取阈值ρst为0.6.当ρmax-ρmin>ρst时,有充分理由认定为线路故障;当ρmax-ρmin≤ρst时,再比较各线路暂态零序电流工频分量的极性,最终确定为母线故障还是线路故障,以达到双重保险的效果.
3.5 选线流程及步骤
故障选线的步骤如下:
(1)当零序电压大于0.1UN,启动算法,同时记录各线路故障时刻前半个周期和故障时刻后两个周期的零序电流;
(2)利用OVMD分解各线路暂态零序电流,得到3个IMF分量,即衰减直流分量、工频交流分量和高频振荡分量;
(3)计算各线路暂态零序电流工频分量的综合相关系数ρi.当ρmax-ρmin>ρst时,判定为线路故障,继续求解各线路的相对能量系数Qi,并融合综合相关系数ρi,最后得到综合选线判据yi,而ymax对应的线路为故障线路.当ρmax-ρmin≤ρst时,再比较各线路工频分量的极性关系,当各线路极性相同,则判定为母线故障;如果各线路极性有唯一不同,则继续求解各线路综合选线判据yi,ymax对应的线路为最终故障线路.
选线流程图如图7所示.
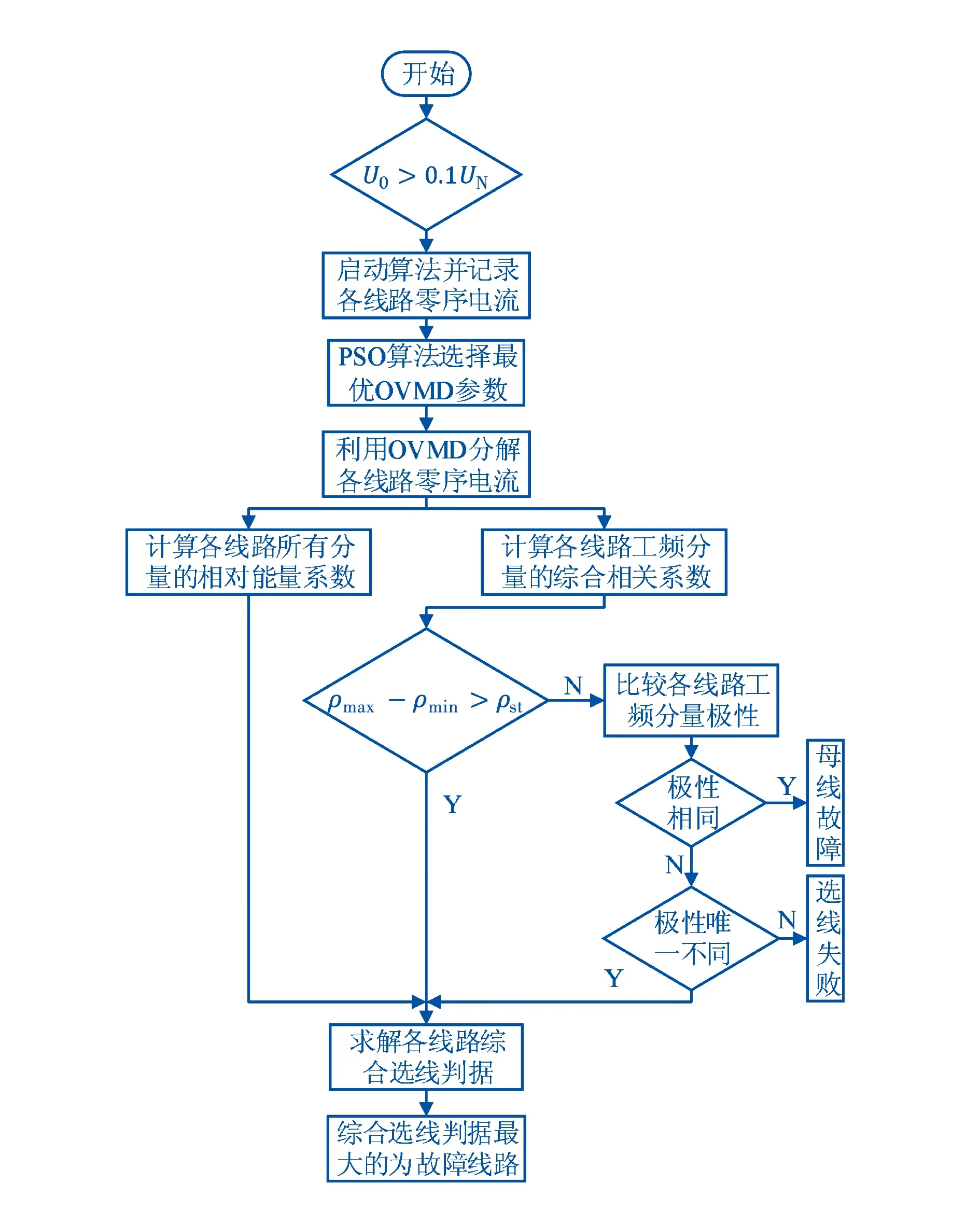
图7 故障选线流程图
4 仿真分析
4.1 仿真模型
为了验证该选线方法的有效性,采用Simulink搭建如图8所示的10 kV的配电网模型进行单相接地故障仿真.由于消弧线圈一般采用过补偿且不高于10%,本文设置消弧线圈的补偿度为8%,消弧线圈计算公式如下:
(23)
公式中:υ=1.08为补偿度;C∑对地电容总和.计算可得消弧线圈的电感值为L=0.678 2 H.根据经验,一般设定消弧线圈串联电阻为感抗的2.0%,经计算可得RL=4.258 8 Ω.
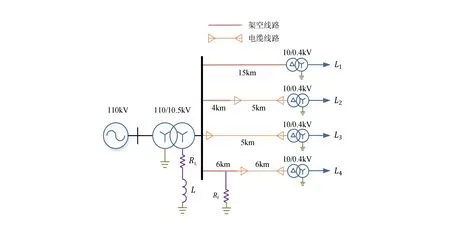
图8 10 kV配电网模型
发生单相接地故障时,暂态零序电流的自由振荡频率的变化范围一般为350 Hz~2 190 Hz[24],因此根据采样定理取采样频率为6 kHz.由于在故障发生后两个工频周期内暂态特征最明显,所以仿真时取故障时刻前半个和后两个工频周期的暂态信号作为研究对象.
考虑到配电网的实际情况,仿真包含了架空、纯电缆和架空-电缆三种类型的线路,该系统共有4条线路,各线路的长度、类型和负荷如表3所示,单位长度线路的正序和零序参数如表4所示[25].

表3 线路的类型、长度和负荷

表4 单位长度(km)线路的参数
4.2 仿真方案
本文设置3个算例进行对比分析,每一个算例对应不同的故障条件,具体仿真方案如表5所示.为了验证本文所提选线方法的有效性,算例1设置为中阻接地、故障初始角最大的故障情况,而算例2和算例3设置为故障初始角较小且高阻接地,同时算例3模拟母线故障时的情形.

表5 仿真方案
4.3 算例1
设定故障线路为L4,当发生单相接地故障时,采集到的各线路零序电流波形如图9所示.各线路的暂态零序电流经过OVMD算法分解后,衰减直流分量、工频交流分量和高频振荡分量被有效分解出来,其分解结果如图10所示.
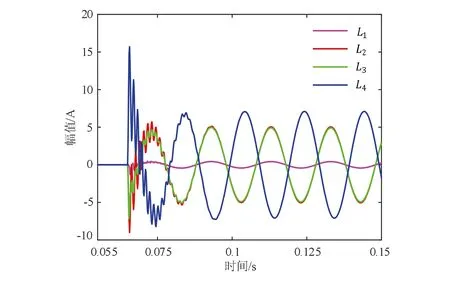
图9 各线路的零序电流

图10 各线路的IMF分量(算例1)
从图10可以看出,线路L4的各分量幅值均最大.与其他线路相比,线路L4的工频分量波形呈反相,初步断定线路L4为故障线路.计算各线路IMF1-2工频分量的综合相关系数ρi,其结果如表6.

表6 算例1的计算结果
由于综合相关系数最大值和最小值之差Δρ=1.279 9,远大于阈值0.6,表明各线路波形差异较大,所以无需再比较工频分量极性,便有充分理由断定为线路故障,而不是母线故障.按照选线流程,继续求解各线路相对能量系数Qi,然后融合综合相关系数ρi,最后求得综合选线判据yi.由表6可以看出,线路L2能量权重q2比线路L4能量权重q4的相对值仅仅小了51.91%,而线路L2相对能量系数Q2却比线路L4相对能量系数Q4小了76.95%,相对能量系数数据之间的差距比能量权重数据之间差距大得多.由于综合选线判据融合了两种判据的故障信息,综合选线判据获得了更高的灵敏度,线路L2的综合选线判据y2比线路L4的综合选线判据y4小了92.31%.线路L4的综合选线判据最大,故判定L4为故障线路,和预先设定的故障线路一致,选线正确.
4.4 算例2
假定线路L3发生单相接地故障,各线路暂态零序电流经过OVMD算法分解后,其衰减直流分量、工频交流分量和高频分量如图11所示.
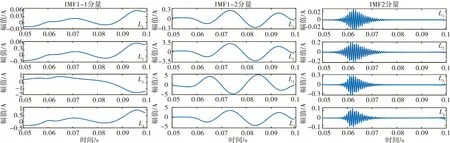
图11 各线路的IMF分量(算例2)
由图11可直观看出,在暂态阶段线路L3含有明显的衰减直流分量,而其他线路的直流分量在0附近波动,几乎不含有直流分量.从图11可知,线路L3和其他线路相比,线路L3的工频分量波形接近反相.计算各线路综合相关系数ρi,计算结果如表7所示.

表7 算例2的计算结果

图12 各线路的IMF1-2分量(算例3)
由于综合相关系数最大值和最小值之差Δρ=1.269 9,远大于阈值0.6,所以可以断定为线路故障而不是母线故障.按照选线流程继续求解各线路相对能量系数Qi,最后求得综合选线判据yi.由表7所示,线路L4的能量权重q4比线路L3的能量权重q3的相对值仅仅小了48.74%,仅凭能量权重作为判据容易造成误判.而线路L4的综合选线判据y4却比线路L3的综合选线判据y3小了91.25%,线路L3的综合选线判据最大且远远大于其他线路,可断定L3为故障线路,选线正确.由此可见,本文提出的综合选线判据在故障初始角很小且高阻接地时,仍能保持较高灵敏度,选线可靠性高.
4.5 算例3
设定母线发生单相接地故障,各线路暂态零序电流的工频分量如图12所示,可以看出各线路工频分量的极性相同.
综合相关系数和工频分量极性的计算结果见表8,由于综合相关系数最大值与最小值之差Δρ小于阈值0.6,按照选线流程,取线路L1为参考线路,再比较各线路工频分量的极性,以最终确定是否为母线故障.由表8所示各线路工频分量极性均大于0,表明其他线路的极性与参考线路L1的极性相同,即所有线路的极性都全部相同,所以无需再计算各线路的综合选线判据,可最终判定为母线故障.

表8 算例3的计算结果
4.6 优越性分析
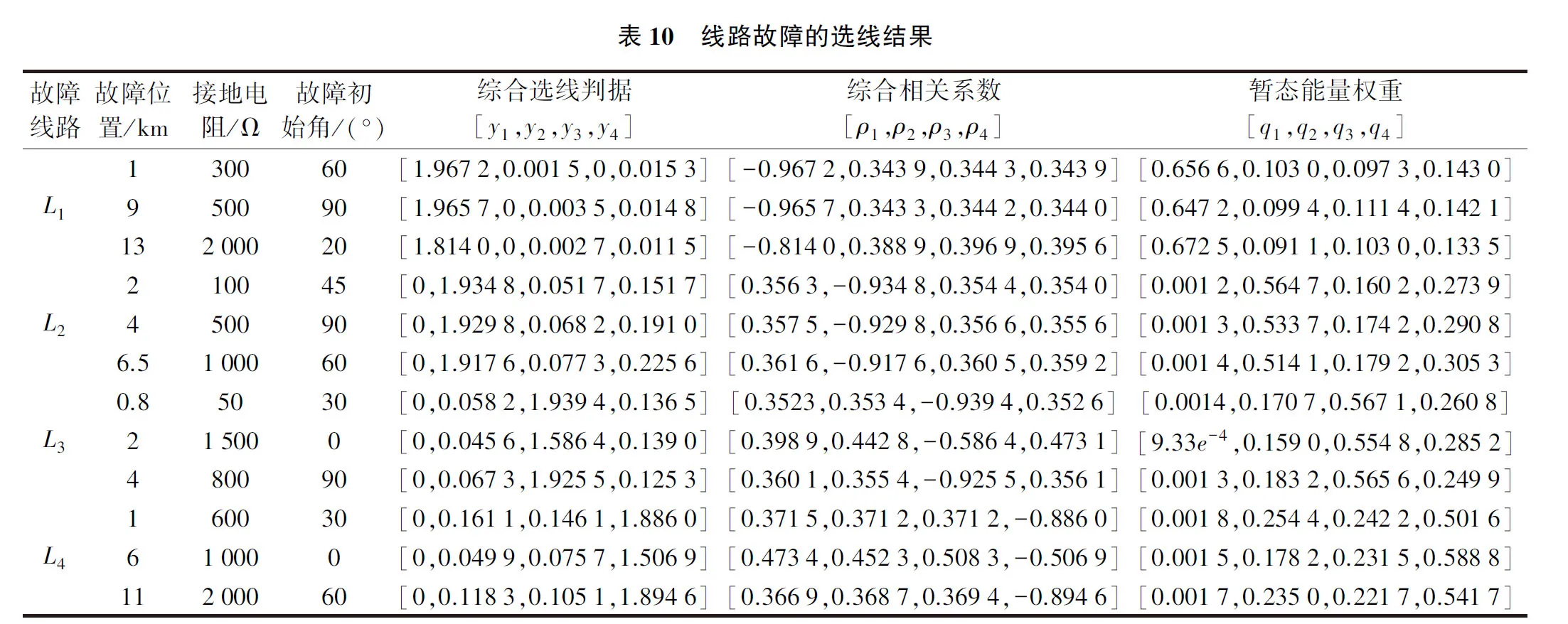
为了验证本文所提选线方法的正确性和优越性,继续对线路不同的故障情况进行仿真分析,并将综合选线判据yi分别与综合相关系数ρi和暂态能量权重qi两种单一判据作比较,仿真数据如表10所示.由表10所示,在所有故障情况下,本文提出的综合选线判据均能正确判断出故障线路,该方法不受故障位置、接地电阻和故障初始角的影响.而且故障线路的综合选线判据数值上都远大于非故障线路,相差两个数量级以上.与综合相关系数和能量权重相比,故障线路和非故障线路的综合选线判据数值之间差异更大,可靠性更高,弥补了单一判据的不足.当故障初始角为0°和20°等较小值且接地电阻较大时,综合选线判据仍然具有很高的灵敏度.
对不同故障条件下的母线故障进行仿真分析,计算结果如表9所示.每种情况下工频分量极性参数均大于0,即各线路极性相同,为母线故障.选线结果与预期一致,可见选线方法正确有效.当有外界干扰时,可能导致互相关性降低,仅凭经验值无法设定准确的阈值作为判别母线故障和线路故障的分界点.而引入工频分量极性比较法作为辅助判据,使得综合相关系数的阈值ρst可选取较大值,留有较大裕度,更可靠地区分母线故障和线路故障.该方法弥补了综合相关系数阈值ρst选取有主观性的缺陷,大大提高了选线准确率.

表9 母线故障的选线结果
5 结 论
本文提出一种基于参数寻优的改进变分模态分解和信息融合的故障选线新方法,通过融合综合相关系数和相对能量系数两种判据,并结合工频分量极性比较法实现选线,能够可靠地辨别出母线故障和线路故障.仿真数据表明:
(1)改进的PSO算法和样本熵法对OVMD的参数选取有一定的优化效果,使得惩罚因子的选取更加合理.OVMD算法相较于传统VMD算法,能够更加有效地分解信号,分解效果更为理想.
(2)综合选线判据有效融合了两种判据,灵敏度更高,弥补了单一判据的不足.引入工频分量极性比较法能够改善综合相关系数阈值选取不合理的问题,减少误判的情况.
(3)选线方法不受故障位置、接地电阻和故障初始角的影响,适应性强,有着较高的可靠性.
