四元数Hermitian张量的特征值反问题及最佳逼近

白 瑞,黄敬频

(广西民族大学 数学与物理学院,广西 南宁 530006)

0 引 言

四元数在人脸识别及数学基础理论研究均有重要作用[1-2].张量(也称超矩阵)在医疗诊断及图像处理等领域有重要作用[3-5].1995年文献[6]阐述了实数域和复数域上有关矩阵特征值反问题的研究进展;2016年文献[7]讨论了自共轭四元数循环矩阵的特征值反问题;2005年祁力群教授在文献[8]提出了超对称张量特征值的概念;2019年文献[9]利用Moore-Penrose广义逆讨论了四元数代数上Sylvester张量方程的可约解;2021年文献[10] 基于Einstein积讨论了复数域上关于张量的特征值反问题.然而,关于四元数体上具有结构张量的特征值反问题目前未见相关的研究报道,针对这一情况,本文提出四元数Hermitian张量的反特征值与最佳逼近问题.

定义1[9]设张量A=(ai1…iMj1…jN)∈I1×…×IM×J1×…×JN,B=(bj1…jNk1…kP)∈J1×…×JN×K1×…×KP，则称为A与B的Einstein积.

定义2设张量A∈I1×…×IM×I1×…×IM,若存在λ∈及非零张量X∈I1×…×IM,使得

A*MX=Xλ(或A*MX=λX),

则称λ为A的右(或左)特征值,而X称为A的属于特征值λ的右(或左)特征张量.

定义3[14]建立张量A到矩阵A的1-1映射f:SI1,I2,…,IN,J1,J2,…,JN()→TI1I2…IN,J1J2…JN(),其分量对应关系为

则称f是张量A的转换算子,记作f(A)=A.

本文具体提出并讨论如下两个问题:

问题1给定s个四元数张量特征对(Xi,λi),其中Xi∈I1×…×IM,λi∈,i=1,2,…,s且求张量使得:

B*MXi=Xiλi,i=1,2,…,s

(1)

问题2设问题1的解集σ非空,M∈I1×…×IM×I1×…×IM是给定的张量,在σ中求四元数张量使得:

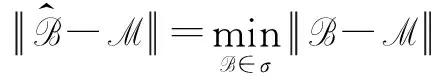
(2)

1 问题1的解

为说明问题1的合理性,首先证明任意一个四元数Hermitian张量的特征值均为实数.对此,先给出下面两个引理.

引理1[2]设A=A*∈n×n是四元数自共轭矩阵,则存在四元数酉矩阵U使得UAU*=diag(c1,c2,…,cn),其中ci∈,i=1,2,…,n是A的n个实特征值.

引理2设张量A=A*∈I1×I2×…×IN×I1×I2×…×IN是四元数Hermitian张量,则存在四元数酉张量U使得:

U*NA*NU*=Z

(3)

其中张量Z=(zi1i2…iNj1j2…jN)∈I1×I2×…×IN×I1×I2×…×IN的元素为:

(4)

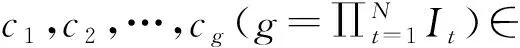
证明设张量A的转换矩阵A=f(A),由A=A*及算子f的性质可知A=A*是自共轭矩阵[2].由引理1,存在四元数酉矩阵U使得:

A=U*ZU=U*diag(c1,c2,…,cg)U

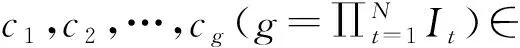
f-1(A)=f-1(U*ZU)=f-1(U*)*Nf-1(Z)*Nf-1(U)

⟹A=U**NZ*NU⟹U*NA*NU*=Z,

其中:U=f-1(U)是四元数酉张量,Z=f-1(Z)是形如(4)的实张量.证毕.

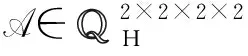
a1111=1,a1121=-k,a1112=-i,a1122=j,a2111=k,a2121=1,a2112=-2j,a2122=i,
a1211=i,a1221=2j,a1212=7,a1222=-k,a2211=-j,a2221=-i,a2212=k,a2222=1.

则由定义3及自共轭四元数矩阵的酉对角分解可得：

这里U∈4×4是一个四元数酉矩阵,Z=diag(1,-1,2,8).于是由转换算子f的逆算子可得A=f-1(U*)*2f-1(Z)*2f-1(U),其中U=f-1(U)∈2×2×2×2是一个酉张量,其元素为:

又因为：

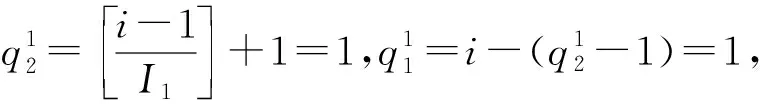
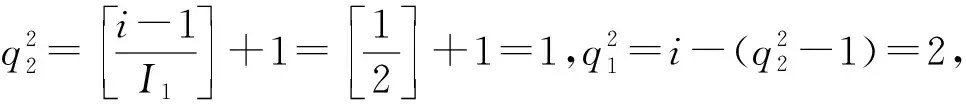
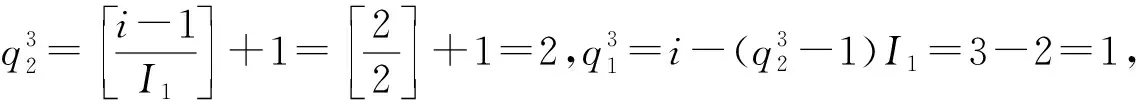
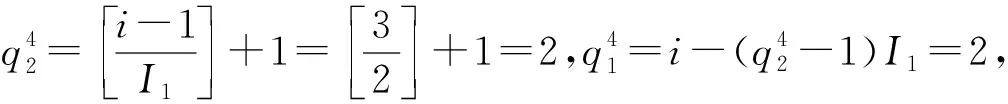
所以，实张量Z=f-1(Z)=(zi1i2j1j2)∈2×2×2×2的元素为:

根据引理2可知,四元数Hermitian张量的特征值全为实数.对问题1所给的s个四元数张量特征对(Xi,λi),记:

X=[X1,X2,…,Xs]∈I1×I2×…×IM×s,D=[X1λ1,X2λ2,…,Xsλs]∈I1×I2×…×IM×s

(5)

于是关于问题1的解可转化为求解下列四元数张量方程:

B*MX=D,B*=B

(6)

定理1张量方程(6)的可解性等价于张量方程组：

(7)

的可解性.

证明若张量方程(6)有解,可得张量方程(7)也有解.反之,给定A为张量方程组(7)的一个解,则由[(A+A*)/ 2]*=(A+A*)/2可知,B=(A+A*)/2为Hermitian张量且满足方程(6).证毕.

定理1表明,只要得到张量方程组(7)的一般解,就可得到问题1的解.因此，只需考虑张量方程组(7)的求解问题.

定理2设张量A1∈K1×…×KN×J1×…×JN,D1∈K1×…×KN×J1×…×JN,A2∈J1×…×JN×P1×…×PN,D2∈J1×…×JN×P1×…×PN,则张量方程组：

(8)

有解的充要条件为:

(9)

此时它的通解为:

(10)

其中V为任意张量.

证明若(8)有解X1,则由A1*NX1=D1,X1*NA2=D2可得

A1*ND2=A1*N(X1*NA2)=(A1*NX1)*NA2=D1*NA2,

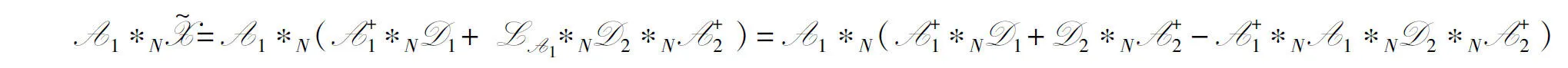
可知X1包含在(10)之中.证毕.

根据定理1和定理2,可得问题1的解.

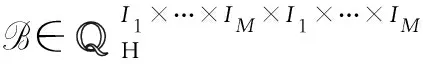
X**MD=D**MX,D*1X+*MX=D

(11)

其中X,D如(5)所示.当(11)成立时,B的通解表达式为:

(12)

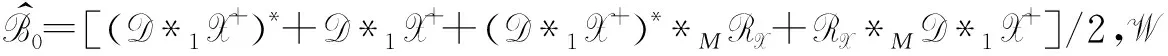
证明根据定理2,立即可得张量方程组(7)有解的充要条件为(11)成立.在此条件下,张量方程组(7)关于B的通解为:

B=(X*)+*1D*+ LX**MD*1X++ LX**MY*MRX

(13)

B=(D*1X+)*+RX*MD*1X++RX*MY*MRX

(14)

其中Y为任意四元数张量.结合(14)和定理1可知,(12)即为四元数张量方程(6)的通解表达式.证毕.

证明由(5)式可令D=X*1Λ,其中Λ=diag(λ1,λ2,…,λs),则由张量内积的定义以及X+*MRX=0,RX*MX=0,得:

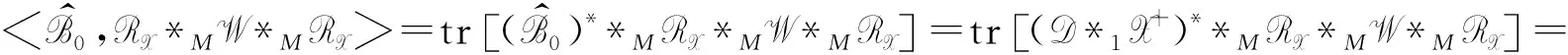
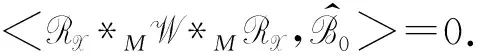
(15)

2 问题2的解

为讨论问题2的解,先给出下面的引理.

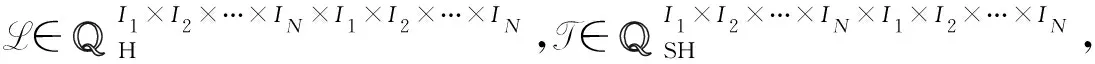
证明令N=L*NT-T*NL,则由L*=L,T*=-T可知N*=N,从而tr(N)=Re[tr(N)].又由文献[2]定理4.2.10和张量内积的定义可得Re[tr(L*NT)]=Re[tr(T*NL)],所以:

⟨L,T⟩+⟨T,L⟩=tr(L**NT)+tr(T**NL)=tr(L**NT+T**NL)=tr(L*NT-T*NL)=tr(N)=
Re[tr(N)]=Re[tr(L*NT-T*NL)]=Re[tr(L*NT)]-Re[tr(T*NL)]=0,

证毕.

于是关于问题2的解,有如下结果:

定理5设问题1的解集σ非空,M∈I1×…×IM×I1×…×IM为一给定的四元数张量,则存在Hermitian张量:

(16)

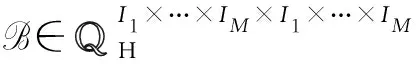
(17)

于是由(17)及张量的Frobenius范数定义得:

(18)

把问题1的通解表达式(12)代入(18)可得:

(19)

因此，由(19)可知:

(20)

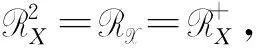
(21)

3 数值算例

例2给定四元数张量如下4个特征对

则可得:

X=[X1,X2,…,Xs]∈I1×I2×…×IM×s,D=[X1λ1,X2λ2,…,Xsλs]∈I1×I2×…×IM×s.

X(:,:,1)=X1,X(:,:,2)=X2,X(:,:,3)=X3,X(:,:,4)=X4,
D(:,:,1)=X1λ1,D(:,:,2)=X2λ2,D(:,:,3)=X3λ3,D(:,:,4)=X4λ4.

利用Matlab软件计算可得张量D:

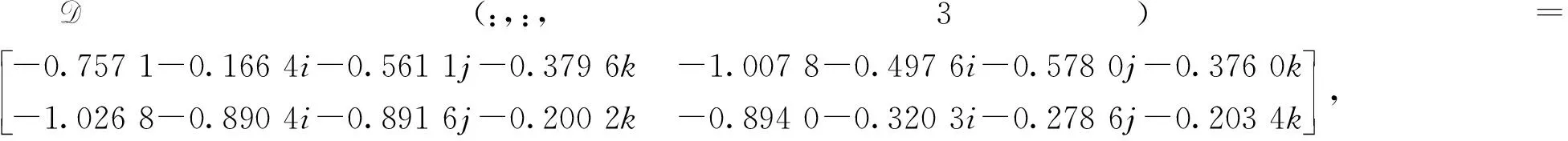
张量X的Moore-Penrose 广义逆为:

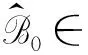
由于X*1X+=I,因此RX=0,这时对于任意给定的M∈2×2×2×2,问题2的最佳逼近解为

4 结 论

讨论了基于Einstein积的四元数Hermitian张量的特征值反问题.对给定的s个四元数张量特征对,主要通过张量的转换算子和张量的Moore-Penrose广义逆,获得问题1有解的充要条件以及通解表达式.对于最佳逼近问题2,根据张量范数的性质,得到其最佳逼近解.本文结果把四元数矩阵的特征值反问题推广到了四元数结构张量的特征值反问题,拓广了四元数张量的相关结果.