基于Res-LSTM的燃料电池系统故障检测
2023-01-03乐有生常雨芳谭保华
全 睿,乐有生,李 涛,常雨芳,谭保华
(1.湖北工业大学 太阳能高效利用及储能运行控制湖北省重点实验室,湖北 武汉 430068;2.湖北工业大学 电气与电子工程学院,湖北 武汉,430068; 3.湖北工业大学 理学院,湖北 武汉 430068)
0 引言
质子交换膜燃料电池(Proton Exchange Membrane Fuel Cell,PEMFC)是一种环境友好、零碳或低碳的能量转换装置,具有良好的发展前景.PEMFC系统由多个子系统组成,PEMFC电堆的物理化学机理复杂,因而PEMFC系统易发生多种故障.对PEMFC系统进行故障检测,可以获取系统的运行信息,有利于提高系统的可靠性.
Wang等[1-4]对PEMFC系统故障诊断方法进行了综述,为相关研究提供了重要参考;Oh等[5]使用解析冗余值和测量值的残差作为指标,开发了一种检测和诊断热管理系统部件故障的方法;Polverino等[6]通过结构分析辨识系统涉及的物理量和系统可能的故障间的关系,开发集总参数模型,以因果关系算法分析设计残差发生器检测和隔离故障;Yang等[7]采用线性参数可变模型描述PEMFC系统行为,提出增强状态观测器估计系统内部状态和组件故障;王筱彤等[8]提出一种基于离散区间二进制序列脉冲信号的燃料电池电化学阻抗谱在线测量及故障诊断方法.这些基于模型的方法建立燃料电池的机理模型进行故障的检测和诊断,需要深入研究PEMFC的模型.机理模型需要利用流体力学、电化学、热力学等多方面知识建立PEMFC的多维物理模型.目前还难以建立覆盖多种类型的燃料电池故障模型,同时也面临着部分参数获取的难题.余嘉熹等[9]基于Bootstrap法和随机森林算法对燃料电池系统的故障进行分类.刘嘉蔚等[10]基于在线序列超限学习机和主成分分析进行燃料电池的故障诊断;文献[11]提出基于概率神经网络和线性判别分析的燃料电池水管理系统故障诊断;文献[12]采用K均值和支持向量机算法进行车用燃料电池系统的故障诊断.这些基于非模型的方法需要正常和有针对性故障条件下的大量历史数据,完全依赖传感器数据和相关信号.PEMFC系统数据的丰富程度对算法性能有着重要的直接影响.特别是故障数据获取成本高,难以大量获取,容易造成算法的诊断效率不高.
PEMFC系统的故障运行试验在实验室条件下具有一定可行性,然而大范围推广应用的成本高,部分故障运行试验可能造成燃料电池堆的性能退化甚至不可逆损毁.PEMFC系统的正常运行数据却更容易获取,获取成本也更低廉.神经网络算法是一种模仿生物神经网络行为的信息处理算法,可以用来建立燃料电池的输入输出预测模型.通过采集质子交换膜燃料电池系统的运行数据,运用神经网络拟合燃料电池系统多变量间的映射关系,无需分析系统的机理模型,可以便捷地从数据中发掘燃料电池系统的输入输出关系.长短期记忆(Long Short-Term Memory,LSTM)网络是一类适用于时序数据处理的神经网络.残差网络(Residual Network,ResNet)引入残差学习结构可以大幅提高网络深度,同时也更容易训练出高性能的网络.本文将残差网络和长短期记忆网络结合形成残差-长短期记忆网络(Residual Network with Long Short-Term Memory,Res-LSTM),基于大量PEMFC系统的正常运行状态数据对系统进行模拟,通过预测PEMFC系统的输出电压进行状态检测,检测系统是否存在故障.
1 基于Res-LSTM模型的检测方法
1.1 质子交换膜燃料电池系统故障检测方案
本文采用的基于Res-LSTM模型的质子交换膜燃料电池系统故障检测方案如图1所示.该方案根据PEMFC系统的正常运行数据,运用Res-LSTM模型拟合燃料电池系统的运行行为,得到PEMFC系统输入输出关系模型.在故障检测时,首先Res-LSTM模型根据系统当前输入数据预测燃料电池的输出电压,然后根据PEMFC系统的实际输出电压与Res-LSTM模型的预测输出电压的电压残差判断系统有无故障.

图1 基于Res-LSTM的PEMFC系统故障检测方案Fig.1 The fault detection scheme of PEMFC system based on Res-LSTM
残差处理主要对电压残差进行统计分析,为设置电压残差阈值提供参考.本文设置电压残差阈值为三倍测试数据电压残差标准差.假设电压残差为R,测试数据的电压残差标准差为σ,电压残差阈值为Rth,设置电压残差阈值Rth=3σ.故障判断规则为:当|R|>Rth时判定质子交换膜燃料电池系统处于故障运行状态,否则判断为正常运行状态.
1.2 Res-LSTM模型
本文结合残差网络和长短期记忆网络的结构和性能特点,提出采用残差-长短期记忆网络拟合燃料电池系统模型,建立燃料电池系统的预测模型进行故障检测.
残差网络(Residual Network,ResNet)通过在网络层间引入短路连接形成残差进行残差学习[13-14].残差网络的基本单元是残差块,其示意图如图2所示.输入x经过L个神经网络层变换得到F(x),F(x)再加上输入x得到输出.假设输出为y,则残差块的计算如(1)式所示;若多层神经网络变换后得到的F(x)与x维度不同,可以采用线性投影矩阵W对输入x进行维度变换获得与F(x)匹配的维度,此时残差块的计算如(2)式所示[13-14]:
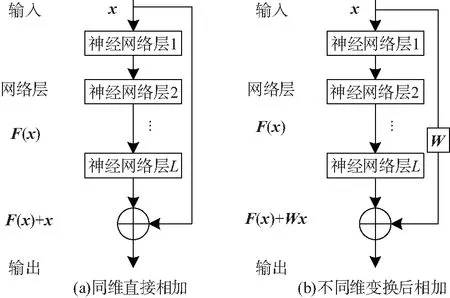
图2 残差块示意图Fig.2 The residual block diagram
y=F(x)+x
(1)
y=F(x)+Wx
(2)
将多个不同的残差块堆叠可以形成深度残差网络.残差网络能够大幅提高神经网络的深度,有效避免深层神经网络的退化问题,同时获得更好的性能[13-14].
LSTM网络是一类适用于序列数据处理的循环神经网络.深层LSTM网络由LSTM网络层逐层堆叠形成.LSTM网络层的结构如图3所示.LSTM网络层由多个LSTM神经元有序连接组成,同一网络层内的LSTM神经元共享网络参数.LSTM神经元包含遗忘门、输入门、输出门3个门控开关.假设x=[x1,x2,…,xN]表示网络层的输入,xt∈Rd(t=1,2,…,N)表示网络层在第t时刻的输入,d表示输入数据的维度;h=[h1,h2,…,hN]表示网络层的输出,ht∈RD表示网络在第t时刻的输出,D表示输出数据的维度;gft表示网络层的第t个遗忘门(下标f表示英文遗忘forget,便于与其他门区别),git表示网络层的第t个输入门(下标i表示英文输入input,便于与其他门区别),got表示网络层的第t个输出门(下标o表示英文输出output,便于与其他门区别).遗忘门gft控制接收上一个神经元的内部状态信息程度;输入门git控制接收当前神经元的输入信息程度;输出门got控制当前神经元的输出信息程度.LSTM网络层通过同一层的LSTM神经元参数共享降低了网络参数量.LSTM神经元的计算方式为[15-16]:
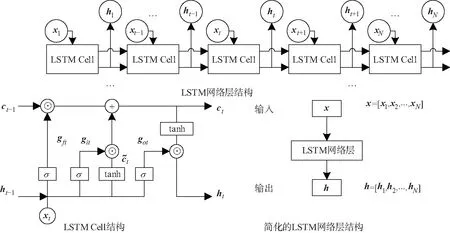
图3 LSTM网络层结构示意图(LSTM Cell:LSTM神经元)Fig.3 The structure diagram of LSTM network layer
gft=σ(Wfhht-1+Wfxxt+bf)
(3)
git=σ(Wihht-1+Wixxt+bi)
(4)
(5)
(6)
got=σ(Wohht-1+Woxxt+bo)
(7)
ht=got⊗tanh(ct)
(8)
式中:⊗表示两个同维向量或矩阵对应元素相乘运算;t=1,2,…,N,N为网络层的LSTM神经元个数;c0=0,h0=0;Wfh、Wfx、Wih、Wix、Wch、Wcx、Woh、Wox是LSTM神经元的权值参数矩阵,其中Wfh表示因变量gft与自变量ht-1间的权值矩阵,其他依次类推;bf、bi、bc、bo是LSTM神经元的偏置参数向量,其中bf表示gft的偏置向量,其他依次类推.σ表示sigmoid激活函数,表达式如(9)所示[16],tanh激活函数的表达式如(10)所示[16]:
(9)
(10)
式中:激活函数均为按元素计算.
基于ResNet和LSTM网络的结构和性能特点,本文提出采用Res-LSTM建立燃料电池系统模型.Res-LSTM在LSTM的基础上引入残差学习机制,结合了ResNet和LSTM网络的优点.Res-LSTM网络层的结构如图4所示.Res-LSTM网络层通过残差网络的短路连接将残差学习引入到LSTM网络层中,LSTM神经元和LSTM网络层的模型不变,仅在原来的LSTM网络层的输出上叠加了网络的输入.Res-LSTM网络层的无投影矩阵和有投影矩阵的输出计算公式如式(11)和式(12)所示:

图4 Res-LSTM网络层结构示意图Fig.4 The structure diagram of network layer in the Res-LSTM
ot=ht+xt
(11)
ot=ht+Wxt
(12)
1.3 数据预处理及燃料电池系统数据集
PEMFC系统主要由氢气供给系统、空气供给系统、燃料电池堆、水热管理系统、数据采集和控制系统等组成.通过台架运行实验和车载路测实验,本文获取了大量质子交换膜燃料电池系统的正常状态运行数据.在剔除部分缺失或不全的数据后,对数据进行归一化处理,消除各维变量物理单位差异、数量级差异等对神经网络训练的影响.采用最大最小化数据预处理方法,即假设zi是各维变量原始数据,zi′是标准化处理后的数据,zi,min是变量原始数据的最小值,zi,max是变量原始数据的最大值,归一化处理的计算公式如(13)式所示:
(13)
对预处理后的数据进行整理,得到燃料电池系统数据集,如表1所示.数据集共有 42 997 个样本,每个样本由(x,y)组成.x代表神经网络的输入,y代表相应的电堆1#电压和电堆2#电压的真实值.选取的检测输入变量共有20维,时间序列长度为10,时间间隔周期为 1 s.

表1 燃料电池系统数据集Tab.1 The fuel cell system dataset
按8∶2的比例将数据集随机划分为训练集和测试集,即训练集共有 34 397 个样本,测试集共有 8 600 个样本.训练集和测试集分别用于训练网络和对完成训练的网络进行测试评估.
1.4 Res-LSTM模型的结构配置及训练
图5为LSTM网络和Res-LSTM模型的网络结构,LSTM网络和Res-LSTM模型的LSTM网络层设置相同.本文设计的Res-LSTM模型的结构配置如图5(c)Res-LSTM11-10所示.整个Res-LSTM模型共由11层LSTM网络层组成,含有10个残差块,每层的LSTM网络层共有10个神经元,各层每个神经元的输出数据维度分别为16,10,10,10,8,8,8,4,4,4,2.图中右侧实线表示短路连接没有线性变换,右侧虚线表示短路连接有线性变换.网络输入10个时刻的20维向量数据xi(i=1,2,…,10),故N=10.向量xi各维的数据意义如表1所示,每个时刻间隔周期为 1 s.前一个网络层的输出作为后一个网络层的输入.最后一个网络层输出最后一个时刻的数据u,即为电堆1#电压、电堆2#电压的预测值.

图5 LSTM网络与Res-LSTM结构配置(N=10)Fig.5 The structure configurations of LSTM network and Res-LSTMs (N=10)
在网络训练时需要选定损失函数,本文使用均方差损失函数.假设Res-LSTM模型的预测值为u=f(x;θ),θ表示神经网络的参数集,预测的真实值为y,均方差损失函数L的计算方法为:
(14)

针对大规模数据通常采用小批量梯度下降法训练神经网络.Adam算法[17]是一种小批量梯度下降法的改进算法,本文采用Adam算法进行网络参数更新.Adam算法不仅对学习率进行自适应调整,而且对梯度进行修正.假设每次从训练集选取B个样本组成一个批量,Adam算法计算方法为[17]:
(15)
(16)
Mt=β1Mt-1+(1-β1)gt
(17)
(18)
(19)
(20)
(21)
θt=θt-1-Δθt
(22)
式中:r表示某一个批量的样本序号,B为批量大小,M0=0,G0=0,α为初始学习率,β1、β2为衰减率,ε是防止除零错误的小常数.本文设置B=64,α=0.001,β1=0.9,β2=0.999,ε=10-7.
在网络训练时,每轮训练后计算在训练集和测试集的均方差损失函数和所有预测变量的平均绝对误差.均方差损失函数用于衡量网络训练的性能.平均绝对误差MAE用于衡量预测误差的大小:
(23)
式中,各量的意义同(14)式.
1.5 实验结果及残差阈值设置
本实验使用的软件为Python3.7.10和TensoFlow-GPU2.3.0.
在训练过程中,训练集和测试集的均方差损失和平均绝对误差的变化如图6所示.在前14轮训练过程中,训练集和测试集的均方差损失和平均绝对误差呈快速减小趋势,第14轮以后均方差损失和平均绝对误差减小趋势变缓.从图6中可以看到,在训练集和测试集上,第39轮训练后的均方差损失和平均绝对误差都为最小值.为选出性能最好的模型,选择第39轮训练后的网络模型参数作为最终的Res-LSTM模型参数.此时训练集的均方差损失和平均绝对误差约为 0.000 70 和 0.009 18,测试集的均方差损失和平均绝对误差约为 0.001 01 和 0.009 77.

(a)均方差损失 (b)平均绝对误差图6 训练集和测试集每轮均方差损失和平均绝对误差变化Fig.6 Mean square error loss and mean absolute error versus epoch on training set and test set
使用最终得到的Res-LSTM模型对 8 600 个测试集样本进行测试,计算得到电堆1#电压预测误差均值和标准差分别大约为μ1=0.000 68 和σ1=0.031 79,电堆2#电压预测误差均值和标准差分别大约为μ2=-0.000 31 和σ2=0.031 76.计算结果表明测试集样本的预测误差的均值非常接近于0.图7和图8显示了Res-LSTM模型在测试集上的电堆1#电压和电堆2#电压的预测误差.除了极少部分样本外,大部分样本的电压预测误差均分布在[-3σ1,3σ1]和[-3σ2,3σ2]误差带内.
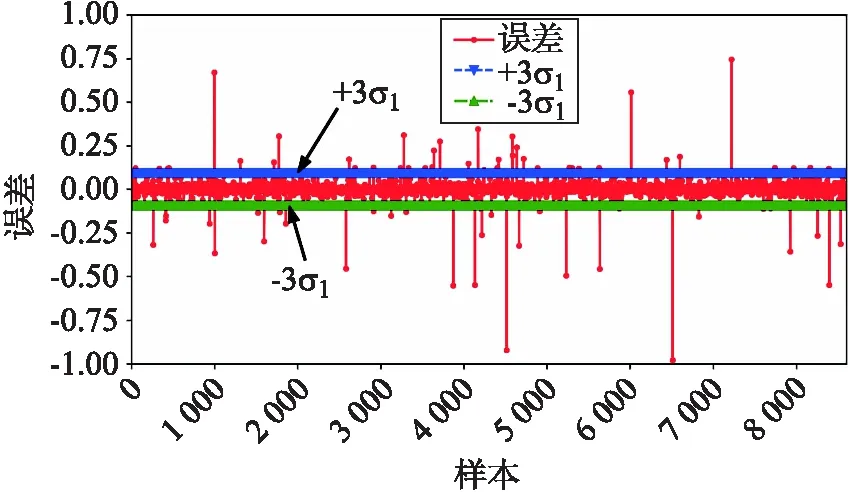
(数据已归一化,纵轴为无量纲量)图7 测试集电堆1#电压预测误差Fig.7 1# stack predicted voltage error on test set

(数据已归一化,纵轴为无量纲量)图8 测试集电堆2#电压预测误差Fig.8 2# stack predicted voltage error on test set
根据对预测误差的分析,设定电堆1#电压残差阈值R1th=3σ1=0.095 37,电堆2#电压残差阈值R2th=3σ2=0.095 28.在进行故障检测时,设定当电堆1#电压残差或电堆2#电压残差的绝对值超出阈值时即判定燃料电池系统运行出现故障.图9分别为采用Res-LSTM模型预测的38组故障样本的电堆1#和电堆2#电压残差,图中显示故障样本的电压残差超出电压残差阈值.
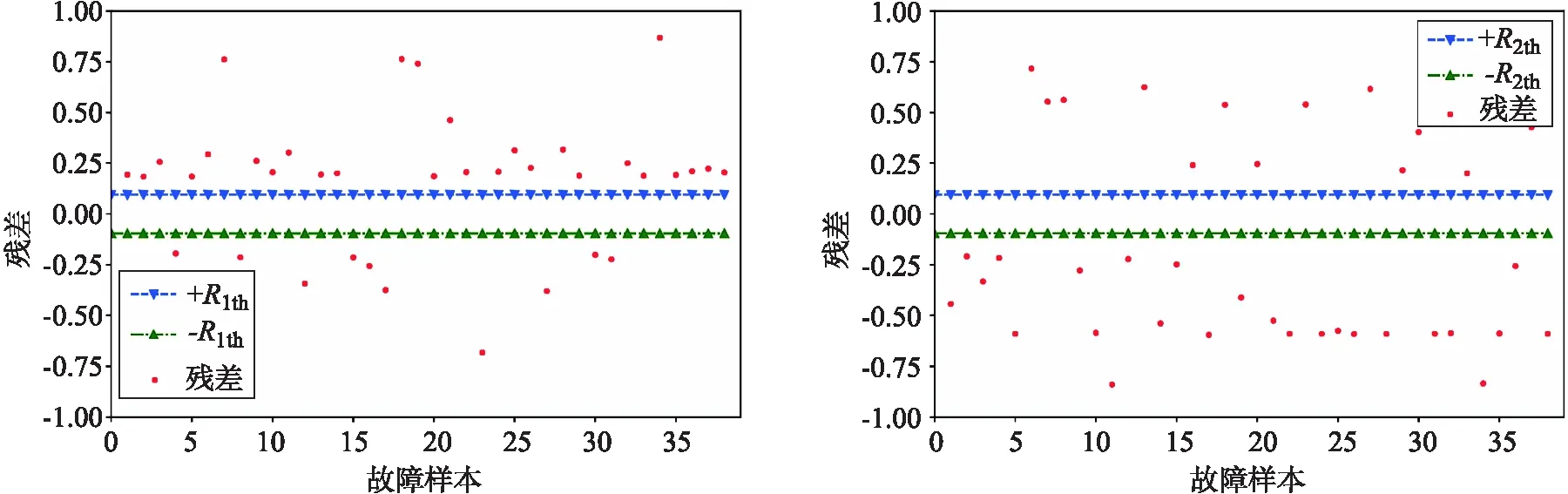
(a)1# (b)2#(数据已归一化,纵轴为无量纲量)图9 电堆1#/2#电压残差Fig.9 1#/2# stack voltage residual
2 LSTM网络和Res-LSTM模型的比较
图5为3种不同的神经网络结构.图5(a)是LSTM网络,图5(b)、5(c)是对应的采用不同数量残差块的Res-LSTM模型.图5(a)、5(b)、5(c)的各个LSTM网络层的设置相同,已在1.4小节说明.图5所示的3个不同结构的网络的实验实现及结果如表2所示,表中所选模型均为40轮训练过程中在训练集上均方差损失最小的网络模型.除表2所列设置外,其他实验设置均相同.
表2实验结果表明,在均方差损失、预测误差均值、预测误差标准差等指标上,Res-LSTM模型比具有相同LSTM网络层的LSTM网络性能表现更好.Res-LSTM模型的训练集均方差损失和预测电压误差标准差更小,预测电压误差均值更接近于0.相比LSTM网络,Res-LSTM在性能上具有全面的提升,特别是在网络参数量相同时,Res-LSTM模型相比LSTM网络依然具有全面的性能优势.图10显示了LSTM网络和Res-LSTM模型在训练过程中训练集上的均方差损失的变化.相比LSTM网络,Res-LSTM模型的均方差损失更快收敛,训练速度更快.对于相同的Res-LSTM模型,Adam算法比RMSprop算法的训练速度更快.

表2 LSTM网络和Res-LSTM的实验比较Tab.2 Experimental comparisons of LSTM network and Res-LSTMs

图10 LSTM网络和Res-LSTM在训练集上的均方差损失变化Fig.10 Mean square error loss versus epoch on training set
3 结论
本文针对质子交换膜燃料电池系统故障检测问题,提出采用Res-LSTM模型拟合的方法建立质子交换膜燃料电池模型,根据实际系统输出电压与网络预测电压的电压残差判断系统是否存在故障.Res-LSTM模型的实验显示可以很好地拟合燃料电池数据,可以在不考虑燃料电池系统复杂的机理模型的情况下进行故障检测.实验表明,相比LSTM网络,Res-LSTM模型的预测性能更好,网络训练速度更快,电压残差阈值更小,从而可以获得更准确的故障检测结果.
