MEA-BP神经网络在预测地震模拟试验数据中的应用
2023-01-03俞树荣尹思敏薛睿渊李勇霖
俞树荣,尹思敏,薛睿渊,李勇霖
(兰州理工大学石油化工学院,甘肃 兰州 730050)
地震台模拟试验是对核电阀门管道系统进行抗震鉴定的主要手段。试验过程中加速度测量计的损坏会导致试验数据测量不完整,严重者将导致整个试验失败。因此,地震模拟试验中如何补全缺失的试验数据是一项重要工作。补全数据最基本的方法是重新进行试验,如果在试验现场发现某些测量仪损坏可重新进行试验。如果在试验现场未能发现该问题,则由于试验台拆卸、试验场地预约等问题导致补做试验成本过高,使得重新进行试验基本不可行。目前已有研究中针对如何解决地震模拟试验中振动数据测量不完整的问题鲜有报道。
神经网络因其具有大规模的并行处理和分布式的信息储存能力,极强的自学、联想和容错能力,良好的自适应性和自组织性,多输入、多输出的非线性拟合系统等特征,已在地震预测、结构振动主动控制等领域得到广泛应用[1-4]。神经网络还具有不需要建立数学模型以及对未知系统具有辨识和预测能力的优点,而常被作为数据预测的工具,如张永举等[5]利用BP神经网络在进行少量试验的情况下预测了不同试验条件的结果。由此可见神经网络有潜力预测地震模拟试验中测量不完全的响应数据。
研究首先介绍了已经完成的“阀门管道系统地震模拟试验”中管道结构响应中加速度测量计损坏导致的某些测点加速度数据测量不完整的情况,然后利用神经网络对未测得的数据进行预测,以便补全该测点加速度响应时程曲线。
预测过程中随机选取同一工况下管道结构中测得完整数据的加速度测点训练神经网络,利用相关系数法确定神经网络的输入集,利用试错法逐步确定神经网络最佳拓扑结构并验证网络结构的适用性,最后利用训练得到的最优网络拓扑结构对测点中缺失的加速度数据进行预测。
1 振动台试验概述
为研究核电阀门管道系统中阀门和管道的动态耦合作用,讨论阀门管道系统在地震期间的动态行为,研究设计了未安装阀门的管道系统和安装有阀门的管道系统的“阀门管道系统地震模拟试验”。未安装阀门的管道结构及其测点布置细节如图1所示,模型中管单元的节点与试验测点位置一一对应,使用测点的位置编号指代节点。

图1 管道试验细节及加速度测量计布置Fig.1 Details of pipeline test and arrangement of accelerometer
图1中管道结构总长为3 470 mm,管道壁厚为4 mm,外径为48 mm,两端通过螺母固定在支架上。试验过程中共设置13个加速度测点,其中12个分布在管道上,1个放置在振动台面上用来测量振动台加速度数据。本次试验中使用的加速度测量计的采样时间为0.001 s,并利用电液伺服地震模拟振动台提供激励,试验过程中管道结构相关工况如表1所列。

表1 管道结构试验工况细节Table 1 Details of piping structural test conditions
由于管道结构在Y和Z方向完全对称,因此试验过程只为其设计了Y方向试验。表1中工况1是为了探查管道结构的动态特性。为了研究管道结构在不同地震激励下的响应,向管道结构的抗震裕度分析提供试验数据,为其设计了2种幅值不同的人工地震波试验,即工况2和工况3。工况2使用的人工地震波最大幅值为13.2 m/s2,见图2(a);工况3中使用的人工地震波最大幅值为8.6 m/s2,见图2(b)。

图2 人工地震波时程曲线Fig.2 Time curve of seismic wave
在工况2中响应最大位置测点7测得的加速度时程曲线如图3所示。

图3 工况2测点7加速度曲线Fig.3 Acceleration curve of measuring point 7 in working condition 2
由图3可知,该测点的响应时程曲线中17.226~17.228 s、17.338~17.344 s和17.399~17.402 s时段内共有14个采样点测得的加速度响应等于90 m/s2,17.255 s、17.266 s、17.310~17.315 s、17.368~17.374 s时段内共有15个采样点测得的加速度响应等于-90 m/s2。相邻的数个采样点测得了同样的加速度数据显然不符合客观规律,这预示着在人工地震波1的作用下,测点7的响应在上述时间段内试验数据可能发生错误,或未测量完全。由于整个过程涉及工况较多、试验过程中对试验结构进行了数次更换[6-7],所以试验过程中未能发现这个问题,且试验完成后试验台已被拆除,无法重复进行试验。为了使试验数据可用并达到试验目的,接下来使用神经网络对试验中错误数据进行预测,以补全工况2中测点7的时程曲线。
2 神经网络的构建
2.1 思维进化算法优化BP模型
人工神经网络(ANN,artificial neural network)是在对人脑组织结构和运行机制的认识理解基础之上模拟其结构和智能行为的一种工程系统。现有应用在振动控制计算领域的神经网络主要为反向传播(BP,back propagation)神经网络和遗传算法(GA,genetic algorithm)优化的BP神经网络[8-9]。有学者将GA-BP神经网络用于地震预测中发现,相较于BP神经网络,GA-BP神经网络对地震预测精度有所提高,但遗传算法的交叉与变异算子存在双重性且仍然存在个别数据绝对误差过大的现象,容易陷入局部最小值,这是不利于预测准确性的[10]。在遗传算法的基础上皮骏等[11]用三角函数和高斯变异操作对遗传算法进行了改进,将其应用到航空轴承诊断中,诊断准确率均优于其他网络结构。孙承意等[12]于1999年提出了思维进化算法(MEA,mind evolution algorithm),该算法沿袭了GA的一些基本概念,但同时又具有自己的特点。MEA的趋同和异化操作可以有效消除种群中的劣势种群,并能克服多数进化算法的缺陷,同时避免遗传算法中交叉和变异算子双重性,提高了算法的整体搜索效率,在一定程度上能保证较优的局部预测值和较好的全局预测精度,具备快速收敛能力。Yu等[13]将MEA优化BP神经网络模型应用于热油管道预测模型,相比未优化的BP神经网络模型和GA-BP模型,其预测精度、迭代次数和时间均有较大提升,取得了较好的效果。研究结果表明MEA-BP神经网络预测能力高于BP神经网络。因此研究利用 MEA-BP神经网络对验证组数据进行预测,并与BP神经网络预测结果进行了对比,选用预测误差最小的神经网络及其拓扑结构对缺失数据进行预测。
MEA-BP神经网络实现步骤如下:
(1) 按得分对解空间内所有随机生成的初始个体进行排序;
(2) 在得分最高的个体周围产生新个体并组成群体;
(3) 以各子群体的优胜个体为中心计算个体得分,并进行趋同操作,如此直到得分不再提升则终止,代表子群体已成熟,其中个体得分最高代表群体分值;
(4) 子群体成熟后进行异化替代,从而得到全局得分最高体;
(5) 判断是否可以停止,不满足则重复以上步骤;
(6) 确定神经网络权值阈值为最优个体解码后的值;
(7) 对BP神经网络进行训练。
2.2 神经网络构造
中间层数选取:BP神经网络的非线性映射能力十分强大,最基本的BP神经网络(中间层仅为1层)就可实现任意一个非线性函数的映射。为了改善网络预测精度,降低网络预测误差,可增加中间层层数,但这样做往往会减慢网络收敛速度,增加网络运行时间[14]。综合考量,选择用于预测数据的网络的中间层层数仅为1层。
输入层节点选取:由于振动台试验中分布13个加速度测点,每个测点包含63 877个加速度值,但神经网络的输入节点并不是越多越好,当样本数大到一定程度时,网络的速度也很难再提高[15],训练误差也不会下降,因此利用相关系数法对训练集进行选取,相关系数计算公式为
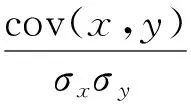
(1)
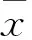
隐含层节点选取:隐含层节点数经验公式为
(2)
其中:l是隐含层节点数;n是输出层节点数;m是输入层节点数;a为[1,10]之间的常数。根据式(2)确定l的取值范围后,利用试凑法确定隐含层节点数:先设置较大的隐含层节点数,然后逐渐减小节点数,用同一样本进行训练,从中确定网络误差最小时对应的节点数。
激活函数的确定:选取S型函数tansig()为隐含层传递函数,由于输出层节点数为1,因此输出层激活函数选择线性函数purelin()。
为了对比BP神经网络、MEA-BP神经网络作为预测加速度数据算法的准确性和适用性,随机选取表1所列工况2中加速度数据测量完整的测点5作为训练组来确定神经网络的拓扑结构。由于测点5中加速度值超过±70 m/s2的数据有33个,接近测点7中错误加速度数据个数,因此选取加速度数据值超过±70 m/s2的33个数据作为被预测数据;工况2加速度数据测量完全的测点9作为验证组,来验证构造出的神经网络的适用性,由于测点9中超±70 m/s2的数据有96个,远远多于测点7中29个未测量到数据,这会影响预测精度,因此选择测点9中数据值超过±80 m/s2的40个数据作为被预测数据。
神经网络预测数据过程为:首先,随机选取测量完全的加速度测点数据训练神经网络,利用试错法确定神经网络的拓扑结构,从较大网络拓扑结构出发,逐步缩小网络结构,以平均绝对误差和均方根误差为准获得最佳预测网络结构;其次,选取另一组测量完全的加速度数据验证组来验证该网络结构的适用性;最后,利用预测精度高的网络结构来预测试验中未测得的数据。工况2中测点5加速度数据与其他测点数据相关系数如表2所列。

表2 工况2测点5与其他测点的相关系数Table 2 The correlation coefficient between measuring point 5 and other measuring points in working condition 2
由表2可知,在工况2中加速度测点4、测点6、地震台面加速度与测点5的相关性较大,均大于0.99。因此,选用测点4、测点6、地震台面加速度值作为神经网络的输入值,按3∶2的比例将全过程加速度数据分为训练集和测试集,并对神经网络进行训练(63 876个采样点)。
由式(2)可知在输入节点为3时,该网络隐含层节点数选取范围为[3,12],训练过程中发现当隐含层节点数为7时,训练次数最少且达到目标精度,因此隐含层节点确定为7。
综上,确定网络结构为3-7-1,分别利用BP神经网络、MEA-BP神经网络对数据进行训练。采用均方根误差(RMSE)和平均绝对误差(MAE)进行预测精度评定,二者的计算公式分别为
(3)
(4)

利用BP神经网络、MEA-BP神经网络在不同输入层节点下对工况2测点5中超±70 m/s2的33个加速度数据进行了预测,预测值与真实值之间的RMSE、MAE比较结果如表3所列。

表3 测点5预测值与真实值之间的误差比较Table 3 Comparison of the error between the predicted value and the true value at the measuring point 5
由表3可知,当输入层节点数为3时,MEA-BP神经网络加速度预测值与真实值之间的MAE为36.156 6,是BP神经网络预测值与真实值MAE的63.82%;RMSE为158.807 6,是BP神经网络的67.78%,误差较大。当输入层节点数分别降到2、1进行网络训练时,发现输入层节点数为1时网络预测精度低于输入层节点数为3时的预测精度,因此研究只给出输入层节点数为2时的预测精度分析。选择与测点5相关系数最大的测点4、测点6作为输入集,利用试凑法确定隐含层为6,对网络进行训练。预测值与真实值之间残差比较如图4所示。

图4 各网络结构残差值对比Fig.4 The residual contrast of different network structure
综合表2和图4可知,当输入节点数为2时,MEA-BP神经网络预测精度优于3层输入的精度,MEA-BP神经网络预测值残差波动范围稳定在1.5 m/s2之内,其中最大残差值为-1.510 4 m/s2,发生在第17.398 s,真实最大加速度值为-77.407 6 m/s2,发生在第13.369 s,对应的预测值为-73.748 2 m/s2,为真实最大加速度值的95.189%。综上可知,输入节点数为2时,MEA-BP神经网络拓扑结构对于加速度数据的预测结果与真实值是基本吻合的。
因此,采用MEA优化的3层BP神经网络对振动数据进行预测,输入节点数为2,隐含层节点数为6,输出层节点数为1。 用于预测加速度数据的神经网络构造流程如图5所示。
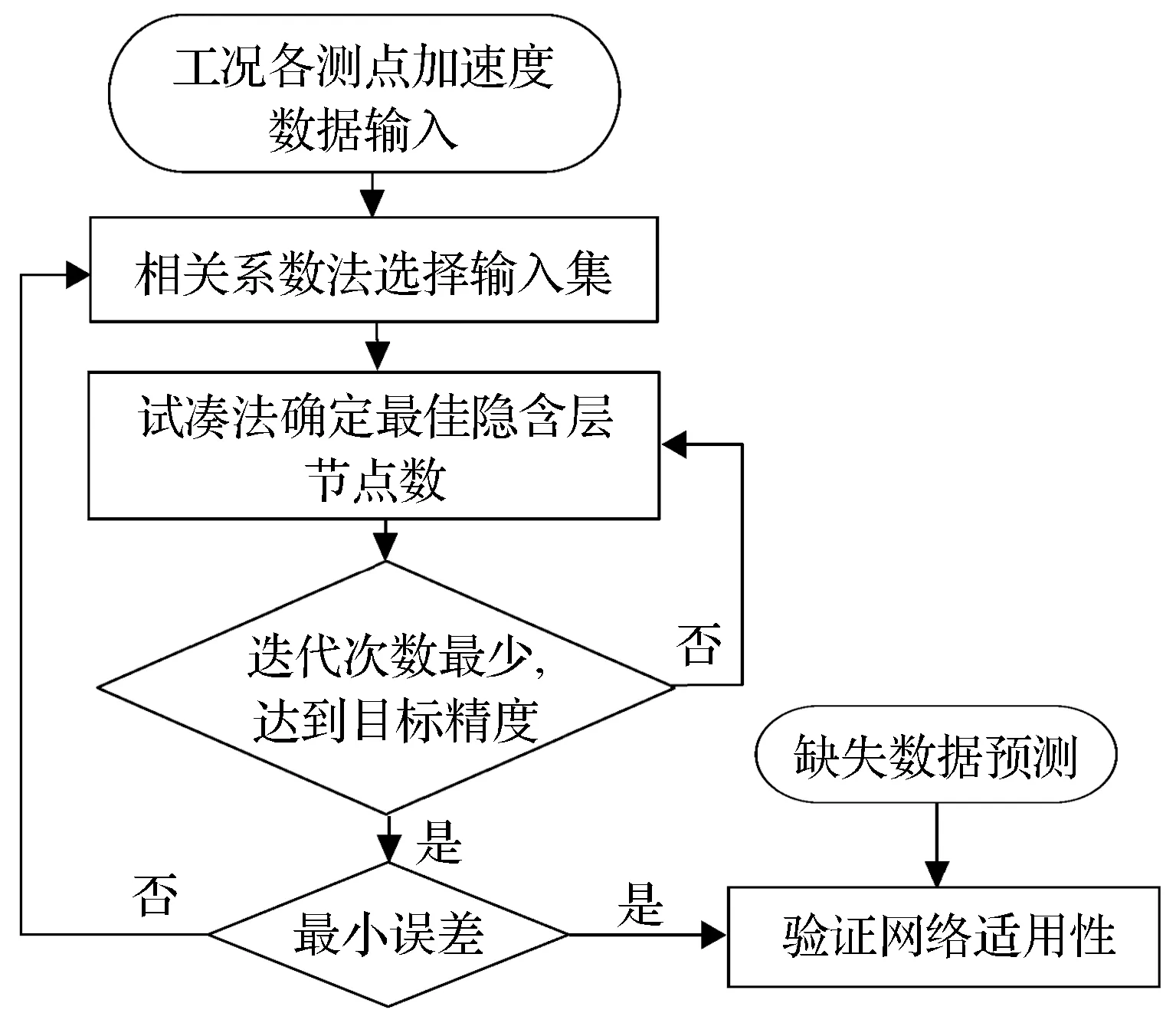
图5 神经网络加速度数据预测流程Fig.5 Flow chart of neural network acceleration data prediction
网络训练完成后还需要验证其适用性。选取同一工况下即工况2加速度测点9作为验证组,其中超过±80 m/s2的40个数据作为被预测数据,利用上述训练好的神经网络拓扑结构进行预测。工况2中测点9与其他测点相关系数如表4所列。

表4 工况2测点9与各测点的相关系数Table 4 The correlation coefficient between measuring point 9 and other measuring points in working condition 2
由表4可知,工况2中测点8、测点10与测点9数据相关系数最高且均大于0.99,因此,训练集选取测点8、测点10作为上述得出的网络拓扑结构的输入集。测点9预测值与真实值之间残差值如图6所示。
由图6可知,测点9的40个预测数据中,预测值与真实值最大残差为1.708 17 m/s2,发生在第17.226 s。预测值与真实值之间的MAE为0.438,RMSE为3.765,误差在可接受范围内。因此,上文所训练MEA-BP神经网络拓扑结构对于加速度数据的预测具有适用性,可以用来预测试验中超出加速度测量计量程的29个数据。
3 未测得数据预测结果
在工况2测点7的加速度响应时程数中有15个数据值为90 m/s2,14个数据值为-90 m/s2。利用前述训练并验证后的神经网络拓扑结构对这29个未测得数据进行预测。
利用相关系数法对预测该测点的神经网络训练集进行选取,工况2中其他各测点与测点7相关系数如表5所列,选取与测点7相关系数大于0.99的测点6、测点8作为输入集。利用训练后的网络对测点7响应时程中未测得数据进行预测,结果如表6所列。

表6 工况2测点7未测得数据预测值Table 6 The unmeasured predicted value at measuring point 7 in working condition 2
由表6可知,预测结果中第17.257 s的响应小于90 m/s2,这说明预测结果具有一定的误差,但在前述中已经验证,该神经网络误差在可接受范围内。由表6还可以看出,在人工地震波1的激励下管道结构测点7的最大响应为97.667 m/s2,出现在第17.343 s。补全后工况2测点7的加速度时程曲线和局部放大图如图7所示。
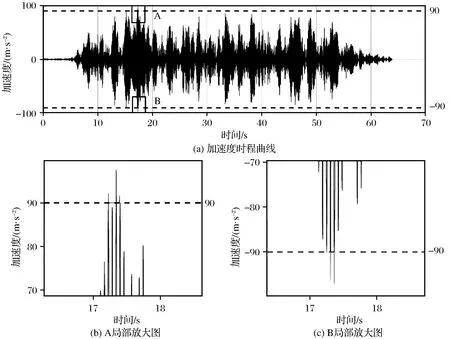
图7 补全后工况2测点7的加速度时程曲线和局部放大图Fig.7 Time curve and local enlarged view of the acceleration of measuring point 7 after completion in working condition 2
4 结论
由于已经完成的管道系统地震台模拟试验不具备可重复性,利用MEA-BP神经网络对管道系统由于加速度测量计损坏导致的响应最大位置缺失的29个加速度数据进行了预测,补全了该测点的加速度响应时程曲线,提高了试验数据的利用率,避免了试验经费的浪费,保证了试验目的的顺利达成。
研究结果表明了MEA-BP神经网络在预测超量程地震响应数据方面的可行性,为补全缺失的振动数据提供了新的途径;而且经过算例分析证明了MEA-BP神经网络在结构响应的预测中精度高于BP神经网络。
