深水变梯度钻井井筒压力预测模型的研究
2023-01-03张锐尧李军柳贡慧
张锐尧,李军, ,柳贡慧,
1 中国石油大学(北京)石油工程学院,北京 102200
2 中国石油大学(克拉玛依)石油工程学院,克拉玛依 840000
3 北京工业大学,北京 100022
0 引言
2019年我国原油进口量突破5亿t,对外依存度逐年升高[1-3]。所以亟需进一步提升我国油气钻采技术,增加油气生产总量,从而减少对外依存度。我国海域内蕴藏着丰富的油气资源,近年来深水油气资源已经逐渐发展为我国油气勘探开发的重要接替区[4-6]。但是深水地质环境复杂,存在地层高温与海水低温的特殊温度场环境以及浅部地层弱胶结、易坍塌的特点[7-8],并且在深水钻井中,地层的孔隙压力较高,破裂压力低,最终形成了窄压力窗口的特征,使得井筒压力控制的难度加大[9]。而注空心球变梯度钻井方法在应对该难题方面具有较大的发展前景。
2003年国外Maurer[10]公司最早在一项专利中提出多梯度钻井的思想,该钻井方式实现的关键在于安装井下特殊装置,目的是用来分离钻井液中的轻质空心球,并将其注入环空。2007年,殷志明等[11]设计了切向入口式旋流分离器,然后基于空心球与钻井液的密度差,并利用旋流分离器的离心力,实现了对空心球的分离。2012年,殷志明[12]等人对井下空心球分离注入装置进行仿真分析,并建立了井筒压力分布模型。结果表明采用空心球分离注入装置可以对井筒压力进行优化分配,从而使得环空压力剖面线处在密度窗口范围内。2016年,廖超[13]对井下旋流分离器进行了设计,在保留原有的切向入口的条件下,在分离器的轴线处增加导流管。通过导流管将部分钻井液引入旋流腔进行分离,并通过数值模拟对分离器的分离效率进行了验证,但总体分离器效率仅为40%,且缺乏相应的室内试验对其进一步验证。2019年,王江帅等[14]建立了基于井下分离的双梯度钻井井底压差计算模型,并对钻井关键参数进行了优化设计,实现了对最大钻进深度的预测。但是文章中所提到的分离器的分离效率最高也只有40%,在实际钻井过程中很难实现双密度梯度的目的,并且文中没有对双梯度/多梯度钻井条件下的井筒压力模型进行相关的研究。
本文针对目前注空心球变梯度钻井中分离器分离效率不高的技术瓶颈,研制了过滤分离器,通过数值模拟和室内试验对其分离效率进行了研究,验证了其有效性与可行性。建立了变梯度钻井井筒压力预测的数学模型,基于钻井数据进行了数值计算,同时对不同影响因素条件下的井筒压力进行了敏感性分析。该研究可以为深水变梯度钻井提供理论与技术参考,使其能够更好地适用于窄压力窗口条件下的安全钻井。
1 过滤分离器及其分离效率的研究
因为井下分离器的分离效率对变梯度钻井方式的可行性具有直接的影响。所以该部分首先介绍了所研制的过滤分离器的流场结构以及工作原理;然后通过数值模拟和室内试验相结合,验证了过滤分离器可以实现高效分离的可行性与有效性。
1.1 工作原理
如图1所示,过滤分离器由上、下接头、工具外筒,第一、二级流道、过滤结构(含球形过滤塞和金属过滤网)、套筒组成。其中金属过滤网直接贴合在球形过滤塞的球形外表面,然后通过螺栓将过滤结构与第三级外筒的端面进行固定。套筒上开有三个呈圆周等距分布的通孔使得分离口与环空相通。而球形过滤塞上开有呈圆周等距分布的20 mm通孔,如图1所示,可以保证钻井液顺利进入下部钻柱,而不影响正常钻进。在钻井过程中,分离器通过上、下接头与钻柱连接。空心球与钻井液混合均匀后通过上部钻柱注入,当混合流体进入过滤分离器后,在过滤结构处实现对空心球的分离。因为空心球的尺寸范围一般为0.2~1 mm,而金属过滤网的孔径尺寸小于空心球对的直径,根据过滤分离的原理可知[15],空心球无法通过金属过滤网而被过滤分离。如果要实现多点分离的目的,则可以为不同分离器安装不同孔径尺寸的金属过滤网,且从上部钻柱到下部钻柱的方向,所安装的金属过滤网的孔径尺寸逐级减小。而使用的空心球则依据金属过滤网的尺寸,进行多个直径尺寸的匹配。则钻井液中的空心球会被过滤分离器从大到小逐级过滤。而过滤出的空心球会短暂停留在金属过滤网的球形面上,由于球形面的阻力小,并且有钻井液的不断冲刷作用,所以被分离出的空心球会在部分钻井液的携带下由球形面经过分离口,顺利进入到环空中,而不会引起过滤网的堵塞。如果以过滤分离器为参考,因为空心球的密度比钻井液的密度小,所以上部环空中为低密度的混合流体(轻质流体),而下部环空中为原钻井液(相对于轻质流体,可以称为重质流体),从而在上、下环空中形成了2个或多个密度梯度。
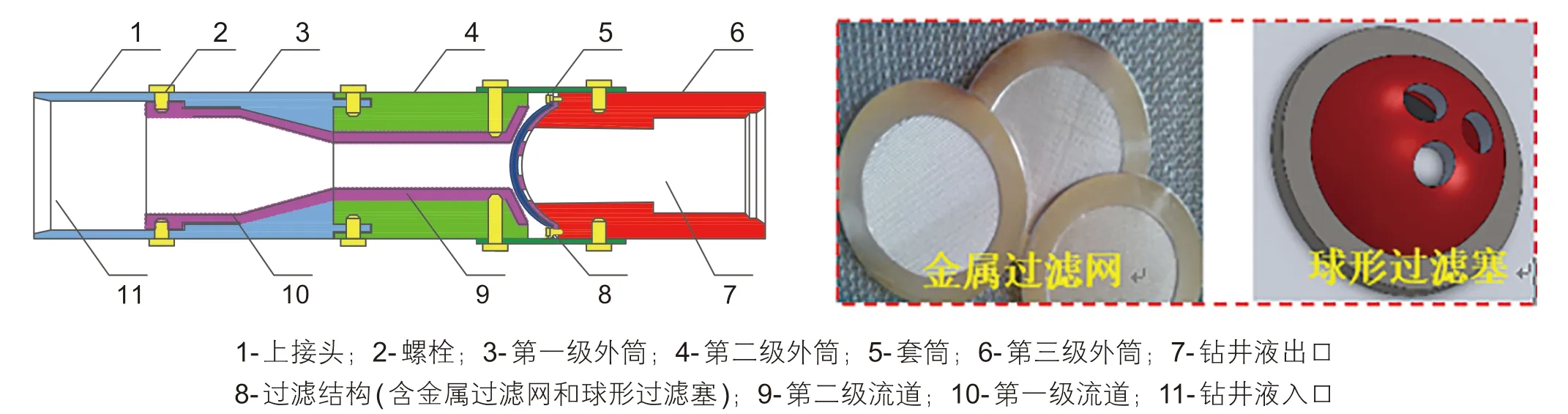
图1 过滤分离器二维结构Fig. 1 Two-dimensional structure of the filter separator
1.2 分离效率的数值模拟
过滤分离器对空心球的分离原理类似于滤纸、孔板等多孔介质的过滤过程[16],过滤分离器分离效率的高低,关键在于过滤结构能否实现对空心球的过滤分离。本文利用多孔介质模型来模拟过滤结构的过滤机理,并引入欧拉多相流模型来模拟空心球与钻井液的混合流动。通过耦合上述两个模型,最终计算得到了不同注入速度和空心球体积分数条件下的分离效率。如图2~图5所示,当注入速率一定时,随着空心球体积分数的增加,分离效率逐渐增加;而当空心球体积分数一定时,随着注入速度的增加,分离效率同样逐渐增加。其中分离效率的变化范围为96.5%~98.7%之间。与体积分数的影响相比较,排量对分离效率的影响轻工更显著。因为空心球体积分数的增加,会增加球—球接触面积,从而减小了空心球与钻井液的接触面积,最终减小了钻井液的曳力,有利于对空心球的过滤分离;而排量的增加会直接增大对空心球的冲刷作用,对分离效率的提升有显著的影响。
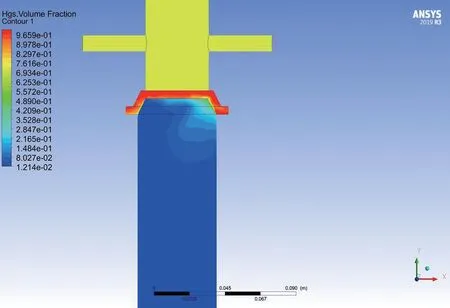
图2 入口速度为0.5 m/s,体积分数为10%时的分离效率Fig. 2 The separation efficiency when inlet velocity is 0.5 m/s and the volume fraction is 10%
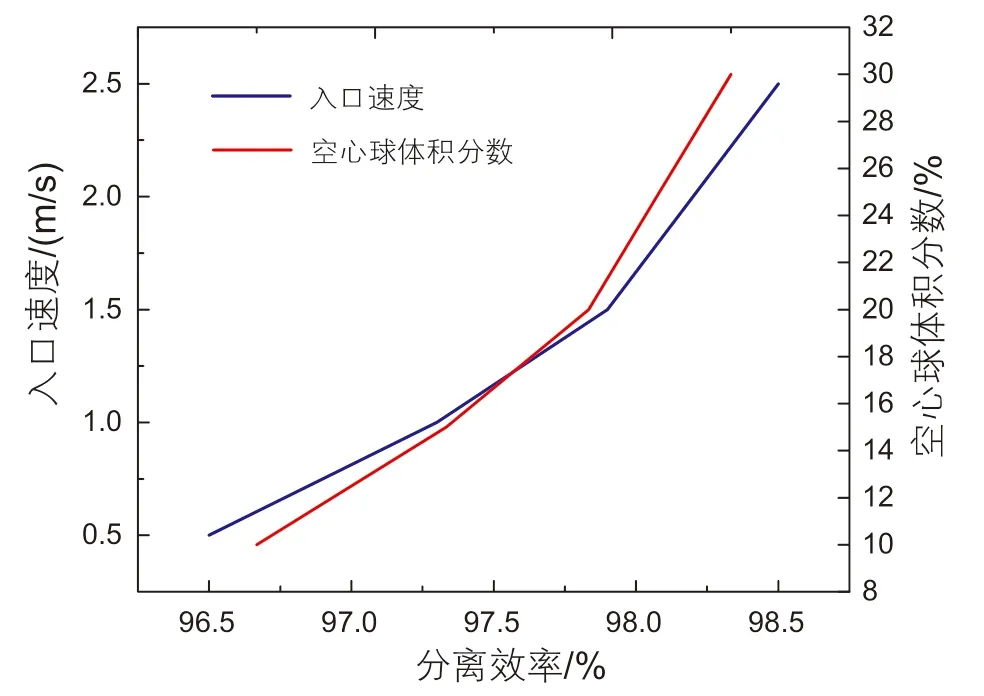
图5 不同入口速度或体积分数时的分离效率Fig.5 The separation efficiency at the condition of different inlet velocity or volume fraction
1.3 分离效率的试验研究
1.3.1 试验原理
如图6所示,为双梯度钻井室内模拟试验系统,主要包括控制柜(含软件界面与控制器)、模拟钻柱与环空,过滤分离器短节、液压泵、注入与排出管线、气阀、搅拌池与储集池等。控制柜主要用于调节液压泵的排量以及气阀的开关。该过滤分离器为室内试验模拟样机,因为该试验的关键是研究过滤分离器的分离效率,所以不考虑井下温度以及压力对过滤分离器的强度的影响。试验过程中将过滤分离器与模拟钻柱连接,上部入口与注入管线相连;过滤分离器的分离口与返回管线相连;模拟钻柱的底部与储集池相连。

图6 双梯度钻井模拟循环系统 Fig. 6 Simulation system of dual-gradient drilling
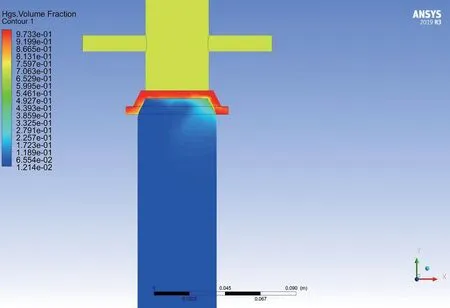
图3 入口速度为1.5 m/s,体积分数为15%时的分离效率Fig. 3 The separation efficiency when inlet velocity is 1.5 m/s and the volume fraction is 15%
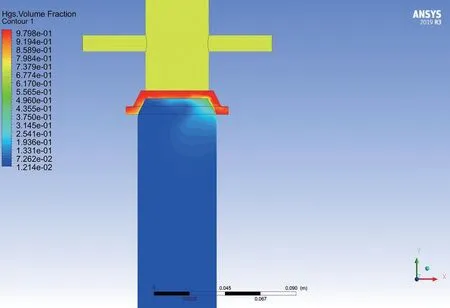
图4 入口速度为2.5 m/s,体积分数为20%时的分离效率Fig. 4 The separation efficiency when inlet velocity is 2.5 m/s and volume fraction is 20%
室内循环试验的工作原理如图7所示。该试验在室温条件下展开,试验选用的钻井液为深水抗高温纯水基钻井液体系,其在低温—高温变化环境中仍能保持良好的流变性能。先将钻井液与空心球在搅拌池中混合均匀,然后开启阀门1、2、3、4,并启动液压泵。当流体进入过滤分离器后,空心球会被分离并从分离口经过返回管线进入到储集池1中。因为在储集池1的入口处安装有过滤网,所以可以将分离的空心球进行收集与干燥称重。而其余钻井液则通过分离器后进入到下部钻柱,最后流入储集池2中。当循环结束后,关闭阀门3和4,对比分离的空心球与注入空心球的重量,即可得到该条件下的分离效率。然后将回收的空心球注入搅拌池中循环利用,并继续调节泵的排量或改变注入的空心球的体积分数、直径以及密度等,重复上述试验过程。这样就可以利用该循环系统得到不同条件下的过滤分离器的分离效率,最终的试验结果如图8所示。

图7 分离效率实验的工作原理Fig.7 working principle of separation efficiency experiment

图8 分离效率的实验结果Fig. 8 Experimental results of separation efficiency
1.3.2 结果分析
如图8(a)所示,随着泵排量与空心球的体积分数的不断增加,分离器的分离效率先缓慢增加,然后急剧上升,最后达到98.5%左右后趋于稳定。因为随着排量的不断增加,过滤出的空心球在过滤结构处(金属过滤网的球形面)受到的冲刷作用更强,更有利于空心球进入环空中;而空心球体积分数的增加,使得空心球含量增加,减小了空心球与钻井液的接触面积,从而减小了钻井液对空心球的曳力,有助于空心球顺利进入环空中。又因为钻井液黏度的影响,空心球存在一定的聚集和粘附,导致空心球在循环系统中会有部分损失,所以当分离效率达到98.5%后,不再随排量和空心球体积分数的增加而增加。如图(b)所示,分离效率随着空心球直径的增加而增加,随着密度的增加而减小。因为随着直径的增加,空心球与钻井液的接触面积增加,受到的冲刷作用更大,所以分离效率增加;而相同体积的空心球,随着密度的增加,质量逐渐增加,则需要的冲刷力更大,钻井液将其携带进入环空会更困难,所以分离效率降低。
综合数值模拟和室内试验结果可知,过滤分离器在不同钻井液排量、空心球体积分数以及不同直径和密度的条件下,分离效率的变化区间为95%~98.7%。并且在试验过程中,因为钻井液黏度的影响,少部分空心球出现聚集和附着现象,但是基本实现了全部过滤分离,也没有观察到滤网堵塞现象。如果不考虑试验的误差影响,则一定程度上验证了过滤分离器的有效性和可行性。
2 变梯度钻井井筒压力的预测模型
基于对过滤分离器的分离效率的研究结果,分别建立了双梯度和多梯度钻井条件下的井筒压力预测模型。然后在温压耦合条件下,结合钻井数据进行了数值模拟研究和敏感性分析。
2.1 双梯度钻井井筒压力的预测模型
在钻井循环过程中,环空中紊流状态时的压降计算如式(1)所示[17-19],并代入范宁摩阻系数,可以得到分离器上部环空中轻质流体的压降以及下部环空中的重质流体的压降,分别如式(2)、(3)所示:
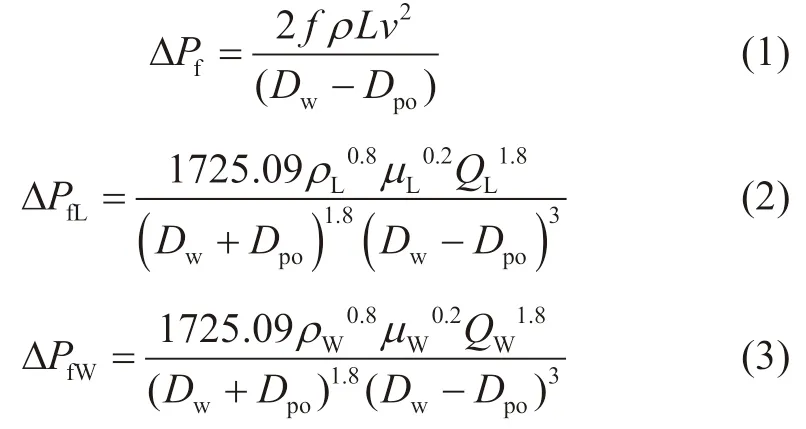
如图9所示为双梯度钻井循环过程中,过滤分离器处于3种不同位置时的钻进状态,分别对3种状态标记为状态A、B、C。并选择环空中某一深度处的任意点,对其在3种状态下的井筒压力进行分析。假设空心球注入的体积分数为ε,过滤分离器对空心球的分离效率为ψ,故而可以得到分离器上、下两部分环空中的轻质钻井液与重质钻井液的密度与黏度,分别如式(4)和(5)所示,对应的两段液柱的高度如式(6)所示:

图9 双梯度钻井井筒压力预测物理模型Fig. 9 Physical model of wellbore pressure prediction of dual-gradient drilling

(1)对于状态A的任意点T的压力计算:
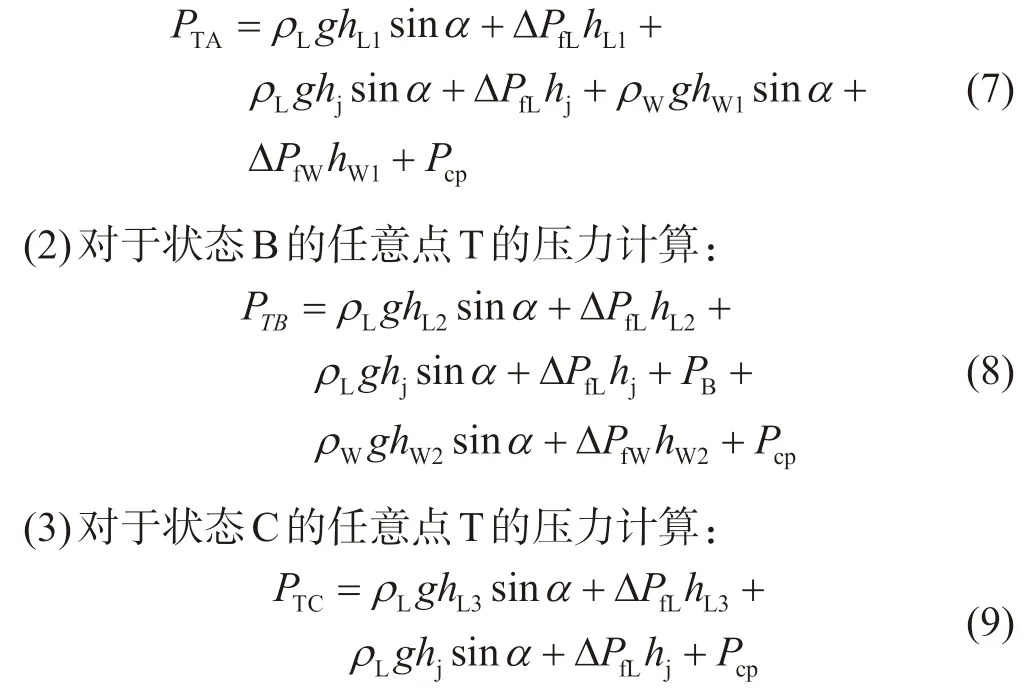
综合上述情况,可以得到随钻井底压力预测的数学模型如式(10)所示:

式中ρ为环空中流体密度,kg/m3;ε为空心球体积分数,%;ψ分离效率,%;μ为环空中流体的黏度,mPa·s;hL为上部环空的液柱长度,m;hj为分离器段液柱长度,m;hW为下部环空中液柱的长度,m;hT为目标点深度,m;H为井深,m;脚标1、2、3为不同钻井状态;脚标L、W分别代表分离器上部环空与下部环空的液柱;Hs-b*为分离器底部距离钻头的距离,m;α为井斜角,°;PT为环空中目标点的压力,MPa; Pcp为回压,MPa;Pdh*为随钻井底压力,MPa;L*为实时井深,m;g为重力加速度,9.8m/s2;
2.2 多梯度钻井井筒压力预测模型
如图10所示为基于两个分离器的多梯度钻井井筒压力预测物理模型,根据分离器的位置为参考,将环空划分为不同段,不同环空段的钻井液分别称为轻质钻井液-1、轻质钻井液-2以及重质钻井液,其对应的混合流体的初始密度式(11)和(12)所示:

图10 多梯度钻井井筒压力预测的物理模型Fig. 10 Physical model of wellbore pressure prediction of multi-gradient drilling
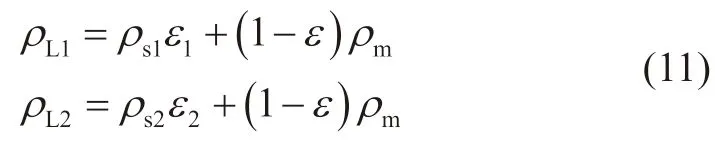
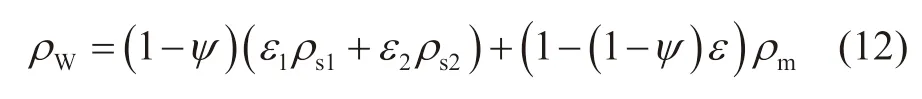
从而可以得到在钻进过程中,不同目标点位置处的压力,分别选择A、B、C 3种状态进行分析,得到对应目标点处的井筒压力,如式(13)~(15)所示:
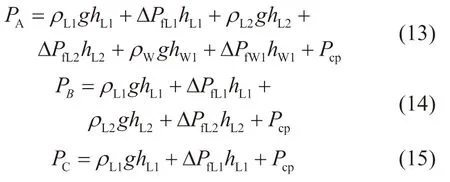
综合上述情况,可以进一步地推导得到随钻井底压力的预测模型如式(16)所示:
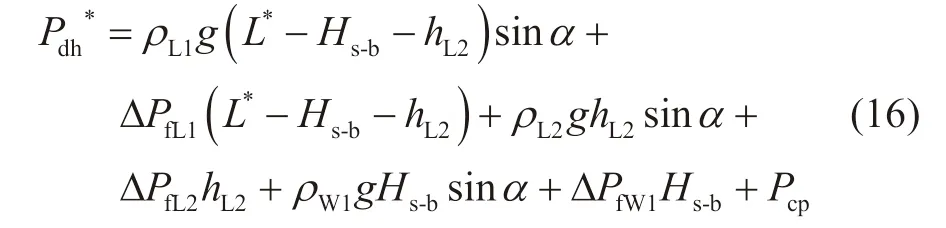
式中ρ为环空中流体密度,kg/m3;ε为总的空心球体积分数,%;ε1、ε2分别为两级分离器分离出的空心球体积分数,%;ψ分离效率,%;μ为环空中流体的黏度,mPa·s;hL为上部环空的液柱长度,m;hj为分离器段的液柱长度,m;hW为下部环空中的液柱长度,m;hT为目标点深度,m;H为井深,m;脚标1、2、3为不同钻井状态;Hs-b为分离器底部距离钻头的距离,m;α为井斜角,°;PT为环空中目标点的压力,MPa;Pcp为回压,MPa;Pdh*为随钻井底压力,MPa;L*为实时井深,m;g为重力加速度,9.8 m/s2。脚标:L1、L2、W分别代表两级分离器上部环空与下部环空的液柱;s1、s2为两者不同尺寸的空心球,mm;m代表钻井液。ΔPf为环空压降,MPa。
2.3 辅助方程
因为在钻井循环过程中,钻井液的热物性参数与温度、压力之间相互影响,所以本文利用多元非线性回归分析方法对 McMordie等[20]的水基钻井液试验数据进行处理,得到钻井液的密度与黏度随温度、压力变化的关系式为:
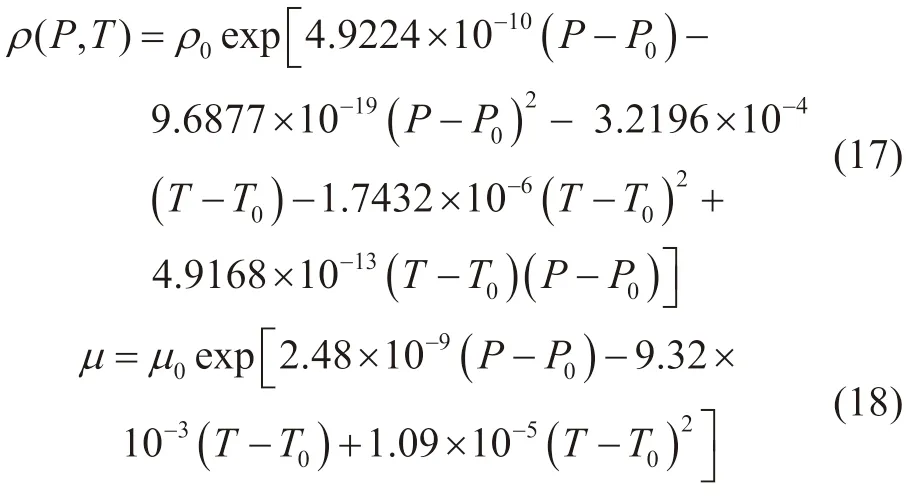
式中ρ为混合流体随温度和压力变化的密度,kg/m3;ρ0为常温条件下混合流体的初始密度,kg/m3;T0为常温,℃;P为压力,MPa;T为温度,℃;μ为混合流体随温度和压力变化的黏度,mPa·s;μ0为常温条件下混合流体的黏度,mPa·s。
3 算例分析
3.1 基本数据
根据上述建立的变梯度钻井井筒压力预测模型,并考虑井筒温度和压力对流体物性参数的影响,再结合南海某区块的钻井数据进行数值计算和敏感性分析。其中部分数据如下[21-23]:水深1500 m,入口温度为15 ℃,地表温度为20 ℃,混合流体的初始排量10 m3/h,地温梯度为0.25 ℃,钻井液初始密度为1200 kg/m3,比热为3900 J/(kg·K),导热系数为1.73 W/(m·K),海水密度为1050 kg/m3,比热为4130 J/(kg·K),导热系数为0.65,空心球密度为600 kg/m3,比热为750 J/( kg·K),导热系数为0.47 W/(m·K),选择过滤分离器的分离效率为98%。
根据上述数据,首先对常规钻井(单梯度)、双梯度和多梯度钻井条件下的环空压力进行了计算,如图11所示。与常规钻井相比,在相同井深位置处,变梯度钻井井筒压力要小于常规钻井;由于以分离器为参考点,上部环空为低密度的轻质流体,而下部为重质流体,所以在分离器位置处环空压力存在明显的拐点,环空压力分布曲线由原来的单一线性分布变为折线分布;并且随着分离器数量的增加,环空压力分布曲线上的拐点数量也相应增加,压力分布曲线的弯折程度更大,相同井深位置处环空压力更小,并且拐点位置与分离器的位置相同。
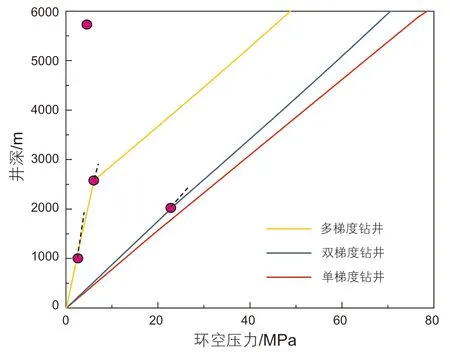
图11 常规钻井与变梯度钻井井筒压力的对比Fig. 11 Comparison of wellbore pressure between conventional drilling and variable gradient drilling
3.2 敏感性分析
3.2.1 双梯度钻井井筒压力的关键影响因素分析
如图12所示,与常规钻井相比,双梯度钻井中上部环空为低密度的混合流体,下部基本为原钻井液,所以在相同井深处,双梯度钻井井筒压力要小于常规钻井。并且因为上、下环空流体存在密度差,从而导致在分离器位置处环空压力存在明显的拐点,其压力分布呈折线分布。在双梯度钻井中,若考虑温度的影响时,下部环空中钻井液受到地层高温的影响,其密度会减小,使得下部环空中的压力比不考虑温度影响时更小。随着钻井液逐渐上返,温度逐渐降低,所以环空压力受到的影响程度逐渐减弱。由图13可知,随着钻井液排量的增加,环空中的压耗则逐渐增大,所以相同井深处的环空压力逐渐增加,但环空压力分布的形态仍然为折线。而当其它条件不变时,随着注入的空心球体积分数的不断增加,如图14所示,相同井深位置处环空压力会不断减小,且环空压力在分离器位置处同样存在明显的拐点。因为随着空心球体积分数的不断增加,从分离器位置往上的环空中,轻质流体的密度逐渐降低,从而导致相同井深位置处,环空压力逐级降低。如图15所示,随着分离器距离井口的位置不断增加,环空压力的拐点位置逐渐下移,则轻质钻井液的液柱长度逐渐增加,而重质钻井液的液柱长度逐渐减小,从而使得环空压力逐渐减小。如图16和17所示,随着空心球密度和钻井液密度的增加,相同井深位置处环空压力逐渐增加。因为随着空心球密度或者钻井液密度增加,则导致轻质段混合流体的密度以及重质段的流体密度都增加,从而使得环空压力增加。并且随着空心球密度的增加,上、下环空流体密度差减小,上、下环空压力分布曲线的斜率差逐渐减小;而随着钻井液密度的逐渐增加,斜率差的变化规律刚好相反。
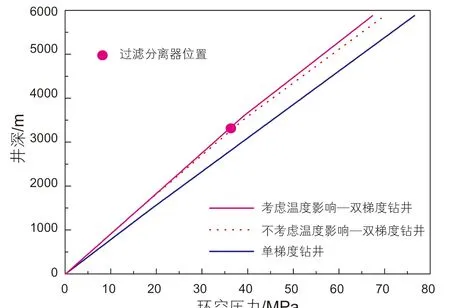
图12 传统钻井与双梯度钻井的对比Fig. 12 Comparison of traditional drilling and dual gradient drilling
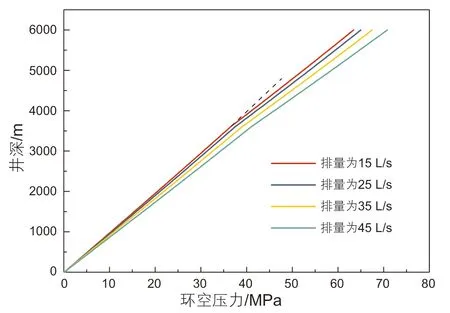
图13 不同排量时环空压力的变化Fig. 13 Variation in annulus pressure under different pump flow rate

图14 不同空心球体积分数时的环空压力Fig. 14 Annulus pressure variation at different volume fractions of HGS

图15 分离器位于不同位置时环空压力的变化Fig.15 Annulus pressure variation when the separator is in different positions
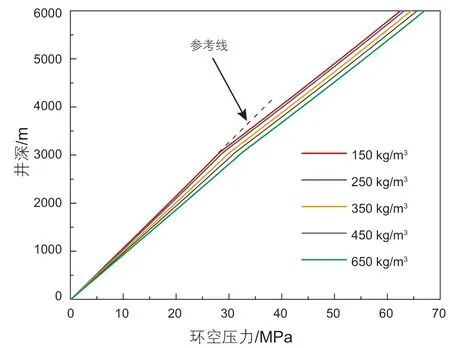
图16 空心球密度对环空压力的影响Fig. 16 The effect of HGS density on annulus pressure
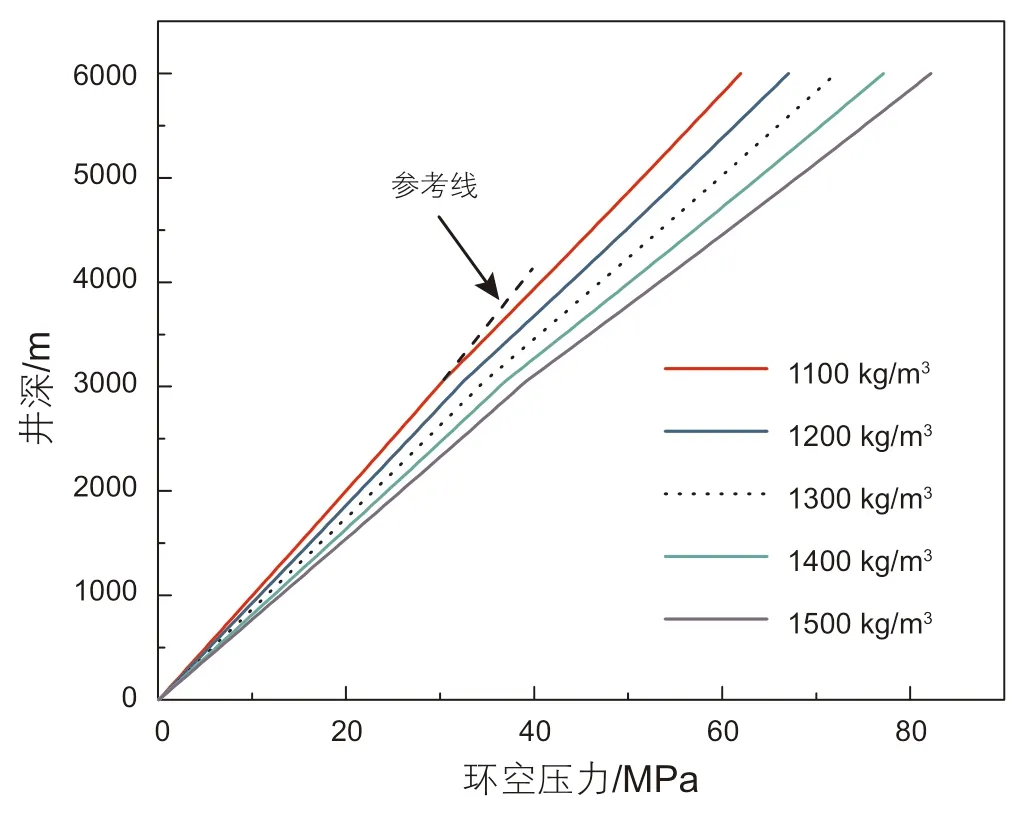
图17 钻井液密度对环空压力的影响Fig. 17 The effect of drilling fluid density on annulus pressure
3.2.2 多梯度钻井井筒压力的关键影响因素分析
如图18所示,随着排量的增加,环空压力逐渐增加。因为随着排量的增加,环空压耗逐渐增加,所以相同井深位置处环空压力逐渐增加。与双梯度钻井相比,多梯度钻井条件下,因为存在多个分离器,所以环空压力分布存在多个拐点,相同排量条件下,环空压力分布曲线的弯折程度更大。如图19所示,随着两个分离器距离井口的位置不断增加,环空压力逐渐减小。因为随着分离器位置的下移,上部环空中轻质流体的液柱长度会逐渐增加,而重质流体段的液柱长度会逐渐减小,从而使得相同井深处的环空压力减小。并且随着分离器位置的不断下移,由于上、下环空中流体的密度差没有发生变化,所以压力分布曲线的斜率差保持不变。如图20所示,随着钻井液密度的增加,环空压力逐渐增加。因为随着钻井液密度的逐渐增加,上、下环空中的流体密度都逐渐增加,但是下部环空中流体密度增加的程度显著大于上部环空。所以与双梯度钻井相比,以分离器位置为参考点,上、下环空压力分布曲线的斜率差会显著增加。如图21所示,随着两级分离器注入的空心球体积分数逐渐增加,环空压力逐渐减小。因为随着空心球体积分数的增加,轻质段流体的密度逐渐减小,而重质段流体密度基本保持不变,从而使得相同井深处环空压力逐渐减小。并且与双梯度钻井相比,相同空心球体积分数条件下,多梯度钻井环空压力更小。因为在体积分数相同的情况下,多梯度钻井含有多级分离器,所以上部环空中轻质流体的液柱长度更长,重质流体的液柱长度更短,从而导致后者的环空压力更低。由于分离器数量增加,使得环空压力分布的拐点增加,曲线的弯折程度更大,所以上、下环空压力分布曲线的斜率差逐渐增加。
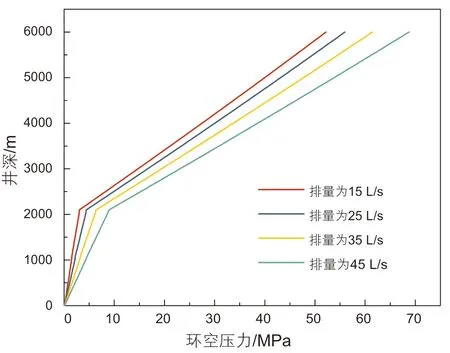
图18 排量对环空压力的影响Fig. 18 Effect of different displacements on annulus pressure

图19 分离器位置对环空压力的影响Fig. 19 The effect of the separators position on annulus pressure
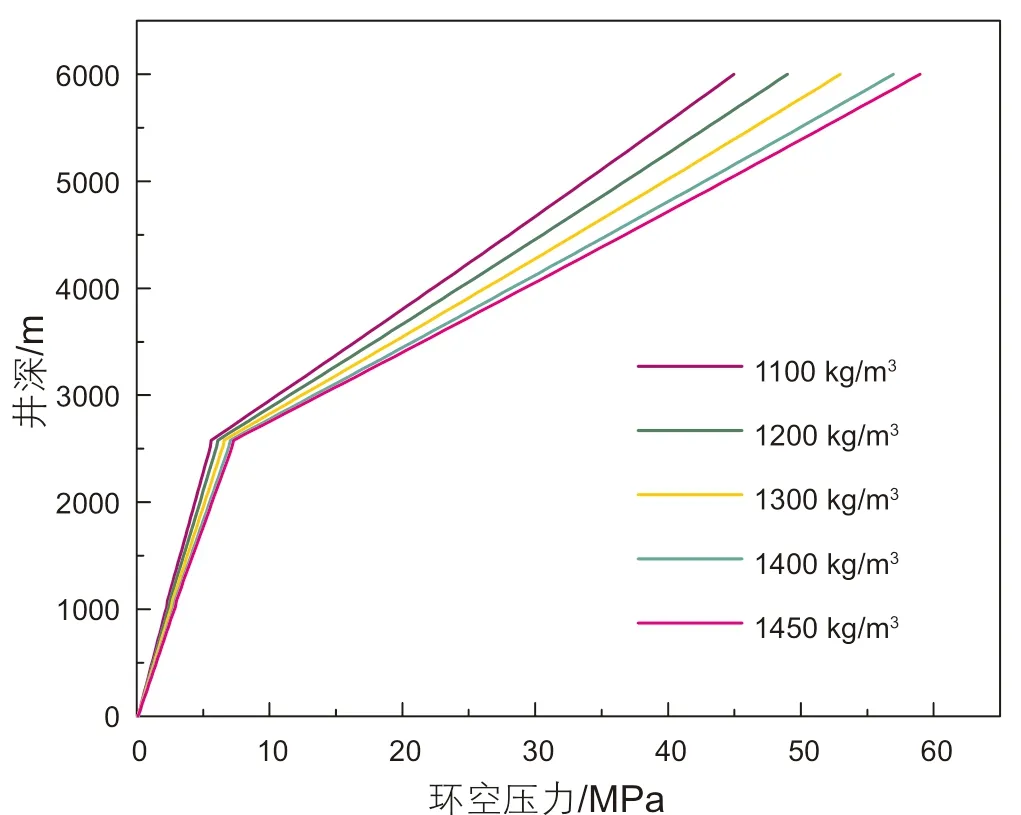
图20 钻井液密度对环空压力的影响Fig. 20 The effect of drilling fluid density on annulus pressure
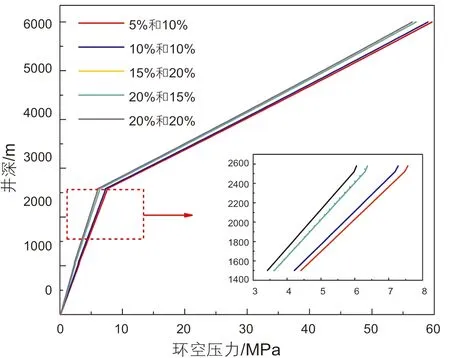
图21 空心球体积分数对环空压力的影响Fig. 21 The effect of HGS volume fraction on annulus pressure
4 结论
本文首先对研制的过滤分离器的总体结构和工作原理进行了介绍,然后利用数值模拟和室内模拟试验验证了其对空心球高效分离的特性。对变梯度钻井井筒压力预测模型进行求解和敏感性分析,得到如下结论:
(1)新型井下过滤分离器可以显著提升分离效率,其分离效率与空心球体积分数、直径和排量呈正相关,最高分离效率可以达到98.5%。该过滤分离器显著提升了变梯度钻井方式的可行性。
(2)与传统钻井相比,在变梯度钻井条件下,环空压力分布曲线上存在明显的拐点,并且拐点的位置和数量与分离器的位置和数量相同。随着分离器数量增加,上、下环空压力分布曲线的斜率差更大,曲线弯折程度更大。
(3)分离器位置和数量、空心球密度和体积分数等关键参数对变梯度钻井井筒压力都有显著影响,所以在钻井参数设计时需要对以上参数进行优化设计。
