随钻伽马成像测井快速正演方法及数值模拟*

吕 伟，张 龙，宋殿光，冯思恒，周 俊

(1.四川天石和创科技有限公司 四川 成都 610091； 2.中石油川庆钻探工程有限公司钻采工程技术研究院 四川 广汉 618300)

0 引 言

随钻地质导向技术在当今水平井施工中，特别是在复杂油藏水平井施工中得到了广泛的应用，并在提高油层钻遇率及采收率方面发挥着越来越重要的作用。该技术通过井下传感器测量的地质及工程参数实时识别地下构造及属性信息，不断修正导向模型及井轨迹[1-3]，指导钻头顺利中靶及最大限度地在目的层中钻进。

随钻伽马成像测井因其测量信息具有方位性，能实现沿井周的扫描成像，精细地描述地层构造，在地质导向作业中得到越来越多的应用[4-6]。该类仪器能准确识别仪器与地层的位置关系，以及仪器相对地层界面的钻进方向，并能有效识别仪器所钻地层处的构造及属性信息，进而帮助地质导向师及时修正地质导向模型及调整井眼轨迹，提升油气储层钻遇率。

为方便掌握随钻伽马成像测井的响应特征，提升该类仪器在地质导向应用中的效果，有必要对其在水平井中的响应特征进行正演模拟。目前对伽马测井响应正演模拟多采用蒙特卡罗方法[7-8]，但该方法计算量大，速度慢，尤其是模拟伽马成像测井，需要的计算量更大，无法满足地质导向作业的实时性要求。为实现快速正演计算，前人在正演模型简化方面做了很多工作，如通过将探测区域简化成圆形[9]、球形[10]或锥形体[11-13]等，实现自然伽马和方位伽马测井的快速正演计算，但少见有伽马成像测井快速正演计算方面的工作。本文在前人研究基础上，开发了一种伽马成像测井快速正演计算方法，并通过对几种典型模型的数值模拟，分析了伽马成像测井响应的特征规律。

1 快速正演方法

1.1 地层模型简化

通常情况下，局部地层为多层水平层状结构，由于伽马仪器的探测深度有限，可将多层地层模型简化成三层地层，即仪器所在层以及上下围岩，如图1所示。

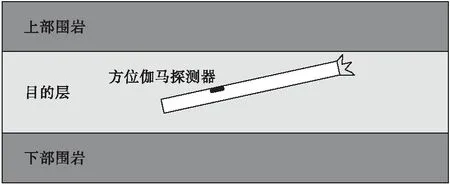
图1 三层地层模型

1.2 正演模型

伽马成像正演模型如图2所示。将探测器的探测范围定义为锥形体范围，根据地层界面与探测区域的相交关系，可得到围岩与目的层各自对探测器响应的贡献，将两者的贡献合成后，即得到探测器的总响应。

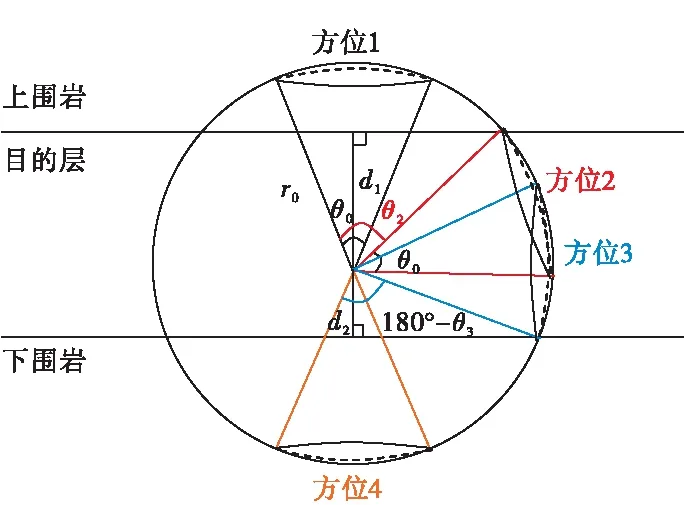
图2 成像正演模型

图中方位1和方位4分别对应仪器的0°和180°方位，即正上方和正下方所对应的方位，方位2和方位3对应的方位分别为θ2和θ3，θ2和θ3这两个方位之间的伽马响应均为纯目的层响应。分别得到这4个位置的响应后，再通过插值计算，可得到0°到180°之间所有方位的响应值。很明显，180°到360°和0°到180°之间的方位响应是对称的，因此，只需求取0°到180°的方位响应即可。图2给出的是探测区域与上下围岩都相交的情况，当只与一个围岩相交时，做对应简化即可。

1.3 正演算法

图2中所示的4个方位中，方位2和3为纯目的层的伽马响应，方位1和4的计算方法相同。因此，下面仅给出方位1的响应计算方法。

方位1处的锥形探测区域与地层相交可以分两种情况考虑，如图3所示。

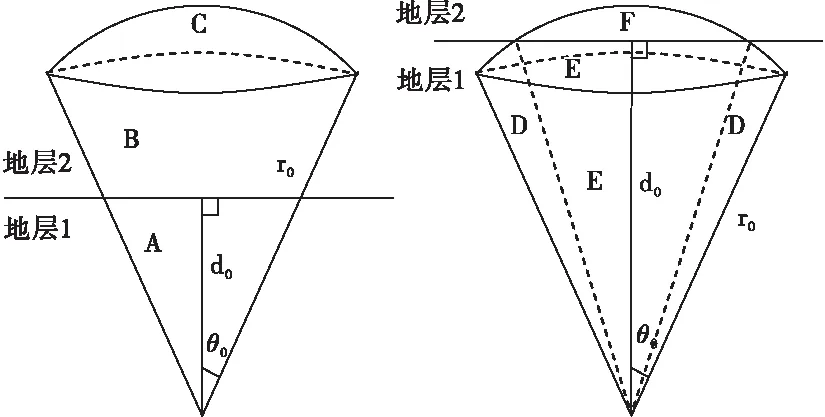
图3 锥形探测区域与地层相交情况

当探测器探测范围内不受邻层影响时，距探测器距离为r的体单元产生的伽马通量密度可表示为[14]

(1)

式(1)中：J为探测器处的伽马通量密度，单位为伽马光子数/(s·cm2)；a为放射性物质伽马射线的放射性强度，单位为伽马光子数/(g ·s)；q为岩石中放射性物质含量，单位为g/g；ρ为地层密度，单位为 g/cm3；μ为地层对伽马射线的吸收系数，单位为1/cm。利用式(1)对半径为r0的半球体进行积分，得到半径为r0、锥角为θ0的均匀锥形区域对探测器产生的伽马通量为:

(2)

对于图3中左图所示的相交情况，将锥形体分成A、B、C三部分，各部分的伽马通量可通过下面积分得到:

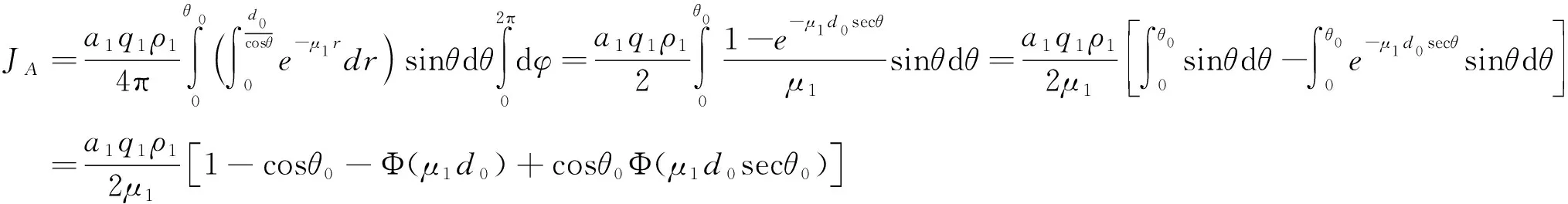
(3)

(4)

则方位1处的总伽马通量表达式为J1=JA+JB+C。上述公式中，d0为探测器到边界的距离，r0为仪器的探测半径，θ0为锥形体的锥角，在公式推导中用到了金格函数Φ(x)[15]

(5)

对于图3中右图所示的相交情况，将锥形体分成D、E、F三部分，各部分的伽马通量可通过下面积分得到

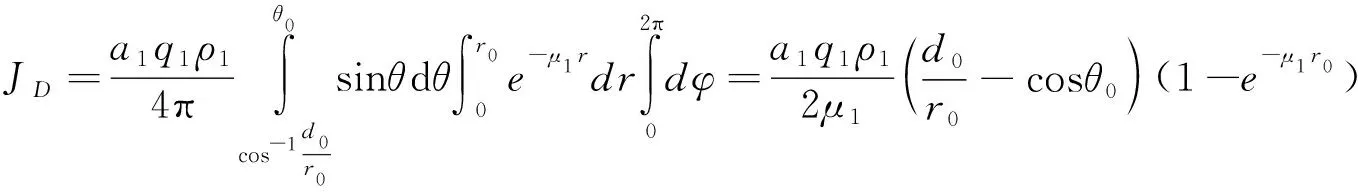
(6)

(7)

(8)

则方位1处的总伽马通量表达式为

J1=JD+JE+JF

利用上面伽马通量表达式，考虑不同地层与锥形体相交情况，图2所示4个方位的伽马探测器响应表达式可写成如下形式：

1)只与上围岩界面相交

(9)

2)只与下围岩界面相交

(10)

3)与上下围岩界面均相交

(11)

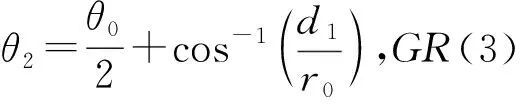
得到GR(1)～GR(4)后，选择正弦函数作为拟合函数，对GR(1)～GR(2)之间和GR(3)～GR(4)之间的方位进行插值，进而得到0°到180°之间方位的伽马值。各方位处的伽马响应值拟合公式为：

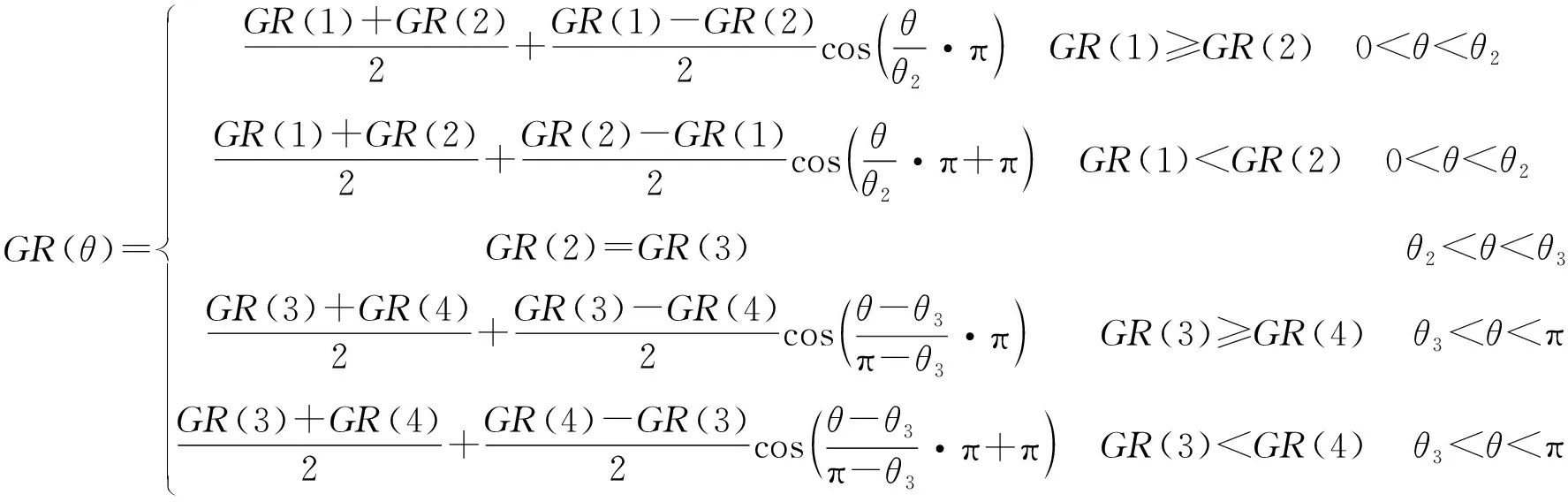
(12)

2 数值模拟

2.1 参数的工程简化

2.2 数值模拟

参考文献[17]中通过蒙特卡罗方法模拟得出的伽马探测半径在0.15～0.2 m的结论，本文模拟中选定伽马探测半径为0.2 m，锥形体的锥角大小则参考文献[13]，选定为90°。

首先考察仪器钻进轨迹朝一个方向穿过目的层时的情况，设定目的层厚为0.4 m，上下围岩放射性参数为100 API，中间目的层放射性参数为20 API，轨迹从上向下接近于水平穿过目的层的模型及成像结果如图4所示。

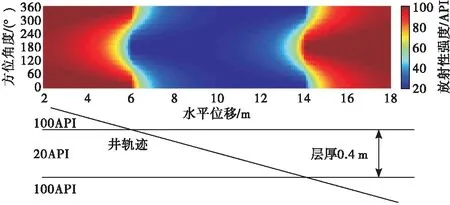
图4 仪器从上向下穿过地层成像图

图4下方为模型，上方为按水平位移展示的成像图。从成像结果可以看出，随着轨迹从上向下穿过地层，顺着图像出现的顺序观察，将0°方位附近区域比作人的嘴角位置，则地层界面附近图像呈现出嘴角向下，类似于哭脸的形态，且该形态与界面两侧地层放射性高低无关，只与穿过界面的方向有关，但通过观察该图像颜色沿井轨迹的变化趋势，如颜色是从红色变化到蓝色，还是从蓝色变化到红色，可以判断出穿过的界面两侧的地层放射性高低。

保持地层模型参数不变，将图4中井轨迹改为从下向上反向穿过地层，成像图的形态应该与图4刚好呈水平左右镜像形态(这里不再重复展示)，则轨迹穿过界面时图像应该呈嘴角上扬，即类似于笑脸的形态。由此可见，根据轨迹穿过界面时图像呈现出笑脸还是哭脸形态，以及颜色的变化趋势，可以判断出仪器是从上向下还是从下向上穿过界面，以及界面两侧的地层放射性高低。

将层厚增大到2 m，其余地层模型参数不变，考察轨迹从上围岩进入目的层后，分别沿靠近目的层上边界和下边界水平钻进一段距离后，再返回上围岩的情况，模型及成像图如图5和图6所示。

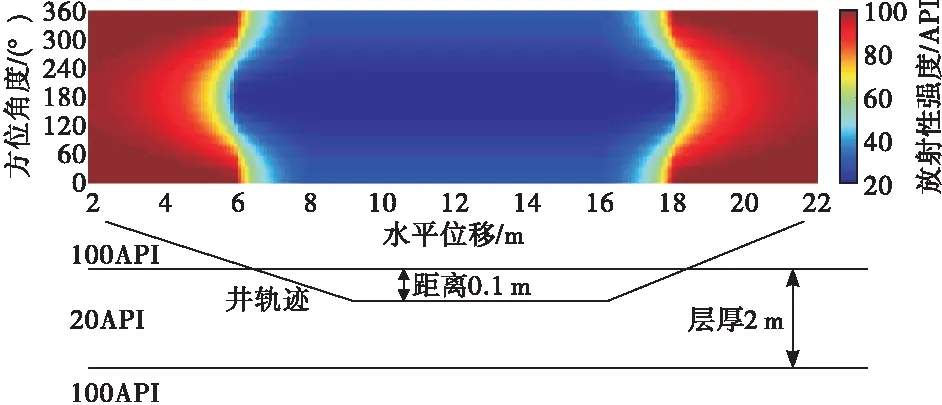
图5 轨迹从上围岩进入目的层后靠近上界面穿行再返回上围岩成像图

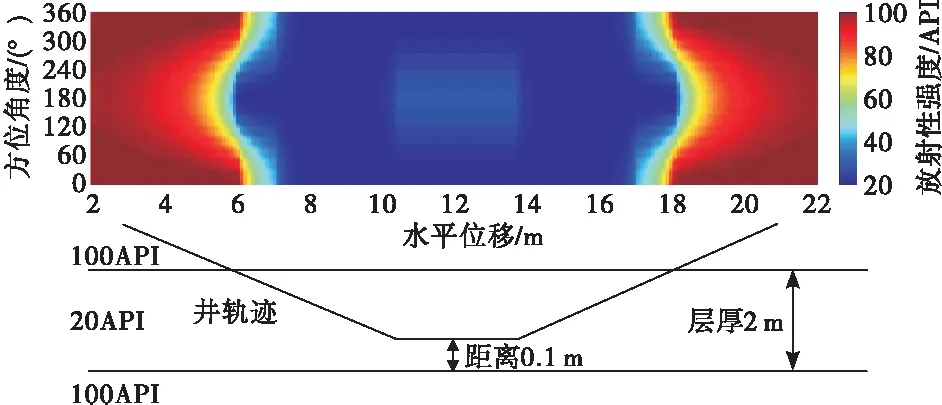
图6 轨迹从上围岩进入目的层后靠近下界面穿行再返回上围岩成像图

观察图5，当轨迹向下进入目的层时，在界面处呈现出哭脸的形态，随后靠近上界面穿行，此时方位0°附近的响应受上围岩和目的层的共同影响，因此响应值介于两者之间，由于探测深度所限，方位180°附近的响应仅受目的层单一影响，因此响应值等于目的层实际值，当轨迹穿过上界面再回到上围岩时，界面处呈现出笑脸形态。整幅图像看起来就像是一只闭着的眼睛。

对比观察图6，两者的不同在于轨迹进入目的层后靠近下界面穿行。由于目的层厚度远大于仪器探测深度，则在轨迹位置处于目的层中部区域时，所有方位的响应值均只受目的层单一影响，当靠近下边界后水平钻进时，方位0°和方位180°附近的响应值与图5中靠近上界面穿行时的恰好相反，颜色对调，其余部分的图像均与图5相同，这样在目的层内呈现出与目的层实际值对应的颜色区域将方位180°附近的响应值对应的颜色区域包裹起来的形态，整幅图像看起来就像是一只睁着的眼睛。

保持地层模型参数不变，考察仪器从下围岩进入目的层后，分别沿靠近目的层上边界和下边界水平钻进一段距离后，再返回下围岩的情况，模型及成像图如图7和图8所示。

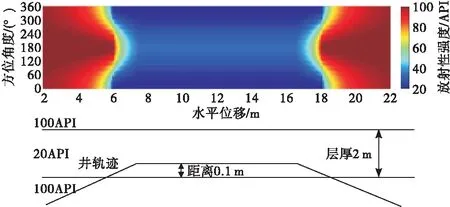
图7 轨迹从下围岩进入目的层后靠近下界面穿行再返回下围岩成像图

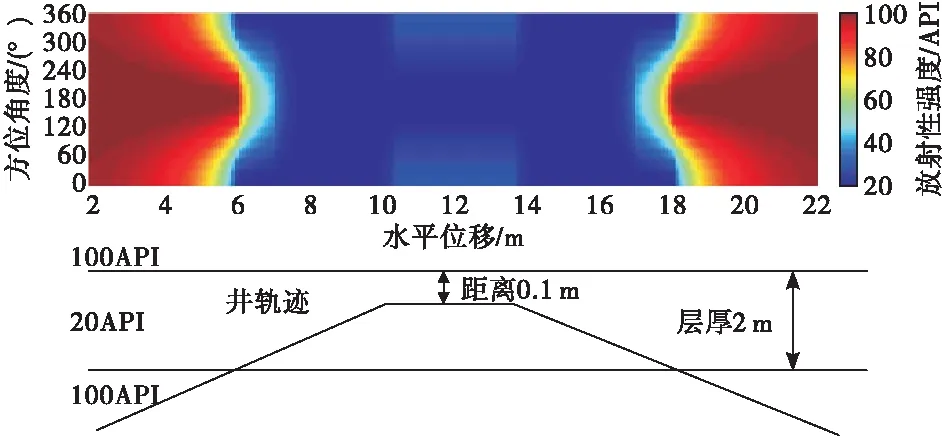
图8 轨迹从下围岩进入目的层后靠近上界面穿行再返回下围岩成像图

观察图7，当轨迹向上进入目的层时，在层界面处呈现出笑脸的形态，随后靠近下界面穿行，方位0°附近的响应等于目的层实际值，方位180°附近的响应受下围岩和目的层共同影响，则在目的层内呈现出与目的层实际值对应的颜色区域将方位180°附近响应值对应的颜色区域夹在中间的形态，轨迹向下返回下围岩时，层界面处呈现出哭脸的形态。

对比观察图8，在层界面处图像的形态与图7相同，在目的层内图像的形态为图5和图6的结合，呈现出与目的层实际值对应的颜色区域将方位0°附近响应值对应的颜色区域一分为二的形态。

3 结 论

本文在自然伽马测量理论的基础上，根据伽马成像测量的原理特点，建立了伽马成像正演模型。该模型确定了4个关键方位，每个方位处的伽马响应均通过对锥形体进行积分得到。利用得到的4个方位处的伽马响应值，选择正弦函数作为插值函数，对其余方位处的伽马值进行插值，最终得到所有方位处的伽马值。该方法只需对解析公式进行编程计算，具有实时性的优点，方便与地质导向作业相结合。利用本算法对地质导向作业中常见的几种正演模型进行了模拟，通过对模拟结果的分析，发现如下规律：

1)顺着图像出现的顺序观察，当井轨迹从上向下穿过层界面时，在界面附近呈现出类似哭脸的形态；轨迹从下向上穿过界面时，则呈现出笑脸的形态，且该形态与界面两侧的地层放射性高低无关，但通过观察颜色的变化趋势，可以判断界面两侧地层的放射性高低。

2)在轨迹穿过上界面向下钻进目的层后，再从目的层向上穿出上界面情况下，当目的层中轨迹靠近上界面穿行且仪器探测不到下界面时，整幅图像看起来就像是一只闭着的眼睛；当目的层中轨迹靠近下界面穿行且仪器探测不到上界面时，整幅图像看起来就像是一只睁着的眼睛。

3)在轨迹穿过下界面向上钻进目的层后，再从目的层向下穿出下界面情况下，当目的层中轨迹靠近下界面穿行且仪器探测不到上界面时，在目的层内呈现出与目的层实际值对应的颜色区域将方位180°附近响应值对应的颜色区域夹在中间的形态；当目的层中轨迹靠近上界面穿行且仪器探测不到下界面时，在目的层内呈现出与目的层实际值对应的颜色区域将方位0°附近响应值对应的颜色区域一分为二的形态。

这些规律的发现，使我们对伽马成像的响应特点有了更深入的理解和认识，为实现更好的地质导向应用奠定了基础。