基于非结构化有限元的三维井地电阻率法约束反演
2023-01-03王智王程方思南
王智,王程,方思南
(1.长江大学 电子信息学院,湖北 荆州 434023;2.中煤科工集团 西安研究院有限公司,陕西 西安 710077;3.长江大学 地球物理与石油资源学院,湖北 武汉 430100)
0 引言
电磁法勘探是以地壳中不同岩石之间的电性差异为物理基础(如导电性、导磁性、介电性以及电化学性质的差异),通过观测研究人工或天然形成电磁场的时间和空间分布规律,从而达到寻找地下有用矿产资源、查明地下地质构造以及解决地质问题的目的[1]。电磁法勘探方法主要分为基于几何测深原理的直流电法、基于频率域测深原理的大地电磁法(MT/AMT/CSAMT)与基于时间域测深原理的瞬变电磁法(TEM)[2]等。直流电阻率法是电法勘探的最经典方法之一,在金属矿产、非金属矿产、煤田、油气及地下水等资源勘探中获得广泛而有效的应用,并已拓展到水文、工程、环境、考古等与国民经济建设、人类社会生活密切相关的探测领域[3]。直流电阻率法有多种灵活的观测方式,如单极、偶极及多极装置的电剖面法、电测深法等,井地电阻率法是在井中供电,在地面接收电磁场的一类电法,供电装置总是放入钻孔深部使其接近于被探测的对象,从而增大电流强度或被接收的异常响应[4-5],井地电阻率法主要用于金属矿矿山的二次资源勘查及油藏边界的预测[6]等,通常采集装置沿着具有不同电极阵列的平行线在网格上进行数据采集,并使用3D反演算法进行解释。随着计算机及数值计算技术的发展,电阻率三维正反演算法分别在网格的剖分(结构化[7-12]、非结构化[13-21]),数值方法(有限差分法[22-27]、有限元法[28-29]),目标函数的求解(高斯—牛顿法(GN)[3, 19, 30-37]、拟牛顿法(QN)[38-54]、非线性共轭梯度法(NLCG)[45, 51, 55-63]等)等方面取得很大进展。
由于结构化单元的网格不能适应复杂地形下的电阻率三维反演,因此非结构有限元方法在复杂地形电阻率三维数值模拟中取得极大成功,非结构化网格具有单元质量可控、允许局部加密、能够模拟复杂几何模型等优点,使得三维非结构有限单元求解效率大幅提高。同等计算精度情况下,非结构化网格相对于结构化规则网格,计算时间和存储量均可下降约一个数量级[3]。在电阻率三维反演中,由于反演参数多且数据量大,雅可比矩阵(偏导数矩阵)对巨大的计算量和存储需求难于克服,许多学者研究可避开计算雅可比矩阵的反演算法,Zhang等[26]、吴小平等[36]引入共轭梯度方法,解决了电阻率三维正演效率及三维反演中雅可比矩阵求取、存储两方面问题,实现比较快速有效地电阻率三维反演。在三维数据反演中采用的最优化方法主要有非线性共轭梯度法(NLCG)、高斯—牛顿法(GN)和拟牛顿法(QN)。NLCG和QN只需要目标函数的梯度信息,无需显式计算灵敏度矩阵,由于仅仅使用了目标函数的一阶导数(梯度)信息,只有线性收敛性,模型需要反复更新很多次才能收敛到理想的值,而GN法同时使用了目标函数的一阶导数(Gradient)和二阶导数(Hessian)的信息,表现出近似二次收敛性,所需的模型更新次数远远少于NLCG和QN法,每次高斯牛顿迭代的法方程使用预条件共轭梯度法(PCG)求解,不仅可以避免显示求解和存储灵敏度矩阵,还能减少PCG的迭代次数来减小反演的计算时间。由于反演的非线性特征,这种非精确求解对于线性化迭代反演不仅减小了计算量,而且还避免了每次GN迭代中对法方程的过度求解,因此在反演搜索过程中有机会跳出局部极小值[33]。
压制电阻率三维反演多解性的有效方法是发展约束反演,将已有的先验信息通过数学手段加入到反演过程中,提高反演精度。Sasaki Y[21]提出了光滑约束,使得相邻网格之间的电阻率差异极小,光滑过渡,这种约束具有天然的合理性,已经成为电阻率反演中常用的一种约束形式;Kim等[64]按照光滑约束的施加形式,定义了一个新的参数向量来表征模型参数,将不等式约束施加到反演方程中,获得了不错的效果;Li等[65]利用约束最优化里的内点罚函数法将不等式约束条件加入到目标函数里,提高了反演成像的精度;黄俊革等[66]和宛新林等[67]分别对粗糙度矩阵进行改进,提高了三维反演的效果;刘斌等[68]在反演目标函数中引入自适应加权光滑约束,控制深部分辨率并在其文献中[69-70]讨论了不等式和先验结构约束条件的加入方法,去除了反演成像中的假异常和多余构造,明显地压制了电阻率探测反演的多解性问题。
电磁探测反演是典型的不适定问题,易造成反演结果的多解性,不适定性是反演自身固有的特征,没有求解的附加信息这一本质困难是很难克服的[71],如何利用相关技术引入先验信息实现地下结构的高精度成像是未来电磁法重要的发展方向之一[72]。电阻率的变化范围是一个很重要的先验信息,如何将不等式约束施加到反演方程中是一个关键性的难题。Kim等[64]采取的方法是一种经验式施加方式,在反演过程中该约束项繁琐、不容易理解;Li等[65]采用内点罚函数法,在目标函数中加入对数形式的障碍函数,这种施加形式简单,但是内点法要求初始值的选取必须在可行域内,并且初始点应选择一个离约束边界较远的可行点,太靠近某一约束边界会造成求解的困难。如果约束条件较为复杂时,选择初始点有一定难度,并且内点法只能解决约束为不等式情形,外点法可以解决约束为等式和不等式混合的情形,外点法对初始点也没有要求。结合前人研究与上述反演存在的问题,本文将表征模型参数变化范围的不等式约束作为先验信息以外点罚函数的方式引入到目标函数中[73],选择井地观测方式、非结构化四面体的有限单元法与高斯牛顿法(GN)相结合方式实现了井地电阻率法的三维约束反演算法,通过典型三维理论模型合成观测数据来验证所开发的算法的稳定性及有效性。
1 三维正演理论
1.1 控制方程
三维直流电阻率法点电流源场总电位满足的偏微分方程及其边界条件为[9, 16, 74]:
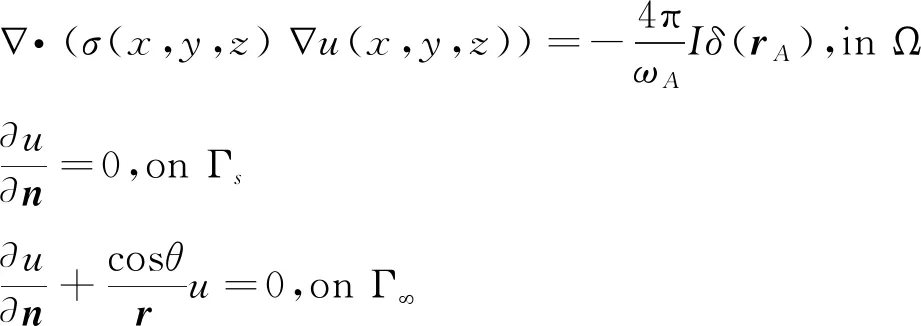
(1)
其中:σ是岩石电导率;u是电位;I是电流强度;δ是狄拉克函数;rA是源点位置;ω是源点对地下区域Ω的张开角,若源点在地面,则ωA=2π;若源点在地下,ωA=4π,n是边界Γ∞边界上的外法向向量;r是点电源到边界点的距离;Γs是自然边界条件;Γ∞是无穷远边界;θ是无穷远边界上点的外法向向量n与场源到边界点距离r之间的夹角。采用加权余量法可导出式(1)对应的变分问题的积分方程:
(2)
计算区域采用四面体剖分与线性差值,最终形成的大型稀疏对称线性方程组,矩阵表达形式如下:
Ku=P
,
(3)
其中:K是一个n×n的对称矩阵;u为n×1列向量,表示三维网格节点上的电位向量;P是含有场源信息的列向量;P=(0,…,I,…,0),为了节约内存采用行压缩存储(compressed sparse row or compressed row storage)处理系数矩阵K,使用对称超松弛预条件共轭梯度算法[11, 20](SSORPCG)求解方程组(3)。
1.2 算法验证
为了验证本文正演程序的正确性,本文设计了一个均匀半空间中埋藏球体的模型,如图1a所示,该模型为均匀半空间中嵌入一个球形异常体[16],球体的半径为R=2.25 m,球体中心坐标为(0,0,-4.5),球体电阻率值ρ0=1 Ω·m,地层围岩电阻率值为ρ1=10 Ω·m,点电流源A坐标在(-5,0,0)处,电流大小为1 A,测量电极M沿x方向,间距为0.25 m。整个计算区域大小为500 m×500 m×300 m,目标区域大小为100 m×100 m×100 m,网格节点总数为273 582,网格单元总数为1 625 838,网格剖分效果见图1b~1d,分别在源点、测点与球体处进行了加密处理。采用pole-pole装置,由本文的有限元正演程序计算得到测点处电位值,并与解析解进行了比较,如图2所示,本文的计算结果与解析解有很好的一致性,最大误差小于0.34%(见图3)。
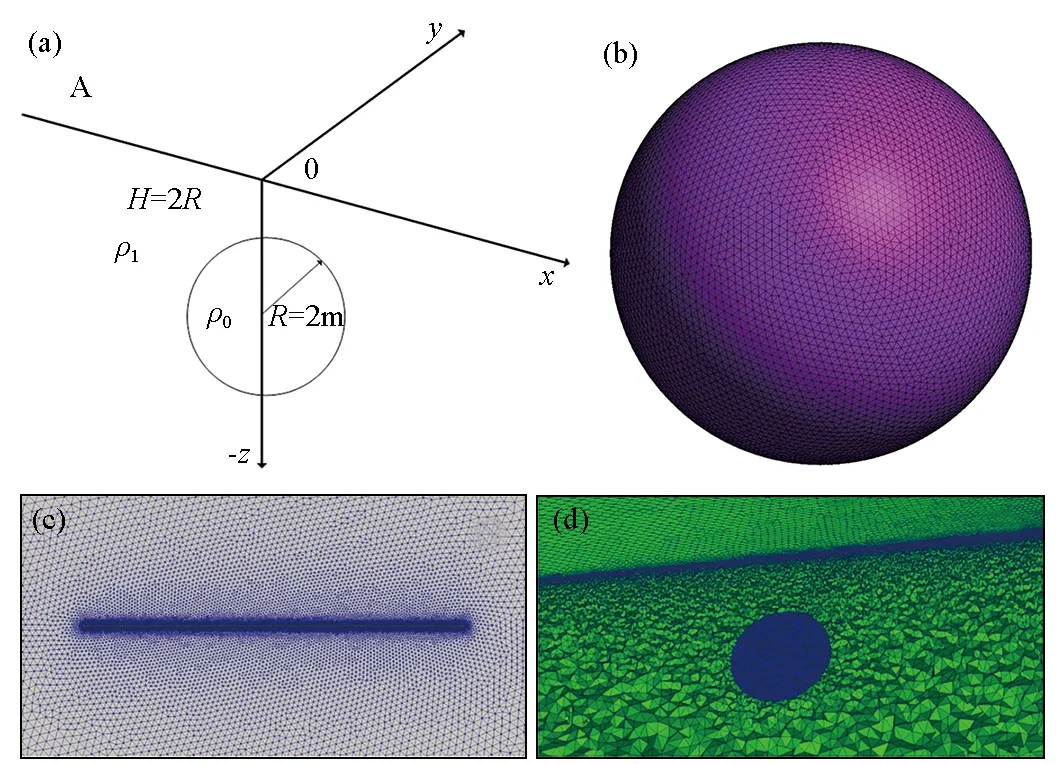
a—球体模型示意;b—球体模型网格剖分放大效果;c—点与测点网格加密效果;d—网格剖分示意
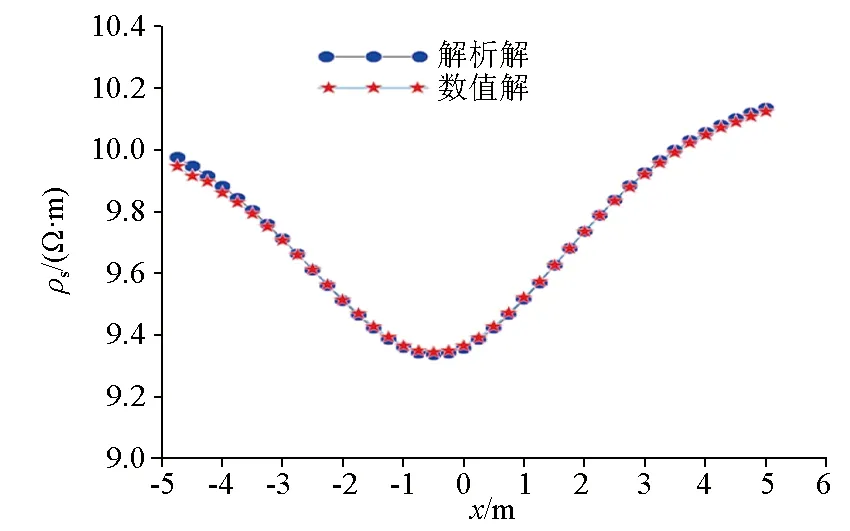
图2 地下球体的解析解与数值解对比
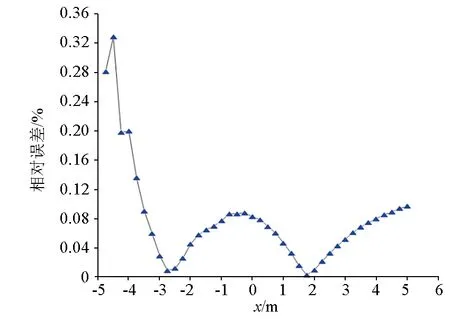
图3 解析解与数值解的相对误差
2 三维反演理论
2.1 目标函数
依据Tikhonov正则化理论,最小二乘意义下的反演目标函数为[3, 19, 31]:
Φ(m)=Φd(m)+λΦm(m)=
(4)
其中:F(m)为正演响应函数;m为模型参数(mi,i=1,2,…,M),dobs(dj,j=1,2,…,N)为观测数据,Wd为N×N阶观测数据误差加权矩阵,Wd=diag(1/σ1,1/σ2,…,1/σn),σi为第i个观测数据的标准差;Wm为M×M阶模型加权矩阵,通常用模型单元的离散差分算子来定义,一般取一阶正则化约束。λ为正则化因子,用来平衡数据拟合和模型光滑度的权重;mref为含有模型参数先验信息的参考模型。反演的观测参数dobs为pole-pole的电位值,模型参数为单元的电导率值σ,由于变化范围很大,为了反演的稳定性,通常采用对数来标定观测数据及模型参数,即d=lnφobs,m=lnσ。光滑约束的施加请参考文献[62],不等式约束施加的原理详见文献[62-63],常规电阻率反演目标函数中构造出带有不等式约束的反演目标函数见式(5):
,
(5)
式中:mmin,mmax为每个单元网格电阻率的上下限。式(5)即为本文带不等式约束条件的三维电阻率反演的目标函数,与常规三维电阻率反演目标函数相比,该方法增加了不等式约束项,该表达式简单、容易理解、易于实现。目前常用于三维电阻率反演的最优化方法有拟牛顿法(QN),高斯牛顿法(GN)、非线性共轭梯度法(NLCG)以及这些方法的变种[33,75]。对目标函数(5)进行二阶Taylor展开,忽略高阶项得到高斯—牛顿法(Gauss-Newton,GN)的法方程(normal equation)为:
H(m)△(m)=-g(m)
,
(6)
其中:g(m)为目标函数的一阶导数(梯度矩阵,Gradient),H(m)为目标函数的二阶近似导数(海森矩阵,Hessian),分别表示如下:

,
(7)
其中:J(m)为灵敏度矩阵(正演响应函数F(m)的一阶导数),Wc为不等式约束矩阵:其元素Wc(i,j)取值如下:
(8)

2.2 模型更新
利用CG法求得法方程(6)的解Δm后,需要进行线性搜索来获得每次GN迭代的模型更新量,更新公式为:
mk+1=mk+αΔm
,
(9)
其中:α为模型的更新步长,步长α的精确线搜索往往需要大量的计算,一般采用非精确一维线性搜索方法得到步长,常用的策略是采用Wofe-Powell准则来进行非精确线性搜索得到更新步长α,Wofe-Powell准则包括充分下降条件与曲率条件,公式为:
(10)
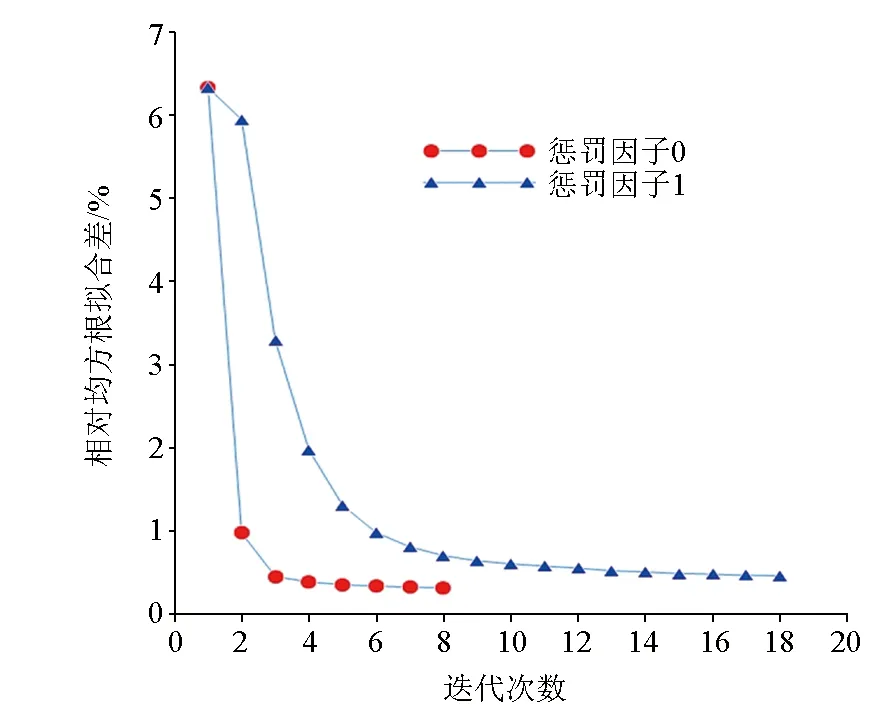
其中:Φ为正演算子,mk为第k次反演迭代的模型参数;αk为迭代步长;pk为搜索方向;c1与c2为常数,满足0 GN-CG法反演流程如下[73, 76]: GN-CG反演算法1) 给定初始模型m0与参考模型mref,设置收敛系数ε,正则化因子λ和惩罚因子μ,给定光滑度矩阵Wm;2) 开始GN-CG 迭代, 设k=1,2,…,NmaxGN;3) 计算Δdk=dobs-F(mk),并计算r0=-gk;gk=-JTkWTdWdΔdk+λWTmWm(m-mref)+μ[min(m-mmin,0)-min(mmax-m,0)];4) 开始CG 迭代, 令Δm=0,p0=r0,设i=1,2,…,Nmaxcg; 4-1)计算Hk=JTkWTdWdJk+λWTmWm+μWc, 得到Hkpi; 4-2)计算ti=rTiripTiHpi; 4-3)计算Δmi+1=Δmi+tipi; 4-4)计算ri+1=ri-tiHkpi; 4-5)计算βFRi=rTi+1ri+1rTiri; 4-6)计算pi+1=ri+1+βipi;5) CG迭代结束, 求得Δm,根据Wofe-Powell条件(式12)进行一维搜索得到最优步长αk,更新模型:mk+1=mk+αkΔmk;6) 如果RMS<ε 则停止GN-CG迭代,输出mk,否则令k=k+1 转到步骤3); 为了验证开发的基于不等式约束井地电阻率三维反演算法的正确性与有效性,本文设计了2个三维模型来分别模拟井地电阻率法的测量情况,并对这2个三维模型的合成数据进行三维反演测试。本文的所有计算均在小型计算机上完成,其配置CPU为Intel I7-4712MQ,主频为2.3 GHz,内存16 G,正反演程序均采用Inter Fortran编译运行,非结构化四面体网格剖分采用Gmsh-4.8.4[77],非结构化四面体网格的显示采用Paraview-5.6.0[78]。 长方体模型如图4a、4b所示,围岩电阻率ρ0=100 Ω·m,低阻体电阻率ρ1=10 Ω·m,低阻长方体大小为10 m×10 m×5 m,顶面埋深h=5 m,底面埋深为10 m。蓝色三角形代表钻井井口位置(18,25,0)与(32,25,0),异常体离两边钻井的水平距离d=2 m。本次反演采用的测线范围为10~40 m,测线之间的间距为2 m,每条测线上16个测点,测点M(测量电极)沿x方向的位置坐标为x=10~40 m,y=10~40 m,间距为2 m;源点A(供电电极)移动范围在井下-4~-20 m,间隔为4 m,一共设置10个点源;地表测量装置位置见图4c。为了测试反演算法的稳定性,避免反演偏差,反演网格采用不同于合成数据所用的正演网格:正演网格分别在测点、源点与异常体附近进行网格加密;反演网格在源点与测点处进行加密,不仅提高了正演的精度,还减少了源点附近的数值模拟误差,测点局部加密示意图见图4d。图4e、图4f分别为正演与反演所使用的非结构化四面体网格,正演网格单元总数为1 288 357。反演网格中网格单元总数为1 090 207,通过三维有限元正演程序共得到2 560个一次场的”电位实测数据”,正演一次约130 s,反演一次约14 400 s。反演参数选择如下:正则化参数λ=0.05,惩罚因子μ=1.0,在反演过程中始终保持不变,反演终止的收敛系数ε=1.0×10-5,反演的迭代次数10次,反演过程中RMS变化如图5所示。从图6可以看出,数据拟合差稳定下降,说明本文的带约束的GN法对于三维井地电阻率法的数据收敛性较好,图5分别给出了传统正则化反演与施加不等式约束反演结果的xoy与xoz剖面,两种反演方法得到的模型与真实模型吻合较好,地下低阻异常体的位置与电阻率值基本一致,验证了本文反演方法的有效性。 a—xoy水平截面; b—xoz垂直断面;c—三维异常体模型;d—测点加密示意;e—正演网格;f——反演网格 图5 迭代次数与RMS的关系 a—传统电阻率反演结果z=-7 m处xoy切片;b—传统电阻率反演结果y=25 m处xoz切片;c—施加不等式约束的反演结果z=-7 m处xoy切片;d—施加不等式约束的反演结果y=25 m处xoz切片;e—传统电阻率反演结果的三维剖面(电阻率小于50 Ω·m);f—施加不等式约束反演结果的三维剖面(电阻率小于50 Ω·m) 为了测试所开发的反演算法对于复杂模型的有效性,考虑浅地表存在的电阻率异常干扰,在背景为1 000 Ω·m的均匀半空间中放置5个电阻率异常体[79-80],其中3个长方体顶界面位于浅地表以下10 m(S1,S2,S3),用于模拟浅地表的电阻率异常干扰,另外两个顶界面埋深分别为60 m和95 m的长方体(B1,B2)模拟探测目标体,各项参数见表1,三维模型见图7a。整个模型的研究区域(目标区域与边界区域)x、y、z这3个方向的剖分范围分别是(-1 000,2 000)、(-1 000,2 000)和(-1 500,0),目标区域x、y、z这3个方向的剖分范围分别是(0,1 000)、(0,1 000)和(-500,0)。采用的测线范围为50~950 m,测线之间的间距为50 m,每条测线上19个测点,测点M(测量电极)沿x方向的位置坐标为x=50~950 m,y=50~950 m,间距为50 m;井口坐标分别为(500,200,0)与(500,800,0),源点A(供电电极)移动范围在井下-40~-360 m,间隔为80 m,一共设置10个点源。地表测量装置与点源位置分别见图7b与7c。正演网格单元总数为2 511 215,反演网格中网格单元总数为1 037 303,通过三维有限元正演程序共得到3 610个一次场的”电位实测数据”,正演一次约275 s,反演一次约17 039 s。 a—三维异常体模型位置; b—地表数据观测系统;c—垂直剖面yoz; d—非结构化网格加密示意 表1 长方体参数 浅层地震勘探、地质雷达探测法对异常体界面识别和定位方面具有较好的效果,在电阻率探测时利用这些方法获得的异常体位置与形态信息是一种极为重要的先验构造信息[62, 63, 69],因此在三维井地电阻率反演中将构造位置的先验信息作为局部约束加入。由其他地球物理探测方法假设可知异常体的构造位置与形态信息,由探区矿石标本物性参数可得:分别在①250 m≤x≤350 m,250 m≤y≤350 m,-50 m≤z≤-10m处异常体的电阻率值在220 Ω·m以内,将此处网格单元的电阻率上限设为220 Ω·m,下限设为0;②300 m≤x≤700 m、400 m≤y≤500 m、-50 m≤z≤-10 m处异常体的电阻率值在120 Ω·m以内,将此处网格单元的电阻率上限设为120 Ω·m,下限设为0 Ω·m;③350 m≤x≤700 m、650 m≤y≤700 m、-50 m≤z≤-10 m处异常体的电阻率值在2 200 Ω·m以内,将此处网格单元的电阻率上限设为2 200 Ω·m,下限设为1 800 Ω·m;④300 m≤x≤650 m、300 m≤y≤400 m、-260 m≤z≤-60 m处异常体的电阻率值在2 200 Ω·m以内,将此处网格单元的电阻率上限设为2 200 Ω·m,下限设为1 800 Ω·m;⑤400 m≤x≤500 m、500 m≤y≤650 m、-275 m≤z≤-95 m处异常体的电阻率值在120 Ω·m以内,下限设为0 Ω·m。各项反演参数的设置与模型1的反演参数设置一样。图8c与图8d为施加不等式约束后的电阻率反演结果,由反演结果可以看出,5个异常体水平和横向的分辨率较传统反演结果(图8a,图8b)有了明显提高,与原模型在电阻率值、规模、位置、形状等特征方面均基本一致,带不等式约束的正则化反演能够得到更为精确的三维反演成像结果。 a—传统正则化反演x=400 m处yoz剖面; b—传统正则化反演x=600 m处yoz剖面;c—约束反演x=400 m处yoz剖面; d—约束反演x=600 m处yoz剖面 本文实现了一种以外点惩罚函数法的方式将带有电阻率取值范围的不等式约束施加到井地电阻率三维反演方程中的GN-CG反演算法,正演采用有限元法与非结构化网格对控制方程离散化并使用SSORPCG法求解离散所得的大型线性方程;反演中采用高斯牛顿最优化算法,在目标函数中加入不等式与构造约束来降低反演的多解性。以上这些技术的综合使用,使得本文带约束的GN-CG算法稳定且准确,适用于陆地与井中的电阻率法勘探情况。通过对理论模型的反演试算,验证了本文反演算法的可靠性与有效性,带约束的三维井地电阻率反演方法能得到更精确的反演结果;惩罚因子的取值与不等式约束的范围给定是两个难点,本文惩罚因子的取值采用的是实验法,过大或者过小的惩罚因子都会影响反演的效果,有时甚至会出现不收敛的情况,可以通过结合其他物探方法给出异常体较为准确的边界范围以及电阻率值的上下限,给出的范围越精确,反演结果就越准确。2.5 反演流程

3 合成数据反演
3.1 平坦地形下单个异常体
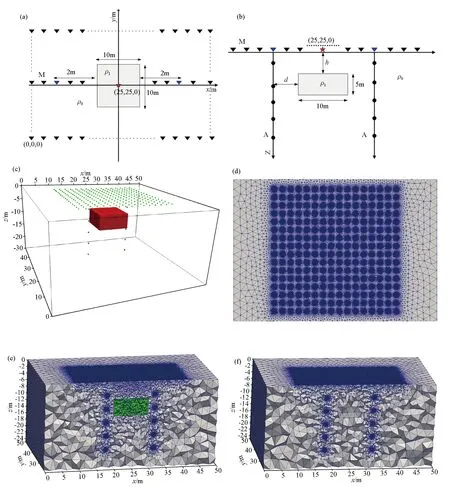

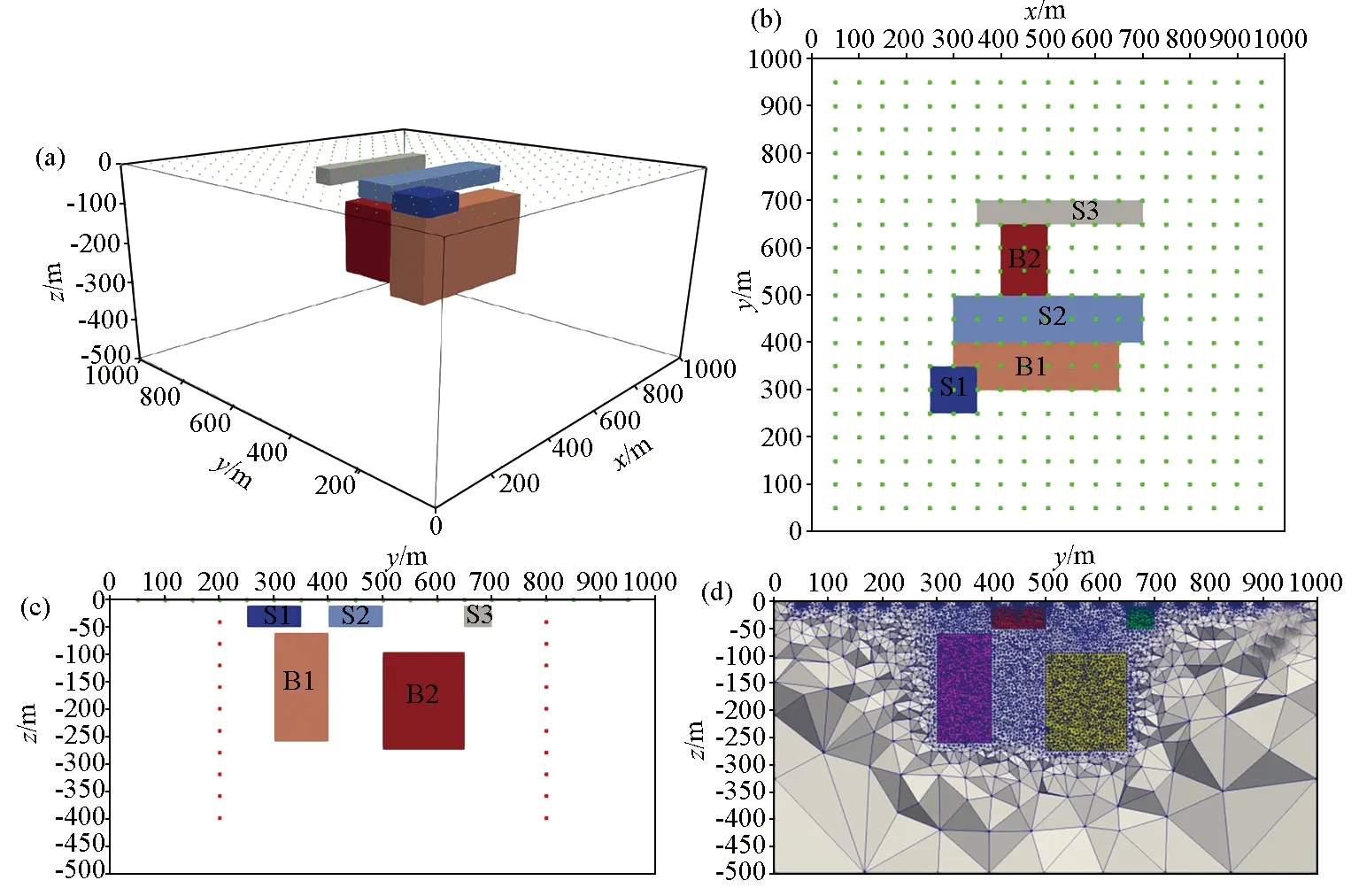
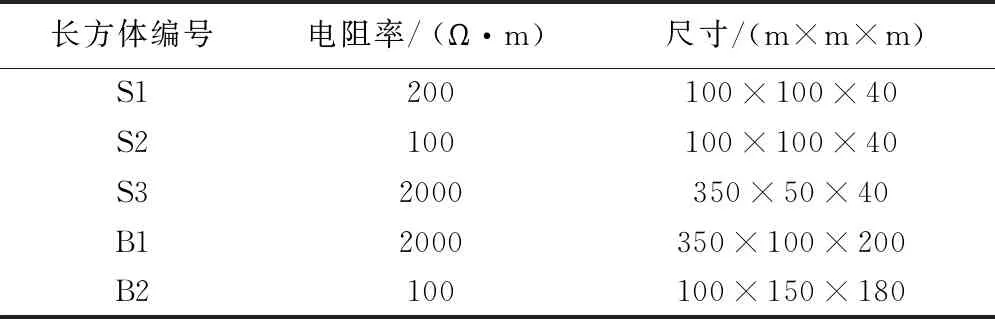
3.2 五个异常体模型

4 结论
