基于三方博弈建筑绿色供应链演化路径与仿真分析

周俊 徐新卫 谢尚金 邓佳佳

(1.广东科技学院管理学院，广东 东莞 523000；2.安徽工业大学管理科学与工程学院，安徽 马鞍山 243000；3.中建东方装饰有限公司，上海 200122)

引言

习近平总书记在2020年联合国大会发表的一般性辩论重要讲话,提出中国的碳中和目标“二氧化碳排放力争于2030年前达到峰值,努力争取2060年前实现碳中和”,表明我国对全球疫情后实现绿色复苏和低碳转型做出积极贡献[1]。然而,作为国民经济支柱产业之一的建筑业,依旧表现为高消耗、高污染的发展模式。2018年全国建筑全过程能耗总量占全国能源消费总量比重为46.5%；全国建筑全过程碳排放总量占全国碳排放的比重为51.3%[2],资源过度利用、环境污染等问题越来越制约建筑业的可持续发展。因此,为了调整和优化建筑产业生产方式,企业必须转变建筑生产的管理模式,借鉴制造业先进的供应链管理思想,结合可持续发展的理念,实施建筑绿色供应链管理模式。建筑绿色供应链是在建筑的全生命周期内,在节约资源、减少环境污染的条件下为人们提供环保舒适、与自然融合的绿色建筑产品。通过物流、信息流、资金流在绿色建材供应商、建设单位、施工单位、设计单位、消费者、回收再处理企业等的流动,形成一个闭环的网链结构模式。与其他传统供应链不同,除了追求效益最大化、顾客满意等目标外,其更强调将环境意识贯穿于整个供应链中[3],注重产品生命周期内的绿色运作和管理,以经济社会效益和环境综合利用效益为最优目标。结合绿色供应链管理的基本原理[4],建筑绿色供应链的框架模型如图1所示。

图1 建筑绿色供应链框架模型

目前演化博弈理论已在建筑领域广泛应用。Shi等[5]建立演化博弈模型来研究建筑供应商之间的合作趋势,结果表明,供应商的生产能力、业主与供应商的合同、业主的激励机制直接影响供应商的合作倾向。Feng等[6]则在假设惩罚和激励条件,建立预制件生产商之间的演化博弈模型,得出了在合作和非合作2种情况下都存在稳定的演化策略,且演化结果受2种决策过程初始比例的影响。政府可以通过有效的惩罚和激励机制,支持生产企业建立牢固的合作伙伴关系,降低预制构件供应链的初始成本,实现双赢。黄定轩[7]基于收益-风险的角度,建立了绿色建筑项目中开发商与客户在有限理性下需求侧演化博弈模型。梁喜[8]从绿色建筑供给侧角度出发,构建政府动态奖惩政策下动态补贴与静态税收、静态补贴与动态税收、动态补贴与动态税收3种情形下的演化博弈模型,得出动态补贴与静态税收为推动绿色建筑发展的帕累托最优解。王荆[9]系统地分析了绿色建筑发展中的利益相关者和影响因素,构建政府部门、房地产开发企业和消费者的两两演化博弈模型并进行参数分析。冯辉红[10]认为,绿色采购在很大程度上能减少房地产行业的能源消耗,从收益、风险与损失的角度分析了建材生产商和房地产开发商供需双方的演化博弈模型以及不同情况下行为决策选择。通过对以上研究结果的梳理可知,目前运用演化博弈理论研究大多集中在政府、开发商和消费者两两之间的关系,对于利益相关者回收企业的研究较少,但回收企业是建筑绿色供应链能够闭环,发挥价值的关键环节。基于此,本研究从绿色供应链微观层面,构建建筑绿色供应链生态系统的生产种群、消费种群和分解种群的三方演化博弈模型,将三者的决策行为和演化过程中重要因素的相互关系更真实的呈现出来,为建筑绿色供应链的实施提供建议和参考支持。

1 基本假设和模型构建

在建筑绿色供应链生态系统中,对运行环境影响较大的利益相关者主要包括生产建筑产品的生产种群、一定数量的消费种群和分解种群。其中,生产种群以建设企业为核心,虽然不直接参与工程项目的建造过程,但是建设单位对建筑及其生产的绿色性要求决定承包商的施工行为和消费者的消费行为。面对建筑的开发问题上,房地产开发企业的策略集Sx＝{开发,不开发}。为了自身长远发展、政府的政策措施、市场的供需等,建设单位会参与建筑绿色供应链的合作,投入相应的资源提升建筑的节能环保水平并采取措施激发消费者购买量；也可能由于初期造价成本过高、市场不确定性因素而不与建筑绿色供应链的合作,维持现有的技术水平开发传统建筑。消费种群是建筑产品的最终用户,消费者持续需求量是建筑绿色供应链管理和运作的动力。绿色建筑的价格、消费者剩余、环保理念等因素都会影响最终产品的消费绿色化。面对建筑的购买问题上,消费种群的策略集为Sy＝{购买,不购买}。当消费者有较强的绿色消费意识和购买能力时,人们则愿意购买绿色建筑参与绿色供应链的合作；绿色建筑的经济与生态效益体现具有长期性和整体性,在消费者对绿色性能的相关设计、未来效用感知不确定的情况下,消费者更愿意选择风险相对较小的传统建筑。回收加工企业在生态系统中是对废弃物进行加工再利用的分解种群,策略集为Sz＝{参与,不参与},选择接受表示参与绿色供应链,将上游施工过程、运营阶段和建筑物报废拆除中产生的建筑废弃物和装修废弃物进行加工处理；若企业不接受,则采用填埋、焚烧粗放方式处理垃圾。假设如下。

1.1 假设1:生产种群的相关损益

当开发商建设传统建筑的收益为Fs,成本为Cs；开发建筑绿色的额外收益为R＋ΔFs(R为品牌效应提升、销售增加等带来的经济效益,ΔFs指实施绿色供应链资源节约、废物处理费用减少带来的效益),需要承担的增量成本为kθ2(建设成本是绿色水平θ的增函数,同时随着绿色水平的提高,投入成本的边际效用是递减的)。

1.2 假设2:消费者种群的相关损益

消费者购买传统建筑的收益为Fe,成本为Ce；购买建筑绿色的增量收益为Gθ-R＋ΔFe,其中,G为消费者偏好系数,R为消费者购买绿色开发商的建筑产品所付出的增量成本(消费者的增量成本全部转为生产者的增量收入),ΔFe为消费过程中节水节能、绿色回收带来的经济收益以及健康环保的居住环境带来的长期收益,这部分可以表示消费者剩余,取决于主观效用价值。通常情况下建筑业供应链成员的信息并不对称导致消费者成为建筑产品的被动接受者,Cds为生产种群不开发绿色建筑时给绿色消费种群带来的损失。

1.3 假设3:分解种群的相关损益

生产者、消费者和分解者合作时的收益系数分别为Sop和Srp,回收企业的收益与其绿色分解能力(吸收能力)d成正比,则(Sop＋Srp)d表示博弈三方参与逆向物流分解种群的收益。Cp'和Cp分别为处理废弃物过程加工工艺改进和填埋焚烧所花费的成本。Cdp和Crp分别为回收企业不参与建筑绿色供应链合作给生产种群和消费种群带来的损失。

1.4 假设4

在建筑市场中,参与主体的行为总能对社会其他经济主体产生影响,包括环境效应、产业规模效应、社会效应等。所以,假设生产种群2种策略下所产生的正外部性的概率为βs1和βs2,对应的收益分别为ms1和ms2(βs1ms1＞βs2ms1),消费种群的正外部性概率 为βe1和βe2,对 应 的 收 益 分 别 为me1和me2(βe1me1＞βe2me2),分解种群接受和不接受的正外部性概率为βp1和βp2,收益分别为mp1和mp2(βp1mp1＞βp2mp2),分别用贴现因子λi(i＝a,b,c)将外部效应的未来收益进行量化,λi越大意味着参与者在采取行动时对未来利润和环境保护的重视程度越高,越有可能从长远利益出发参与建筑绿色的供应链。为了方便计算将其形式简化为Uij＝βijmij(i＝s,p,e；j＝1,2)。

基于以上假设可得三方主体的8种策略组合收益矩阵如表1所示。

表1 生产种群、消费种群和分解种群三方博弈收益矩阵

2 动态博弈模型及稳定性分析

在博弈论过程中,各参与方都是有限理性的且具有不完全信息性,不可能在一开始博弈中就能找到最优均衡点。但是主体具有学习模仿能力,可以在每轮博弈中通过学习比较同类主体策略收益来调整自身的策略,最终使各方主体形成演化均衡。因此,基于上述静态博弈模型支付矩阵,进一步对三者的决策行为进行分析。

2.1 生产种群复制动态方程及稳定性分析

生产种群开发建筑绿色的复制动态方程:

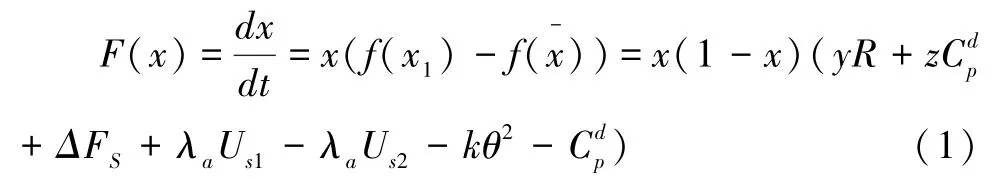
由全微分方程局部程稳定性定理可知,作为稳定策略的x应满足F(x)＝0且F(x)'＜0,令y*＝

当y＝y*,则F(x)≡0,此时生产种群中任何比例的“开发绿色建筑策略”群体都是均衡策略。

当y≠y*,令F(x)＝0,得到x＝0或1为2个均衡点。对F(x)求导得:

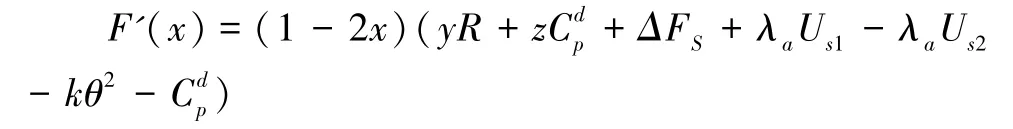
若λaUs1-λaUs2＞kθ2＋Cdp,y*＜0,y＞y*恒成立,则F'(x)｜x＝0＞0,F'(x)｜x＝1＜0,x＝1是稳定策略。尽管生产绿色建筑、参与绿色回收会增加开发成本,但是只要企业在对绿色建筑产品未来外部性收益持乐观预期的情况下仍会开发绿色环保的建筑产品。

若λaUs1-λaUs2＋ΔFs＋R＜kθ2＋Cdp-ZCdp,y*＞1,y＜y*恒成立,则有F'(x)｜x＝0＜0,F'(x)｜x＝1＞0,x＝0为稳定均衡点说明建筑企业开发绿色建筑的增量收益小于增量成本和回收企业带来的风险时,开发商倾向不开发绿色建筑。

若λaUs1-λaUs2＜kθ2＋Cdp-ZCdp＜λaUs1-λaUs2＋ΔFs＋R,0＜y*＜1,可分为以下2种情况:当y＞y*时,可得F'(x)｜x＝0＞0,F'(x)｜x＝1＜0,x＝1是稳定策略,生产种群选择开发绿色建筑。

当y＜y*时,F'(x)｜x＝0＜0,F'(x)｜x＝1＞0,x＝0时稳定策略,生产种群选择开发传统建筑。该情况说明生产种群的绿色建筑开发策略的进化稳定状态与消费种群、分解种群的决策密切相关,开发商选择何种策略是三方博弈的结果。

2.2 消费种群复制动态方程及稳定性分析

消费种群购买绿色建筑的复制动态方程:

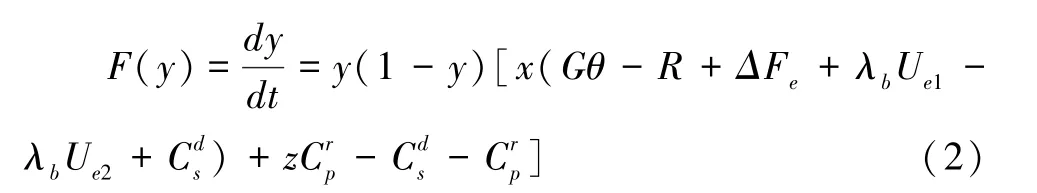
当x≠x*,令F(y)＝0,得到y＝0或1为2个均衡点。对F(y)求导得:

F'(y)＝(1-2y)[x(Gθ-R＋ΔFe＋λbUe1-λbUe2

若Gθ-R＋ΔFe＋λbUe1-λbUe2＜Crp-ZCrp,x*＞1,x＜x*恒成立,则有F'(y)｜y＝0＜0,F'(y)｜y＝1＞0,y＝0为演化稳定均衡点,即消费者节能环保行为获得的消费者剩余小于超额支出的成本时,无论生产者是否开发绿色建筑,消费者都选择传统建筑。

若Crp-ZCrp＜Gθ-R＋ΔFe＋λbUe1-λbUe2,0＜x*＜1,可分为以下2种情况:当x＞x*时,可得F'(y)｜y＝0＞0,F'(y)｜y＝1＜0,y＝1是稳定策略,经过一段时间的演化,消费种群全部转化为购买绿色建筑。

当x＜x*时F'(y)｜y＝0＜0,F'(y)｜y＝1＞0,y＝0是稳定策略,消费种群将倾向于演化为不购买绿色建筑产品。因此,在消费者在消费绿色建筑产品能满足其心理需求,同时也能通过节约资源获得更多经济效益的情况下,消费是否购买绿色建筑的行为决策演化方向更多的取决于开发商的供给能力。

2.3 分解种群复制动态方程及稳定性分析

分解种群参与建筑绿色供应链的复制动态方程:

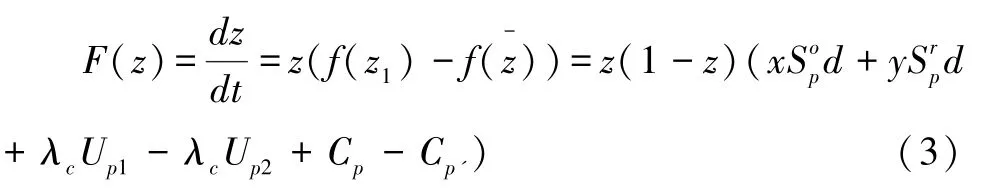
当y≠y*,令F(z)＝0,得到z＝0或1为2个均衡点。对F(z)求导得:F'(z)＝(1-2z)(xSopd＋ySrpd＋λcUp1-λcUp2＋Cp-Cp')

若Cp-Cp'＞0,y*＜0,y＞y*恒成立,则有F'(z)｜y＝0＞0,F'(z)｜y＝1＜0,z＝1是演化稳定均衡点。说明在分解种群分垃圾资源化技术水平的提高,采用传统方式处理建筑垃圾的成本会高于绿色回收的成本投入的情况下废弃物处理企业倾向选择绿色环保处理模式。

若Cp'-Cp＞λcUp1-λcUp2＋Srpd＋xSopd,y*＞1,y＜y*恒成立,则有F'(z)｜z＝0＜0,F'(z)｜z＝1＞0,z＝0是演化均衡点。说明分解种群在参与建筑废弃物的资源回收带来的收益不足以中和企业绿色转型的成本的情况下,更倾向于选择直接焚烧填埋的模式。

若0＜Cp'-Cp＜λcUp1-λcUp2＋Srpd＋xSopd,0＜y*＜1,可分为以下2种情况:当y＞y*时,可得F'(z)｜z＝0＞0,F'(z)｜z＝1＜0,z＝1是稳定策略,说明选择购买建筑绿色的消费者达到一定规模,由于进行废弃物再生的经济效益明显,分解种群最终演化策略趋向于参与建筑供应链中。

当y＜y*时,F'(z)｜z＝0＜0,F'(z)｜z＝1＞0,z＝0时稳定策略,说明消费者购买建筑绿色的数量逐渐减少,分解企业可能很难获得具有回收利用价值的建筑废弃物,因此废弃物处置企业会选择直接掩埋焚烧的方式。

2.4 三方主体演化策略稳定性分析

在非对称博弈中,演化博弈均衡点E一定是纯策略均衡,因此只需分析纯策略E1(0,0,0),E2(0,1,0),E3(0,1,1),E4(0,0,1),E5(1,0,0),E6(1,0,1),E7(1,1,0),E8(1,1,1)这8个点的渐进稳定状态。稳定性的分析可以通过李雅普诺夫判别法(间接法)进行判定,上述微分方程系统的雅可比矩阵如下:

由李雅普诺夫第一法则可知,当雅可比矩阵所有特征值λ＜0,该均衡点是渐进稳定点,即为汇；当所有特征值λ＞0时,该均衡点是不稳定点,即为源；当特征值λ存在正负时,该均衡点是不稳定点,即为鞍点。求其行列式的特征值稳定性结果如表2所示。

由表2可知,生产种群、消费种群和分解种群三方博弈策略动态演化趋势,可成为本文演化稳定策略的是E1(0,0,0)E4(0,0,1)E5(1,0,0)E7(1,1,0)E8(1,1,1)。在发展起步阶段自然推荐状态下由于信息的缺乏、市场的封闭、风险的不确定性、政府引导不力因素的影响,建筑绿色供应链参与主体利益不能得到保证的情况下,构成稳定的策略组合为(不开发,不购买,不参与),任何一方都没有改变自己行为的动力；当生产种群对建筑的绿色适应水平、维护能力、技术积累不断提高导致成本减少,同时政府的政策支持使绿色建筑的正外部性内化程度不断提高,则开发绿色建筑的经济利润逐步提高,传统建筑的经济利润减少弥补了市场失灵的缺陷,然而随着时间的演进,当生产种群、消费种群和分解种群参与供应链的收益大于其不合作的收益时,部分选择非绿色行为的主体在下一轮博弈中将转而选择绿色节能行为,经过多轮博弈,系统最终收敛到演化均衡点(开发,购买、参与)的博弈局势,这个是政府部门和社会所期待的良性结果。

表2 均衡点的稳定性分析

3 仿真模拟及结果分析

为更加直观展现三方均积极采取策略的理想状况下系统演化路径情况,参考徐建中[11]文章中构建的三主体演化博弈模型仿真思路,采用数值实验和MATLAB仿真的方法对以上设想进行验证。使初始参数设定需满足的演化条件:

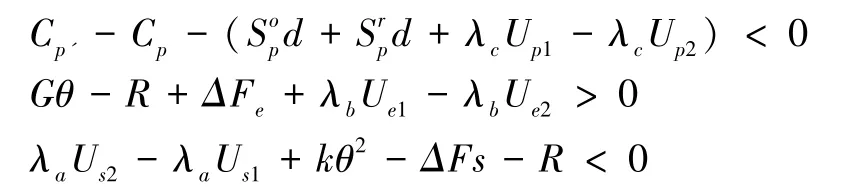
根据前文分析,当λaUs2-λaUs1＋kθ2-ΔFs-R＜0时,可得y＞y*,F'(x)｜x＝0＞0,F'(x)｜x＝1＜0,x＝1是稳定演化路径,即生产种群会参与建筑供应链的建设环节,开发绿色建筑。生产种群的行为选择会随着分解种群概率的变化而变化,当分解种群参与建筑供应链的回收分解环节的概率越大,生产种群参与的概率也越大。因此,可以使y*＝尽可能的小,即需要提高生产种群的外部性收益和绿色增量收益,降低绿色增量成本。

当Gθ-R＋ΔFe＋λbUe1-λbUe2＞0时,可知x＞x*,F'(y)｜y＝1＜0,y＝1是稳定策略,即消费者种群会选择参与绿色建筑供应链的运营环节,选择购买绿色建筑。因此需要使可能地小,即需要提高消费者的未来价值感知,提高消费者剩余。

当Cp'-Cp-(Sopd＋Srpd＋λcUp1-λcUp2)＜0时,可知y＞y*时,可得F'(z)｜z＝1＜0,z＝1是稳定策略,即分解种群会选择参与建筑供应链的分解回收环节。因此,需使尽可能地小,则需要提高分解种群的外部收益,增强资源回收的能力,密切分解种群和上游生产种群、消费种群的联系。

通过上述分析可知,均衡点(1,1,1)随着三者的稳定条件的变化情况,接下来给出如表3初值设定,用MATLAB进行数值模拟,验证在满足初始条件情况下,混合策略的演化路径。

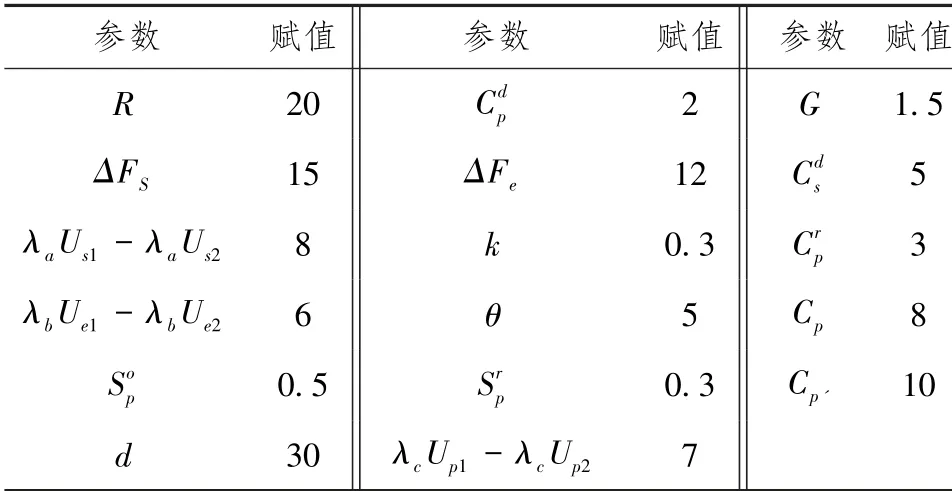
表3 参数赋值表

在以上条件下,当固定x的初值x＝0.5,通过MATLAB随机选取16组y、z的策略组合,可得到在y和z的初值变化下任意变化情况下,x随时间t的变化情况,见图2。表明在满足理想条件的情况下,x的演化规律是单调递增且最终趋近与1,这说明在开发绿色建筑的增量收益大于绿色增量成本时,生产者种群开发建筑绿色的人数会持续上升并且全部都会选择开发绿色建筑。图2表明,在保持演化条件不变的情况下,x值随时间变化是呈单调递增的取值,并且不会因y和z比例的变化而改变自己的策略。

图2 y和z变化时x值演化曲线图

图3验证了在变动x和z比例时,y值动态演化呈现的规律。通过固定y的初始值y＝0.5,得到y值的变化曲线。表明消费者对生产者的购买比例和回收企业的参与呈非单调性,但其演化最终趋势仍是全部购买绿色建筑产品和参与回收。在演化过程中,很可能出现消费者购买绿色建筑和回收大幅度下降的情况。这说明,消费者了解和接受绿色产品、树立废弃物资源化利用意识都需要一个过程,开发商和回收企业要以乐观积极的态度看待给予消费者一定时间转变自己的消费观念。图4验证了在变动x和y的初值,得到z值的变化曲线。

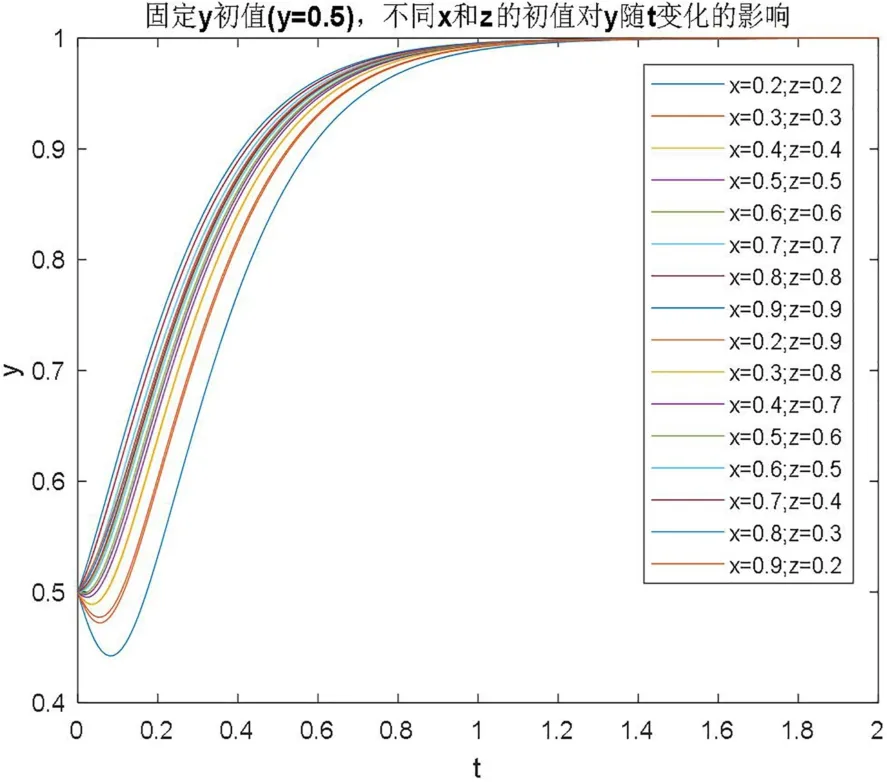
图3 x和z变化时y值演化曲线图

图4 x和y变化时z值演化曲线图

通过以上算例实验和仿真,在满足初始条件下,3个博弈主体均可以随时间单独演化到全部采取积极策略。如图5所示,分别以初始x＝0.4,y＝0.4,z＝0.2；x＝0.4,y＝0.3,z＝0.7；x＝0.6,y＝0.4,z＝0.3为例,演示3个博弈主体的策略选择在一个三维坐标中的演化趋势,仿真结果表明,以上条件可以使三方主体最终演化至(1,1,1)的理想稳定状态,充分验证了前文推断趋于稳定状态条件的可靠性。

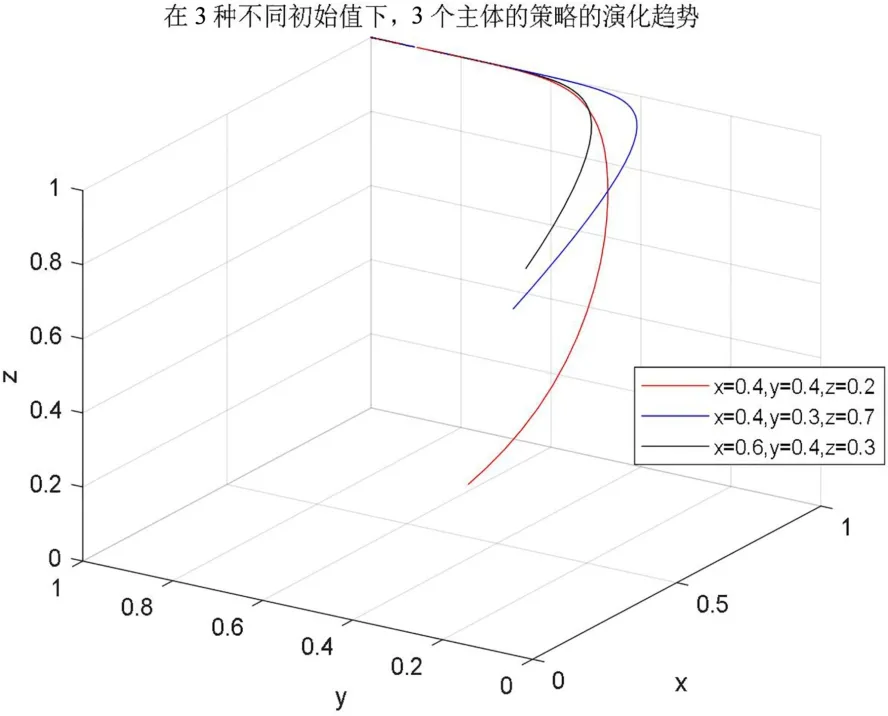
图5 三方博弈系统演化路径图

4 结论

立足建筑绿色供应链生态系统的背景下,本文构建了生产种群、消费种群、分解种群三方主体绿色行为决策的演化博弈模型,通过分析三方的决策行为随时间的动态演化过程,得到如下结论。

在建筑绿色供应链的构建中,生产种群、消费种群、分解种群3个主体的决策行为之间是相互影响的,即生产种群选择“开发”策略的概率与消费种群“购买”的比例和分解种群选择“参与”的比例有关；同样地消费种群选的“购买”比例也与其他两主体的选择策略相关；分解种群选择“参与”的比例也与其他两主体的策略选择有关。这表明建筑绿色供应链的构建的稳定性影响因素是复杂且多方面的,三主体的行为决策不仅仅需要考虑自身的利益,还需要通过其他主体的行为决策才能做出判断。

消费种群转变消费观念,树立健康环保的意识需要一个过程,在演化初期,会出现消费种群购买绿色建筑、参与绿色回收的比例大幅度减小的情形。因此,企业需要提高建筑绿色的相关技术(包括绿色建材的使用、建筑绿色设备推广、BIM等信息技术的支持),降低绿色建筑的价格。同时,利用各类媒介加强对绿色建筑的宣传推广,为消费者提供更多绿色建筑的信息,减少信息不对称的负面影响。政府也要采取措施将建筑绿色的环境效益内部化,增强消费者对绿色建筑的未来价值感知,促进消费者选择购买绿色建筑。

当初始条件满足R＋ΔFs＋λaUs1-λaUs2＞kθ2,Gθ-R＋ΔFe＋λbUe1-λbUe2＞0,Sopd＋Srpd＋λcUp1-λcUp2＞Cp'-Cp时,才可以推动绿色供应链的有效实施。具体来说,三方最终会采取哪种策略组合收敛于稳定状态取决于生产者种群的增量收益、绿色增量成本；消费种群的绿色消费偏好、增量收益和未来价值感知；分解种群的分解能力、分解成本和合作收益系数。

总之,建筑绿色供应链将可持续发展的理念及供应链思想相融合,使得贯穿于建筑全生命周期内各主体的活动要与环境相容,达到对环境负影响最小的目的,促进经济与环境的和谐发展。本文介绍了建筑绿色供应链系统的社会系统、生产系统、消费系统、回收系统4大系统,在此基础上建立了有限理性前提下建筑绿色供应链生产种群、消费种群、分解种群三方演化博弈模型,运用复制者动态方程分析参与各方进行复制动态及演化稳定均衡,进而探寻不同情况下各参与主体的行为选择,并进一步用MATLAB对满足(1,1,1)理想状况下的有效条件进行详细分析。