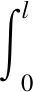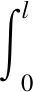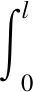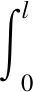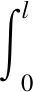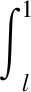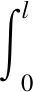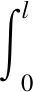退化抛物型方程扩散系数识别的反问题

许 瑶 瑶

(兰州交通大学 数理学院，甘肃 兰州 730070)

0 引言

我们研究两种退化抛物型方程的扩散系数识别的反演问题,主要讨论一维线性方程.当0<α<1时,弱退化方程如下:

(1)

当1≤α<2时,强退化方程如下:

(2)

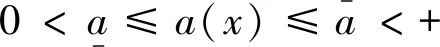
考虑并分析以下两种类型的未知扩散系数识别的反演问题.

线性情况:给定α=1,反问题是根据在某一时刻的附加数据来识别常数系数a(x)≡a的,其中a是未知的正常数.

幂指数型情况:给定a(x)=1,反问题是根据在某一时刻的附加数据来识别幂指数α∈(0,2)的.

近年来,退化抛物型方程由于其重要的相关理论分析和实际应用而受到越来越多的关注,如气候学[1]、种群遗传学[2]、金融数学[3]、流体动力学[4]等.反问题是一种在Hadamard意义上不适定的问题[5-6],这意味着,要么解不存在,要么解不唯一,或者观测数据的小误差可能会导致解的计算出现巨大误差.而对于讨论解的唯一性和稳定性的理论方法主要包括:能量方法和Hardy不等式,强极值原理[7],Laplace积分变换和其他类似的积分变换方法,以及Carleman不等式.

退化抛物型方程反问题具有重要的基础意义和实际应用.期权定价中著名的Black-Scholes方程:

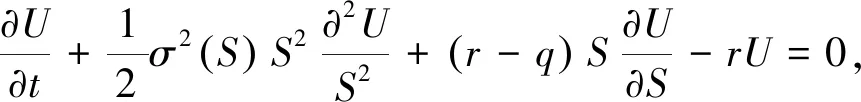
就是一个退化抛物型方程,很显然s=0是它的退化边界.文献[8]研究了利用市场观测数据重构隐含波动率σ的反问题.文献[9]考虑退化抛物型方程的唯一延拓和近似能控型:

Lu:=ut+(xαux)x,Q=(0,1)×(0,T)，

边界条件为u(0,t)=(xαux)(0,t)=0.推导出L新的局部Carleman估计得到唯一的延拓性结果并推导出弱退化问题的Dirichlet边界控制的近似可控性;文献[10]运用压缩映射原理和基于预测-校正方法的数值算法分析了退化抛物型方程一阶系数的反演问题;文献[11]基于最优控制理论来反演一类退化热传导方程中的与空间相关的热源.

我们注意到对于确定非退化抛物型方程的电导率和辐射系数等空间变化系数的反问题已有大量的工作[12-13]；但大多数用于处理非退化抛物方程的方法不再适用于退化的情况,一般会将退化抛物型系数反演问题重新表述为极值问题,这是当今经典的方法并且已经在许多情况下得到应用[14-15].

本文结构如下，第一节中,我们考虑正问题(1)和(2)的解的适定性;第二节第一部分使用能量方法证明了线性情况下常数系数a的Lipschitz稳定性和唯一性结果;第二节第二部分将专门讨论幂指数型情况下识别(1)和(2)中的α.同样,幂指数α的Lipschitz稳定性和唯一性将通过能量方法得到有效证明.

1 预备知识

本节中,我们将考虑与(1)和(2)有关的正问题的适定性.对于任意的l>0,令H=L2(0,l),对于α∈(0,2),我们考虑以下函数空间:

(3)

和

0<α<2.

现在将经典的庞加莱不等式应用于上述加权空间.

定理1(庞加莱不等式) 对于所有的ε>0,存在一个常数Cp=Cp(ε,l)>0，使得对所有的α∈[0,2-ε],以下不等式成立:

(4)

证明因为l>0是给定的,考虑以下两种情况.

①假设α=1对于所有的x∈(0,l),有

因此,得到

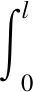
②假设α≠1且α<2,有

因此,有

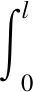
定理1得证.

(5)

问题(1)和(2)可以用抽象的形式重新表述

(6)

通过引入线性算子A:D(A)⊂H→H定义为

(7)

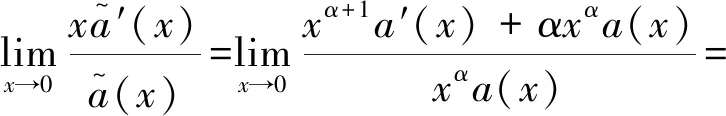
(8)

因此可以通过文献[16]得到(6)和非齐次问题(9)的适定结果

(9)

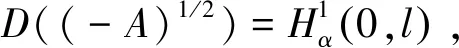
定理2[16]假设(5),那么A是强连续收敛半群etA的无穷小生成元.而且etA是可解析的.因此对于任意的u0∈H,问题(6)的解u(x,t)=(etAu0)(x)满足:

(i)u∈C([0,∞);H),

(iii)u(t)∈∩n≥1D(An)，∀t>0.

此外,如果u0∈D((-A)1/2),那么对于任意的f∈L2(0,T;T)，则问题(9)有弱解

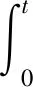
注u(t)∈H1(0,T;H)∩C([0,T];D((-A)1/2))∩L2(0,T;D(A))且对于几乎所有的t∈[0,T],u(t)满足(9)中的方程.

2 通过能量方法重构

2.1 线性情况: 唯一性和Lipschitz稳定性

(10)

当a=ai时,令ui,i=1,2是(10)的解,也就是说

(11)

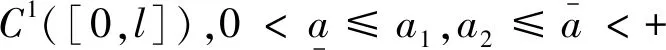
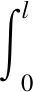
(12)

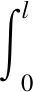
证明假设a2≥a1,令w=u1-u2.则

∂tw+c(x)w-a1∂x(x∂xw)=(a1-a2)∂x(x∂xu2),

两边同乘u2并分部积分,我们得到

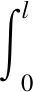
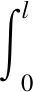
又因为c(x)是有界函数且c(x)≤m,则

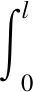
显然,由上述定理的证明,可以推导出下列唯一性结果.

2.2 幂指数型情况:唯一性和Lipschitz稳定性

本节中,我们考虑退化抛物型方程(1)和(2)中的幂α的反问题.首先为了简单起见，令a(x)≡1和f≡0,则方程(1)和(2)可分别改写为:弱退化方程(0<α<1)

(13)

和强退化方程(1≤α<2)

(14)

在这一节中，我们分析(13)和(14)中幂α的唯一性和稳定性,从唯一性结果开始分析.

定理4假设0

证明为了不失一般性,假设α1<α2,设w(x,t)=u2(x,t)-u1(x,t)，则

∂tw+c(x)w-∂x(xα2∂xw)=
∂x((xα2-xα1)∂xu1),

(15)

两边同乘u1并分部积分,得到

(16)

由假设可知，存在t0∈(0,T]，使得∂tw(·,t0)=w(·,t0)=0.那么,由式(16)有

又因为对于所有的x∈(0,l),有xα1>xα2,通过上式可得，对于几乎所有的x∈(0,l)，

∂xu1(·,t0)=0.

利用抛物型方程逆时问题解的唯一性，可知u0=0,与定理假设矛盾.故α1=α2.定理4得证.

定理5(Lipschitz稳定性)假设00，

(17)

那么存在一个正常数C=C(ε,l,m)>0使得

其中α1∨α2=max{α1,α2}.

注定理5中，假设0

首先,令w(x,t)=u2(x,t)-u1(x,t).通过式(15)和(16),我们观察到

另一方面,有

(18)

下面,通过式(16)知，

故由庞加莱不等式(4)，可以得到

则由式(18)和(19)可知

则定理5成立.