生猪疫情冲击下猪肉价格预测与风险预警研究*

花俊国，苏贵芳，贾云飞

（河南农业大学经济与管理学院，郑州 450046）

一、引言

猪粮安天下。猪肉在我国的“菜篮子”工程中占有非常重要的地位，是居民必需的肉类消费品，占肉类总需求的60%～70%，决定着居民的“肉盘子”。养猪业由此成为我国肉类食品安全的基础性产业和战略性产业，在三农领域中占比较大，其稳定发展对于居民生活及社会大局稳定具有重要作用。但近年来，生猪疫情频发，继2009年的猪肺疫、猪丹毒以及2011～2012年的猪口蹄疫爆发后，2018年非洲猪瘟爆发又对猪肉市场造成极大不利影响，猪肉价格呈现“过山车”式波动（陈昱帆等，2022）。为此，国家密集出台各项扶持政策促进生猪产能恢复，防止猪肉价格持续高涨。2020年中央一号文件提出要全力做好生猪稳产保供工作，在经历了2020年生猪生产恢复的艰巨任务后，当前猪肉保供稳价基础仍不牢固，猪肉价格管控也一直受到国家的高度重视。2021年中央一号文件指出要“保护生猪基础产能，健全生猪产业平稳有序发展的长效机制”，国家发展和改革委员会对生猪及猪肉价格坚持“调高”与“调低”并重，将政府储备猪肉的调节作用作为关键抓手。

在各种不确定事件频发的背景下，猪肉市场发展所面临的风险挑战增加，猪肉价格波动形势更是复杂多变。“价高伤民，价贱伤农”，猪肉价格的过度波动对居民正常生活与经济社会稳定带来较大威胁。特别是2018年非洲猪瘟爆发给我国猪肉市场带来严重创伤，造成猪肉价格波动频率增加、波动幅度增强，价格风险增大。非洲猪瘟等重大外部冲击事件除了直接影响市场外，还将扰乱猪肉价格的周期运行规律，使猪肉价格产生非常规性波动，进一步造成生猪养殖者盲目决策，如恐慌性出栏、积极补栏或大量养殖者进入市场等行为，导致生猪产业链恶性循环危害整个产业稳定发展。

目前，在政府干预和市场配置的共同作用下猪肉价格已出现回落，但价格暴涨是否会引发产能过剩的“疫情后遗症”？猪肉价格是否会出现“断崖式”下跌？后疫情时期，生猪产能加速恢复，猪肉市场可能面临新的风险挑战，猪肉价格波动问题仍需给予高度关注。考虑多种因素准确预测猪肉价格有助于猪肉市场的参与者合理决策，避免因非理性决策带来市场紊乱，进而对生猪产业链造成更严重冲击（苏贵芳等，2021）。鉴于此，本文将生猪疫情纳入猪肉价格预测模型，把握生猪疫情冲击下的猪肉价格变化趋势，并在此基础上进行风险预警研究，以期为政府相关部门、生产者和消费者制定前瞻性和科学性决策提供参考依据。

二、文献综述

现有研究越来越重视未来农产品市场的发展趋势和风险管理，农产品市场风险主要来源于农产品价格波动（赵瑞莹等，2004）。猪肉价格作为我国农产品价格体系的重要标尺，其风险管理对于稳定农产品价格至关重要。全面考虑猪肉价格波动因素，准确把握猪肉价格波动趋势成为学者研究的焦点。猪肉产业链主要包括饲料供应、生猪养殖、生猪屠宰、猪肉加工及销售等环节，较多的生产环节形成了较长的产业链，使猪肉价格更易受到供、需等多重因素影响（熊涛，2021）。许彪等（2014）认为趋势因素、周期因素、季节因素、偶发因素、货币因素是影响猪肉价格的五大因素，偶发性因素会导致猪肉价格产生非常规性波动，严重时会扰乱周期运行。毛学峰等（2008）同样认为生猪价格周期会受外部冲击影响，外部冲击加剧了供需矛盾，对生猪价格波动具有推动作用。疫病等不规则因素会引起供求失衡，从而导致猪肉价格短期内大幅波动（于少东，2012）。由此可见，突发性事件的冲击是引发猪肉价格短期内剧烈波动的重要因素，在猪肉价格风险管理中应给予高度关注。

猪肉价格作为猪肉市场发展的指向标，是价格风险管理的关键，因此猪肉价格预测问题受到学者广泛关注。Saengwong等（2012）运用ARIMA模型和方差分解方法对生猪价格进行短期预测。Molina等（2017）运用X-12 ARIMA模型对菲律宾猪肉价格波动趋势进行分析，发现猪肉价格具有季节性波动特征，这种季节性波动是可预测的。Andres等（2018）认为，采用时间序列模型对猪肉价格预测大多存在没有考虑市场风险的缺陷，故其预测精度较差。国内有学者采用时间序列预测法、单一预测模型、组合模型及机器算法等对猪肉价格进行预测。李苏等（2020）通过Census X12季节调整模型发现我国猪肉月度价格呈明显的季节性波动特征，并进一步采用ARMA模型预测猪肉价格。罗创国等（2010）采用ARIMA模型预测生猪季度价格，发现ARIMA模型对我国生猪价格预测效果较好，可以准确预见生猪价格短期波动情况。吴培等（2019）也发现ARIMA模型适合短期预测，预测误差随着预测周期延长而变大，而GM模型的预测结果普遍被高估，适合中长期预测，预测误差随着预测周期延长而变小，ARIMA-GM-RBF模型综合了二者的优点，预测结果的相对误差最小，拟合效果最好。

随着信息技术发展，机器学习被广泛应用于各个领域，基于多维数据挖掘分析数据的潜在规律对于准确预测价格波动趋势具有重要作用。BP神经网络和SVM模型是被广泛用于价格预测研究的机器学习方法。BP神经网络被用于大豆（王川等，2008）、鸡蛋（高扬等，2021）、油菜（吴清华等，2010）等农产品的价格预测研究。猪肉价格影响因素众多，单一变量难以准确预测猪肉价格变化趋势，引入数据挖掘从多维数据中提炼信息准确把握猪肉价格非常必要（马再兴，2019）。已有研究考虑生产、市场、供给、需求等因素的同时，将生猪疫病指标纳入生猪市场价格预警体系，运用BP神经网络模型对未来生猪市场价格进行预测及预警（刘芳等，2013）。Hamm等（1997）发现神经网络模型预测生猪月度价格的效果优于ARIMA模型。付莲莲等（2017）建立BP神经网络对生猪价格波动进行预警分析，模型输出的预警值与实际值较为相近，预测警度和实际警度也基本一致。但丁琳琳等（2012）发现支持向量机（SVM）对生猪价格的模拟效果和预测精度均优于BP人工神经网络模型。SVM被广泛应用于股市研究中（夏爽，2019；吕子夷，2020），李优柱等（2014）从自然环境、经济与政策环境、供给、需求等方面设置29个指标，采用多种方法从众多指标中综合提取特征指标，建立SVM模型对蔬菜价格预测预警分析，其预测精度较高。此外，SVM最终转化为二次寻优问题，可避免神经网络等其他机器学习算法易陷入局部极值的问题。

综上所述，关于农产品价格预测的研究较为丰富，这些研究为预测指标体系的设立和研究方法的选取提供了丰富的基础，但仍有一定拓展的空间。一方面，由于近年来生猪疫情频发，猪肉价格变化的影响因素错综复杂，仅基于单一时间序列数据而不考虑市场风险预测猪肉价格存有一定缺陷。另一方面，一些研究虽考虑了多方面因素，但指标设计不够全面。猪肉价格具有非线性和非平稳的特点，通过数据挖掘的方法引入多种指标进行猪肉价格的预测可信度及准确率较高，但因指标过多易产生冗余问题，造成维数灾难。鉴于此，本文从疫病、供给、需求、宏观经济环境四个方面考虑猪肉价格影响因素，构建猪肉价格预测指标体系，运用相关性分析、均方差分析和主成份分析选取特征指标建立基于支持向量机（SVM）的猪肉价格预测模型，并根据3σ原则设定猪肉价格波动警限，对猪肉价格波动进行风险预警。考虑多种因素对猪肉价格波动进行预测预警，不仅是对猪肉价格预测研究的有效补充，还为相关部门提供决策支持，对促进猪肉价格的平稳运行以及产业稳定健康发展具有重要意义。

三、猪肉价格预测指标体系的设置与评价

（一）猪肉价格预测指标体系的设置

猪肉价格波动受生猪产业链内部因素和外部环境因素的交叉影响，根据猪肉价格影响因素的相关研究（张敏等，2018），本文将猪肉价格预测的影响指标分为疫病、供给、需求和宏观经济环境四个方面，共包含33个指标（见表1）。供给和需求方面的指标主要为生猪产业链内部影响猪肉价格的因素，疫病和宏观经济为猪肉价格运行的外部环境。其中，选取生猪疫情宽度指数作为衡量生猪疫病爆发情况的代理变量，该指数可以综合衡量全国范围内生猪疫情爆发情况，主要从爆发范围、严重程度、传播速度等几方面量化打分综合得出。指标设置体系如表1所示，数据来源于国家统计局、前瞻数据库、布瑞克农业数据库。

表1 我国猪肉价格预测指标体系

（二）猪肉价格预测指标体系的评价

生猪疫情宽度指数自2009年2月公布，且2009年猪丹毒、猪肺疫、蓝耳病发生的次数较多，该年的生猪疫病情况较为严重，故研究的样本区间为2009年2月～2021年10月。本文先将生猪疫情宽度指数作为衡量疫病的特定指标输入模型，为避免指标冗余度的问题，对其他32个指标进行综合分析评价，最终提取特征指标输入模型。在提取特征指标的过程中，借鉴李优柱等（2014）在蔬菜价格预警时采用的数据处理方法，综合相关性分析、均方差分析和主成份分析三种方法，既考虑了数据的离散程度对价格预测的影响，又能体现数据相关程度在价格预测分析中的重要性。

1.相关性分析

相关性分析是指对两个或多个具备相关性的变量元素进行分析，从而衡量两个变量之间的相关密切程度。正相关和负相关在变量之间具有相同的影响效果，本文根据相关系数的绝对值进行排名。为使预测结果符合前瞻性标准，将所有影响指标均至少滞后1期，对猪肉价格与各影响指标进行相关性分析，结果如表2所示。由相关性分析结果可知，选取的影响指标大部分在1%水平上与猪肉价格显著相关，说明影响指标的选择较为合理，均与猪肉价格具有较强的相关性。

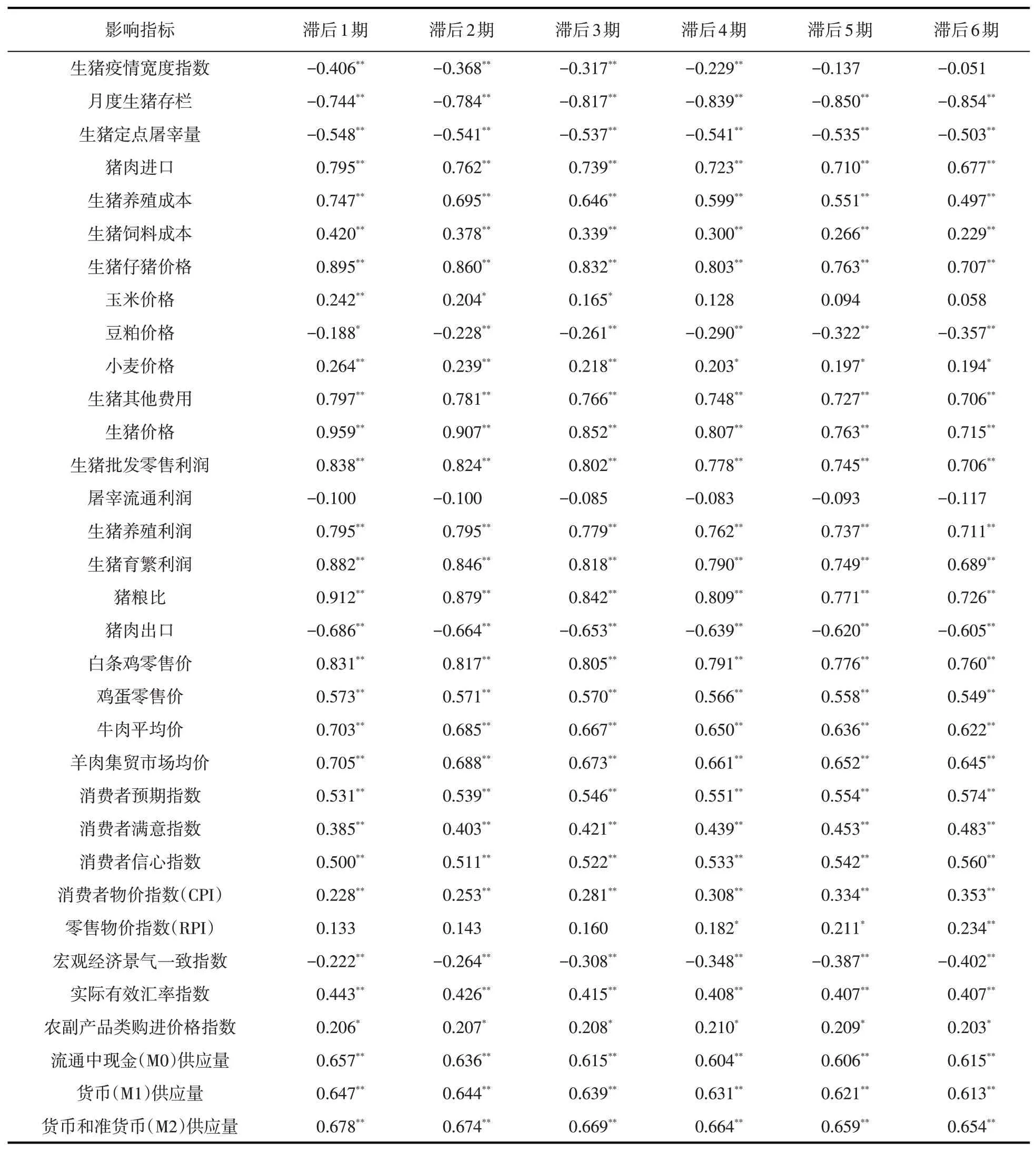
表2 相关性分析结果

2.均方差分析

鉴于生猪疫情宽度指数已作为特定指标输入模型，故需对其余32个影响指标进行均方差分析，均方差又称标准差，用σ表示，它是方差的平方根，指各数据偏离平均数距离的平均数，是离均差平方和平均后的方根，能反映一个数据集的离散程度。计算方式为：

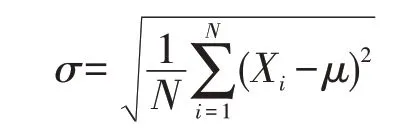
式中，Xi指某个样本数值，N指样本量，μ指这组样本数值的平均值。分别计算其余32个影响指标的均方差，结果如表3所示。

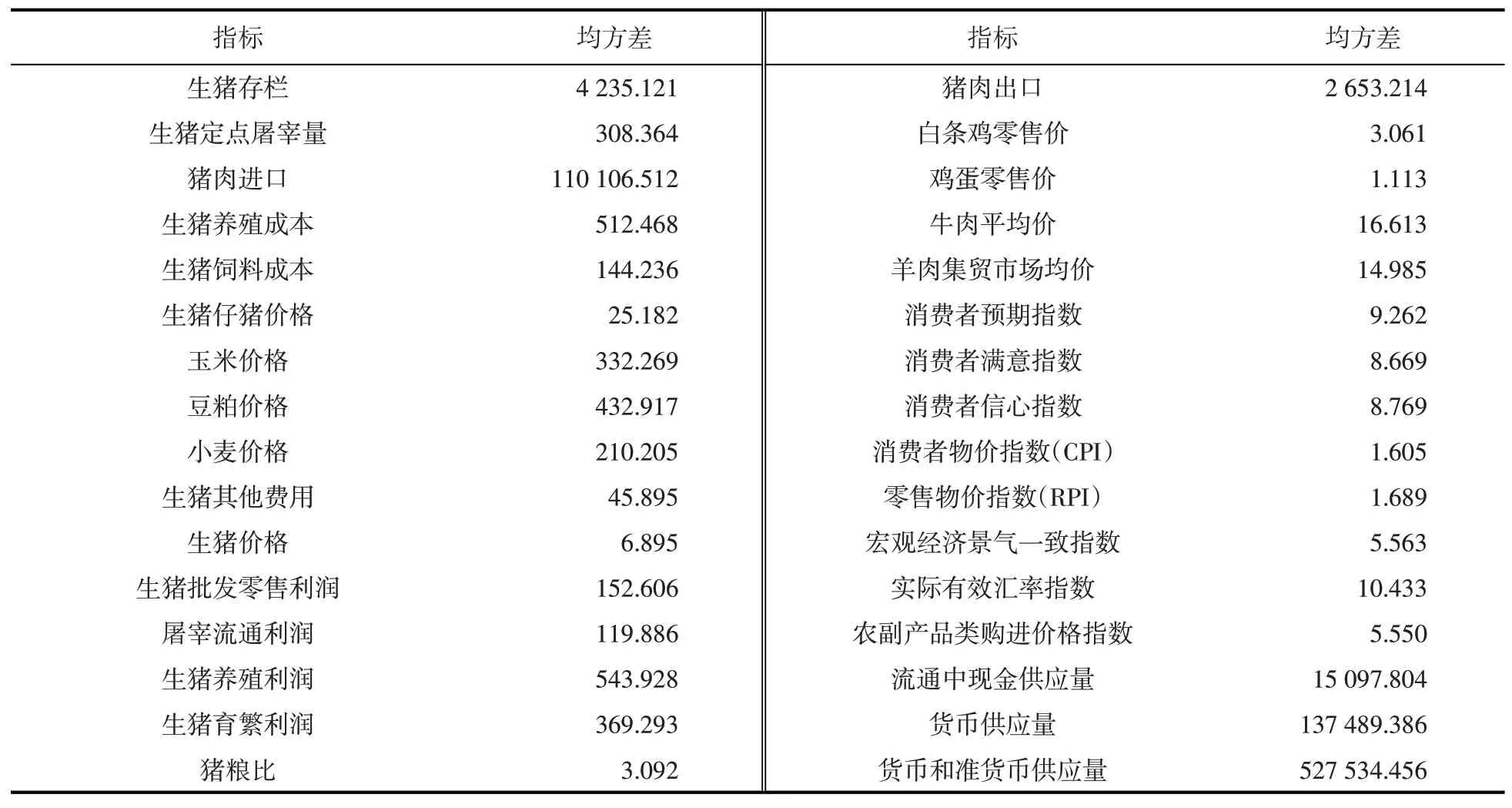
表3 均方差分析结果

3.主成份分析

主成份分析是被广泛使用的一种降维方法，目的是将高维数据投射到低维空间里。通过正交变换将一组可能存在相关性的变量数据转换为一组线性不相关的变量，转换后的变量被称为主成份。本文利用SPSS软件对除生猪疫情宽度指数外的影响指标进行主成份分析。

主成份分析结果中，从32个变量中共提取了5个主成份，根据主成份载荷表显示，大部分指标在第一主成份上载荷较大，即与第一主成份的相关系数较高。其中，第一主成份中载荷较大的指标有：白条鸡零售价、货币和准货币供应量、生猪其他费用、牛肉平均价、货币供应量、流通中现金供应量、猪肉进口、羊肉集贸市场均价、猪肉出口、生猪批发零售利润、生猪仔猪价格、生猪价格、消费者预期指数、生猪育繁利润、月度生猪存栏、消费者信心指数、生猪养殖成本、猪粮比、实际有效汇

率指数、消费者满意指数、鸡蛋零售价；第二主成份中载荷较大的指标有：农副产品类购进价格指数、CPI、小麦价格、生猪养殖利润、屠宰流通利润、生猪定点屠宰量；玉米价格、生猪饲料成本、豆粕价格在第三主成份上载荷较大；RPI在第四主成份上载荷较大；宏观经济景气一致指数在第五主成份上在载荷较大。由于样本量有限，采用主成份分析法从多维数据中提取相关程度高的指标，保证选取信息的代表性和有效性。

4.综合选取

本文综合以上三种指标选取的分析方法确定最终的特征指标。首先，根据相关性分析结果，按照相关性系数对所有指标进行排序。从相关性分析结果可以看出，屠宰流通利润与猪肉价格不存在相关性关系，农副产品类购进价格指数与猪肉价格仅在5%水平上显著相关（见表2），为保证所选影响指标与猪肉价格具有较强相关性，将二者剔除，不参与综合排名。因滞后1期的生猪疫情宽度指数与猪肉价格相关性最高，故将其作为疫病的最终衡量指标输入预测模型。其次，将每个影响指标的相关系数排名和均方差排名相加，得到综合排名，根据综合排名对各指标排序，综合排名如表4所示。最后，根据综合排名结果将五种主成份都考虑进去，由于第一主成份包含指标较多且综合排名较高，故第一主成份选取综合排名较高的月度生猪存栏和猪肉进口，结合相关性分析结果，滞后期数确定分别为滞后6期和滞后1期。第二主成份选取滞后1期的生猪养殖利润。第三主成份选取滞后1期的豆粕价格。第四主成份选取滞后6期的宏观经济景气一致指数。第五主成份选取滞后6期的RPI。

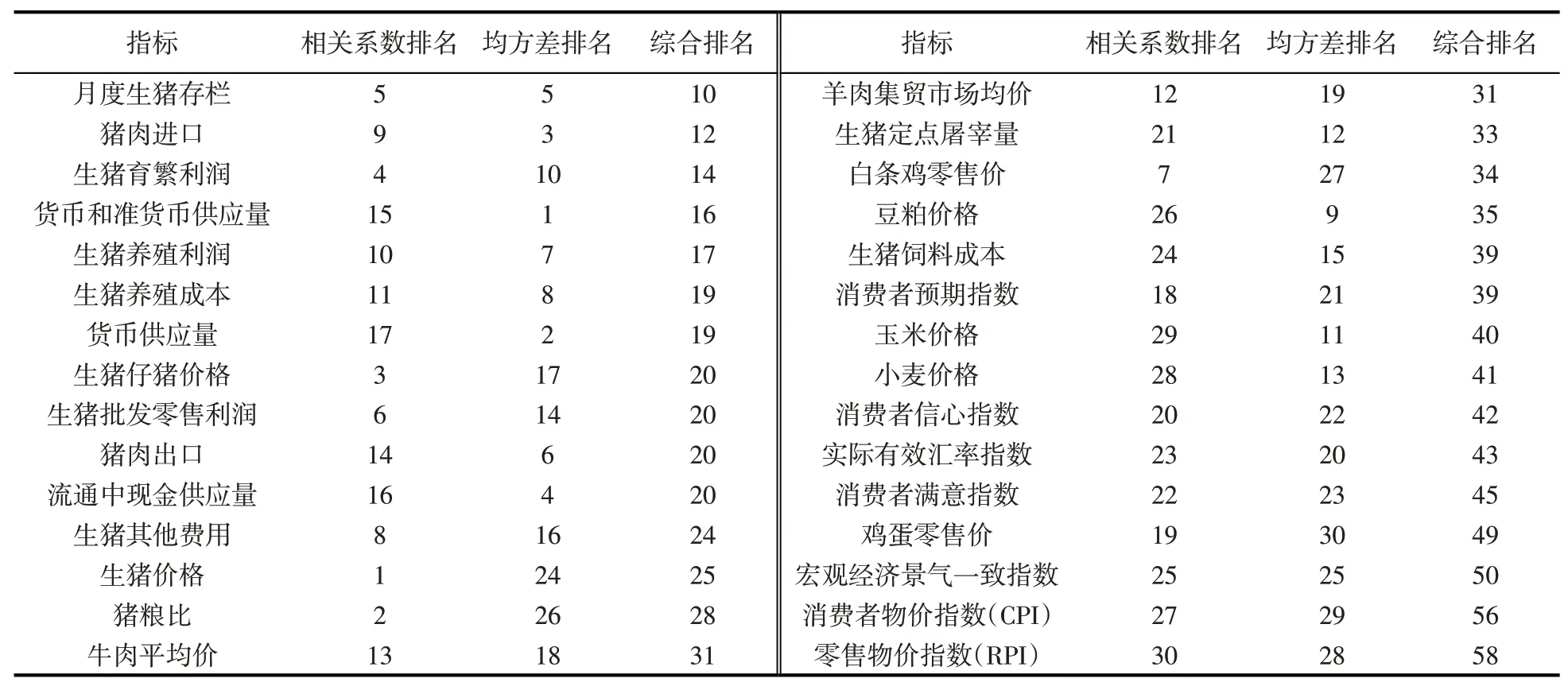
表4 综合选取法指标排序

四、支持向量机模型

支持向量机（Support Vector Machine，简称SVM）是1995年由Cortes和Vapnik提出的一种建立在统计学习理论基础上的机器学习算法。SVM的基本思路是：首先建立了一个具有一定规则的模型，然后借助该模型对已知数据进行学习和训练从而探究数据之间关联性，最后根据训练的模型预测未知数据，这是一种尽可能反映事物本质的学习方法（向昌盛，2011）。SVM是主要针对有限样本数据进行学习、分类和预测的一种方法，通用性强、鲁棒性高，相较神经网络模型具有更好的泛化能力（汪海燕等，2014）。因此，本文选择SVM模型进行猪肉价格的预测与风险预警研究。

SVM分类器的学习目标是在n维数据空间中找到一个超平面，可表示为：

yi代表预测值，在本文中指猪肉价格预测值，w代表超平面的法向量，x代表样本点向量，即本文选取的影响猪肉价格的特征指标构成的向量，b代表可调因子，通过计算可得出方程最优系数w和b。

对于超平面方程的求解，其原理是一个约束的非线性规划问题（崔建明等，2013）：

这是一个严格的凸规划，目标函数和二次约束函数均是凸函数。范数最小的满足约束的w就是最优分类超平面的法向量。根据最优化理论和凸二次规划方法，可以把它变成沃尔夫的双重问题来解决：

只需将对偶问题中的点积用卷积函数K(xi,xj)代替。

最后的模型表示为：

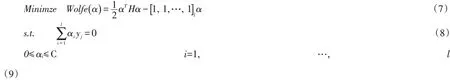
式中，H是一个半正定的对称阵Y=1（线性的情况为

对于Kuhn-Tucker条件，这个对偶问题仍是一个有约束的二次规划，也可等价地表示为：

作为奇卡娜文学代表作家，西斯内罗斯在作品中探讨墨西哥裔女性面临的三重的压迫:作为少数族裔，她们在白人社会中处于边缘地位，不被主流社会所接纳；作为女性，她们受到墨西哥传统价值观念的束缚和压制，在男性主导的家庭生活中处于“他者”地位；此外，她们不被同性，特别是墨西哥传统女性所理解，从而陷入孤独的境地。西斯内罗斯笔下的女性多以几代的群像出现，集中表现为墨西哥传统女性，第一代墨西哥裔女性移民和第二代墨西哥裔女性移民。她们之间的冲突既是代际冲突，又是文化和价值观念的冲突。

式中，μi就是分类平面函数作用在xi上的输出：

五、猪肉价格预测与风险预警结果分析

根据综合选取法，将最终确定的7个特征指标输入模型，通过SVM中常用的SVR算法和径向基（RBF）核函数，利用交叉验证法选择最佳参数。本文所需数据为时间序列数据，由于选取的特征指标至少滞后一期，故用于实际操作的数据样本起止时间为2009年3月～2021年11月，共153个样本。其中，2009年3月～2021年4月的数据（即前146个样本）作为SVM模型的训练样本，根据训练样本建立SVM模型进行模型的训练和拟合。2021年5月～2021年11月的数据（即后7个样本）作为预测样本，用于对模型进行验证。本文运用台湾大学林智仁开发的Libsvm软件包来建立基于SVM的猪肉价格预测模型，模型操作借助Matlab R2017b软件处理。

（一）数据归一化处理

为了避免在建模时因为数据间数量级差别较大或量纲不同对模型的预测准确性产生影响，保证输出数据中数值较小的数据不会被吞食，提高收敛速度，缩短训练的时间，故在建模之前对选取的数据进行归一化处理，将数据统一到[-1，1]的区间内。

（二）支持向量机模型的参数选择

选择上述7个指标建立SVM模型进行猪肉价格的预测，在预测之前首先需要确定SVM模型的参数，C、g、p是SVM算法的主要参数。其中，C为惩罚参数，g为RBF核函数的宽度系数，这是建立SVM模型中重要的两个参数，主要影响模型的学习能力和泛化能力。在参数调整过程中，始终固定p为默认值0.01，同时利用交叉验证法确定C和g的值。

先固定g为默认值，即g=0.1，再通过调整C值模拟预测结果，调整过程如表5所示。从表中可以看出，随着C值变化，均方误差和平方相关系数也在变化。当C值小于21时，均方误差逐渐变小，当C值大于21时，均方误差逐渐变大，平方相关系数在C值等于21时最大，为0.834，因此，C值选择均方误差最小和平方相关系数最大时的值，即C=21。

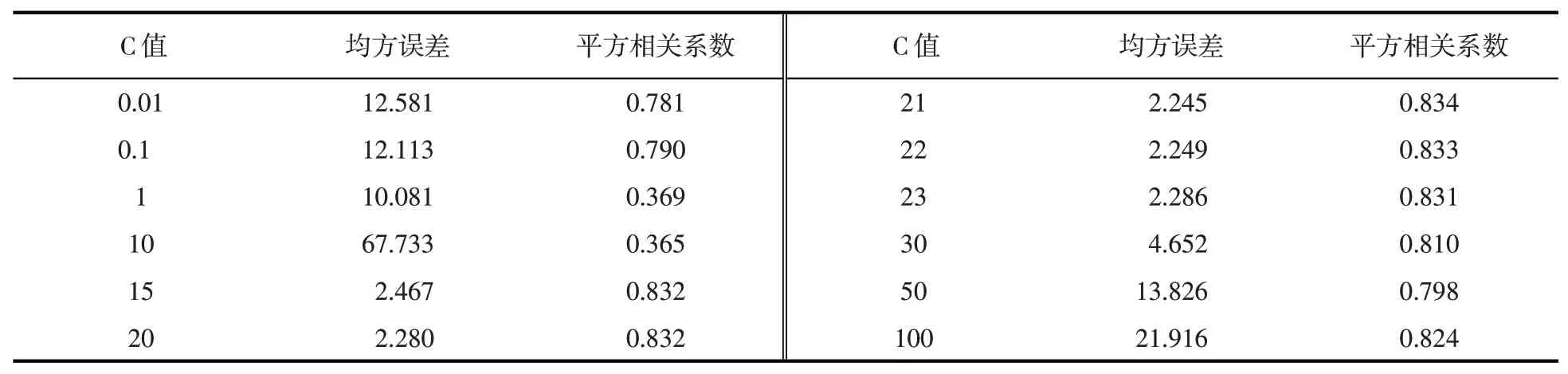
表5 不同C值下的模型拟合精度

固定C=21，p=0.01，由表6可知，随着g值变化，均方误差和平方相关系数也随之变化。当g值小于0.31时，均方误差在不断波动变化，g为0.01时均方误差较大，后又逐渐变小。当g值大于0.31时，均方误差逐渐变大，平方相关系数在g=0.31为0.919。当g等于0.3时，平方相关系数为0.921，大于0.919，但因均方误差对模型拟合优度的影响更大，综合考虑，g值选择均方误差最小时的值，即0.31。综上分析，寻优后得到的惩罚因子C和核函数参数g最优组合为（21，0.31），均方误差最小为1.032，平方相关系数最高为0.919。

表6 不同g值下的模型拟合精度

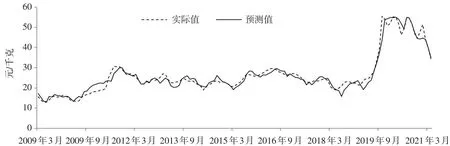
图1 SVM训练样本的真实值与预测值对比

进一步将预测样本代入已建立的SVM模型进行预测分析，2021年5月～2021年11月猪肉价格的预测结果如表7所示。从表中猪肉价格实际值与预测值可知，猪肉价格自2021年5月起，一直呈下降趋势。主要原因是2018年非洲猪瘟爆发期间大量生猪死亡造成猪肉供给量紧缺，在经历短期恐慌后，猪肉消费需求基本恢复，供小于求造成猪肉价格暴涨，直至2021年上半年猪肉价格始终处于高位运行水平。在猪肉价格上涨期间，趋利动机促使现有养殖者扩大养殖规模，同时新的养殖者也不断加入，使后期生猪产能呈现持续恢复态势，进而导致后疫情时期猪肉供给大幅增加，猪肉价格下跌。

表7 猪肉价格预测结果

由预测结果可知，猪肉价格预测值和实际值相近，SVM模型预测值的输出结果基本拟合了实际值的变化趋势，两者具有较高的一致性。仅2021年7月的预测值与实际值稍有差异，但预测值整体趋势与实际趋势基本保持一致，说明本文预测模型构建较为合理，可以为猪肉价格波动的预期值提供一定的参考。本文特征指标的滞后期选择至少为一期，因此可以滚动预测未来一个月的猪肉价格变化情况，即可预测2021年11月猪肉价格为21.867元/千克。猪肉价格预测值可为市场参与者提供决策参考，特别是避免生猪疫情爆发期间养殖者的盲目决策对猪肉市场造成的进一步冲击，促进市场供应的基本稳定。

（三）猪肉价格风险预警分析

在进行猪肉价格风险预警时，警情指猪肉市场上供求不平衡，外在表现为价格风险，即猪肉价格上下大幅波动。通常警情指标都以波动率来衡量，波动率也可以度量猪肉价格波动的实际情况，故本文以猪肉价格波动率作为猪肉价格风险预警的警情指标。采用2009年2月～2021年10月猪肉价格实际值的月度数据建立猪肉价格风险预警的警限与警度，计算得出研究区间内的猪肉价格波动率。猪肉价格波动率的月平均值为0.38%，标准差为7.169%。根据猪肉价格的历史波动率确定警限，划分具体的警度区间。在没有生猪疫情冲击时，猪肉价格波动保持在一定范围内，生猪疫情发生造成猪肉价格出现大幅波动则属于异常现象，最终表现为不同程度的警情，应引起相关部门的关注，以及时采取措施缓解价格的过度变动。

基于猪肉价格的历史波动率，同时考虑猪肉价格波动率的变化趋势，划分具体的预警区间。表8中波动警限的设置是依据3σ原则设定的。首先，依据猪肉价格的实际值计算实际的猪肉价格波动率①实际的猪肉价格波动率=本期猪肉价格实际值-上期猪肉价格实际值/上期猪肉价格实际值，同理计算得到预测的猪肉价格波动率②预测的猪肉价格波动率=本期猪肉价格预测值-上期猪肉价格实际值/上期猪肉价格实际值。进一步参考表8猪肉价格波动警限划分标准，并根据猪肉价格波动率确定预警警度，结果如表9所示。由表9可知，预测的猪肉价格波动率与实际的猪肉价格波动率变化趋势基本一致，仅2021年7月两者相差较大，预测警度与实际警度存在一定偏离。从表中6个月的猪肉价格数据来看，实际警度和预测警度普遍处于重度偏低或偏低水平，表明猪肉价格下降幅度大，猪肉市场处于供给过剩状态。

表8 猪肉价格波动警限的设定

由表9可知，预测的猪肉价格波动率整体呈负向波动状态，但波动率逐渐呈缩小趋势，说明在生猪疫情恢复期，猪肉供给明显增加，市场处于供过于求状态。其中2021年9月和10月猪肉价格下降明显，降低至20元/千克以下，且2021年10月猪肉价格波动警度区间为正常状态，主要原因可能是时值开学季和国庆节，虽然猪肉供给已有明显增加，但节假日期间居民猪肉需求增幅更大，使供大于求状态逐渐向供求平衡状态转变，实际警度与预测警度由偏低转为正常。2021年11月猪肉价格预测值上升，猪肉价格较上期波动率变大，预测警度为重度偏高水平，市场参与者可据此提前采取措施以避免猪肉价格进一步剧烈波动。

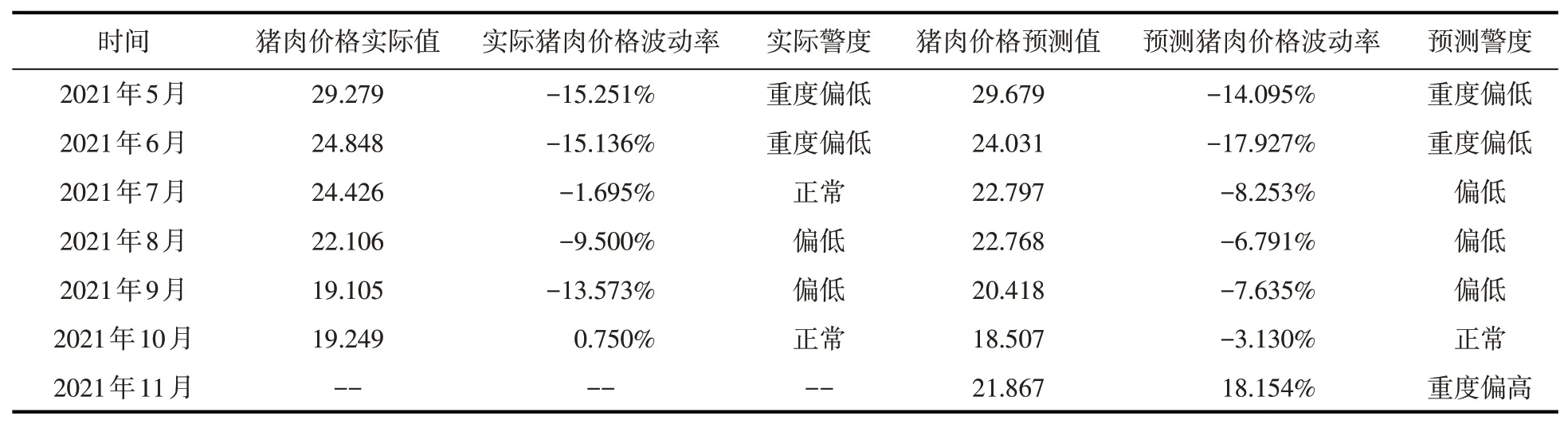
表9 猪肉价格波动警度预测结果

六、结论与政策建议

（一）结论

研究表明，选取滞后6期的月度生猪存栏、滞后1期的猪肉进口、滞后1期的生猪养殖利润、滞后1期的豆粕价格、滞后6期的宏观经济景气一致指数、滞后6期的RPI建立SVM模型预测猪肉价格具有较好的预测效果，确定SVM的最优参数后，均方误差最小为1.032，平方相关系数最高为0.919，模型的预测精度较高。猪肉价格风险预警结果显示，自2021年5月以来，猪肉价格呈大幅下跌趋势，实际警度与预测警度整体表现为重度偏低及偏低水平，猪肉市场处于供给过剩状态。

（二）政策建议

1.完善猪肉价格预测信息系统，增强价格预测时效性

价格预测系统包括基础数据的采集、管理、处理。猪肉价格影响因素较多，参照本文研究结论，对于生猪存栏、仔猪肉进口、生猪养殖利润等关键影响因素的指标数据，应加强采集、处理、公布的时效性。建立猪肉价格预测信息系统，优化价格预测方法，基于特征指标实时、科学预测猪肉价格，并根据历史数据识别判断猪肉价格风险，为市场相关主体提供有效的决策标准，使其在重大疫情发生的背景下及时合理采取措施控制价格过度波动，保障市场机制有序运行。

2.畅通猪肉价格信息发布渠道，促进信息实时共享

信息不对称是市场风险的重要原因之一，市场信息管理部门应及时发布猪肉价格预测信息及相关产品价格信息，同时简化相关信息查询方式，促进信息共享。这有利于市场主体及时、准确掌握市场发展趋势，避免信息不对称导致的市场失灵现象，引导市场生产经营者依据预测信息自主调节生产经营决策，主动适应市场形势变化，也有助于促进消费者合理决策、理性消费。

3.健全猪肉价格风险预警体系，提高应急调控水平

不断强化重大不确定性事件爆发后的应急调控机制，保证市场供应及价格稳定。非洲猪瘟等突发性生猪疫情具有不可预测性，其影响也更为严重。一方面，政府相关部门应根据猪肉价格波动警度信息合理指导、协调中央储备冷冻肉的投放和收储工作，保证猪肉供应处于相对稳定水平。另一方面，畜牧管理部门应借助猪肉价格预测信息正确引导市场参与者决策行为，指导养殖者的生产活动和消费者的消费行为，减轻生猪疫情带来的负面影响。