Triaxial test on glass beads simulating coarse-grained soil
2023-01-02WenDongXuXueFengLiWenWeiYangHongJinJia
WenDong Xu,XueFeng Li,WenWei Yang,HongJin Jia
1.School of Civil and Hydraulic Engineering,Ningxia University,Yinchuan,Ningxia 750021,China
2.Solid Mechanics Institute,Ningxia University,Yinchuan,Ningxia 750021,China
3.Ningxia Center for Research on Earthquake Protection and Disaster Mitigation in Civil Engineering,Yinchuan,Ningxia 750021,China
4.School of Physics and Electronic-Electrical Engineering,Ningxia University,Yinchuan,Ningxia 750021,China
ABSTRACT It is feasible to study the mechanical characteristics of coarse-grained soil by simulated granular materials such as glass beads.In this paper,3 mm diameter glass beads are used to conduct drained and undrained triaxial tests under the condition of different confining pressures to explore their strength,deformation and critical state characteristics.Specifically,the influence of drainage and confining pressure on the stick-slip phenomenon of glass beads is reported.The experimental findings from triaxial tests show that the stress-strain relationship of glass beads softens when the confining pressure is high.Under the undrained condition,the initial modulus increases with the increase in the confining pressure.In contrast,it is not significantly affected by the confining pressure under the drained condition.It is quite evident that the glass beads hardly contract during the shearing process,and their stress path is approximately a segmented straight line.The slope of the critical state line under the undrained condition is greater than that under the drained condition,and the friction angle of the glass beads under the undrained and drained conditions is calculated to be 28.1° and 29.5°,respectively.The phenomenon of stick-slip has been depicted for the different test conditions,and the stick-slip amplitude linearly increases with the confining pressure,especially in the undrained condition.It is also found that the maximum energy released from the phenomenon of stick-slip increases linearly with the confining pressure.
Keywords:triaxial test;glass beads;strength;critical state;stick-slip
1 Introduction
Coarse-grained soil,such as sand and gravel,is a granular material composed of a large number of discrete particles.Because of the discreteness,the macromechanical behavior of granular materials is very complex,depending on the micro-mechanical behavior of each particle.When the material is affected by the external force or the internal stress state is changed,the movement state of the whole particle will change correspondingly.The microscopic contact between the particles controls the macroscopic movement state of the entire system.Therefore,the basic properties of particles,such as particle size,shape and inter-particle contact force,play a vital role in the macroscopic mechanical behavior of granular materials(Zhouet al.,2016;Jiang,2019).Understanding the influence of these factors on the overall mechanical behavior,especially the shear behavior,is very important in the application of granular materials,as it may cause serious engineering problems,such as road collapse,landslides,etc.(Tanget al.,2016).
Ideal spherical particles are usually selected as models to study the general behavior of granular materials.In investigating the deformation characteristic of coarse-grained soil,Chenget al.(2007)chose glass beads to conduct triaxial tests and concluded that the yield of the spherical particle aggregate is overall structural yield,and the deformation is the irreversible plastic deformation caused by the adjustment of the particle position.Konget al.(2010)used steel beads to simulate the triaxial test of rockfill materials,discussed the microscopic deformation mechanism,and modified the Rowe dilatancy equation to better adaptability to non-slip particle deformation.As ideal spherical particles,glass beads are isotropic material.However,when the glass beads are subjected to isotropic pressure,it is found thatεx=εy=2.2εz,whereεzis the strain in the vertical direction,andεv=5.4εz,that is,isotropic materials still have anisotropy in different directions in the triaxial test(Haruyama,1981).In addition,the glass beads can be used to study the crushing properties of granular materials because they are not affected by the anisotropy of the materials(Takeiet al.,2001).It is worth mentioning that glass beads or steel beads can be used as the basic particles for indoor experiments,making it possible to compare Discrete Element Model(DEM)simulations with test results(Hassanpouret al.,2004).Wuet al.(2017a,2017b,2017c)performed a series of triaxial tests and numerical simulation triaxial tests on the glass beads and compared the test results with the numerical simulation results.They found that the numerical model can simulate the deviatoric curves well as long as the test sample remains cylindrical.At the same time,triaxial tests and DEM also can be used to verify constitutive models(Dondiet al.,2012).
Stick-slip is a common phenomenon of granular materials.This mechanism,when occurring in rocks,is considered to be the source of earthquakes(Brace and Byerlee,1966).In addition,it is found that the shear process under drying conditions will produce an obvious stick-slip phenomenon in the study of the mechanical behavior of coarse-grained soil(Cavarrettaet al.,2010).This phenomenon is usually attributed to the formation and collapse of the force chain,which is related to the confining pressure,particle size,smoothness,loading rate and other factors(Adjemian and Evesque,2004;Doanhet al.,2013;Cuiet al.,2017).In this regard,Ozbayet al.(2016)found that the amplitude of deviator stress and axial displacement increased with the increase of confining pressure.And with the rise in strain rate,the amplitude of deviator stress decreases.Alshibliet al.(2006)studied glass beads of different sizes,and the results showed that the stick-slip phenomenon could be observed except for glass beads with a diameter of 3.3-3.6 mm.The study also found that the stick-slip amplitude has a linear relationship with the confining pressure.However,in the study of Wuet al.(2017a),the stick-slip phenomenon of 4 mm glass beads can be clearly observed.Moreover,the studies on the stick-slip phenomenon in the existing literature are all under drained conditions;undrained behavior is rarely discussed.
Critical state theory is the foundation of many constitutive models used in computer simulation of soils.Therefore,it is of scientific and engineering significance to investigate the critical state characteristics of spherical granular materials(Liet al.,2014).However,few references can be found on this front.In addition,glass beads are spherical particles and have a relatively smooth surface,which can directly affect their strength and deformation characteristics.
Because of the complex nature of coarse-grained soil,such as irregular particle shape and weathering degree,variation in joint micro-cracks and mineral composition,etc.,many factors which influence the mechanical properties of materials are coupled together,and it is difficult to study the influence of a single factor.To quantitatively explore the influence of a single factor on the mechanical behavior of coarsegrained soil,an ideal granular material,i.e.,glass bead,was selected.In this paper,3 mm glass beads are used to conduct drained and undrained triaxial tests under different confining pressures to explore their strength,deformation and critical state characteristics.And the stick-slip phenomenon of glass beads is observed and analyzed.
2 Materials and methods
2.1 Glass beads
The test uses glass beads with a diameter of 3 mm made in Germany,as shown in Figure 1.The main component of the glass beads is silica,and its basic parameters are listed in Table 1.Compared with coarse-grained soil,glass beads are approximately isotropic granular materials with smoother surfaces.
2.2 Triaxial device
Figure 2 is the triaxial device use d in this test.The triaxial device includes:
—Axial servo motor(noted a),with a maximum axial force of 30 kN and the load applied by lifting the bottom-plate(noted e);
—A triaxial cell(noted b)used to place the sample and load it;
—An axial force transducer with a maximum load of 10 kN(noted c)and a measurement accuracy of±1%FS(full scale);

Figure 1 View of glass beads

Table1 Basic parameters of glass beads

Figure 2 Triaxial test devices
—An axial displacement transducer(noted d),with its upper end fixed and its lower end in contact with the triaxial cell(noted b);
—A pore water pressure transducer(noted f)used to measure the pore water pressure inside the sample;
—Back-pressure controller(noted g)to apply back pressure to the sample by injecting or releasing airless water with a maximum back-pressure of 0.99 MPa;
—Confining pressure controller(noted h)to apply confining pressure to the triaxial cell(noted b)by injecting or releasing airless water,with a maximum pressure of 1.99 MPa;
—An airless water container(noted i)connected to the base of the triaxial cell,with airless water injected into the sample through the difference of hydrostatic head;
—A thermometer(noted j)to monitor the temperature and humidity in the laboratory;
—A computer(noted k)with the SLB software to control the test conditions and collect test data.
2.3 Samples preparation
Cylindrical experimental samples of 61.8 mm diameter and 125.0 mm height were prepared with a relative density of 68.4% and a void ratio of 0.52.They are prepared in five layers with the undercompaction method to keep the density of the sample consistent within the height range(Ladd,1978).This method suggests that the relative density of the upper and lower soil samples differ by 1%.The specific steps are as follows:
(1)A total of 607 g glass beads was weighed and divided into five parts according to the weight from light to heavy:117.8 g,119.6 g,121.4 g,123.2 g,125 g.
(2)A latex membrane is mounted on the base of the triaxial cell,and a porous stone and filter paper are placed in turn.
(3)The membrane-bearing cylinder is installed on the base of the triaxial cell.A vacuum pump applies 15 kPa negative pressure to ensure the latex membrane is in close contact with the inner wall of the cylinder.
(4)Pour the divided glass beads into the latex membrane slowly and uniformly in sequence.
(5)A rubber mallet is used to evenly and symmetrically tap the outer wall of the cylinder,and the height of the sample is controlled to be 125±1 mm.
(6)Filter paper,porous stone and loading cap are gently placed on the sample in sequence.And the latex membrane is tied to the loading cap.
2.4 Test procedure
Triaxial drained and undrained tests under five different confining pressures are performed on the specimens.The specimens are loaded at a rate of 0.12 mm/min until the axial strain reaches 25%.The five initial confining pressures,σ3,are 50 kPa,100 kPa,150 kPa,200 kPa,and 250 kPa.The test process is introduced as follows:
—Saturation step:Saturation is divided into hydrostatic-head saturation and back-pressure saturation.First,a hydrostatic head saturation is conducted.Here,airless water is added to the sample through a container and flows out through a drain pipe.The end condition of hydrostatic head saturation is that the volume of water discharged from the sample is more than three times the sample volume.In the following back-pressure saturation,back pressure and confining pressure are applied in increments of 50 kPa to help the residual gas inside the sample dissolve in water,while the confining pressure is maintained at 20 kPa higher than the back pressure.When the confining pressure reaches about 200 kPa,the SkemptonB-value is assessed.IfB-value is less than 0.95,the sample is not saturated.The confining pressure and back pressure continue to increase untilB-value>0.95,when the sample is considered to reach the required saturation.
—Isotropic consolidation step:Apply different effective initial confining pressuresσ3to the sample.The end condition is that the volume of water discharged from the sample is less than 1% of the sample volume within 30 minutes.
—Constant strain rate shearing step:The axial load is applied to the specimen at a constant rate of 0.12 mm/min until the axial strain reaches 25% while the confining pressure is kept constant.
3 Results and discussions
3.1 Stress-strain characteristics
Figure 3 shows the stress-strain relationship of glass beads under undrained conditions.It can be seen from Figure 3 that the stress-strain relationship of glass beads exhibits strain-softening behavior,especially under high confining pressure.One can observe that the initial modulus increases with the confining pressure.The main reason is that the larger the confining pressure before shearing,the greater the relative density of the material,and the stronger the occlusion ability between particles and the ability to resist shearing deformation.Figure 4 shows the stress-strain relationship of glass beads under drained conditions.Compared with Figure 3,it can be seen that the peak strength is lower than that under undrained conditions.The influence of confining pressure on its initial modulus is not obvious under drained conditions,and glass beads are approximately rigid-perfectly plastic materials.
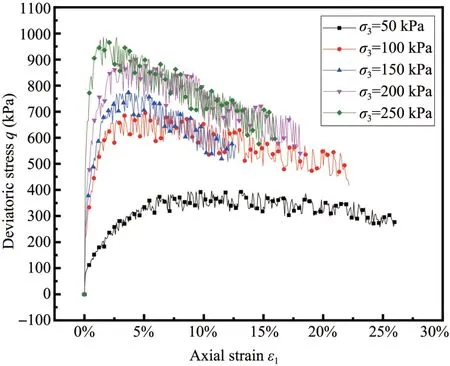
Figure 3 Stress-strain relationship of glass beads under undrained conditions

Figure 4 Stress-strain relationship of glass beads under drained conditions
3.2 Deformation characteristics
Figure 5 shows the relationship between volumetric strain and axial strain under drained conditions.As can be seen from Figure 5,the glass beads hardly contraction and the volumetric strain is dilation during the shearing process.This phenomenon can be explained from the macroscopic perspective,since glass beads are cohesionless materials and have a smooth surface,and the glass beads are in the dense state initially and are difficult to contract."Crackling"sound of glass beads can be heard from inside the sample during the test,indicating that the position of the particles is adjusted sharply and the volume of the sample changes suddenly.

Figure 5 Relationship between volumetric strain and axial strain
Figure 6 shows the deformation of the glass beads sample under drained conditions when the axial strain is 25%.Obvious shear bands can be observed in the sample.The inclination angles of the shear bands at confining pressure of 200 kPa and 250 kPa are approximately 40.5° and 37.8°,respectively,which are less than 45° and do not conform with the Coulomb criterion as shown in Equation(1):

whereθis the inclination angles of the shear bands andφis the internal friction angle.In those cases of undrained loading,the deformation of the glass beads sample is shown in Figure 7,and the same observation can be observed in terms of the inclination angle.

Figure 6 Shear deformation of glass beads under drained conditions at the axial strain of 25%

Figure 7 Shear deformation of glass beads under undrained conditions at the axial strain of 25%
3.3 Critical state
Figure 8 shows the effective stress path of glass beads under undrained conditions.The stress path rises from the initial stress point to the peak strength line and moves upward along the peak strength line.After reaching the peak strength,it drops and converges to the critical state line.Figure 9 shows the effective stress path of glass beads under drained conditions.One can observe that the effective stress path under drained conditions rises to the peak strength line along a straight line with a slope of 3 to 1 and then gradually returns to the critical state line.
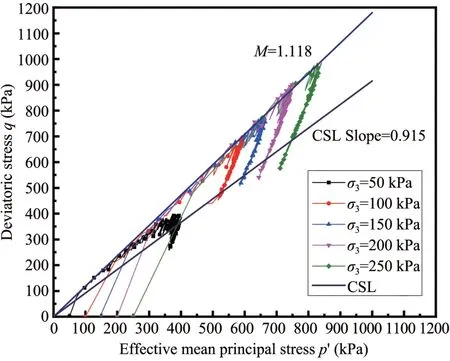
Figure 8 Effective stress path of glass beads under undrained conditions

Figure 9 Shear deformation of glass beads under drained conditions
In thep'-qplane,q=Mp'whereMis the effective stress ratio.Through its stress path curve,the effective internal friction angleφof the glass beads can be found to be 28.1° under undrained conditions and 29.5° under drained conditions by using the following Equation:
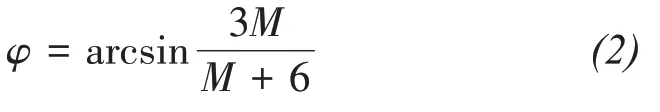
3.4 Stick-slip phenomenon
The stick-slip phenomenon under drained and undrained conditions can be observed in Figure 3 and Figure 4.The stick-slip phenomenon at 250 kPa is more obvious than lower confining pressure.Figure 10 replots the stress-strain relationship of glass beads at 250 kPa under undrained conditions to examine the stick-slip phenomenon in detail.The first stick-slip(Sfirst)instability occurs at a small strain,about 0.71%,and the axial displacement is about a third of the diameter of the glass bead.The maximum deviator stress(qmax)is 975.6 kPa,the minimum deviator stress(qmin)is 576.2 kPa,and the maximum stick-slip amplitude(Δqmax)is 163.2 kPa.
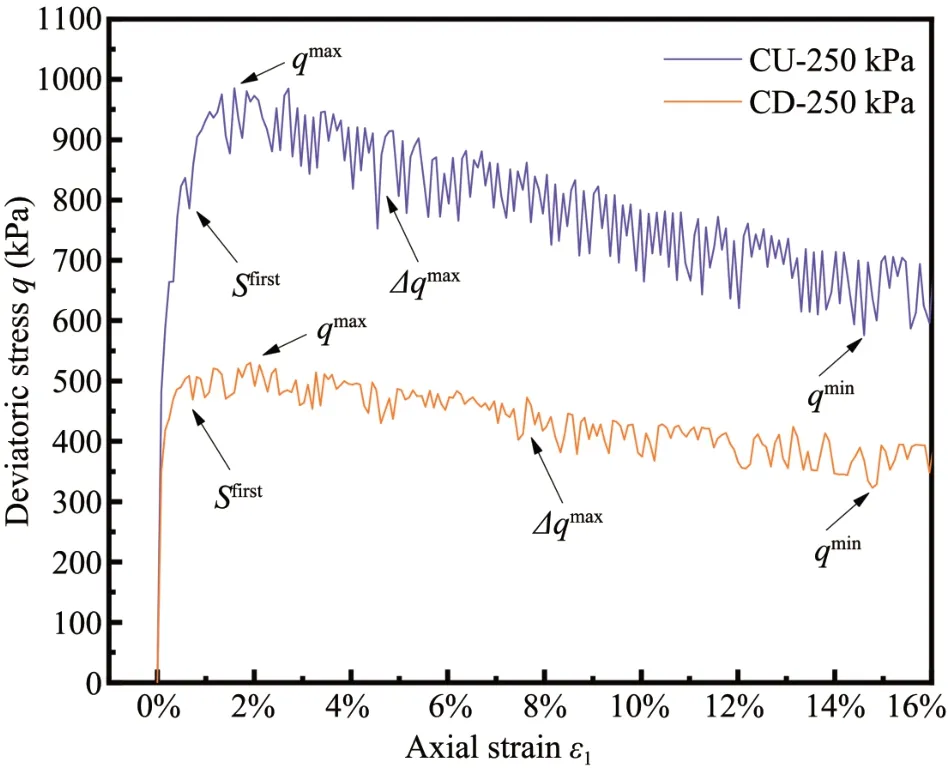
Figure 10 Stress-strain under 250 kPa confining pressures under undrained and drained conditions
The first stick-slip(Sfirst)instability is also observed to be closely related to confining stress.As illustrated in Figure 11,the axial strain corresponding to the first stick-slip instability increases with confining pressure,and the end of the curve tends to plateau.Under higher confining stress,the structure of glass beads is more stable and the first stick-slip phenomenon appears at larger axial strain.
Figure 12 depicts the variation in the maximum deviator stress(qmax)with the confining pressure under drained conditions.qmaxincreases with confining pressure,and a linear fit can be identified with a high correlation coefficient of 0.971.However,under undrained conditions the relationship ofqmaxwith confining pressure is not obvious.

Figure 11 Axial strain at first slip versus confining stress under undrained and drained conditions
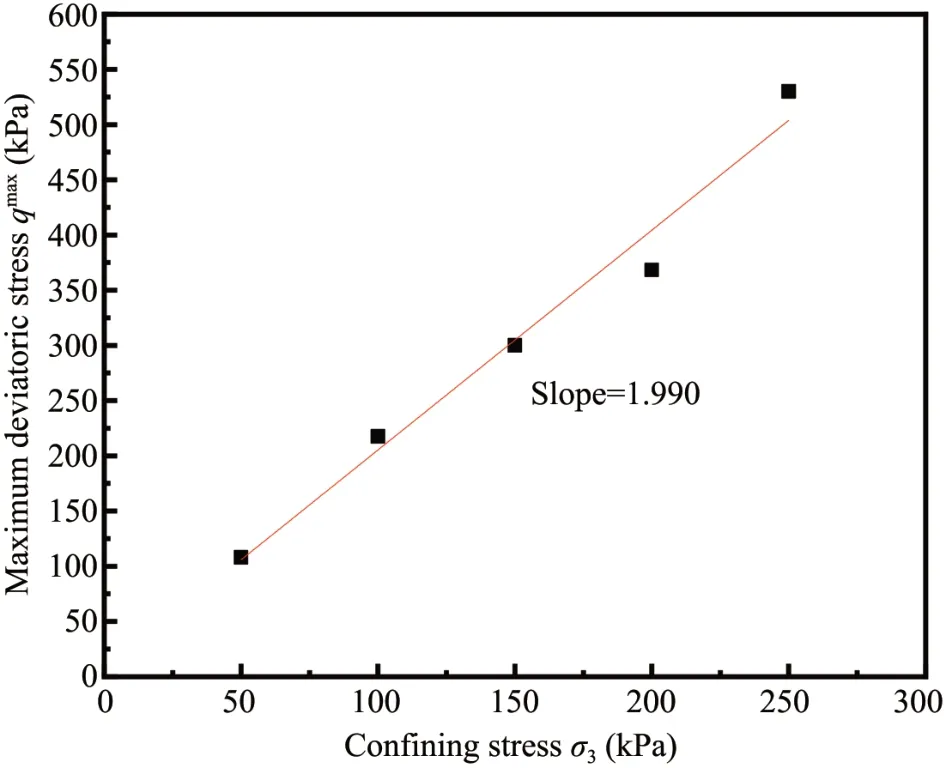
Figure 12 Maximum deviatoric stress versus confining stress under drained conditions
Figure 13 shows the relationship between the maximum deviatoric stress drop during stick-slip(Δqmax)and the confining pressure.It can be seen from Figure 13 thatΔqmaxrises approximately linearly with confining pressure at slopes of 0.272 and 0.577 under drained and undrained conditions,respectively.It is worth noting that under drained conditions,the stickslip phenomenon is relatively weaker than that under undrained conditions.
Once the slip phenomenon occurs,the deviator stress in the sample will suddenly decrease,which depends on the energy accumulation of the system.Figure 14 shows the effect of confining pressure on the maximum slip rate.In this figure,the slip rate is expressed as a ratio of the amplitude of stress drop(kPa)to the slip time(s).It can be seen that the maximum slip rate increases linearly with the increase in confining pressure.Under undrained conditions,the maximum slip rate is greater than that under drained conditions.According to the variation of deviator stress and displacement,the maximum energy released during stick-slip,defined as the slip force(N)times slip distance(m),can be evaluated and its variation with confining pressure is illustrated in Figure 15.The energy is released through the collision between the glass beads and the evident acoustic emission during the test.
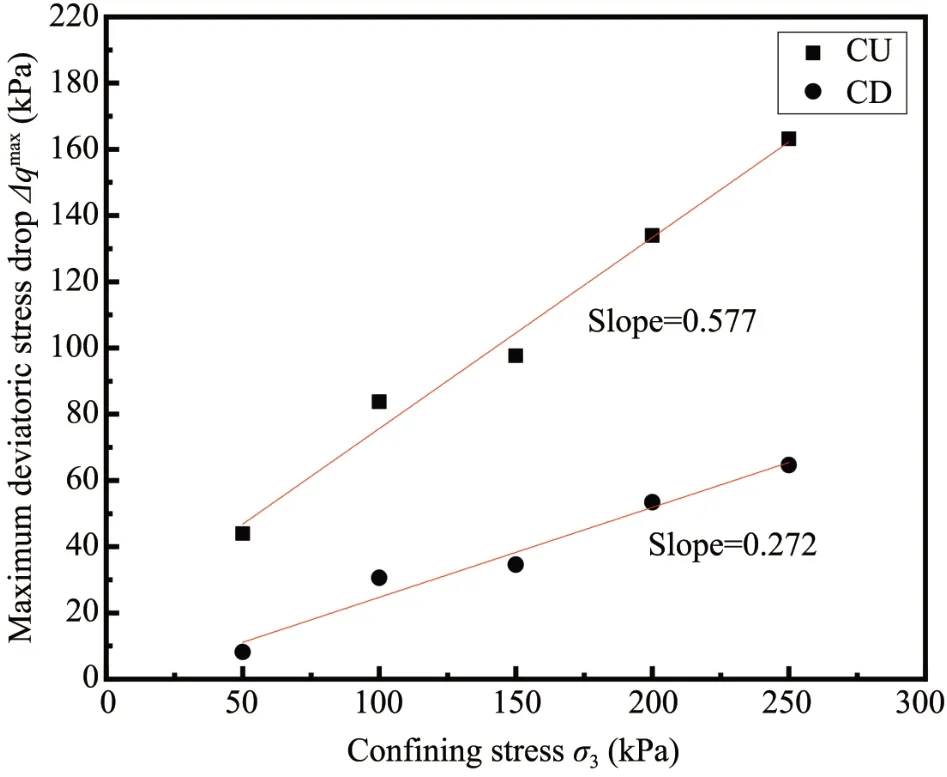
Figure 13 Maximum deviatoric stress drop versus confining stress
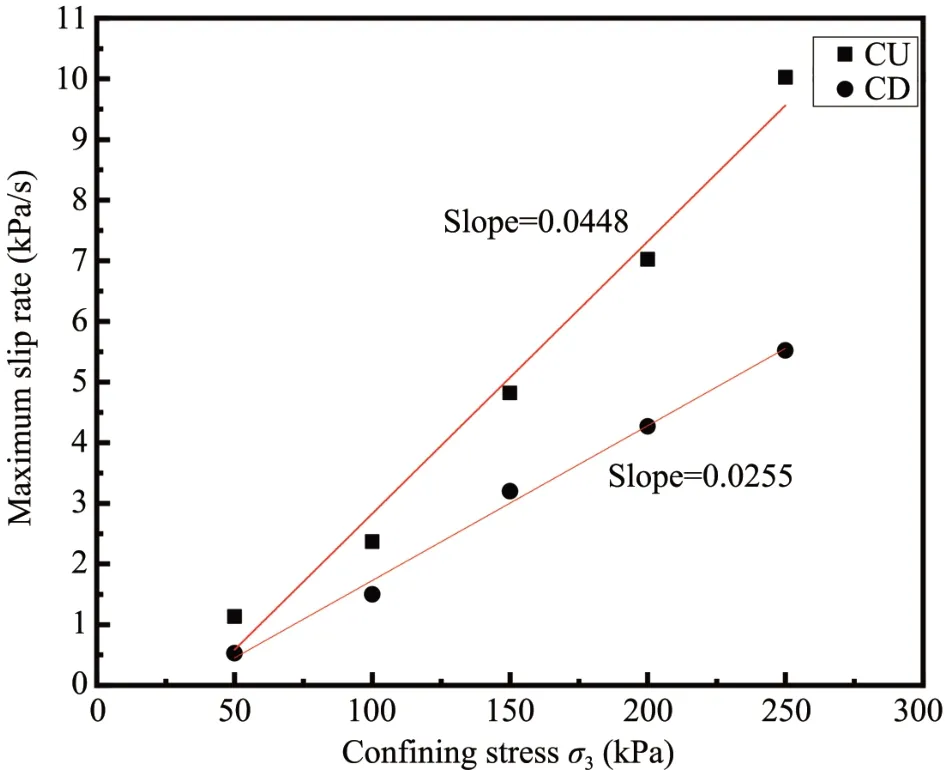
Figure 14 Maximum slip rate of stress versus confining stress
4 Conclusions
This paper describes and analyzes the results of drained and undrained triaxial tests performed on 3 mm diameter glass beads.The following conclusions are obtained:
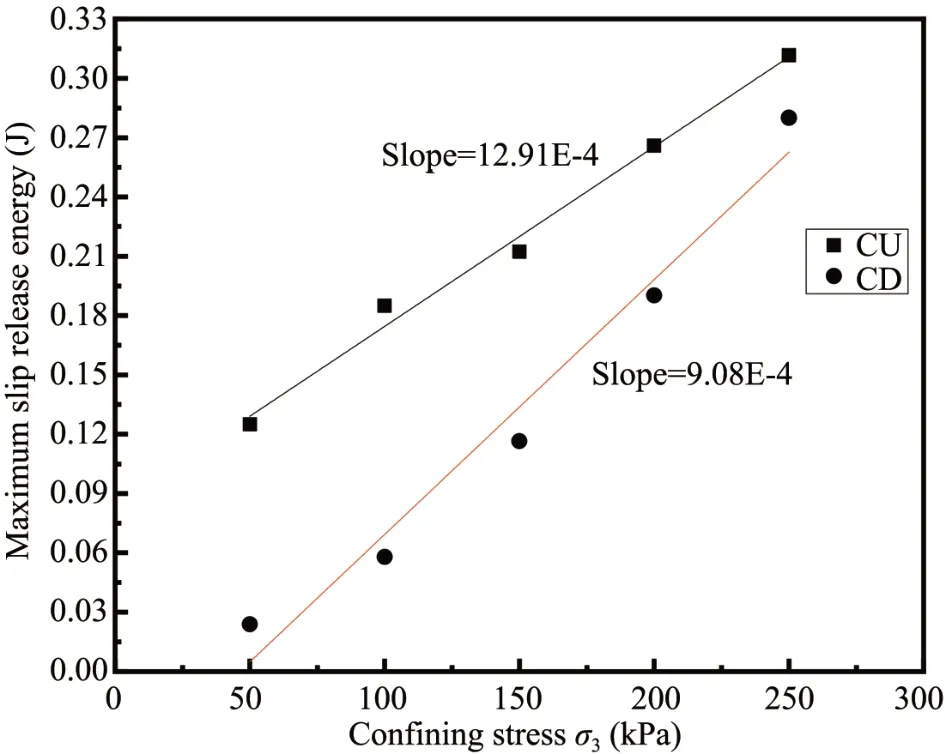
Figure 15 Maximum slip release of energy versus confining stress
(1)The stress-strain relationship of glass beads under high confining pressure is strain-softening.Under undrained conditions,the initial modulus increases with the increase in the confining pressure.In contrast,under drained conditions,the initial modulus is not significantly affected by the confining pressure.
(2)The glass beads hardly contract during the shearing process.The inclination angle of the shear bands does not conform to the Coulomb criterion.
(3)The slope of the critical state line under undrained conditions is steeper than that under drained conditions,and the friction angle of the glass beads under undrained and drained conditions is found to be 28.1°and 29.5°,respectively.
(4)The phenomenon of stick-slip is examined for different conditions.The findings reveal that the stickslip phenomenon is more obvious under undrained conditions,and its amplitude linearly increases with the confining pressure.It is also found that the maximum energy released from the stick-slip increases linearly with the confining pressure.
Acknowledgments:
This work was financially supported by the National Natural Science Foundation of China(No.1216020092),and the Projects for Leading Talents of Science and Technology Innovation of Ningxia(No.KJT2019001),and the innovation team for multiscale mechanics and its engineering applications of Ningxia Hui Autonomous Region,and these supports are gratefully acknowledged.
杂志排行
Sciences in Cold and Arid Regions的其它文章
- The influence of the underpassing frozen connecting passage on the deformation of the existing tunnel
- Influence of freeze tube deviation on the development of frozen wall during long cross-passage construction
- Thermal-Hydro-Mechanical coupled analysis of unsaturated frost susceptible soils
- Frozen curtain characteristics during excavation of submerged shallow tunnel using Freeze-Sealing Pipe-Roof method
- Discussion on pile axial load test methods and their applicability in cold regions
- Application of automated cone penetrometer for railway investigation using correlations with DCPI and Deflection Modulus
