Thermal-Hydro-Mechanical coupled analysis of unsaturated frost susceptible soils

YuWei Wu,Tatsuya Ishikawa

1.Graduate School of Engineering,Hokkaido University,Hokkaido 060-8628,Japan

2.Faculty of Engineering,Hokkaido University,Hokkaido 060-8628,Japan

ABSTRACT Damage caused by frost heave leads to costly maintenance in cold regions,like Hokkaido,Japan.Therefore,the study of the frost mechanism with experimental and numerical methods has been of great interest.Numerous models have been developed to describe the freezing process of saturated soil,which differs from the partially saturated conditions in the field.In fact,most subsurface soils are unsaturated.The freezing process of partially saturated soils is more complex than saturated soils,as the governing equations show strongly nonlinear characteristics.This study proposes a thermo-hydro-mechanical coupled model considering the heat transfer,water infiltration,and deformation of partially saturated soil to reproduce the freezing process of partially saturated frost susceptible soils distributed in Hokkaido.This model better considers the water-ice phase change and soil freezing characteristic curve(SFCC)during freezing under field conditions.The results from the multiphysics simulations agree well with the frost heave and water migration data from frost heave tests of Touryo soil and Fujinomori soil.In addition,this study discussed the influence of the various factors on frost heave amount,including temperature gradients,overburden pressures,water supply conditions,cooling rates,and initial saturation.The simulation results indicate that the frost heave ratio is proportional to the initial degree of saturation and is inversely proportional to the cooling rate and overburden pressure.

Moreover,simulation under the open system generates much more frost heave than under the closed system.Finally,the main features of the proposed model are revealed by simulating a closed-system frost heave test.The simulation results indicate that the proposed model adequately captures the coupling characteristics of water and ice redistribution,temperature development,hydraulic conductivity,and suction in the freezing process.Together with the decreased hydraulic conductivity,the increased suction controls the water flow in the freezing zone.The inflow water driven by cryogenic suction gradient feeds the ice formation,leads to a rapid increase in total water content,expanding the voids that exceed the initial porosity and contributing to the frost heave.

Keywords:frost heave;unsaturated soil;Thermal-Hydro-Mechanical(THM)coupled model;Finite Element Method(FEM).

1 Introduction

Hokkaido is a cold and snowy island in northern Japan that experiences frost heave damage in the cold season.Frost action is generally developed in frostsusceptible soils,where the increase in suction induced by ice formation at the freezing front causes moisture migration from the unfrozen area to the freezing front.As a result,ice accumulates and forms ice lenses at the freezing front.The ice lens formation and surface heave in seasonally freezing areas like Hokkaido pose an adverse impact on engineering and agriculture applications(Konrad,2005;Zhaoet al.,2013),including cracking of pavements,damage to the pile foundations,and fracture of pipelines.Thus,it is necessary to understand the mechanisms of soil freezing.The fundamental behaviors of the frost susceptible soils under frost action have been investigated through experimental,analytical,and numerical approaches.As frost action is a complex moisture-heatmechanics interaction process,laboratory-controlled experiments to illustrate frost heave mechanisms in frost susceptible soils are restricted by the difficulties in measuring parameters like permeability and relative hydraulic conductivity.These parameters apparently influence the cryogenic suction and the depression of the freezing point,which are important in the frost action.

A description of freezing porous materials will invariably incorporate more than one physical field,such as a thermal-hydraulic(TH)coupled field or a thermal-hydraulic-mechanical(THM)coupled field model.Because of the high nonlinearity of the governing equations and complex boundary conditions,coupled models are generally solved numerically by the finite element method(FEM),finite difference method(FDM),or finite volume method(FVM).Those interrelated parameters in the freezing process over the computational domain could be acquired by solving the correspondent governing equations.There have been numerous numerical models developed over the past few decades for simulating the transfer of soil,water,and heat(Flerchinger and Saxton,1989;Guymon and Luthin,1974;Thomas,1985;Thomas and King,1991;Thomas and He,1995;Hanssonet al.,2004;Jansson,2012;Šimůneket al.,2016;Yuet al.,2020;Zhenget al.,2021).Generally,those models can be categorized into hydrodynamic models,rigid ice models,poromechanical models,and semi-empirical models.In the early stage of model development,soil freezing is mainly related to the heat and flow transport process,along with the interaction between these two fields,also known as coupled thermal-hydraulic(TH)analysis.It is believed that Harlan(1973)first proposed a coupled TH model based on hydrodynamic theory and analyzed the freezing-induced soil water redistribution.Several models were further developed to study moisture movement and storage in freezing soil by considering phase change(Guymon and Luthin,1974;Taylor and Luthin,1978).Guymon and Hromadka(1980,1984)presented a onedimensional frost heave model based on the thermodynamic model,in which frozen water exceeds the porosity of the soil,leading to heaving.Then they extended the model for two-dimensional applications.The characteristic of these models is that the ice pressure is usually assumed to be zero,or the changes in the ice pressure are ignored.This assumption is seldom questioned except in cases such as ground heaving(Hanssonet al.,2004).For the rigid ice model,it is assumed that soil ice grows and moves as a rigid body,and ice pressure is not necessarily zero.This type of model is put forward to physically model a special zone termed the frozen fringe in frost-heaving soil;also,initiation criteria and growth of discrete ice lens are well studied based on secondary heave theory(Gilpin,1980;O'Neill and Miller,1985;Nixon,1991).The semi-empirical model,also known as the segregation potential model,was originally proposed by Konrad and Morgenstern(1980,1981,1982).This model is developed based on the assumption that the frost heave rate is related to the temperature gradient.When the segregation potential,which depends on cooling rate,frost front suction and pressure(Nixon,1992),and the temperature gradient are available,the frost heave can be directly calculated.

The development of poromechanics offers a new approach for modeling porous materials exposed to freezing conditions.Based on Biot's theory of dynamic poroelasticity(Biot,1941),poromechanics gives a complete and general description of the mechanical behaviour of a poroelastic medium.One representative poromechanical model was developed by Coussy(2005)and Coussy and Monteiro(2008).To better understand the effects of frost expansion and stress,researchers have begun combining heat-moisture analysis with stress analysis(Neaupane et al.,1999;Liet al.,2000;Nishimuraet al.,2009;Thomaset al.,2009;Yu and He,2011;Zhou and Li,2012;Laiet al.,2014).These models provide insights into the thermohydro-mechanical behaviour of freezing soil,though most are set up for saturated soil.Different numerical models have been presented to explain moisture transport and soil-water characteristics as well as soil freezing characteristics since the 1970s(Harlan,1973;Spaans and Baker,1996;Hanssonet al.,2004).However,due to the high nonlinearity of governing equations induced by SWCC,SFCC,and nonlinear coefficients,few models exist that can simulate the freezing process of partially saturated soil.Besides,most of the proposed models are based on the non-isothermal consolidation of deformable porous media or an extension of Biot's phenomenological model and generally do not consider the phase change of water(Yu and He,2011).Therefore,a numerical model which includes ice-water phase change in partially saturated soil under the freezing process is needed.

2 Theory and governing equations

2.1 Assumptions and structure of the couple d model

To simulate transient,simultaneous heat and mass flow with phase change in frozen,partially saturated,homogeneous soil,the following assumptions are made:

(1)Darcy's law is applicable to moisture movement in both saturated and unsaturated conditions.

(2)The porous media is a non-deformable and isotropic material.

(3)The impact of the mechanical(M)field on thermal-hydraulic(TH)fields is ignored.

A schematic depicting the interaction between various physics fields in the proposed model is shown in Figure 1.The ignored coupled relationship between the mechanical field and thermal-hydraulic fields is illustrated as dash lines.)

Figure 1 Schematic interpretation of THM coupling

2.2 Governing equations

2.2.1 Thermal field

Based on the energy conservation principle,the partial differential equation(PDE)to describe the transient heat flow in the freezing process can be written as(De Vries,1958;Nassar and Horton,1989,1992):

whereCvis the volumetric heat capacity of the soil;Tis temperature;λis the thermal conductivity of the soil;Lfis the latent heat of fusion;ρiis the density of ice;andθiis the volumetric ice content.

2.2.2 Hydraulic field

Richard's equation was adopted to describe the flow in the partially saturated porous medium.In this study,a mixed form of Richard's Equation(Noborio,1996;Fayer,2000)was used,which can be written as

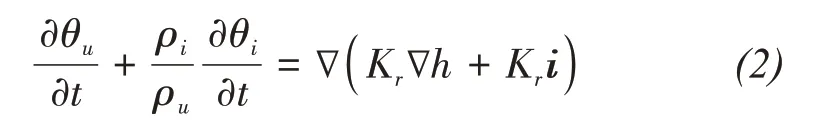
whereθuis the volumetric unfrozen water content;ρuis the density of water;Kris the hydraulic conductivity of the soil(unit:m/s);his the matric potential(unit:m);iis the unit vector along the direction of gravity.In this model,as the conduction influence on heat transfer and water migration is limited,most studies generally neglected it(Konrad,2005;Zhaoet al.,2013).

2.2.3 Mechanical field

According to Liu(2018),the linear elastic model is adequate for accurately simulating the freezing test of unsaturated soil.Therefore,to control the complexity of the model,such a model was used in this study to describe deformation during the freezing process.Navier's equation,which incorporates the equation of motion,strain,displacement correlation,and the constitutive relationship,serves as the governing equation in the mechanical field(Liu et al.,2020),

whereCis a fourth-order tensor of material stiffness;uis the displacement vector;Fis the body force vector.And the strain-displacement relationship can be expressed as follows,

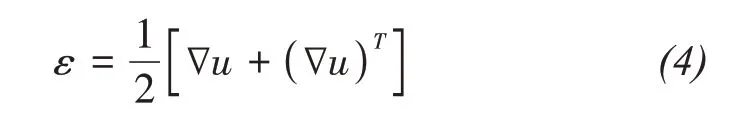
whereεis the infinitesimal strain tensor.

The simplified linear elastic constitutive equation can be derived as,

whereσis Cauchy stress tensor;Dis the stiffness matrix of soil skeleton;σ0is the initial stress vector;εel,εth,εtr,andεhpare the elastic strain,strain caused by thermal expansion,strain caused by water phase change,and strain caused by matric potential,respectively;andε0is the initial strain.εth,εtr,andεhpcan be separately expressed as follows(Liu,2011),

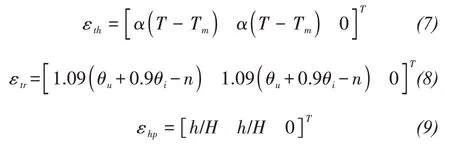
2.3 Coupled parameters

2.3.1 Thermal field coupled parameters

The thermal conductivity of the frozen and unfrozen soil can be generally expressed as follows(Côtéet al.,2005),

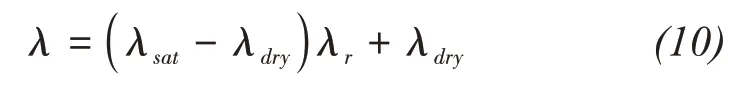
where,λsatis the thermal conductivity of saturated soil,λdryis the thermal conductivity of the dry soil,λris the normalized thermal conductivity,θuis the volumetric unfrozen water content.

The thermal conductivity of saturated soil and normalized thermal conductivity can be calculated by Equations(11)and(13)(Côtéet al.,2005).

whereK0is an empirical parameter depending on soil type.

The volumetric heat capacity can be calculated using the weighted algorithm as,

To reduce the nonlinearity,the concept of apparent heat capacity can be used to merge the heat capacity with the second term of Equation(1)on the right hand,which accounts for the enthalpy change due to phase change(Anderson,1973;Harlan,1973):

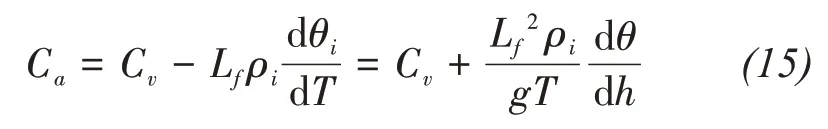
Thus,the volumetric ice content can be expressed as,

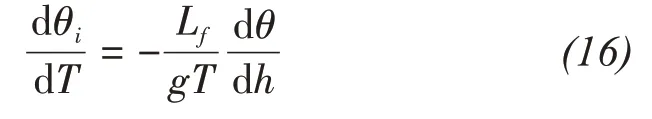
And the total volumetric water content is the sum of the volumetric ice content and the volumetric unfrozen water content:

By using the generalized Clapeyron equation,the apparent volumetric heat capacity can be redefined by the hydraulic capacityCHaccording to Hanssonet al.(2004).The hydraulic capacity is defined as the derivative of water content concerning the pressure head,which can be expressed as,

Therefore,Equation(15)can be rewritten as,

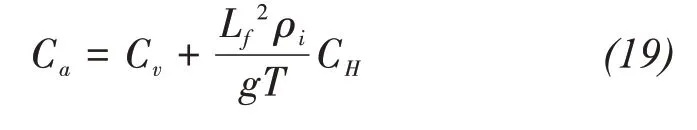
Unfrozen water can also co-exist with ice in unsaturated soil during freezing.At this time,soil water potential remains in equilibrium with the vapor pressure over pure ice(Flerchinger and Saxton,1989).Based on the thermodynamic relationship and the Clausius-Clapeyron equation,Dall'Amico(2011)proposed an equation to describe the relationship between soil matric potential and final freezing temperature in the freezing process.WhenT≥Tf,the soil is unfrozen;whenT＜Tf,the soil is under freezing conditions.

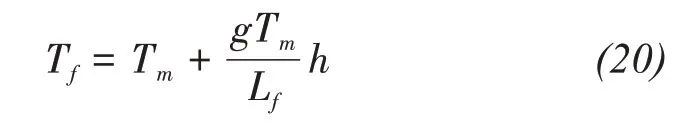
2.3.2 Hydraulic properties

For unfrozen unsaturated soil,the hydraulic conductivity can be expressed by using relative hydraulic conductivity,Kwr,which is a power function of the effective saturationSe,per the Mualem-van Genuchten model:

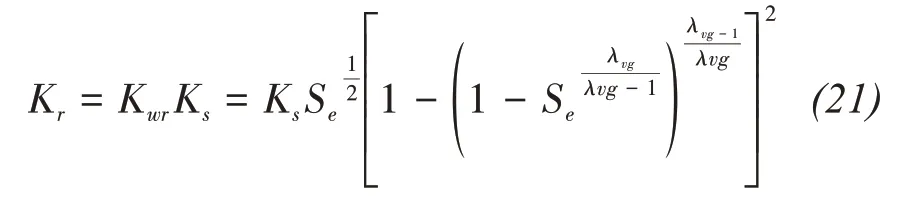
where

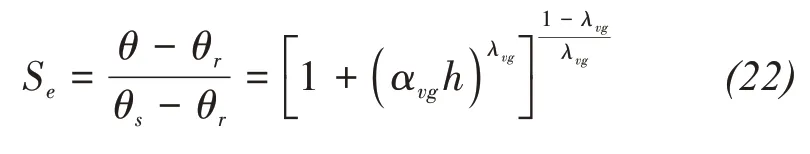
A characteristic of frozen soil is that its permeability decreases as ice saturation increases.Considering ice content,Jame and Norum(1972)suggested an impedance factor approach to describe the permeability in the freezing process:

Taylor and Luthin(1978)compared the simulation result with the data of Jame(1976),proposed and validated a relationship between the volumetric ice content and impedance factor,I,as follows.

The most common way to determineEiis proposed by Shoop and Bigl(1997):

Similarly,for unsaturated frozen soil,the permeability can be expressed as,

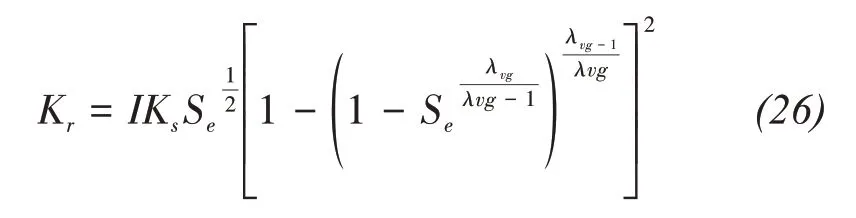
Supposehsis the saturated matric potential(i.e.,hs=0).Equations(21)and(23)are used to describe unsaturated soil permeability in the freezing process.Thus,the formulation of the permeabilityKrunder freezing conditions for saturated and unsaturated soils becomes:

2.3.3 SWCC and SFCC

In the unfrozen status,the soil-water characteristic curve(SWCC)is used to represent the relationship between suction and the volumetric water content.When the soil is saturated,the unfrozen volumetric water content can be expressed as the saturated volumetric water content.For the unsaturated condition,the hydraulic properties of unsaturated soil may be used to describe the volumetric water content.In this study,the Van Genuchten-Mualem Equation(Mualem,1976)with independent parametersαvgandnvgare used.

Meanwhile,a similar soil freezing characteristic curve(SFCC)is used to describe the relationship between temperature and suction in the freezing process.Assuming that the ice pressure is zero,Hansson(2004)proposed a generalized Clapeyron equation based on the thermal dynamic equilibrium theory.The Clapeyron equation can be used to convert sub-freezing temperature to suction.Based on this theory,the SFCC can be derived from SWCC by relating suction with sub-freezing temperature.When the temperature is under the freezing point,the following equation can be used to evaluate the soil matric potential:

3 Numerical model and parameters

Frost heave simulations with three types of frost susceptible soils were performed under various test conditions,including overburden pressure(σob),water supply(closed-system/open-system),cooling rate(U),and initial saturation(S0).Figure 2 presents the size of the model domain,boundary conditions,and the finite element mesh of the two-dimensional model under a plane strain condition.The boundary conditions of each field follow the actual test conditions.Note that the hydraulic boundary on the top surface depends on the water supply(open-system or closed-system)used in each experiment.The COMSOL software,a commercial multiphysics simulation platform,was used to solve the coupled model.

For the thermal field,the soil was frozen from the bottom up.Thus,the adiabatic boundary was imposed on both lateral sides,a constant thermal boundary was imposed on the top surface,and a constant cooling rate U was imposed on the bottom.For the hydraulic field,the impermeable boundary was imposed on both lateral sides and the base.Herein,an open system permits free intake and discharge of water by setting a constant hydraulic pressure boundary on the top surface,whereas the closed system prohibits water intake by setting an impermeable boundary on the top surface.For the mechanical field,the bottom was fixed in both vertical and horizontal directions,and both lateral side boundaries were fixed in the horizontal direction,while a prescribed overburden pressure was applied on the top surface.

The model developed herein was applied to a typical THM freezing process,and the simulation results were compared against the experimental results from Tokoroet al.(2016)and Ishikawa(2015).Three typical frost susceptible soils were used in the simulation,including Fujinomori soil(medium frostsusceptible soil),Touryo soil(high frost-susceptible volcanic soil),and Tomakomai soil(medium frostsusceptible soil).Note that Fujinomori soil is composed of 18% clay,78% silt,and 4% sand,Tomakomai soil consists of 3% clay,19% silt,and 78%sand,and Touryo soil comprises 26% clay,21% silt,and 53% sand.Table 1 summarizes the parameters used in this study.

Dry density and porosity are the averaged values of all the tested specimens.Each VGM parameter of the three types of soils is fitted based on water retention test data(Ishikawaet al.,2015).The saturated hydraulic conductivity for each soil was obtained by permeability tests(Nakamuraet al.,2011;Uedaet al.,2005).However,values recommended by Guymonet al.(1993)were used for the thermal conductivity and volumetric heat capacity of soil particles.Additionally,the thermal expansion coefficient of water was set to zero to ignore thermal expansion,which is considered to have a marginal influence on the frost behavior of soil.Other parameters were based on previous studies(De Vrieset al.,1983;Fredlundet al.,1993;Liuet al.,2011;Ishikawaet al.,2016;Luoet al.,2017;Stuuropet al.,2021).

Figure 2 Model domain,mesh and boundary conditions for frost heave simulations

Table 1 List of input parameters

4 Experimental data for model evaluation

4.1 Test apparatus

An illustration of the frost heave testing apparatus is shown in Figure 3.The apparatus has two thermostatic baths,which,by circulating antifreeze liquid at a specific temperature,control the temperature of the cap and pedestal independently.A platinum resistance thermometer was used to measure the temperature in the apparatus.In this way,any temperature difference between the cap and the pedestal might be set arbitrarily.To further control the specimen temperature,cold water at 2 degrees Celsius was circulated between the inner and the pressure cells,and thermally insulating materials were placed between the frost-heave and inner cells.A pneumatic actuator was used to apply overburden pressure in the range of 0 to 130 kPa.To examine the temperature distribution,three sheath-type thermocouples located at heights of 0.75 cm,2.18 cm,and 3.58 cm from the specimen bottom,respectively,were inserted into the specimen through the frost-heave cell.In addition,the inflow and outflow of water were determined using a differential transducer connected to a double tube burette.

Figure 3 Frost heave test apparatus:(a)general view;(b)temperature measurement locations within a specimen

4.2 Model validation

The numerical simulation results were compared against the frost heave test data using Touryo soil by Ishikawaet al.(2015)and Fujinomori soil by Tokoroet al.(2006)to verify the model.In this study,the numerical model boundary conditions were as follows:the cooling rate was set as-0.2℃at the pedestal and the cap temperature as 0.1℃;the overburden pressure was set as 10 kPa on the top surface;a permeable boundary was used at the top surface.

As shown in Figure 4,the trends of the frost heave and water migration in the numerical simulation agree very well with those in the experiment.It also can be seen that the frost heave ratio increases with the water intake amount,indicating that sufficient water supply is a critical factor for ice growth and frost heave.Although the frost heave ratio and the amount of water intake are overestimated at the beginning of freezing,the difference between test and simulation results decreases as the freezing process proceeds.Zhaoet al.(2013)and Yuet al.(2020)also reported similar phenomena and attributed the overestimation in the early freezing stage to the sudden ice-water phase transition.

Figure 4 Comparison between the numerical and experimental results of frost heave tests for Touryo soil

Two Fujinomori soil columns were forced to freeze under controlled boundary conditions in the experimental study of Tokoroet al.(2006).In this paper,by using the setup in their study,the soil columns were initially saturated.The cooling rate applied on the pedestals was-0.075℃/h while the cap temperature remained 0.1℃.Moreover,different overburden pressures,i.e.,50 kPa and 100 kPa,were set on the top boundary of the samples.As shown in Figure 5,the numerical model results are in good agreement with the experimental values.Under both overburden pressures,the simulation results for the water intake of Touryo soil are in good agreement with the test results.Due to the sudden ice-water phase transition,the simulated frost heave strain values of Touryo soil are also somewhat overestimated at the beginning of freezing.However,as freezing progresses,the difference between numerical and experimental results gradually diminishes.

Figure 5 Comparison between the numerical and experimental results of frost heave tests for Fujinomori soil

4.3 Simulation results

Frost heave tests of Touryo soil and Tomakomai soil under different conditions were conducted for 60 hours to collect data for examining the proposed model's stability.The testing parameters for a total of 12 experiments are summarized in Table 2.

Table 2 Experimental conditions

4.3.1 Closed-system frost heave tests

Figure 6 shows the comparison between measured and simulated frost heave ratios under different overburden pressures in the closed-system frost heave tests.The numerical models performed well in the simulations with two soil types.According to the simulation results,the frost heave amounts under 15 kPa are almost identical for Touryo and Tomakomai soil.In addition,it can be seen that the higher the overburden pressure was applied,the smaller the frost heave occurred,as the overburden pressure generated an initial strain shown in Equation(5).

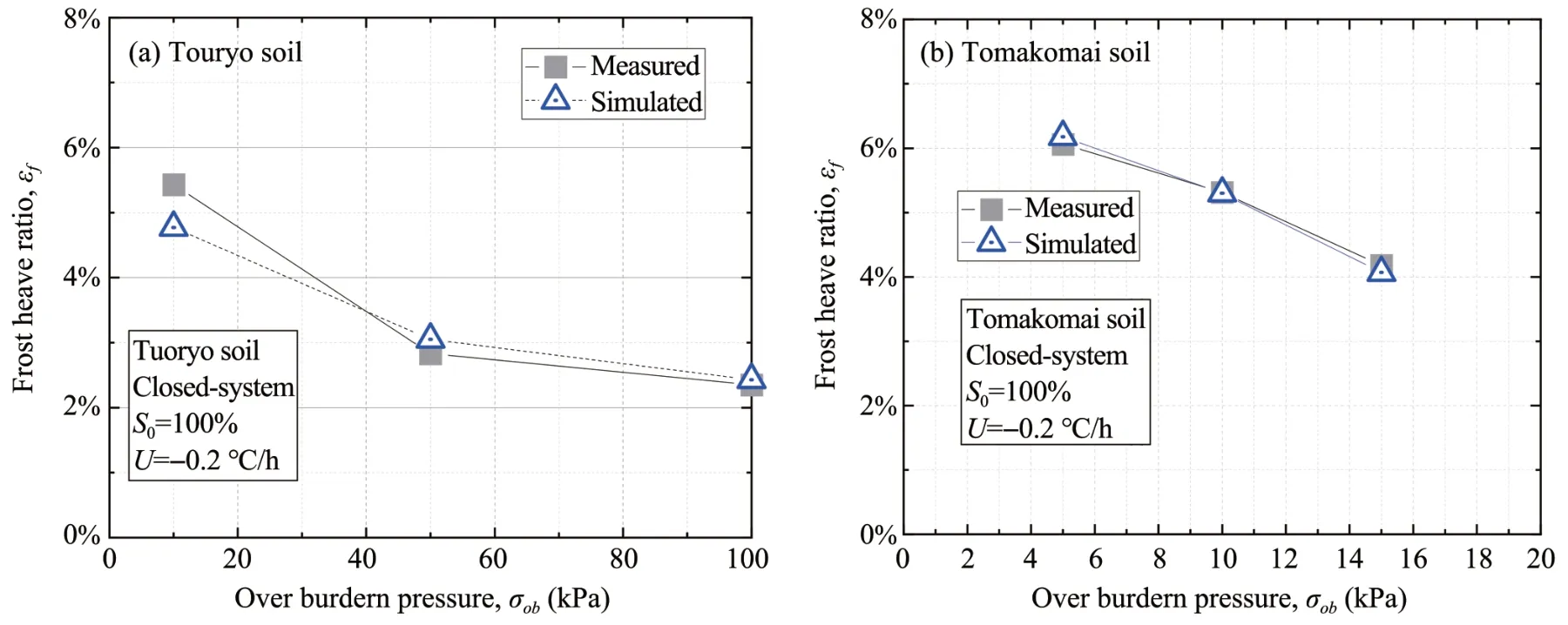
Figure 6 Influence of overburden pressure on frost heave in closed-system tests

Figure 7 compares the frost heave ratios of Touryo and Tomakomai soil from the simulations and experiments under the various initial saturation in the closed system.The comparations show that the simulation results agree well with the test data.Moreover,lower initial saturation leads to a smaller frost heave ratio since lower water content allows less water migration to the freezing front.

Figure 7 Influence of initial degree of saturation on frost heave in closed-system tests

4.3.2 Opened-system frost heave tests

Figure 8 illustrates the influence of overburden pressure on frost heave in the open system.The simulation results are close to the measured data.Moreover,the impact of overburden on frost heave is noticeable;the larger the overburden pressure is applied,the smaller the frost heave amount is generated.Meanwhile,the frost heave in the open system is much larger than in the closed system under the identical overburden pressure,as free water supply enables more ice accumulation.

Figure 9 shows the influence of cooling rate on frost heave in an open system.The simulation results agree well with the test data.Meanwhile,the cooling rate has an obvious effect on frost heave,which shows higher cooling rate leads to less frost heave ratio.The unfrozen water tends to migrate to the freezing front driven by the cryogenic suction during freezing.Under a high cooling rate,the freezing front proceeds quickly from the cold end to the warm one of the specimen,which does not allow enough time for unfrozen water to migrate to the freezing front and accumulate ice.On the contrary,when the cooling rate is low,a large amount of unfrozen water can migrate to the freezing front and form ice lenses,resulting in a larger amount of frost heave.

Figure 8 Influence of overburden pressure on frost heave in open-system tests

Figure 9 Influence of cooling rate frost heave in open-system tests

Figure 10 depicts the influence of the initial saturation on frost heave in the open system.The simulation results fit the experimental results well.Higher initial saturation for both Touryo and Tomakomai soil leads to a more significant frost heave than lower initial saturation.The high frost heave amount is attributed to the higher water content.This tendency can be observed more clearly in Touryo soil,which has higher initial and residual degrees of saturation compared with Tomakomai soil.Larger initial and residual degrees of saturation indicate more pore water in Touryo soil.With negligible hydraulic permeability,the unfrozen water is harder to drain out than Tomakomai soil.

4.4 Typical parameters analysis

A closed-system frost heave test of fully saturated Touryo soil was chosen as the prototype for the computational model construction in the simulation to reproduce the freezing process and examine the frost heave mechanisms.The specimen was frozen from the bottom up,with the pedestal temperature dropping from 0 °C to-3 °C in 15 hours and the cap temperature remaining 0.1 °C,while all boundaries were kept impermeable.The sample was thermally insulated on the sides.Furthermore,a constant overburden pressureσobof 10 kPa was applied on the top surface.

The unfrozen zone is the area free of ice.Once ice starts to form,the area is considered to be a frozen zone.As shown in Figure 11,the temperature changes rapidly in the frozen zone,while the temperature becomes steady in the unfrozen zone due to the ice formation.Since the thermal conductivity of water is lower than that of ice,the heat transfer in the frozen zone is easier than in the unfrozen area,resulting in different temperature gradients in the frozen and unfrozen zones.In the unfrozen zone,the total water content(water and ice)always coincides with the unfrozen water content since the ice content remains zero.The unfrozen water content drops in both frozen and unfrozen zone while ice content increases in the frozen zone.The total water content is much higher in the frozen area than in the unfrozen area,illustrating significant moisture migration from the unfrozen area to the freezing front driven by cryogenic suction gradient during freezing and leading to ice accumulation nearby.

Figure 10 Influence of initial degree of saturation on frost heave in opened-system tests

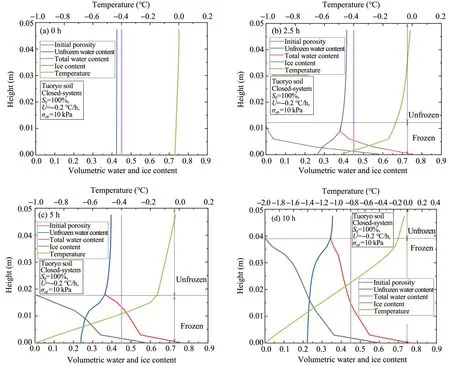
Figure 11 Evolution of volumetric water and ice content and temperature with freezing time

Suction,saturation,and relative hydraulic conductivity are the main factors that affect water migration.The evolution of these factors during 10 hours of freezing is depicted in Figure 12.In saturated conditions,the initial porosity dictates the volumetric water content.It can be seen that the cryogenic suction increases sharply while the relative hydraulic conductivity decreases rapidly in the frozen area,resulting in a significant rise in the total water content near the freezing front,as shown in Figure 13.Here,Figure 13 presents the volumetric unfrozen water and ice content and deformation profiles after 0,2.5,5,10 hours of freezing.Moreover,as the relative hydraulic conductivity decrement is more significant than the porewater pressure increment,water is hard to migrate in the deeper frozen area.Therefore,the ice content in the deeper frozen area increases slower than in the freezing front.

Figure 12 Development of the suction and relative hydraulic conductivity profiles with freezing time

The unfrozen water content in the unfrozen zone decreases gradually while the deformation increases as the frozen zone expands.Figure 13 shows that there exists a maximum value along with the height of the specimen.During the freezing process,the unfrozen water migrates to the freezing front and is transferred into ice.The excessive water and ice content enlarge the specimen.Meanwhile,as unfrozen water migrates to the frozen fringe,the water content in the unfrozen zone decreases.Under the overburden pressure,the deformation of the soil above the freezing front is suppressed.In addition,Figure 13 shows that in the frozen zone,the frost heave grows faster during the early freezing process(from 0 to 2.5 h)than at the end of freezing(from 5 to 10 h).And,It is attributed to the fact that,as the frozen zone expands,the water content and permeability in the unfrozen zone continue to decrease,rendering less water available for migration and making it difficult for water to migrate to the freezing front and form ice lens.

Figure 13 Evolution of the volumetric unfrozen water and ice content profile and frost heave ratio with freezing time

Simulating the freezing process generally incurs high computational cost and numerical instabilities because of the highly nonlinear relationships between unfrozen water content,ice content,water head,temperature,and hydraulic conductivity caused by substantial latent heat and phase change.The proposed numerical model performed well for all the test problems and is suitable for many different experimental conditions.

5 Conclusions

In this study,a coupled THM model was proposed to simulate partially saturated soil in the freezing process.The conclusions from this study are summarized as follows.

(1)The proposed model can capture the main features of unsaturated soil during freezing,such as suction-induced freezing point depression,water redistribution caused by cryogenic suction gradient,and,most importantly,frost heave.

(2)Parametric analysis indicates that the frost heave ratio is proportional to the initial degree of saturation,and it is inversely proportional to the cooling rate and overburden pressure.Moreover,simulation in the open system generates much more frost heave compared with that in the closed system.

(3)The validity of this model is confirmed by comparing the simulated frost heave ratio and water migration amount with those of the test data.The proposed model performs well in predicting the frost heave and water migration amount for different soils.

Acknowledgments:

This research was supported in part by Grant-in-Aids for Scientific Research(A;16H02360)and(B;17H03307)from the Japan Society for the Promotion of Science(JSPS)KAKENHI.The authors also acknowledge the financial support from the China Scholarship Council.