聚焦逻辑推理素养的深度学习*
——以二次三项式的判别式证明著名不等式为例
2023-01-02北京市第一0一中学怀柔分校101407李加军
北京市第一0一中学怀柔分校(101407) 李加军
我国《普通高中数学课程标准(2017 年版)》明确指出:“在学习数学和应用数学的过程中,学生能发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养.”
数学核心素养是以数学课程教学为载体,基于数学学科的知识技能而形成的重要的思维品质和关键能力.数学核心素养是在数学知识技能的学习过程中形成的,有助于学生深刻理解与掌握数学知识技能.数学核心素养不等同于数学知识技能,是高于数学知识技能的,指向于学生的一般发展,反映数学学科的本质及其赖以形成与发展的重要思想,有助于学生终身和未来发展.数学核心素养与数学课程的目标和内容密切相关,对于理解数学内容的本质,设计数学教学,以及开展数学学习评价等,有着重要的意义和价值.
逻辑推理是指从一些事实和命题出发,依据逻辑规则推出一个命题的思维过程.主要包括两类: 一类是从特殊到一般的推理,推理形式主要有归纳、类比;一类是从一般到特殊的推理,推理形式主要有演绎.逻辑推理是得到数学结论、构建数学体系的重要方式,是数学严谨性的基本保证,是人们在数学活动中进行交流的基本思维品质.在逻辑推理核心素养的形成过程中,学生能够发现问题和提出命题;能掌握推理的基本形式,表述论证的过程;能理解数学知识之间的联系,建构知识框架;形成有论据、有条理、合乎逻辑的思维品质,增强数学交流能力.
深度学习,是指在教师引领下,学生围绕着具有挑战性的学习主题,全身心积极参与、体验成功、获得发展的有意义的学习过程.在这个过程中,学生掌握学科的核心知识,理解学习的过程,把握学科的本质及思想方法,形成积极的内在学习动机、高级的社会性情感、积极的态度、正确的价值观,成为既具独立性、批判性、创造性又有合作精神、基础扎实的优秀的学习者,成为未来社会历史实践的主人.
一元二次方程ax2+bx+c=0(0,a,b,c ∈R)的判别式∆=b2−4ac是判断方程是否有实根的重要依据,贯穿于初高中的数学学习之中.下面结合几个典型案例探索利用判别式证明不等式,将有助于扩展学生的知识面并培养举一反三、触类旁通的能力,提高学生自我研究创新能力,对发展学生的数学核心素养大有裨益.
首先,如果一元二次函数f(x)=ax2+bx+c(a >0,a,b,c ∈R) 对∀x ∈R 都有f(x)>0(或f(x) ≥0),则∆=b2−4ac<0(或∆=b2−4ac≤0).

这样,就是由若(3)式取等号,推导得(4)成立,反之,由(4)易于推导出(3)式取等号.
例2(积分不等式) 已知非零函数f(x),g(x) 在区间[a,b]上连续可积,则
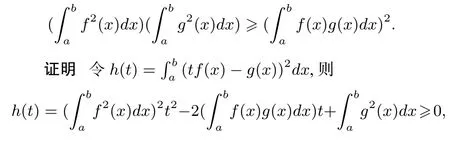

例3(方差不等式) 设X,Y是两个随机变量,则D(X)D(Y)≥[E(X −EX)(Y −EY)]2,其中E(X),D(X)分别表示变量X的期望和方差.

其次,如果一元二次函数f(x)=ax2+bx+c(a >0,a,b,c ∈R) 的判别式满足∆=b2−4ac <0(或∆=b2−4ac≤0),则对∀x ∈R 都有f(x)>0(或f(x)≥0).
例4(三角形嵌入不等式) 对于任意∆ABC的三个内角A,B,C和任意实数x,y,z,有x2+y2+z2≥2xycosC+2yzcosA+2zxcosB.等号成立当且仅当
证明原不等式转化为x2+y2+z2−2xycosC −2yzcosA −2zxcosB≥0,构造二次函数f(x)=x2−2x(ycosC+zcosB)+y2+z2−2yzcosA,因为

所以f(x) ≥0 恒成立,所以原不等式得证.等号当且仅当∆=0,即ysinC −zsinB=0 取到,进而可知等号成立当且仅当
再者,如果一元二次函数f(x)=ax2+bx+c(a >0,a,b,c ∈R),∃x0∈R 使得f(x0)<0(或f(x0) ≤0),则∆=b2−4ac>0(或∆=b2−4ac≥0).



例7(康托洛维奇不等式,n=3 是1979 年北京市数学竞赛题) 已知a1,a2,···,an为正数,λ1,λ2,···,λn为 实 数(i=1,2,···,n),且a1+a2+···+an=1,0<λ1≤λ2≤···≤λn,求证

深度学习的提出,既是对教学规律的尊重,也是对时代挑战的主动回应.事实证明,发展学生数学核心素养正是深度学习的目标指向,而真正意义的深度学习,也必然是指向学生数学核心素养养成的学习.
