一种基于轮胎独立转向的跨运车变道轨迹规划方法*

朱 娜 刘春明

上海振华重工(集团)股份有限公司

1 引言

集装箱跨式运输车(以下简称跨运车)，主要应用于集装箱码头以及集装箱中转堆场中。与其他自动化水平运输车辆相比，自动化跨运车具备完成多种作业任务的能力[1]。它可以完成从码头前沿到码头堆场的水平运输集装箱作业，以及进入堆场后的装卸、搬运和堆垛集装箱作业，实现抓取集装箱、卸载集装箱、水平运输集装箱和垂直码垛集装箱等功能于一体[2]。跨运车因具有轮胎压力低、稳定性能好、机动灵活高效等特性，可有效提高码头前沿的装卸效率[3]。

轨迹规划的本质是针对多目标运行轨迹进行数学优化，得出运动物体，特别是移动机器人的未来运动轨迹。该轨迹与障碍物无碰撞，可执行，包含路径信息和速度信息，尽可能高效地使物体从起始点运动到目标点。移动车辆的轨迹规划是生成未来一段时间内的移动车辆的行驶轨迹[4-5]。移动车辆的轨迹规划方法包括全局规划和局部规划。全局规划是个整体规划问题，即在整体的环境下寻找出从起始点到最终点的最优路径；局部规划是全局路径中的部分轨迹规划问题。全局轨迹规划寻求全局最优，局部路径规划寻求局部最优。

移动车辆的全局轨迹规划方法主要有Dijkstra算法、A*算法、智能仿生算法等。Dijkstra算法是搜索图形中的节点之间最短路径的方法，它从起始点出发，一层一层地向外扩展，一直到目标点为止，停止扩散[6]。在扩展过程中，该算法寻找出与访问过的节点距离最小的尚未访问过的节点，然后利用该节点，更新其他节点的距离值，是一种盲目式搜索算法。A* 算法利用启发式函数，结合广度优先搜索算法和Dijkstra算法，能够更快的找到图形中的节点之间的最优路径，是直接搜索静态路网中最短路径的最有效方法[7]。智能仿生算法是模仿生物行为的方式来获得全局最优路径，典型的是蚁群算法。蚁群算法以模仿蚂蚁集群觅食行为的方式，来获取全局规划结果。当蚂蚁在觅食时，它会在已经走过的路径上留下分泌的信息素，后来觅食的蚂蚁就会根据信息素的启发来决定自己的行为轨迹，把搜索到的信息素浓度最高的路径作为自己的期望路径，即近似最优路径。蚂蚁群法得到的次优路径通常会受蚂蚁的数量、信息素的数量以及启发因子的影响[8]。

移动车辆的局部轨迹规划方法主要有模拟退火法和人工势场法等。模拟退火法是从某一个比较高的温度开始，随着温度参数的持续下降,按照一定的概率发生突跳，在问题空间中随机寻找目标函数的局部最优解。它是一种通用的概率演算方法，简单有效，控制的参数相对较少，但会出现速度变慢等问题[9]。人工势场法是将移动车辆所在的环境看成一种抽象的势场，通过目标点对移动车辆的引力和障碍物对移动车辆的斥力来决定运动的方向，即通过引力和斥力的合力来确定移动车辆的运动。人工势场法的优点是结构简单，易于实时控制，得到的路径通常比较平滑，但容易陷入局部最优或局部震荡的情况[10]。

港口中的自动化跨运车通过接收中控的指令来完成无障碍的局部驾驶任务，故其轨迹规划通常为局部的、无障碍的、可执行的轨迹规划，规划的轨迹类型主要包括直行轨迹，转弯轨迹和变道轨迹。针对变道轨迹规划进行研究，根据给定的变道距离和行驶速度，以及在保证转向角变化率可以满足执行器限制的条件下，选择转向角的上限值，给出了变道轨迹的详细设计方法，并进行仿真实验，证明了轨迹规划方法的有效性。

2 跨运车变道轨迹规划方法

轮胎独立转向的跨运车是通过轮胎的滚动来进行行走运动，其中每个轮胎的转向角度都是独立的，转向角度可通过转向机构进行控制。因此，跨运车的运动学模型可简化为图1所示，其中，跨运车的长度为L，跨运车的宽度为W，跨运车6个轮胎的转向角度分别为θi(i=1,2,…,6)。跨运车的轨迹规划主要是对轮胎的转向角进行规划。

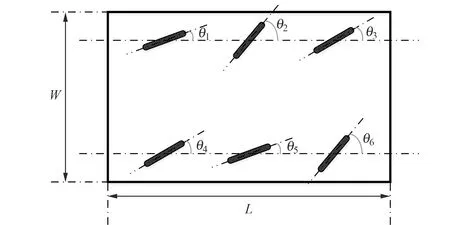
图1 跨运车运动学简化模型

2.1 变道过程中的轮胎转向角规划

在跨运车变道轨迹规划方法中，令6个轮胎的转向角度在任意时刻均相等，即：

θ1=θ2=θ3=θ4=θ5=θ6=θ

(1)

式中，θ为跨运车外轮廓等效中心点C处的虚拟轮胎摆角(见图2)。

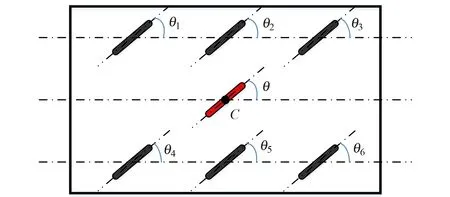
图2 跨运车等效中心点C处的虚拟轮胎及摆角θ

跨运车在变道过程中有3种状态：初始状态、中间状态和终止状态(见图3)。在初始状态和终止状态中，跨运车的轮胎摆角满足θ1=θ2=θ3=θ4=θ5=θ6=θ=0；在中间状态中，跨运车的轮胎摆角满足θ1(t)=θ2(t)=θ3(t)=θ4(t)=θ5(t)=θ6(t)=θ(t)≠0。在跨运车的初始状态处，建立直角坐标系OXY，其中原点O位于跨运车的等效中心点C处，OX轴与车辆的纵向中心线平行，OY轴指向车辆的侧向。跨运车的变道轨迹在初始时刻需满足：

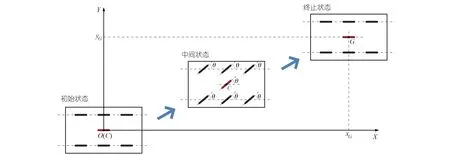
图3 跨运车变道过程中的3种状态

(2)

式中，xC为点C的横坐标，yC为点C的纵坐标。跨运车的变道轨迹在终止时刻需满足：

(3)

式中，xG为跨运车变道轨迹的目标点G的横坐标，yG为点G的纵坐标。

设跨运车在进行变道运动时，其轮胎的平移速度为v，点C的坐标变化应满足：

(4)

将轮胎的转向角θ设计为“加速-保持-减速”的3段形式，对应着3个角度变化的阶段：①转向角θ线性增加阶段tup，②转向角θ保持最大摆角θmax阶段thold，③转向角θ线性减小阶段tdown(见图4)。

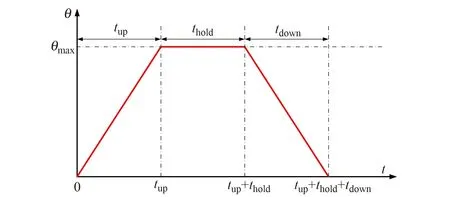
图4 跨运车变道过程中的轮胎转向角规划

2.2 转向角θ线性增加阶段

在转向角θ线性增加阶段，跨运车的轮胎转向角：

θ(t)=kθtt∈[0,tup]

(5)

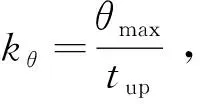
(6)

从公式(6)中，可以得到该阶段的初始坐标xC(0)=0，yC(0)=0，以及该阶段的终点坐标：

(7)

该阶段中的点C坐标还满足：

(8)

2.3 转向角θ保持最大摆角阶段

在转向角θ保持最大摆角θmax阶段，跨运车的轮胎转向角：

θ(t)=θmaxt∈[tup,tup+thold]

(9)

此时点C的坐标为：

(10)

(11)

该阶段中的点C坐标还满足：

yC(t)=tanθmaxxC(t)+yC(tup)-tanθmaxxC(tup)

(12)

即该阶段的轨迹为一直线段，其斜率为tanθmax，截距为yC(tup)-tanθmaxxC(tup)，起始点为(xC(tup),yC(tup))，终止点为(xC(tup+thold),yC(tup+thold))。

2.4 转向角θ线性减小阶段

转向角θ线性减小阶段的时长设计成与增加阶段的时长相等，即tdown=tup，那么跨运车的轮胎转向角为：

θ(t)=kθ(2tup+thold-t)t∈[tup+thold,2tup+thold]

(13)

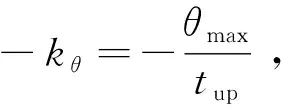
(14)

进而点C的坐标满足：

(15)

该阶段的初始坐标为(xC(tup+thold),yC(tup+thold))，利用公式(15)可以得到该阶段的终点坐标：

(16)

该阶段终点点C坐标还满足：

(17)

把式(11)代入有：

(18)

3 变道轨迹规划步骤

首先，明确跨运车变道轨迹的速度v，轮胎转向角的最大转向角度θmax，跨运车变道轨迹的目标点G的坐标(xG,yG)。

然后，利用方程组：

(19)

求解参数kθ和thold：

(20)

计算tup和tdown：

(21)

最后，得到跨运车的变道轨迹为：

4 变道轨迹的仿真实验

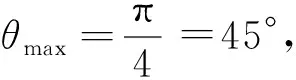
然后，计算参数kθ、tup、tdown和thold：

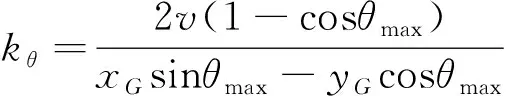
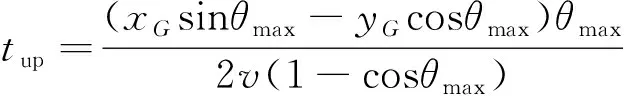
=4.485 3 s

tdown=tup=3.792 2 s

通过参数kθ、tup、tdown和thold，可以得到该变道轨迹对应的跨运车轮胎转向角θ的变化曲线(见图5)。

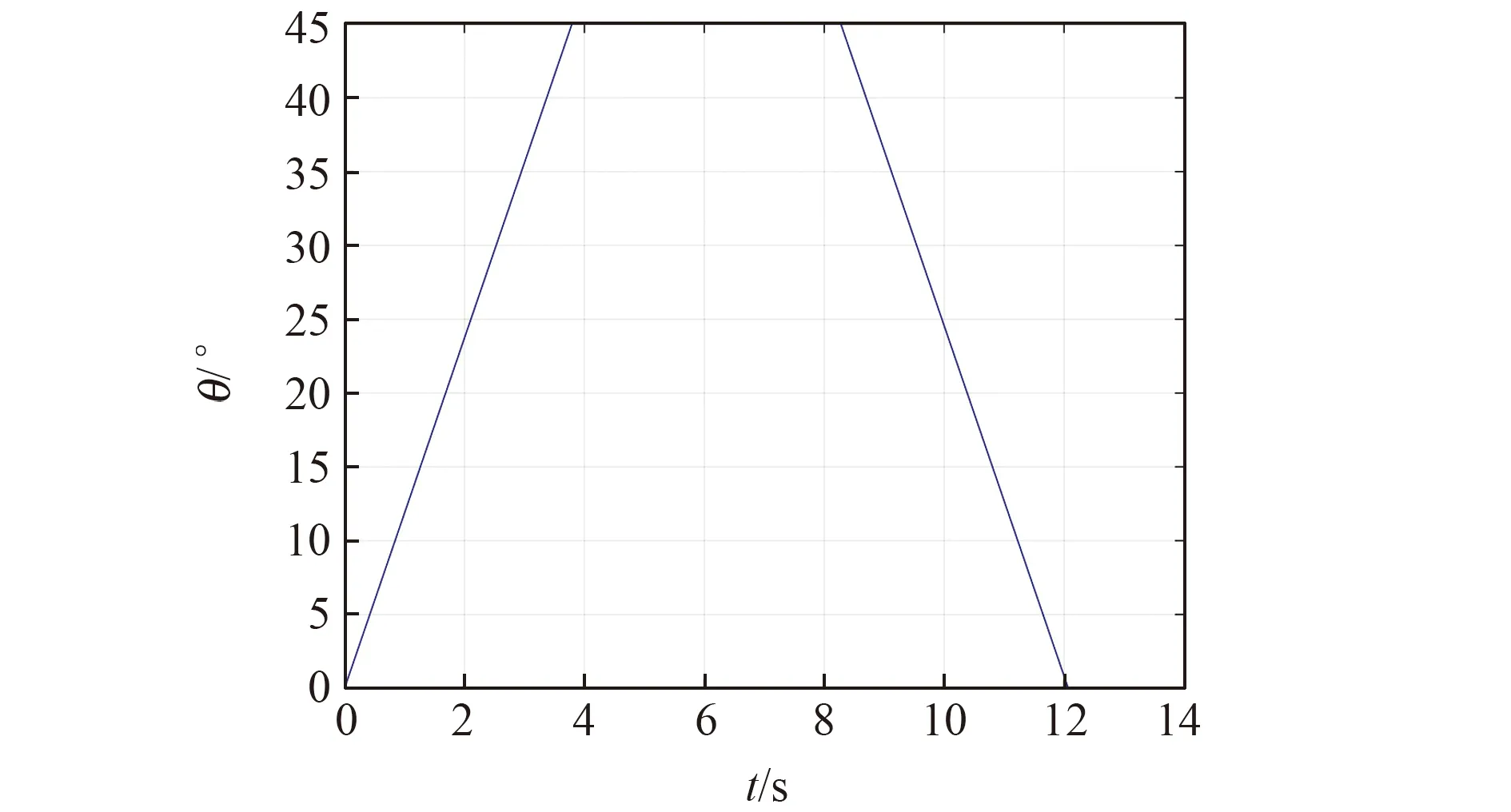
图5 跨运车变道轮胎转向角θ的变化曲线

最后，得到跨运车的变道轨迹见图6。第一段圆弧：圆心为(0,4.828 4)，半径为4.828 4，起始点为(0,0)，终止点为(3.414 2,1.414 2)。第二段直线段：斜率为tanθmax=1，截距为-2，起始点为(3.414 2,1.414 2)，终止点为(6.585 8,4.585 8)。第三段圆弧：圆心为(10,1.171 6)，半径为4.828 4，起始点为(6.585 8,4.585 8)，终止点为(10,6)。假设跨运车的外形尺寸为8 m×4 m，按照规划的变道轨迹行驶，得到了跨运车外轮廓的变化序列见图7。

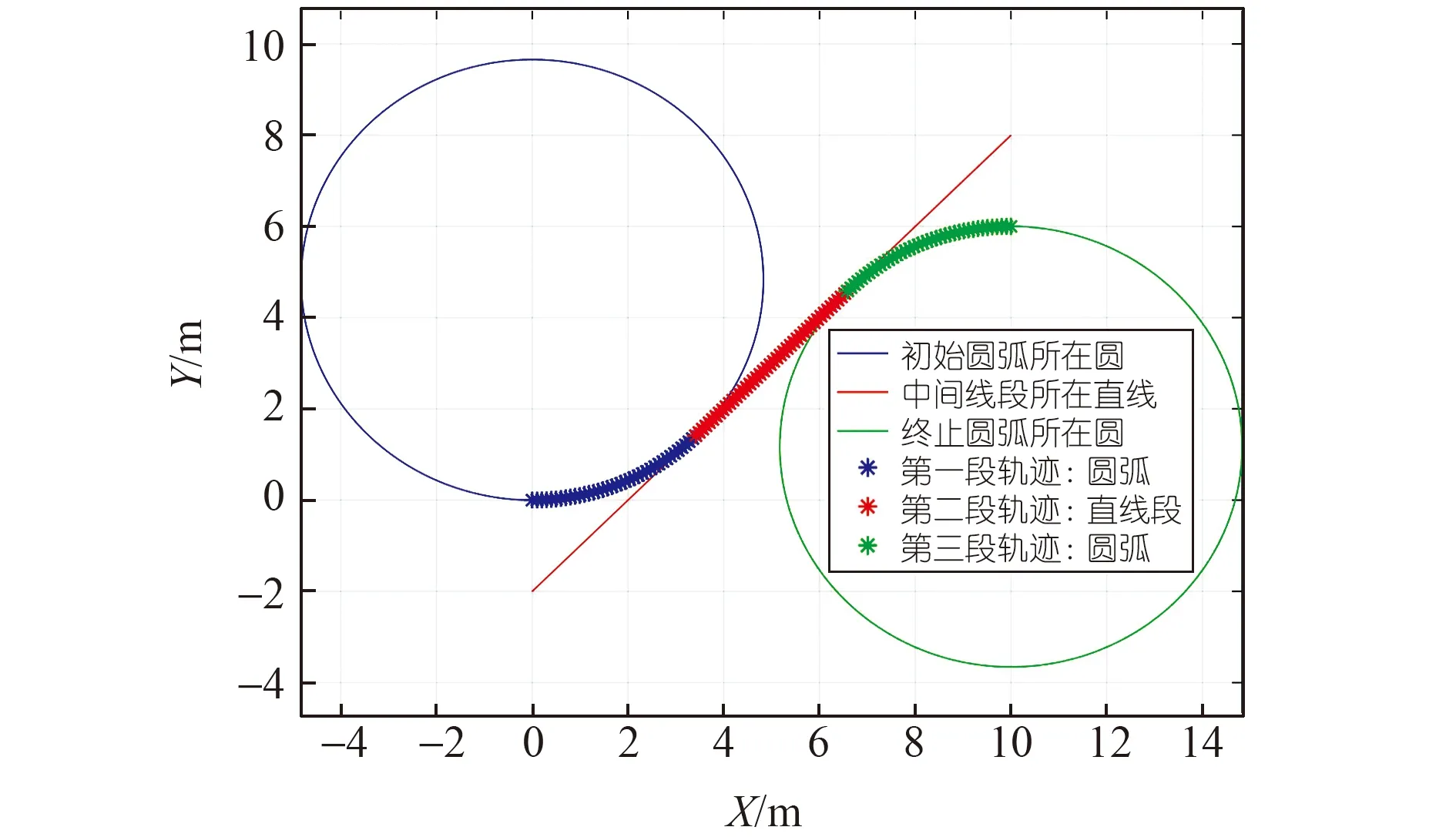
图6 跨运车变道轨迹的规划结果

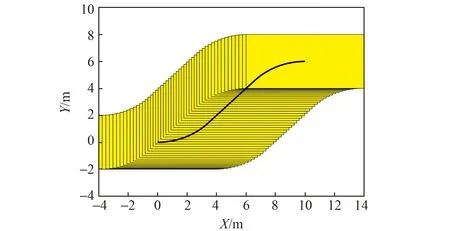
图7 跨运车按照变道轨迹行驶的外轮廓序列

5 结语

通过分析跨运车的轮胎转向结构，等效虚拟中心处的轮胎转向，简化了跨运车变道轨迹规划的方式，提出了一种基于轮胎独立转向的跨运车变道轨迹规划方法。该方法规划出的变道轨迹由圆弧-直线-圆弧三部分组成，形式简单、灵活，可以满足跨运车变道的行驶控制需求。