基于一种改进本构模型的橡胶超弹性温度相关性研究

2022-12-30付鑫涛王泽鹏马连湘

青岛科技大学学报（自然科学版） 2022年6期

付鑫涛,王泽鹏,马连湘

(青岛科技大学机电工程学院,山东青岛 266061)

橡胶基材料广泛应用于各种工业应用中。在这些应用中,橡胶部件在一定温度范围内承受各种载荷条件[1]。弹性元件温度过高可能是由周围环境或循环荷载期间内部耗散产生的固有加热引起的。此外,橡胶的低导热性加剧了这种情况[2]。研究硫化橡胶在不同温度下的力学行为,特别是在一定的高温范围内的力学行为,具有十分重要的意义。填充橡胶本构行为的温度依赖性是影响橡胶性能的重要因素。然而,目前研究应力-温度关系的本构模型还很少。

尽管填充和未填充橡胶在室温下的力学响应已经得到了表征[3-4],但在一定的变形范围内,如150%的应变下,温度对橡胶材料力学响应的影响还很少被研究。特别是,橡胶的工作温度通常在很大范围内,这取决于应用。大多数橡胶类材料的拉伸试验仅在室温下进行[5],因此,有必要研究这些材料在除室温以外的各种温度下的性能。此外,温度的变化会影响填料和橡胶基体之间的相互作用。从以前的研究来看,填充橡胶表现出更复杂的温度依赖特性,橡胶材料的性能显著依赖于温度[6-7]。重要的是建立一个本构模型,可以清楚地揭示和描述弹性元件的温度特性。

综上所述,基于Arruda-Boyce模型[8],即八链模型,发展了一种新的改进的八链模型,对4种填充有不同含量新工艺炭黑的橡胶在不同温度下进行了一系列单轴拉伸试验。基于准确的实验数据,讨论了温度对橡胶复合材料力学性能的影响,对改进的八链模型描述不同温度下橡胶实验数据的能力进行了评估,同时还讨论了改进八链模型参数的温度相关性。

1 温度对橡胶超弹性力学行为影响的实验研究

1.1 实验方案

采用4种不同含量炭黑填充的橡胶材料,橡胶基体均为天然橡胶,填充炭黑均为N234。4种橡胶的配方,只有炭黑的填充量不同。4种橡胶C0～C60中炭黑的质量填充份分别为0、20、40、60份。实验用4种橡胶的代号和配方见表1。根据ISO 37—2017,制备哑铃2型的试样。每个试样在实验前都需要经过10次循环拉伸来消除Mullins效应,每种情况下的实验重复至少4次,试样拉伸的速率为300 mm·min－1并且将获得数据的平均值作为最终实验结果。

表1 4种不同含量炭黑填充硫化橡胶的配方和代号Table 1 Formulas and codes of four kinds of carbon black filled vulcanized rubber

1.2 实验结果及讨论

实验的拉伸结果截取到150%的应变范围,150%的应变范围完全可以覆盖绝大多数橡胶部件的变形情况。图1绘制了表1中C20,C40,C60和C0共4种橡胶的不同温度下名义应力和名义应变的关系曲线,温度分别为293,313,333,353,363和383 K。从图1可以看出,橡胶材料在一定变形范围内(150%应变)的超弹性行为具有明显的温度相关性,对于炭黑填充的橡胶胶料C20,C40和C60,随着温度的增加,应力-应变曲线整体先下降,在超过某一临界温度后,随温度的进一步升高而整体升高。也就是说,随着温度升高,橡胶试件首先变软,超过某一临界温度后,随着温度的升高而变硬。即填充橡胶的整体模量随着温度先下降后上升。而对于未填充的天然橡胶,即C0,其应力-应变曲线随着温度的升高而上升,并且没有转折的临界温度。

图1 4种类型橡胶在不同温度下的单轴拉伸应力-应变曲线Fig.1 Uniaxial tensile stress-strain curves of four types of rubber compounds at different temperatures

图2给出了在0.3,0.6,0.9,1.2共4种特定应变下,橡胶试件的应力-温度关系图。从图2看出,对于C20,C40和C60 3种不同类型的炭黑填充胶料,它们在恒定应变下应力的大小随温度升高先降低再增加。填充橡胶会先随温度的升高而变软,而当温度升至某一特定温度后,胶料又会随着温度的升高而逐渐变硬,即胶料的整体模量增加。且不同的炭黑填充质量分数的橡胶转折温度是不同的,可以看出炭黑填充量对橡胶力学特性的影响也很大。而对于未填充炭黑的橡胶C0,其在恒定应变下的应力随着温度的升高几乎接近线性地增加。这与图1结论一致。

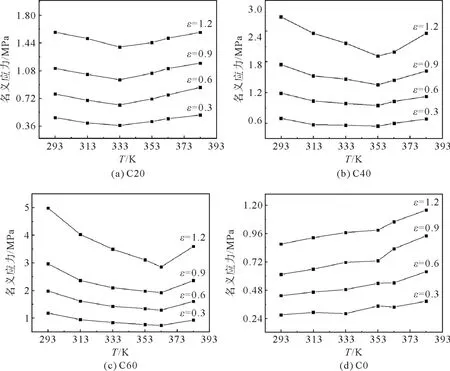
图2 4种类型的橡胶样品在不同恒定应变下的应力-温度曲线Fig.2 Stress-temperature curves at different constant strains for four types of rubber specimens

形成上述现象的原因为填充炭黑后橡胶材料各组分分子间整体有3种作用力:炭黑粒子吸附作用性形成的刚性键,橡胶分子链段的构象熵,还有各组分之间的相互作用力。在添加上炭黑粒子后,橡胶分子链吸附到炭黑上形成刚性键,这等效于增加了橡胶材料的分子链段数。在温度比较低时对刚性键和构象熵的影响不大,主要是分子间相互作用力起作用;但是温度比较高时分子比较活跃而构象熵增大,同时形成的刚性键也会增多。以上两种联合作用表现为填充橡胶先变软后变硬的现象。而填充炭黑越多橡胶形成的刚性键越多,越不容易受温度的影响,所以不同填充比橡胶的临界温度也不同。对于未填充的橡胶,其内部的主要作用力为分子链构象熵,而分子链间作用力很微弱,随着温度的升高构象熵增加,在宏观力学上表现为随温度升高橡胶整体刚度呈增加的趋势。

2 橡胶超弹性力学行为温度相关性的理论表征

2.1 改进八链模型

一些应变能函数可以引入修正项的方式来改善其某些方面的性能,如式(1)所示

式(1)中:W0为需要加入的修正项。

对血管这种超弹性材料进行研究时,发现指数函数修正项可以很好地描述其超弹性力学行为的非线性特征,从而起到很好的修正作用[9-10]。由于血管和橡胶具有类似的超弹性特性,所以参考血管超弹性模型来修正现有橡胶超弹性模型是可行的。有相关文献已证明指数应变能密度函数具有较高的捕获超弹性材料非线性力学特征的能力[11-12]。同时指数函数很容易满足热力学第二定律要求的应变能密度函数的正定性[13]。DARIJANI等[14]通过考虑多项式、幂律、对数和指数形式的数学函数的线性组合,提出了16种应变能密度函数。结果表明,与其他函数相比,包含指数项的应变能密度函数即使参数很少也可以精确地拟合可压缩材料和尤其是不可压缩材料的试验数据。

因此,对于本研究的橡胶超弹性材料引入如下形式的修正项:

其中:

考虑到模型的简洁性需求,令k＝1,l＝0。

基函数W选用Arruda-Boyce八链模型,八链模型具有一些优势,可以在某种水平上体现填充橡胶力学行为大致的非线性特征,但是八链模型在小变形和较大变形阶段还存在明显误差,在其精确度上还有较大改进空间[8,15]。为了提高模型的精度,使模型能够具有预测性,实现数值计算和拟合过程更加稳定、便捷和准确的目的,基于八链模型并结合血管超弹性材料本构模型的优点,通过在八链模型中引入指数修正项,提出了一种新的改进的Arruda-Boyce模型(也可以称为改进的八链模型)。在修正项中引入了2个附加参数,即全局相互作用因子a和b。修正项的参数表征填充橡胶内部各组分之间的相互作用效果,即橡胶内部分子链和分子链,炭黑和分子链,炭黑和炭黑之间相互作用情况。基于应变能函数热力学定义和分子链构象熵的变化,得到改进的八链模型如式(4):

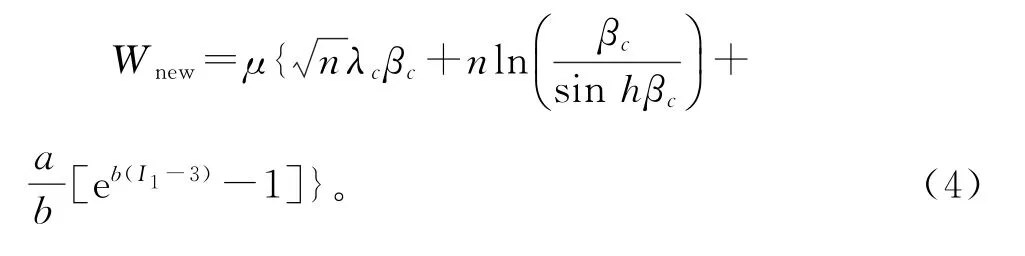
在该模型中有4个参数μ,n,a和b待确定。其中λc为链伸长。L－1(x)为逆Langevin函数。

结合TRELOAR和RIVLIN发表的理论[16-17],得到了改进的八链模型在单轴拉伸变形状态下的名义应力与拉伸响应的级数展开关系:

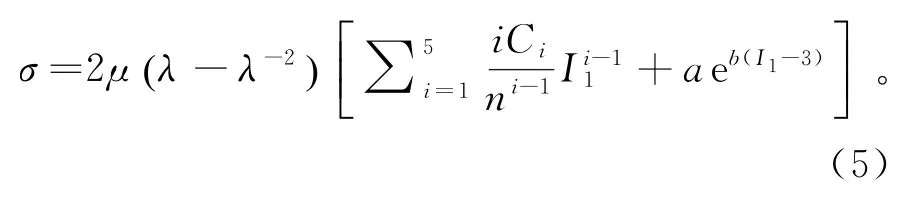
2.2 改进八链模型对橡胶温度相关性表征能力的评估

该模型对常温下橡胶不同变形状态的超弹性力学行为的表征能力以及在有限元中的应用情况已经得到验证[15]。采用改进的八链模型对不同温度下橡胶的超弹性进行表征,来对其理论表征能力进行评估。根据改进八链模型的表达式和实验结果,采用Levenburg-Marquardt非线性最小二乘法对不同温度下橡胶材料的应力-应变曲线进行拟合[18]。结果如图3所示,依次给出了C20,C40,C60及C0的拟合结果与试验数据的作图。表2～表5给出了改进八链模型对各胶料在不同温度下的拟合参数及相关系数。从图3及表2～表5的相关系数可看出,拟合曲线与实验曲线吻合得较好,这说明改进八链模型可以较准确地表征不同炭黑含量填充橡胶在不同温度下的应力应变过程。

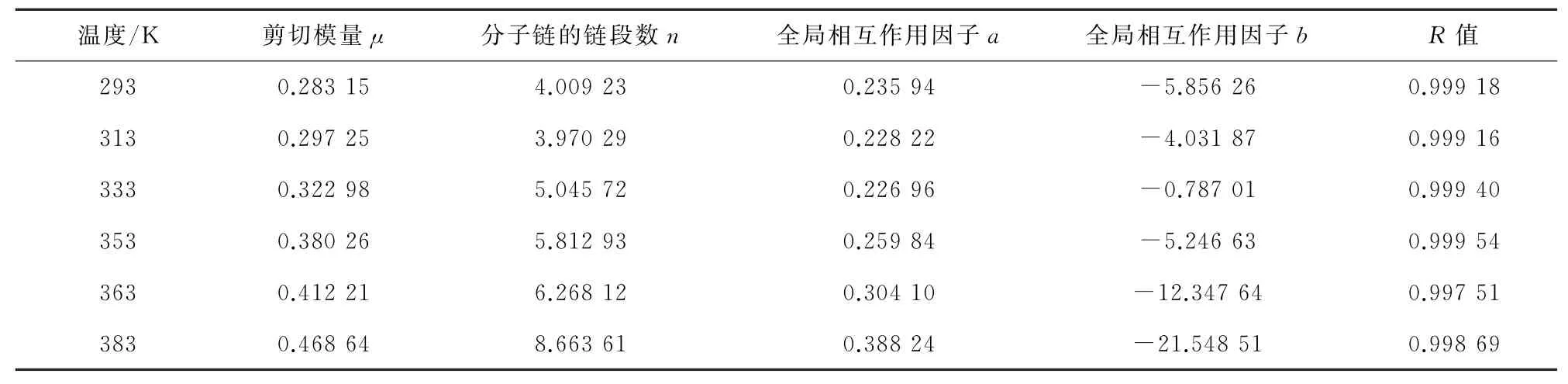
表5 橡胶C0在不同温度下的模型拟合参数Table 5 Model parameters of rubber C0 at different temperatures

图3 基于改进八链模型的4种橡胶在不同温度下应力-应变拟合曲线及相应的实验数据Fig.3 Stress-strain fitting curves and experimental data of four types of rubber compounds at different temperatures based on the improved eight-chain model

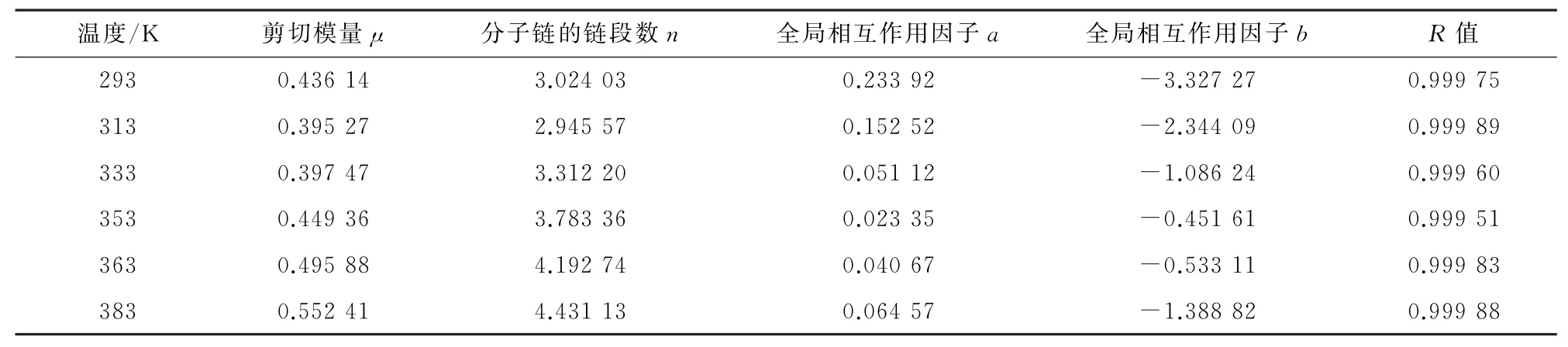
表2 橡胶C20在不同温度下的模型拟合参数Table 2 Model parameters of rubber C20 at different temperatures

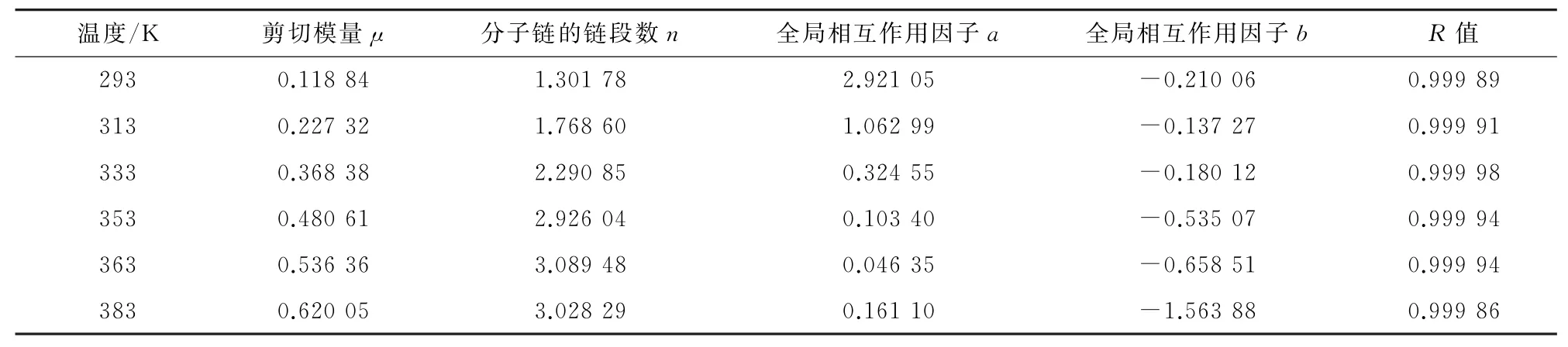
表3 橡胶C40在不同温度下的模型拟合参数Table 3 Model parameters of rubber C40 at different temperatures

表4 橡胶C60在不同温度下的模型拟合参数Table 4 Model parameters of rubber C60 at different temperatures

2.3 改进八链模型参数的温度相关性探索

目前,在改进八链模型中,没有显式的计及分析温度对橡胶在不同温度下表征结果的影响。因此,改进八链模型不能直接反映橡胶弹性与温度的依赖性。改进八链模型在不同温度下的拟合曲线与实验结果吻合得很好。此外,针对不同填充比的橡胶,还得到了在不同环境温度下的对应的模型材料参数。为了便于该模型的应用,有必要分析改进八链模型参数的温度相关性。因此,利用宏观唯象理论探讨了改进八链模型中材料参数与温度的关系。

将如表2～表5所示的参数和温度之间的关系用图4～7来表示。从图4～7可以看出,随着温度的升高,改进八链模型的4个参数呈现出不同的趋势。根据图形的特征和参数的物理意义分析变化趋势,可以得出以下结论:

1)根据Arruda-Boyce的八链理论,八链模型中的第2个参数n表示分子链中的链段数,是与温度无关的常数,但实际上n是与温度相关的[2,19-20]。从图4～7看出,随着温度的升高,n的确也近似按二次函数的形式变化。并且针对不同填充比的橡胶,n的值随温度也是大致呈增加趋势,说明温度越高胶料在拉伸过程中其内部链段之间断裂重组的形势也越发剧烈。

2)参数μ和参数n呈现大致相同的趋势,参数μ表示剪切模量,说明随着温度的增加,橡胶分子链的构象熵增加。虽然不同填充比橡胶增加的趋势不同,但大致呈现增加的趋势。

3)参数a和b随温度的变化情况较为复杂,可以理解为不同橡胶材料随温度的变化,内部相互作用不同。

4)根据图4～7中模型参数随温度的变化曲线,由于考虑到不同胶料性质的差异并且从拟合精确度出发,统一用二次函数关系表征改进八链模型参数的温度相关性规律是比较合适的,这样也可以保证模型的简洁性。

由此可见,可采用以下函数式来表示改进八链模型中材料参数与温度之间的定量关系:

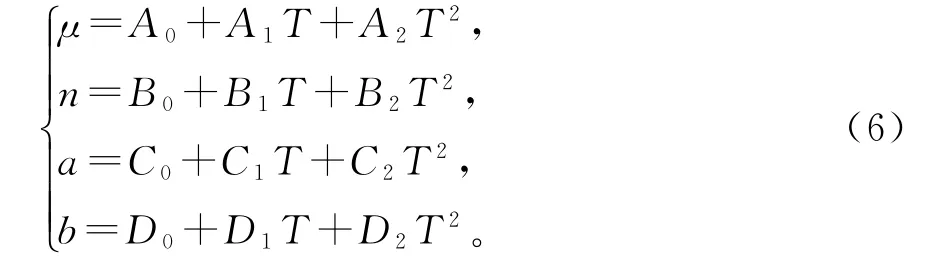
其中A0、A1、A2,B0、B1、B2,C0、C1、C2和D0、D1、D2为改进八链模型的温度相关特征表征参数,需要通过改进八链模型的参数拟合得到。对于某一种炭黑填充量的橡胶在不同温度下的改进八链模型参数,使用非线性最小二乘法按式(6)进行拟合,可以得到某一种橡胶的改进八链模型参数的二次函数拟合曲线,如图4～图7所示。针对系数随温度变化的二次函数拟合相关系数如表6所示。从根据图4～图7以及表6所提供的相关系数,可以看出二次函数的数值拟合结果与实验数据的材料参数基本吻合,因此使用二次函数数值拟合完全可以满足实际应用的精度要求。

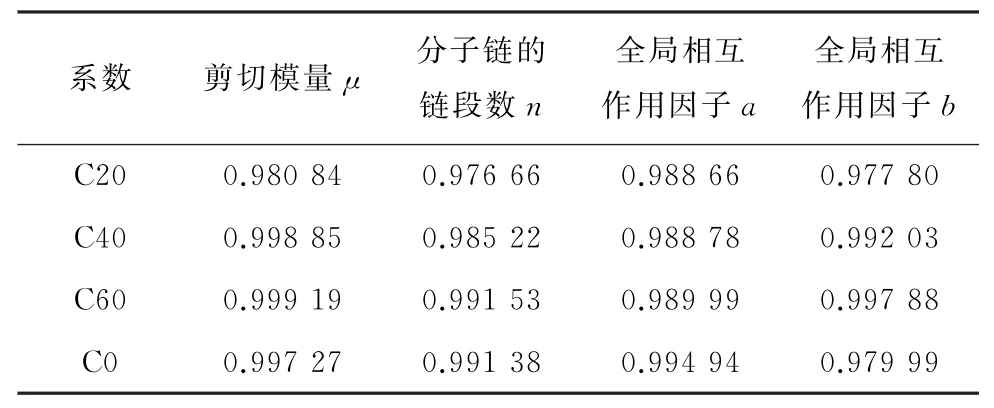
表6 4种橡胶改进八链模型参数的二次函数拟合相关系数Table 6 Quadratic function fitting correlation coefficients of parameters of the improved eight-chain model for four kinds of rubber

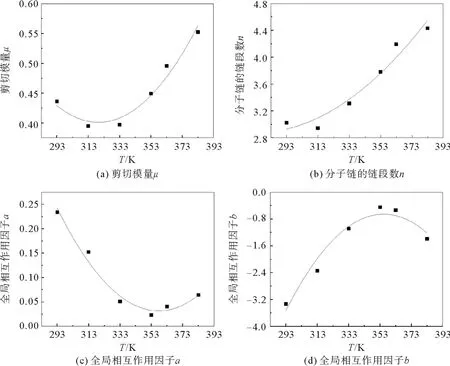
图4 橡胶C20的改进八链模型参数随温度的变化曲线及其相对应的二次函数拟合曲线Fig.4 Temperature-dependence curves of the improved eight-chain model parameters of rubber C20 and the corresponding fitting curves with quadratic function

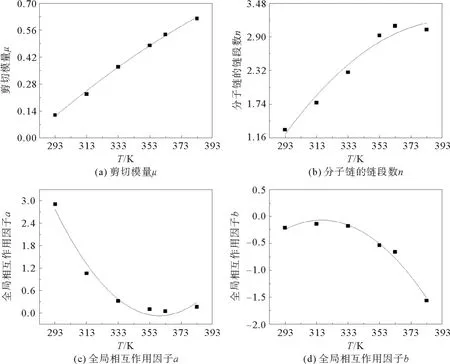
图5 橡胶C40的改进八链模型参数随温度的变化曲线及其相对应的二次函数拟合曲线Fig.5 Temperature-dependence curves of the improved eight-chain model parameters of rubber C40 and the corresponding fitting curves with quadratic function

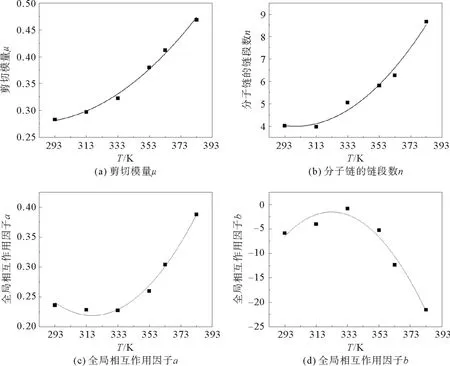
图7 橡胶C0的改进八链模型参数随温度的变化曲线及其相对应的二次函数拟合曲线Fig.7 Temperature-dependence curves of the improved eight-chain model parameters of rubber C0 and the corresponding fitting curves with quadratic function

图6 橡胶C60的改进八链模型参数随温度的变化曲线及其相对应的二次函数拟合曲线Fig.6 Temperature-dependence curves of the improved eight-chain model parameters of rubber C60 and the corresponding fitting curves with quadratic function