基于改进三支决策-TOPSIS方法的空战威胁评估
2022-12-30李天淳叶军吕康
李天淳,叶军,2,吕康
(1.南昌工程学院 信息工程学院,江西 南昌 330099;2.江西省水信息协同感知与智能处理重点实验室(南昌工程学院),江西 南昌 330000)
在空战领域中,由于科技手段不断发展,战场情况越加复杂,各平台的机动性和作战能力不断提升,所需要处理的数据量也在不断加大,对如何准确快速处理空战态势提出了新要求。空战威胁评估是一个典型的多属性决策问题,目前,诸多学者对此进行了研究[1-4],均可以有效实现空战威胁评估,但也存在一些问题:灰色关联度、层次分析法和模糊理论存在较大主观因素的影响;神经网络需要大量先验知识,因其推理速度较慢而难以满足空战实战要求;文献[1-4]中的方法可以对空战目标整体进行排序,但是在目标较多的情况下,给出所有排序却不加以分类,不利于作战资源的优化配置以及决策者的直观认知。
粗糙集理论[5]是一种处理不确定性数据工具,其无需先验知识可直接处理数据,客观性强,广泛应用于多属性决策领域[6-8]。粗糙集的拓展模型三支决策理论[9]由于融合了贝叶斯决策理论,具有容错性好、鲁棒性强等特点[10-12],因此在多属性决策领域取得了较好的应用效果。例如,文献[13-14]利用三支决策思想,结合TOPSIS方法,提出一种人力资源和水资源承载力的评估方法;文献[15]给出了一种乐观、悲观多粒度的直觉模糊三支决策定义,并应用到弹道导弹目标识别问题中;文献[16]在信息不全、资源有限的情况下,利用三支决策模型权衡了资源与效益。针对三支决策方法中条件概率确定的主观性问题,许多学者提出了改进方法,例如,Liang等[17]将TOPSIS法引入了三支决策理论,以各目标与正负理想解欧式距离求得的贴近度来计算条件概率。但TOPSIS法不能有效区分正负理想解中垂线上的多个目标,且容易造成逆序情况出现[18]。针对其不足,文献[19]引入了VIKOR法,提出了一种多目标威胁评估方法。但VIKOR法在信息有限的条件下进行评价可能会丢失部分信息,并且其没有考虑同类指标的互补性[20]。此外,这些改进方法只是把决策对象分为正域、边界域和负域3个域,无法对同一个域内对象进行排序。但在实际应用中,正域中可能会包含大量的决策目标,在某些情况下需要对域内这些目标排序,例如,在空中目标威胁领域,有多架敌机被划分为正域,即必要打击目标,则需要确定优先打击顺序;又如在通信领域,若有通信链路节点中断,多个节点都被划分为正域,同样需要确定正域中这些节点的优先抢修顺序,而单靠三支决策理论难以做到。
针对上述方法的不足,笔者拟引入概率优势粗糙集[21]的概念,建立基于改进三支决策-TOPSIS方法的空战威胁评估方法。首先,将原始数据正向化处理后,通过各目标间原始数据的相互优势对比从而求得概率优势度,并以此来对三支决策中的条件概率进行估计,提高其准确性,从而使得区域划分结果更加准确;其次,为充分考虑不同决策者的心理状态,通过设置不同的概率优势关系中的可信度进行灵活决策;然后,对正域内各目标进行TOPSIS方法排序;最后,通过一个空中威胁评估的实例来说明本文方法的有效性。笔者提出的三支决策与TOPSIS组合方法,不仅可以得到各目标属性以及需要对其采取的策略,且对正域内各目标都能有精确的排序,决策内涵丰富,清晰明了。
1 基本知识
1.1 粗糙集基本知识
在粗糙集理论中,知识通常采用信息系统的形式来表达,是用有序的四元数组来描述的。
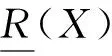
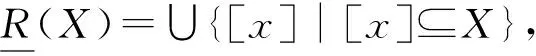
(1)

(2)
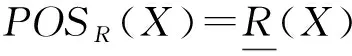
根据定义1可知,在经典粗糙集中对于上下近似集的划分过于严格,完全属于某个集合的等价类才能构成正域,完全不属于某个集合的等价类才能构成负域。因此,经典粗糙集在容错性方面存在不足。为此,研究者提出了概率粗糙集[24-26]和三支决策粗糙集等扩展模型[27]。
1.2 三支决策基本知识

(3)

1)P表示将一个属于X的对象x划分到正域:若R(aP|[x]R)≤R(aB|[x]R)且R(aP|[x]R)≤R(aN|[x]R)同时成立,则选择x∈POS(X)。
2)B表示将一个属于X的对象x划分到边界域:若R(aB|[x]R)≤R(aP|[x]R)且R(aB|[x]R)≤R(aN|[x]R)同时成立,则选择x∈BND(X)。
3)N表示将一个属于X的对象x划分到负域:若R(aN|[x]R)≤R(aP|[x]R)且R(aN|[x]R)≤R(aB|[x]R)同时成立,则选择x∈NEG(X)。

(4)
(5)
式中,阈值(α,β)满足0≤β<α≤1。由此可以得到简化的决策规则P1、B1和N1:
P1:如果Pr(X|[x]R)≥α,则x∈POS(X),
(6)
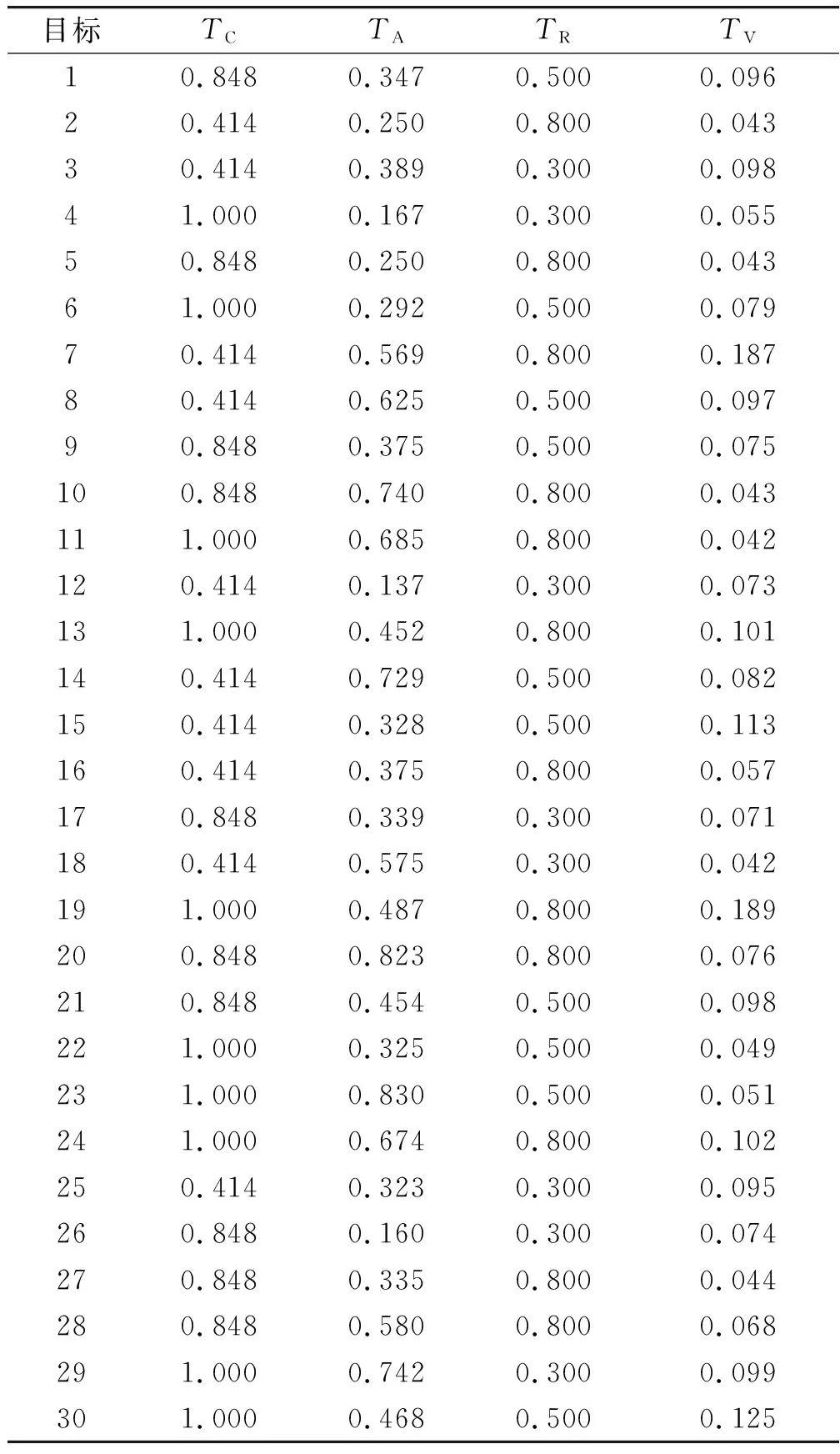
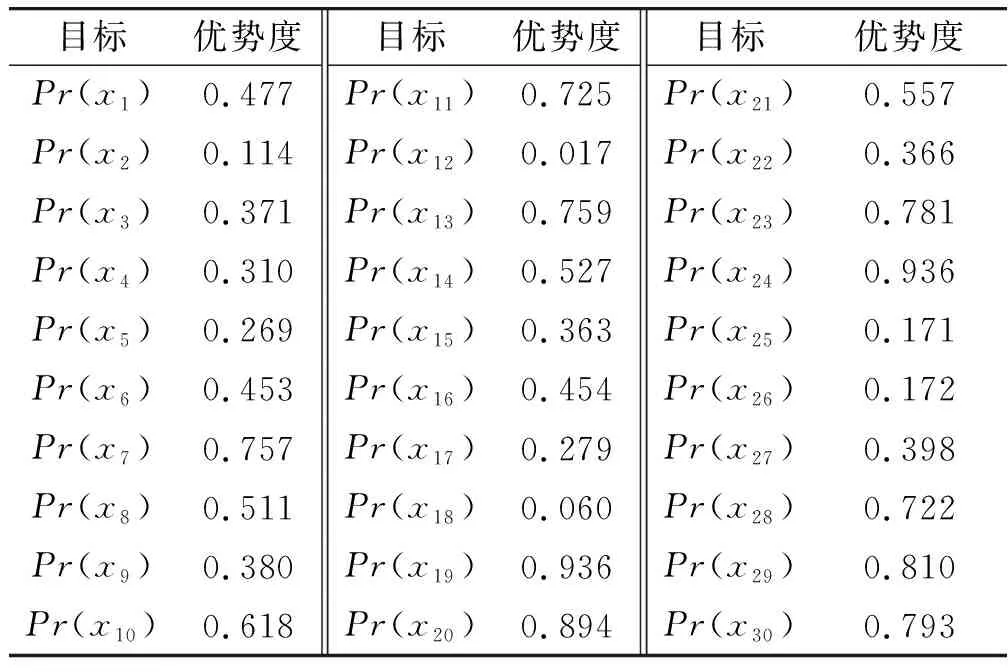
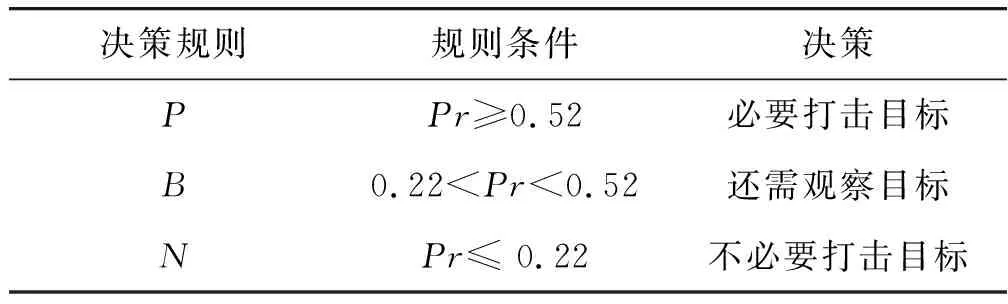
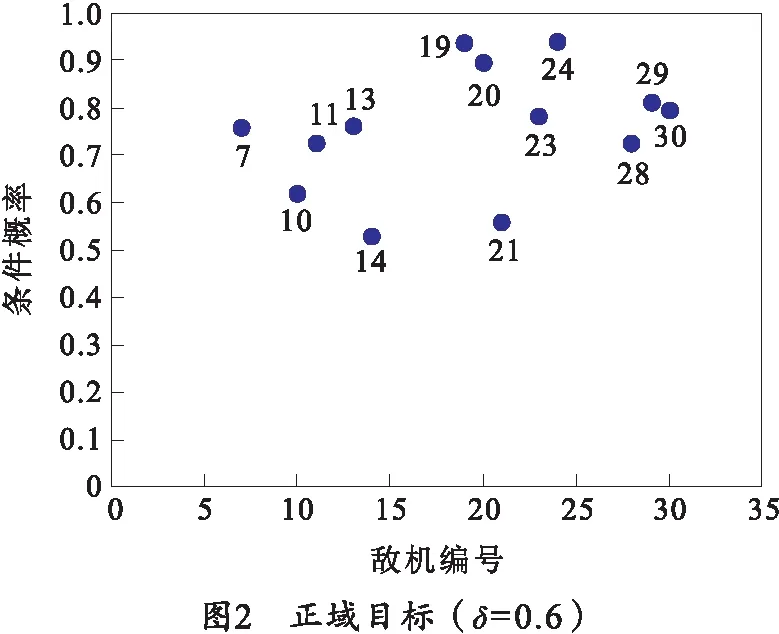
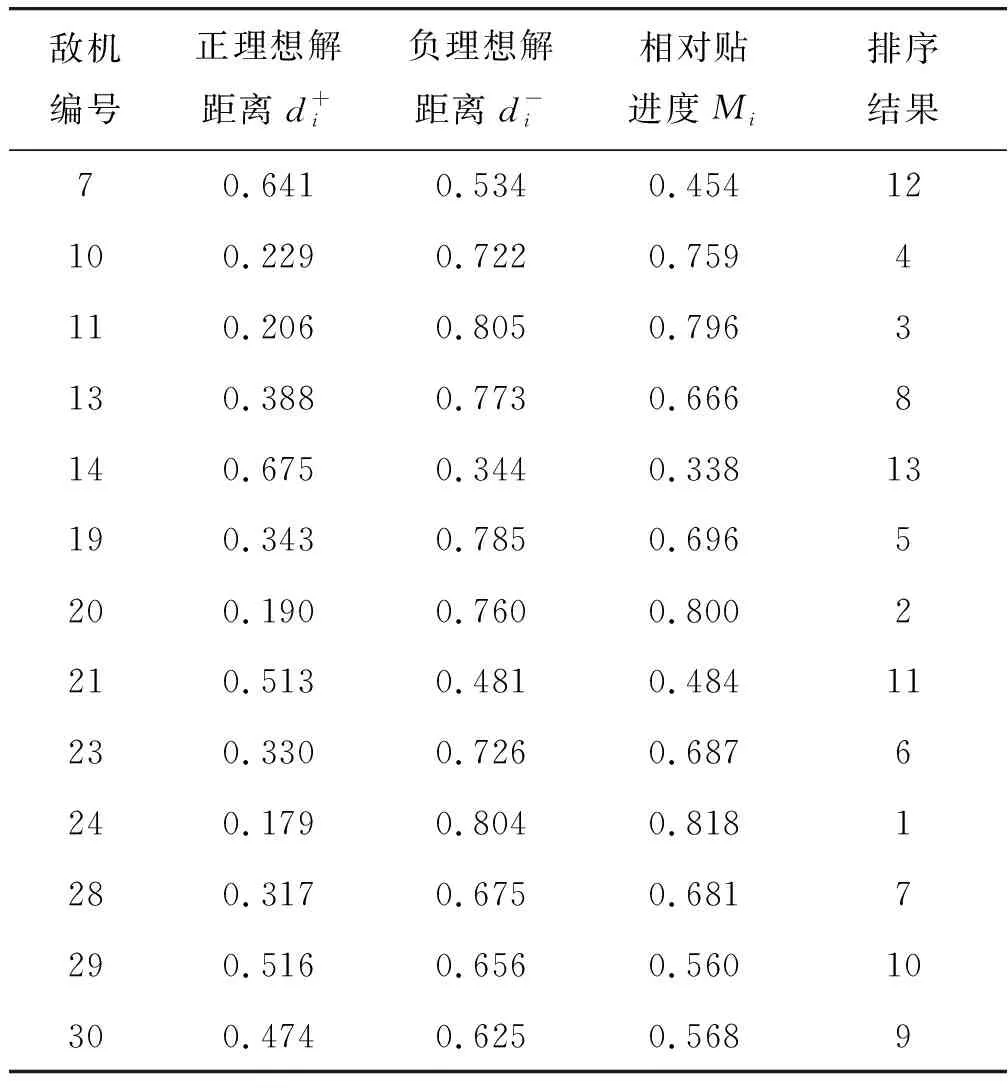
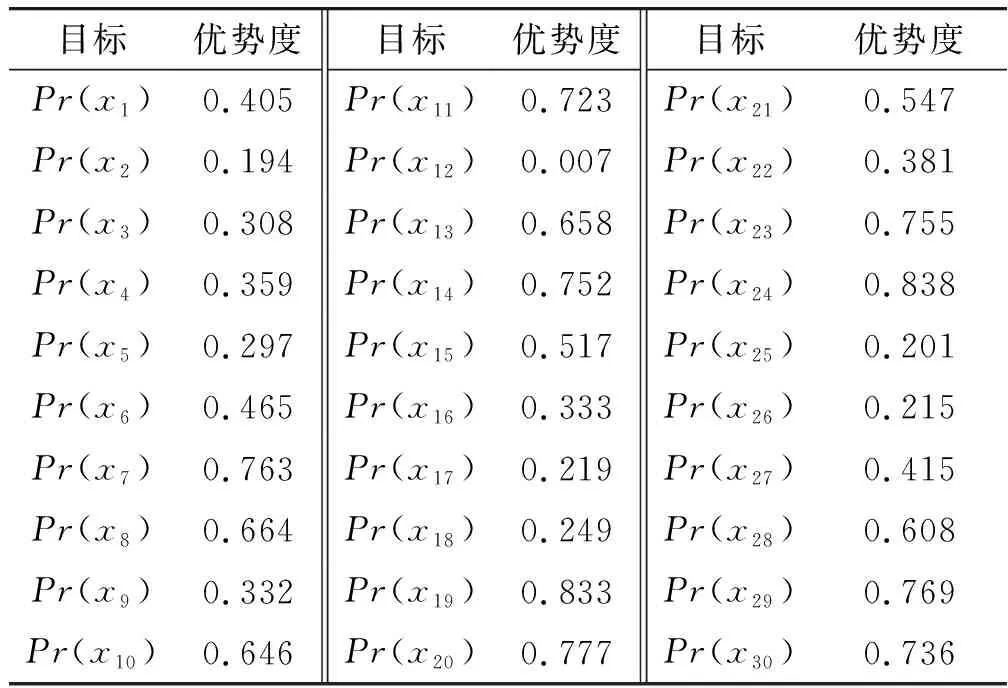
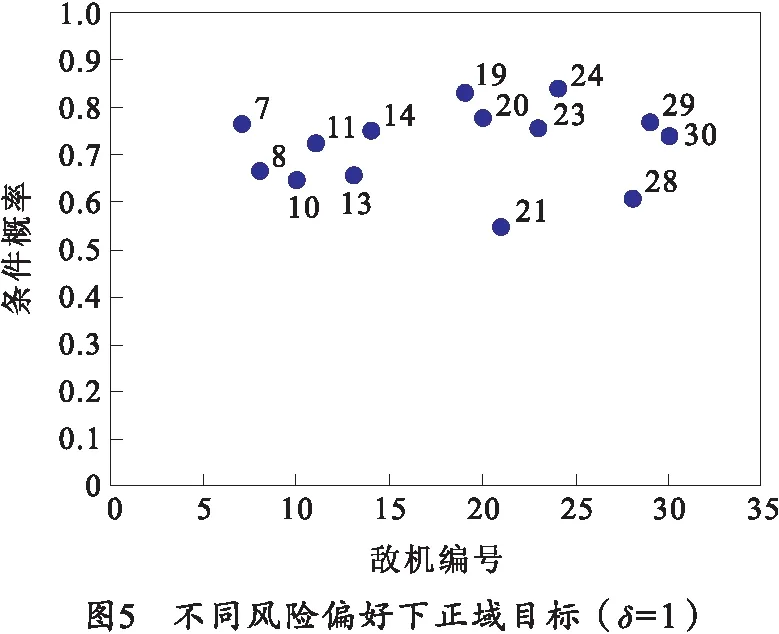
B1:如果β (7) N1:如果Pr(X|[x]R)≤β,则x∈NEG(X). (8) 2.1.1 目前常用方法及缺陷 2.1.2 改进的条件概率求解方法 步骤1分两步计算判断矩阵。首先计算对象在条件属性a下的二值判断,设S=(U,A,V,f)为一个四元信息系统,对∀xi,xj∈U,a∈A,对象xi与xj在条件属性a下的二值判断,由式(9)确定: (9) 判断矩阵为 (10) 式中,|B|为条件属性的个数。 步骤2计算概率优势矩阵。在四元信息系统S=(U,A,V,f)中,S在B下的概率优势关系为 (11) (12) 式中,0-1二值矩阵M与δ-概率优势关系一一对应。 步骤3划分概率优势类。在四元信息系统S=(U,A,V,f)中,给定可信度δ,[xi]B表示对象xi关于条件属性集B的δ-概率优势类,由式(13)确定: (13) 当δ=0.5时,只要半数为“优”即可判定为“优”,划分为风险型概率优势关系;而δ=1.0时,即:全数为“优”才能判定为“优”,划分为保守型概率优势关系。 (14) 将所求概率优势矩阵计算算数平均数即可得到各对象间的概率优势度,即: (15) TOPSIS法[33],又名逼近理想解排序法,其核心思想为在归一化后的原始数据矩阵中,找出有限个目标中的正理想解与负理想解,并计算各目标与正理想解和负理想解的欧几里得距离,以逼近正理想解而远离负理想解的目标作为最优目标,从而进行排序。该方法可以有效解决三支决策中只能划分区域却不能精确排序的缺点,可以为正域内必要打击目标提供合理的打击顺序,有利于火力资源的配置,具体步骤如下。 步骤1构造规范化评价矩阵。假设所有候选对象所组成论域U,共有m个,分别用u1,u2,…,um来表示;所有的评价指标即为条件属性A,共有n个,用a1,a2,…,an来表示。用xij表示某对象ui在对应的评价指标aj下的属性值,i∈M,j∈N,M={1,2,…,m}为论域U的下标集,N={1,2,…,n}为评价指标的下标集。 对于效益型指标,其值越大越优: (16) 式中,xmax,j和xmin,j分别表示第j列的最大值和最小值。 对于成本型指标,其值越小越优: (17) 由式(16)、(17)得到规范化评价指标矩阵: (18) 步骤2各对象贴近度计算。首先确定各项指标的最优解A+和最劣解A-: (19) (20) 步骤3计算最优解和最劣解。各方案与最优解、最劣解的加权正负欧式距离计算公式分别为 (21) (22) 步骤4计算相对贴近度。各方案与正理想解的相对贴近度为 (23) 显然,贴近度越大则代表该目标距离最优解越近,因此最终评估结果应按照相对贴近度Mi由大到小来对域内各目标威胁程度从高到低排序。 参考文献[34],从敌我空战态势和目标空战能力两方面建立空中威胁评价指标体系,如图1所示。目标空战能力中的机动性、火力和探测目标能力等7个评估指标的具体量化数值,笔者引用了文献[34]的数值。敌我空战态势中的角度威胁TA、速度威胁TV和距离威胁TR这3个评估指标的量化数值,按照文献[35]的量化公式进行量化。量化过程中各指标体系中的参数说明如表1所示,更为详细的解释说明参考文献[35]。 表1 火控雷达搜集空战态势参数说明 假设在某一时刻有30架敌机与我方遭遇空战,目标敌机都在我方火控雷达跟踪范围之内,监测到敌机类型有3种,分别为F-16C、F-5E、F-15E。我机的速度为320 m/s,导弹最大射程为60 km,雷达最大跟踪距离为120 km。限于篇幅,笔者不给出详细的空战态势表,直接给出在3.1节指标体系下,量化后得到的空战威胁指数表,如表2所示,并进行仿真。 表2 空战威胁指数表 根据2.1.2节提出的改进的条件概率求解方法,按照步骤1~4进行计算。参考文献[21],选取可信度δ=0.6,计算其概率优势度,计算得到的结果如表3所示。 表3 概率优势度 对必要打击目标、不需要打击目标作决策时造成的损失函数值进行设定。 对于必要打击目标采取了火力打击,极大限度的降低了我方受到的安全威胁,其损失函数λpp=0.05为最小,但由于战场的不确定性,其取值应大于0;对于必要打击目标若不采取火力打击,会让我方遭受到敌机巨大的威胁,其损失函数λNP=0.95,为最大值。但在实际情况中,我方也存在一定的防空防御能力,所以其取值应下沉,略小于1。 对不需要打击的目标采取了火力打击,可能会浪费火力资源,从而使威胁度较高的敌方目标对己方构成安全隐患,其威胁度应排在第2,λPN=0.8;对不需要打击的目标不采取火力打击是一种正确且节省火力资源的决策,但由于战场的不确定性和硬件的通信侦察能力所限,若敌机空战态势搜集不准确,某机威胁度本应很高却错判,也会对我方构成一定的威胁,其损失函数λNN=0.1符合常理。 对于两种打击目标都采取按兵不动的策略,通过空战态势进一步观察,其损失函数应介于其余4个损失值之间。最后得到的损失函数值如表4所示。 表4 损失函数值设定 损失值在战斗过程不断进行中,随着敌我双方态势的变化会一直改变,笔者仅针对某一特定时刻的空战态势进行实验仿真。 根据表4的损失函数值求出阈值α和β。由式(4)、(5)计算得到的阈值为α=0.52,β=0.22。根据得到的阈值和式(6)~(8),可以得到三支决策的规则,如表5所示。 表5 决策规则表 按照表5决策规则进行划分,划分结果如图2所示。 划分到正域,表明必要打击的目标有{x7、x10、x11、x13、x14、x19、x20、x21、x23、x24、x28、x29、x30}。 同样,需要有待进一步观察的目标有{x1、x3、x4、x5、x6、x8、x9、x15、x16、x17、x22、x27}。 不必要打击的目标有{x2、x12、x18、x25、x26}。 从上面的分类结果可知,得到的正域即必要打击的目标敌机有13架。对必要打击目标利用TOPSIS法进行排序,根据式(16)~(23)可得出计算结果,如表6所示。 表6 必要打击目标TOPSIS法排序结果 根据相对贴近度从大到小进行排序可得,这13个必要打击目标的最佳打击顺序为:x24>x20>x11>x10>x19>x23>x28>x13>x30>x29>x21>x7>x14。 从排序结果可以看出,最先打击x24目标,最后打击x14目标。这解决了三支决策理论中无法对正域(即必要打击目标)进行区分的局限性。 3.3.1 不同条件概率下优先打击目标的判定 采取改进后的条件概率计算方法,利用三支决策理论对30架敌机进行了3个域的划分,并由决策规则得出了必要打击目标。为了验证不同条件概率求解方式对于决策结果的影响,分别采取TOPSIS法和VIKOR计算各目标条件概率,依然按照表5的决策规则进行划分,并与本文方法得到的结果进行对比,计算结果如图3、4所示。 图3、4表明,在不同方法求出的条件概率下,所得必要打击目标各不相同,且差异较大,如方式不得当,势必会对空战决策的准确程度造成影响。笔者采取概率优势粗糙集的思想求解条件概率,基于原始数据驱动,无视指标量纲影响,在数据有微小波动或差异时具有一定的稳定性[36],不需要对指标权重进行设定[37-38],最大限度排除了主观性,且避免了TOPSIS法和VIKOR法求解条件概率时的相关弊端,其结果更加真实可靠。 3.3.2 不同风险偏好对于目标划分的影响 不同决策者在面对空战威胁评估时,对于风险偏好主观上是不同的,若决策者属于风险厌恶型,对于误差的容忍程度较小,则δ应选取较大值。选取δ=1,与3.2节δ=0.6时正域内元素进行比较,计算其概率优势度,计算结果如表7所示。 表7 概率优势度 依然按照表5中决策规则进行划分,划分结果如图5所示。 图5表明风险厌恶型决策者在设置可信度δ=1之后,正域内元素较δ=0.6时多了敌机x8。较高的可信度取值表明该决策者不愿承担过多风险,将更多的可能目标列入必要打击目标行列之中,其结果符合实际情况。 笔者提出的三支决策-TOPSIS空战威胁评估改进方法,利用了概率优势粗糙集来计算条件概率,由于其完全是基于原始数据,不需要人为设置权重,无视指标量纲影响,直接由两两比较得到结果,因此,新方法改善了原有求解条件概率方法存在主观性、局限性带来的不足,有效提升了条件概率准确性,由其划分得到的3个决策区域更加精确;同时,新方法融合了TOPSIS法,能够有效对区域内的决策目标按重要程度进行精确量化排序,决策结果更加直观;此外,该方法可以根据不同的决策者对于风险偏好,灵活选取可信度进行决策,结果动态化,更适用于实际情况。 当然,笔者的研究还存在不足:一是概率优势关系计算条件概率增加了计算工作量,提高了时间复杂度;二是对一些域内决策目标较少的决策信息系统作用不明显。2 改进的三支决策-TOPSIS评估方法
2.1 目标条件概率的计算


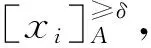
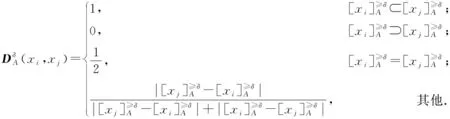
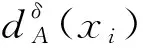
2.2 TOPSIS排序方法
3 空中目标威胁评估实例
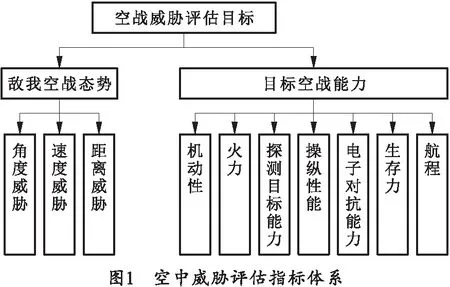
3.1 空中目标威胁评估指标体系的建立

3.2 算例仿真

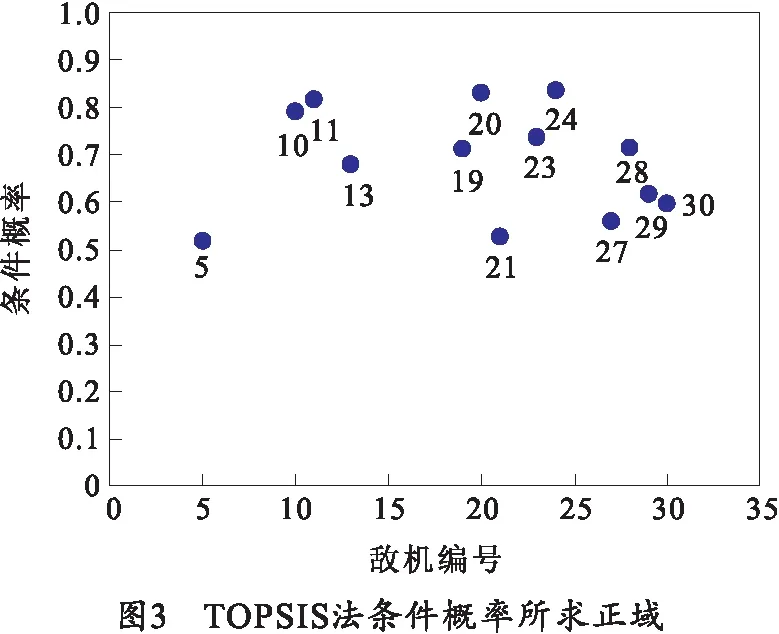
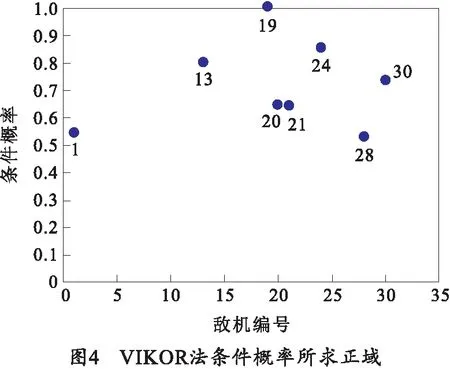
3.3 对比试验分析
4 结束语
