基于时间序列分析的高速公路小修工程量预测*
2022-12-29李许峰成高立罗雅琼史小丽
李许峰 成高立 罗雅琼 史小丽
(1.陕西高速机械化工程有限公司 西安 710038; 2.长安大学公路学院 西安 710064)
在公路养护市场化改革的过程中,养护预算编制的准确性和及时性是科学制定养护投资计划的基础。对公路养护资金测算进行有针对性地定量化研究,对实现养护费用的科学化、规范化管理具有较大的理论和现实意义。目前高速公路日常养护费用估算主要是根据养护预算定额计算各单项资产养护活动的费用总和确定的,这种估价方法需要预先确定各养护活动的工程量,再分别乘以其单价,汇总后得出总价。
目前国内对高速公路养护工程量的预测主要是通过分析影响养护费用的因素,建立养护费用或工程量与影响因素的数学模型,影响因素的分析过程常采用定性分析法[1-5]或定量分析法[6-7],常用模型包括多元回归分析模型、BP神经网络、灰色系统理论模型。部分学者着眼于探索路面使用性能与公路养护造价之间的关联性[8],文献[9]用层次分析法对历年路面使用性能指数PQI重新标定,采用灰色模型GM(1,1)预测短期PQI值,得出路面使用性能指数下降程度(100-PQI)与单位里程小修工程量呈线性关系。文献[10]建立路面状况指数与破损率之间的关系,并拟合工程量,对坑槽类破损效果较好。文献[11-12]采用灰色理论GM(1,1)模型预测高速公路养护成本;文献[13]使用时间序列分析的ARMA(1,1)模型对养管资金做出预测。
由于高速公路小修范围宽广、细目众多,现阶段研究更多聚焦于具有显著影响因素的小修细目(如路面小修细目),或者直接以日常养护费用这一总体性指标作为分析对象;前者使小修预算在编制过程中出现部分细目工程量无据可依的状况,后者太过笼统,不够精细化。事实上,有些细目其小修工程量并不受具体因素的影响,而是在运营过程中自然衰减呈现出随机性的变化特征;本文以此类小修细目为研究对象,对这些随时间变化的小修工程量引用python中的statsmodels库采用ARIMA模型进行时间序列分析,试图探寻此类小修细目工程量的变化规律。
1 小修工程量变化特征分析
某高速公路双向路基长度256.618 km,路面面积3 740 827.23 m2,桥梁双幅长度25 355 m,桥涵长31 457 m,波形梁钢护栏总长536 m。现有2004-2021年期间每年平均日交通量(AADT)、标准轴载当量轴次(ESAL)、重车交通量(HT)、重车比例(HR)、特大桥比例、交通事故次数和各养护细目小修工程量数据。
对于高速公路小修工程量的逐年变化,首先会考虑是否与交通条件有关,在此借助SPSS软件运用双变量相关性分析方法研究小修工程量的影响因素。相关性分析要求数据服从正态分布,对于不满足正态分布的数据取对数,取对数之后再进行相关性分析。以波形梁钢护拦板更换(二波)小修细目为例,对工程量与通车年限(OA)、AADT、ESAL、HT、HR进行皮尔逊相关性检验(皮尔逊系数为2个变量之间的协方差和标准差的商)。表1为相关性检验结果。

表1 相关性检验
由相关性检验表第一行可知,工程量与通车年限、年平均日交通量、标准轴载当量轴次、重车交通量、重车比例均无显著相关关系,即波形梁钢护拦板更换(二波)工程量的变化与项目记录交通条件无关。
归纳发现,标志标线的维修养护、伸缩缝维修、路肩与边坡的防护与清理、排水设施新建与养护、护栏零部件更换等小修细目并无具体的影响因素。对于这些细目养护工程量的预测,不能依赖因变量与自变量的关系建立回归模型,因此将目光放在时间序列分析上,研究工程量随时间的变化规律。
2 时间序列模型
时间序列分析通常用于对某一指标按一定顺序排列而成的数列进行研究分析,揭示数据本身蕴含的内在规律,进行短期预测。常用的时间序列模型有自回归模型(AR模型)、移动平均模型(MA模型)、自回归移动平均模型(ARMA模型)和自回归综合移动平均模型(ARIMA模型)。ARMA模型是前2种模型的组合,其三者原始时间序列均为平稳序列,ARIMA模型将非平稳序列转化为平稳序列后再进行剩余建模步骤。平稳序列即时间序列的均值和方差不发生明显变化。本文实例中无具体影响因素的小修细目工程量时间序列经平稳性检验后为非平稳序列,因此选用ARIMA(p,d,q)模型建立工程量与时间的关系。
ARIMA(p,d,q)模型是一种时间序列建模方法,其建模的基本思想是对非平稳的时间序列用d次差分(时间序列在t时刻与(t-1)时刻的差值)使其成为平稳序列,再用ARMA(p,q)模型对该平稳序列建模,之后经反变换得到原序列。式(1)为ARIME(p,d,q)的一般表达式。
yt=ø1yt-1+ø2yt-2+…+øpyt-p+
ut-θ1ut-1-θ2ut-2-…-θqut-q
(1)
式中:ø1,ø2,…,øp为自回归系数;θ1,θ2,…,θq为移动平均系数;{u}为误差白噪声,服从均值为0、方差为σ2的正态分布;{y}为原始时间序列差分后的平稳序列。
3 分析步骤
3.1 数据处理
将历年小修工程量按等间隔的时间先后顺序组成时间序列,对于缺少数据的情况,采用插值法或借助移动趋势线补齐。当预测高速公路某年的小修工程量时,截取该年度以前的小修工程量作为时间序列。
3.2 平稳性检验
平稳性即要求经由样本时间序列得到的拟合曲线在未来的一段时间内仍能顺着现有的形态“惯性”地延续下去,且序列的均值和方差不发生明显变化。对时间序列进行平稳性检验的目的是根据其平稳性建立与其相适应的时间序列模型。ADF检验即判断含有高阶序列自相关的序列是否存在单位根:如果序列平稳,就不存在单位根;否则,就会存在单位根。所以,ADF检验的H0假设是存在单位根,如果得到的显著性检验统计量Test Statistic小于置信度(10%,5%,1%)的临界值Critical Values,则对应有(90%,95%,99%)的把握来拒绝原假设,即序列平稳。
3.3 数据的纯随机性检验(白噪声检验)
当经过检验确定是平稳序列之后的数据并非都能值得建立模型,只有符合动态规律性,即数据之间存在一定的相依性,历史数据对未来的发展有一定的影响才值得去建立模型并做出预测。纯随机性检验就是检验数据是否值得建立模型的一项重要步骤。在进行纯随机检验之前,先引入纯随机序列,纯随机序列是指序列值彼此之间没有任何相依性,过去的数据行为对未来的发展完全没有影响。
从统计学角度来看,当时间序列为纯随机序列时,则表示该序列没有任何分析的价值。Python白噪声检验返回值lb_pvalue为基于卡方分布的p统计量,当p值小于0.05时表明序列为非白噪声序列。
3.4 模型定阶
p、d、q是ARIME(p,d,q)模型的3个关键参数;d为差分次数,可由时间序列经平稳性检验和纯随机性检验后确定;p、q为阶数,即当前时间节点的值与前p、q个历史值相关,阶数的确定需根据自相关图(图1)和偏自相关图(图2)判断。
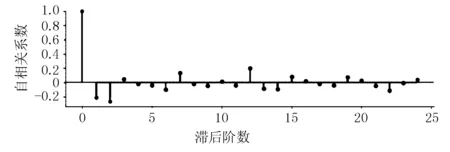
图1 自相关图
自相关函数(autocorrelation function,ACF)反映了t时刻和(t-k)时刻小修工程量yt、yt-k的相关性;k为滞后阶数,即当前时刻的值与前k个时间点的值有关。自相关图显示沿x轴的滞后阶数及y轴上的自相关系数(-1~1之间)。自相关系数实际上反映的不仅是yt、yt-k两者的相关性,还有yt-k+1、yt-k+2、…、yt-1对yt-k的间接影响。
偏自相关函数(partial autocorrelation function,PACF)是剔除中间(k-1)个变量的间接影响后,yt-k与yt的直接相关性。长条状渲染为95%的置信区间。
通过函数的自相关图和偏自相关图,可以确定出该模型的阶数,然后进行参数估计及显著性检验。表2为ARIMA(p,d,q)模型阶数确定表。

表2 ARIMA(p,d,q)阶数确定表
图1表示自相关图2阶截尾,图2表示偏自相关图2阶拖尾。若原始序列是平稳序列,模型则为MA(2);若序列是经d次差分后的平稳序列,模型则为ARIMA(d,2)。
4 工程实例
为了检验ARIMA模型预测方法的有效性,对依托工程高速公路2021年的小修工程量进行预测,并与实际值对比检验。以更换护栏螺丝、维修收水口(C25混凝土)、波形梁钢护拦板更换(二波)3个养护细目为例,表3为各年度小修细目工程量汇总表。
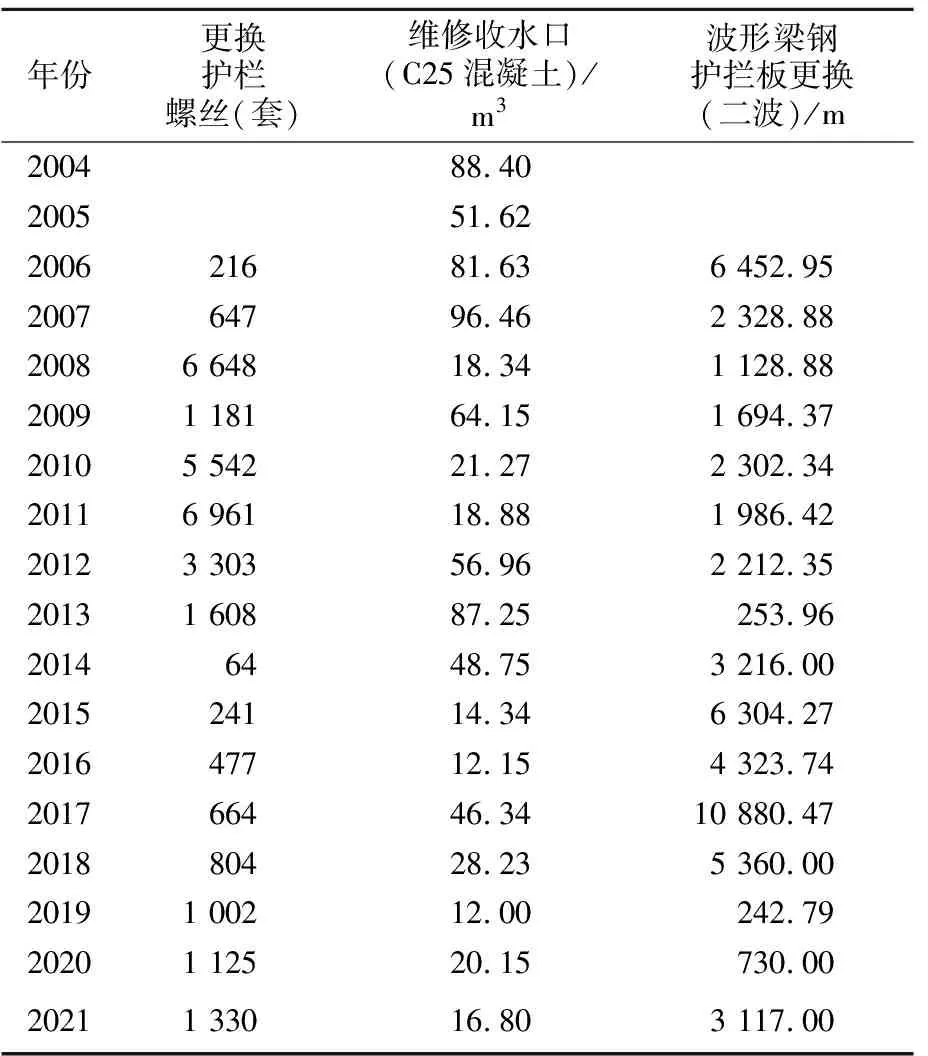
表3 小修工程量汇总表
当预测2021年的小修工程量时,取2020年及以前的数据作为时间序列。表4、表5为小修细目工程量时间序列平稳性检验和白噪声检验结果。

表4 时间序列平稳性检验结果表

表5 时间序列白噪声检验结果表
确定差分阶数d后,根据d阶差分序列的自相关图和偏自相关图,确定p、q值。表6为更换护栏螺丝、维修收水口(C25混凝土)、波形梁钢护栏板更换(二波)小修工程量模型系数表,表7为小修工程量预测值与实际值对比结果。

表6 模型系数表
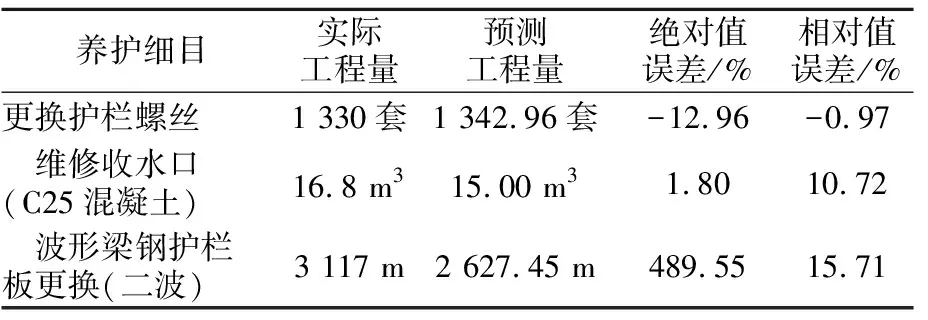
表7 预测值与实际值对比表
由于误差项是不确定的,所以没有具体的函数表达式,statsmodels库可直接得到预测值。
由表7可知,预测值与实际值的绝对差异较小,表明用时间序列模型进行预测的有效性;相对误差受到基数大小的影响,可作为辅助指标对预测结果进行判定。
5 结语
小修工程量的合理确定对日常养护预算编制具有十分重要的作用。通过对某高速公路的小修工程量数据分析,得出以下结论。
1)需采用定量化分析方法研究确定各小修细目是否具有影响因素。
2)当小修细目不具有显著的影响因素时,采用时间序列分析法预测小修工程量是一种可靠的方法。
3)不同养护细目需分别建立时间序列模型,且其模型不是一成不变的;因此需要及时更新积累的年度数据,用新数据加入后反映的趋势来预测未来年度的变化情况。
4)养护过程中数据的积累非常关键,从数据中挖掘出信息并用于决策,才能体现用数据进行养护管理的理念。
