基于共生搜索的生物地理学优化算法

朱晓雯，范成礼，卢盈齐，齐 铖，李 威

(空军工程大学，西安 710051)

0 引 言

由于精确算法在寻找复杂问题全局最优解中的表现不佳，近几十年来，各种模拟自然界现象的元启发式算法被不断提出，如粒子群算法、遗传算法、人工蜂群算法、蚁群算法等。

生物地理学优化[1](Biogeography-Based Optimization，BBO)算法是美国学者Simon于2008年首次提出的一种启发式算法。Simon证明，相较于常见的GA，PSO，ACO等算法而言，其对候选解具有良好的挖掘能力和全局搜索能力，因而受到了众多国内外学者的关注。不同算法在求解全局最优问题中都体现出不同的优势，但是由于“没有免费的午餐”，没有哪一种算法在任何方面都表现良好，因而当前算法的改进点都集中在提升求解精度和效率，并使其尽可能优于其他相关算法。

和其他算法相比，原始BBO算法也存在一些较明显的问题：迁移过程中对较优解的直接复制，种群的多样性不高；候选解受适应度值高的个别解强烈吸引，迭代后期出现多个解相近或是超级个体现象；算法早熟收敛等。因而学者专家也不断对BBO算法进行不同程度的改进。在BBO算法的优化方面，通常可分为以下几类：基于迁移和突变操作的优化[2-3]；与其他智能算法或精确算法杂交[4-6]；建立多种群或局部拓扑的BBO[7-8]。

与其他智能算法或精确算法杂交是优化算法的有效手段。本文引入共生生物搜索算法对原始BBO算法进行优化。共生生物搜索(Symbiotic Organisms Search，SOS)算法是Cheng等[9]于2014年提出的一种新型启发式算法。该算法模拟了生物体在生态系统中生存和繁殖所采取的共生互动策略，具有较强的鲁棒性和寻优能力。

为解决原始BBO算法存在的问题，更好地平衡算法的集约化和多样化搜索能力，本文汲取BBO算法和SOS算法的共性特点和互补优势，对BBO算法中的迁移和变异操作进行改进，提出基于共生搜索的生物地理学优化算法。SOS算法与BBO算法都受进化理论的启发而产生，理论上具有同源性，两种算法都不需要特定参数；BBO算法的优势在于不同栖息地之间的信息共享，SOS算法中生物共享优势协同进化的功能可以较好地促进BBO算法发挥特点。

反导WTA问题是经典的复杂全局优化问题，多种启发式算法被应用于求解该类问题。罗锐涵等[10]对BBO算法增加了三维变异操作，对火力分配方案进行优化，增加了对于方案的全局搜索能力。本文以导弹突防过程中的武器目标分配为背景，进行仿真实例应用。实例中进一步表明，该优化算法相较于原始算法和其他相关算法，较好地平衡了全局搜索和局部搜索的能力，并且一定程度上有利于提升求解精度和效率。

1 原始的生物地理学优化算法

BBO算法模拟了自然界中物种在不同岛屿之间的迁移，岛屿在BBO算法中被称为“栖息地(Habitat)”，那些被认为适合物种居住的栖息地有着较高的栖息地适宜指数(Habitat Suitability Index，HSI)，与这个指数有关的因素有降雨、植被多样性等，这些因素被称为适宜性指数变量(Suitability Index Variables，SIVs)。SIV可以看作是栖息地的自变量，HSI可以看作为因变量。

BBO算法线性模型如图1所示。HSI高的栖息地物种数量多，迁入率低、迁出率高；HSI低的栖息地物种数量少，迁入率高，迁出率低。因而迁移率可以作为物种迁移的标准。

图1 BBO算法线性模型

BBO算法的迁移过程可以描述为

(1)

(2)

式中：μk为第k个栖息地的迁出率；λk为第k个栖息地的迁入率；E为最大迁出率；I为最大迁入率；k为第k个栖息地当前的物种数量；n为最大物种数量。迁入率和迁出率都取决于栖息地的物种数量。

此外，BBO算法中，为了实现种群的多样性，种群的内部会进行变异操作，概率为

(3)

式中：m(k)为第k个栖息地的变异率；mmax为用户定义的最大变异修改概率；Pk为当前物种数量概率；Pmax=max(Pi)。

2 共生生物搜索算法

SOS算法体现了生态系统中的不同生物体互利共生、协同进化的特点，主要由三个阶段构成：

(1)互利阶段

(4)

(5)

(6)

式中：Xi与Xj为两个候选解；rand为(0，1)之间的随机数；由于两个生物之间相互作用时总存在一方获取收益大，另一方获取收益小的情况，因而获利因子BF1和BF2∈{1，2}；MV为生物之间的互利向量，体现了Xi与Xj之间的关系特征。

(2)共栖阶段

(7)

式中：随机选择的候选解Xj与Xi进行互动，生物Xi从与Xj的互动中获益，而Xj未受到影响；(Xbest-Xj)体现了Xj帮助Xi提升至最优解的最大程度。

(3)寄生阶段

在此阶段中，Xi为寄生变量，Xj为生态系统中随机选择的寄生变量的宿主，Xi试图取代生态系统中的Xj。通过对Xi和Xj两种生物体的适应度进行评估，如果Xi比Xj有更好的适应性，则会替代Xj，否则Xj将保留。

3 改进的生物地理学优化算法

3.1 改进思路

BBO算法存在一些固有的问题：(1)初始种群的生成具有随机性；(2)迁移机制中在栖息地的选择中使用轮盘赌的方式，存在很大的随机性，且耗时长、计算复杂度高；(3)迁移操作中通过对已选择的SIV特征进行直接复制，导致在整个优化迭代的过程中对新解的勘探能力有限，容易被个别HSI很高的精英解强烈吸引，从而出现超级个体或过早收敛的情况；(4)突变操作对种群后半部分较差解进行变异，这个变异方向是随机的，无法保证向优质解方向变异，且对于新解的探索贡献不足。

针对以上问题，本文以BBO算法为主，引入SOS算法中的思想，对BBO算法的核心步骤：迁移操作和突变操作进行改进，提出SBBO算法。首先，对初始种群进行优化；其次，在迁移机制中，对栖息地选择进行动态调整，引入余弦自适应框架，并与SOS算法中互利操作进行融合；突变操作中，引入SOS算法中的共栖操作对原始突变进行优化。仿真实例表明，SBBO算法有利于扩大种群多样性，同时可提高算法的求解精度和效率。

3.2 初始种群优化

由于初始种群的生成是随机且无向的，首先根据共生生物搜索算法中的互利操作，使初始种群进行初步优化，便于对优质解的探索:

Hi_new=Hi+rand×(Hbest-MV×BF1)

(8)

Hj_new=Hj+rand×(Hbest-MV×BF2)

(9)

(10)

式中：Hi_new和Hj_new为经过互利操作协同进化生成的新的栖息地；Hi与Hj为随机选取的栖息地；MV为两个栖息地之间的互利向量；BF1和BF2∈{1, 2}为获利因子。初始种群优化过程如图2所示。原始种群在可行域内生成的位置是无向且随机的，因而存在如图中Hj远离最优解的解。而互利操作可以使Hi与Hj以不同的程度向最优解靠近，从而使初始种群向最优解范围进化，进化程度由rand×(Hbest-MV×BF1或2)决定，这个程度是随机的，并不会降低初始种群的随机性。该优化操作有利于减小初始解生成的随机无向性，并加速对最优解的寻找过程。

图2 初始种群优化

3.3 迁移算子改进

3.3.1 基于动态选择的迁移算子

在BBO算法对迁出的栖息地选择中，主要采取轮盘赌的方式，这种选择概率都是随机的，无法根据不同迭代阶段进行相应的变化，容易造成种群的多样性不高、算法过早局部收敛的问题。

因而本文设置了栖息地动态选择策略，即在不同的阶段中，进行迁入迁出操作时，规定不同的选择压力。在早期, 缩小选择压力，使HSI值较低但可能含有优秀SIV因素的栖息地能够更多地参与到迁移过程中，保持种群的多样性；在后期, 适当增加选择压力，使种群能够较快收敛，从而更加趋近最优解。本文提出以下选择概率：

(11)

(12)

式中：Pk为第k个解被选择进行迁出的概率；μk为当前栖息地的迁出率；n为种群数量；μi为任意第i个栖息地的迁出率；G为当前迭代次数；Gmax为最大迭代次数；a为选择压力因子；pdmax为选择压力因子的变化初始值；pdmin为选择压力因子的变化终值。

pdmax和pdmin为定常参数，为测试pdmax和pdmin对算法性能的影响，选择具有代表性的多峰不可分Ackley测试函数进行实验。表1和图3显示了不同取值的pdmax和pdmin对整体优化效果的影响。可以看出，pdmax和pdmin取值对算法整体寻优趋势有较大的影响，当pdmax=0.9，pdmin=0.1时, 优化效果最佳。其原因是在迭代前期收敛速度慢，后期收敛速度快，同时求解精度增加，符合压力选择的原则。

图3 式(11)～(12)实验结果

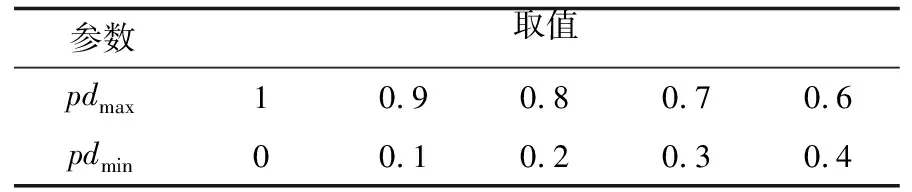
表1 pdmax和pdmin的取值

改进后, 动态栖息地选择公式前期收敛速度慢，有利于进行全局搜索；后期收敛速度快，有利于加强局部搜索，取得的结果也较优，并且较原始BBO算法的栖息地选择上有较大改善。

3.3.2 互利迁移算子

其他算法中针对迁移算子的改进如表2所示。

表2 其他算法中BBO迁移算子修改回顾

表2中，α，F为文中确定的随机参数；t为当前迭代次数；T为最大迭代次数；k为最大种群数；k1,k2,k3为原文中选取的栖息地。

综合以上迁移操作的修改来看，主要是通过将选择的迁入地进行修改或者是多个栖息地按照一定的比例进行迁入，然而迁入和迁出的栖息地在进化中并不是完全孤立的。在自然界中，两个不同的栖息地也可能因为迁入的物种而发生适应性的变化，从而使两者的适应性程度得到提升。受这一思想启发，本文引入SOS算法中的互利操作。如图4所示，针对第j维的栖息地，左侧是原始BBO算法的迁移过程，右侧是对选择的迁入地和迁出地进行互利进化，二者都吸收相互间的有利因素，通过互相学习和反馈，进行协同进化:

图4 迁移算子修改

Hi_migration=Hceil(rand×(MV×BF1-1))

(13)

Hk_migration=Hceil(rand×(MV×BF2-1)

(14)

(15)

式中：Hi和Hk为选择的迁入地和迁出地；MV为两个栖息地之间的互利向量，体现了两个栖息地之间的关系特征；BF1和BF2为获利因子，体现了两个栖息地协同进化时一方进化程度高、一方进化程度低的情况，因而BF1和BF2∈{1, 2}，而Hceil(rand×(MV×BF1或2-1))则反映了当前栖息地和最优栖息地之间的关系，进化过程表现了向最优栖息地进化的过程;Hi_migration和Hk_migration为迁移生成的新的栖息地。这种协同进化的过程避免了单一栖息地的直接迁移复制的缺点，使两个栖息地能够协同进化，有利于增强种群的多样性，并加速对最优解的寻找过程。

3.3.3 余弦自适应框架的优化迁移算子

为进一步提升BBO算法在不同阶段的搜索能力，在前期以互利迁移算子为主，后期以动态选择策略迁移算子为主。本文利用余弦自适应策略将互利迁移算子与动态选择迁移算子融合，提出改进的余弦动态自适应因子：

(16)

图5反映了余弦动态自适应因子的变化趋势，呈现震荡的动态变化规律以及总体下降收敛的趋势。当随机概率大于α时，采用基于动态选择策略优化的迁移算子进行修改；当随机概率小于α时，采用互利迁移算子对栖息地进行优化。

图5 迁移算子修改余弦动态自适应因子变化趋势

基于余弦自适应框架的迁移算子有以下优化性能：

(1)在迭代前期主要采用互利迁移进行修改，该算子被选择进行修改栖息地的概率很大，有利于维持种群的多样性，避免局部最优的出现。

(2)在后期运用动态选择策略迁移算子进行修改，这种动态选择策略较大程度结合了原始算法的特点，利于算法收敛。

(3)余弦动态自适应因子总体震荡变化的趋势避免了修改策略的单一性，同时也有利于对未知区域的探索，使栖息地中并不是特别优秀的个体有一定的生存概率，避免了全部被修改替代从而出现相近和重复的现象。

该迁移算子伪代码如下：Population为整个种群；rand为[0，1]中的随机数；n为种群数量；d为种群维度；pmodify为迁移修改率；lp为变量取值下界；up为变量取值上界。

改进的迁移算子伪代码(算法1)如图6所示。

Input: Population, n, d, λ, μ, α, pmodify, lp, up1 for i=1 to n do2 if rand > pmodify then3 continue4 for j=1 to d do5 if rand< λ then6 if rand<= α then7 Renovate habitati (SIVj) with equation(13)～(15) base on the restriction(lp, up)8 Else 9 Renovate habitati (SIVj) with equation(11)～(12) base on the restriction(lp, up)10 Else11 habitati(SIVj)=habitati(SIVj) Output: Population

3.4 共栖突变算子

原始BBO算法中的变异操作主要对HSI排序后较差的后一半解根据变异概率进行变异，但是这种变异是随机进行的，并不具有有向性，可能向好的方向变异，也可能向不好的方向变异，同时该过程对于提供优秀解的贡献较小。

为减小变异的随机性，引入SOS算法中的共栖思想，即针对后半部分的较差解，从前半部分较优解中随机选择对象进行互动，从而获利并增强自身适应性程度：

Hi_mutation=Hi+rand×(-1, 1)×(Hbest-Hk)

k=round(length(n/2)×rand)

s.t.i∈(n/2,n),k∈(0,n/2)

(17)

式中：Hi_mutation为当前变异操作后新生成的栖息地；Hi为选择的当前进行变异操作的栖息地；Hbest为当前迭代过程中的最优栖息地；Hk为随机选择的HSI前n/2中的一个栖息地。针对HSI排序较后的一半栖息地，通过向前变异，在HSI排序的前n/2个栖息地中随机选择共栖对象，通过与之互动从中获益，(Hbest-Hk)体现了Hk帮助Hi提升至最优解的最大程度，该变异过程如图7所示。

图7 突变算子修改

该突变算子伪代码如下：Population为整个种群；n为种群数量；d为种群维度；lp为变量取值下界；up为变量取值上界；Pk为突变概率。

改进的突变算子伪代码(算法2)如图8所示。

Input: Population, n, d, λ, μ, lp, up1 Use λk and μk to compute the probability Pk2 Use HSI to rank the population3 for i = n/2 to n do4 for j = 1 to d do5 if Pk > rand then6 Renovate habitati(SIVj)with equation(17)base on the restriction(lp, up) Output: Population

3.5 SBBO算法流程

SBBO算法流程图如图9所示，具体流程为

图9 SBBO算法流程图

Step 1: 设置相关算法参数，初始化种群。

Step 2: 计算每个栖息地的HSI值，并由优到劣进行排列。同时保留q个精英解。

Step 3：开始迭代。

Step 4：根据互利操作对初始解进行优化。

Step 5：根据算法1进行迁移操作。

Step 6：根据算法2进行突变操作。

Step 7：重新计算栖息地HSI并确保解可行性。

Step 8: 对栖息地重新排列，并将保存的q个精英解替换最差q个解。

Step 9: 判断是否达到最大迭代次数，如果是，则输出结果；如果不是，则返回Step 3。

4 实验与分析

为比较不同算法的优劣，选取了包含单峰、多峰、可分、不可分离函数的测试集，如表3所示。该测试集来源为文献[14]中的基准测试函数，包含2个单峰函数、2个多峰函数、2个可分离函数、2个不可分离函数。类别一栏中，U表示单峰函数，M表示多峰函数，S表示可分离函数，N表示不可分离函数。本文主要从以下两方面对算法进行仿真实验和数据分析：(1)SBBO算法与BBO算法及变体的优化性能进行对比分析；(2)不同维度下SBBO算法的优化性能分析。

表3 测试函数

4.1 与BBO算法及变体的优化性能对比

在8个测试函数中，分别对包括BBO和SBBO在内的5种BBO算法进行优化性能的实验。本实验随机生成100个30维种群，迭代200次，并独立运行30次，相关参数及取值如表4所示。

表4 参数设置

对比算法分别为BBOPSODE[15]，BBO，ANLGBBO[8]，DGBBO[16]，如表5所示。对比数据分别为独立运行30次后所求最优值的平均值与标准差，粗体表示不同算法中的最优结果。分析表5可得，相同的测试环境中，SBBO算法所得的结果要明显优于其他几种算法。

表5 不同BBO算法测试结果对比

针对单峰函数f1、f2、f5、f6而言，SBBO算法所得结果的均值与最小值都在几种算法中最优，并且相较于BBO算法，求解的精度有了明显提升。其中，f1函数中体现最为明显，SBBO算法所得的平均值约为原始算法的1/7。f1、f5为可分离函数；f2、f6为不可分离函数。在标准差中，可以发现f1、f2、f5、f6的标准差结果均优于其他几种算法。

针对多峰函数f3、f4、f7、f8而言，SBBO算法在f3、f4中的均值和最小值在几种算法中最优，而在f7、f8函数中得到的均值和最小值仅次于ANLGBBO算法。相较于BBO算法，SBBO算法求解精度也得到大幅度提升，其中f3函数得到的均值约为原始函数的1/2。f3、f7为可分离函数；f4、f8为不可分离函数。在标准差中，f3、f4、f7函数所得的标准差都最优，而f8函数的标准差仅次于BBOPSODE算法。

由于不可分离函数相对于可分离函数而言，其适应度值由不同变量之间组合得到；而多峰函数相对于单峰函数更为复杂，有多个极值点。因而不可分离函数与多峰函数相对更加贴近于工程实际问题。从以上算法结果分析可得，针对多峰函数，SBBO算法的优化均值结果和最小值在总多峰函数中占比为50%，标准差占比为75%；针对不可分离函数，SBBO算法的优化均值、最小值、标准差结果在总多峰函数中占比为75%。总体分析可得，相较于其他几种优化算法，SBBO算法在多峰函数和不可分离函数中总体表现良好。

图10展示了8个测试函数在不同算法中经过200次迭代后的变化趋势。分析可得，在f1、f2、f3、f4、f5、f7函数中，SBBO算法所得结果优于其他算法；在f6函数中，SBBO算法所得结果仅次于ANLGBBO算法，并且两者结果极为接近。从图10可以发现，SBBO算法在初期的迭代过程中求解精度与收敛速度有略次于其他算法的趋势，但在迭代后期，SBBO算法的收敛速度和求解精度都明显高于其他算法，符合本文算法提出的初衷。分析这种现象可得，该算法在前期收敛速度慢，增加了种群的多样性，对未知解空间进行更多探索，从而使算法在后期能够提升求解精度。同时，在迭代不同阶段采用不同的选择压力，使前期收敛速度慢，后期收敛速度快。

图10 不同BBO算法变化趋势

4.2 不同维度下BBO算法优化性能对比

表6随机选取了f1、f2、f4、f7函数在BBO算法与SBBO算法中不同维度下求解的结果，这4个函数分别为单峰可分离、单峰不可分离、多峰不可分离、多峰可分离函数。运行参数设置同4.1节，分别独立运行30次。

分析表6可得，相较于原始BBO算法，SBBO算法在高维函数的求解中，性能普遍得到提高。在对f1、f2函数的30/50/100维、f4函数的30/100维、f7函数的30/50维下的求解结果中，SBBO算法所求的均值、标准差、最小值的结果均最优。在f4函数的50维和f7函数的100维结果中，SBBO算法的标准差略高于原始BBO算法，稳定性表现略有不足。综合以上数据可得，在高维度下，SBBO算法在4种函数中表现均较为良好。

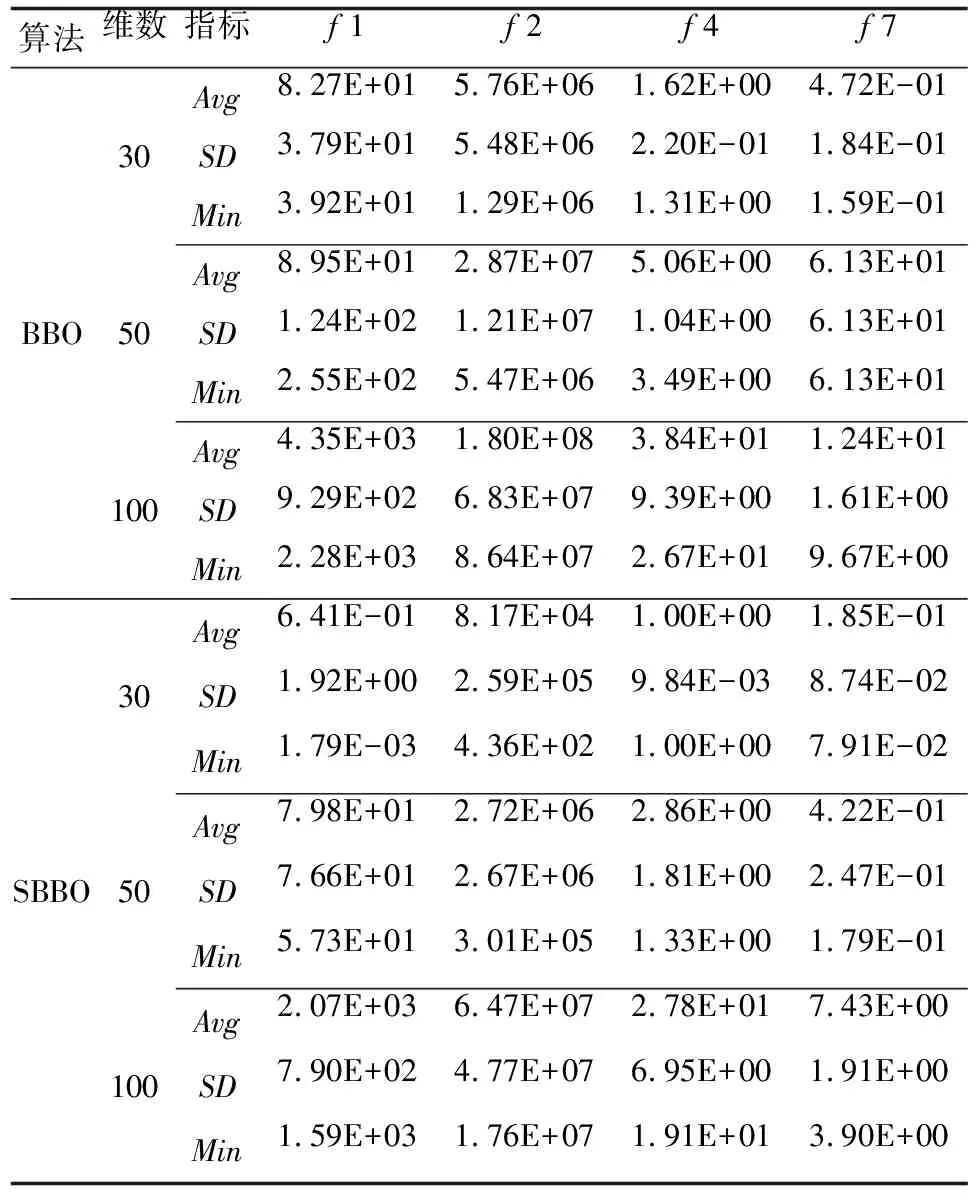
表6 不同维度算法测试结果对比

由于高维函数中，函数复杂度的数量级会相应地提升，通过不同函数在30/50/100维的情况下进行对比，所得结果验证了SBBO算法在求解高维问题中求解精度与效率的稳定性，与改进策略中对于新解的探索开发能力的提升有关。本文算法的优化进一步提升了算法的寻优能力。

4.3 SBBO算法与其他不同算法性能对比

针对PSO，GA，ACO三种算法与SBBO算法进行对比实验，测试函数与运行参数同4.1节，分别独立运行30次，粗体表示对比实验中的较优结果，如表7所示。

分析表7数据可得，在f1～f7测试函数中，SBBO算法在平均值、标准差与最小值几个方面所得结果均优于PSO，GA和ACO算法；在f8测试函数中，SBBO算法所得的标准差结果次于PSO, GA和ACO算法，而平均值和最小值优于其他几种算法。综合以上数据，可以得到, SBBO算法求解精度要显著优于其他几种算法。

表7 不同算法测试结果对比

4.4 SBBO算法复杂度分析

本文算法每一代复杂度主要由种群初始化、精英解保留、迁移操作、变异操作四部分组成。设种群规模为M，维度是N，则种群初始化时间复杂度为O(M)，精英解的保留过程时间复杂度为O(1)，迁移过程的时间复杂度为O(MN1)，变异过程时间复杂度为O(MN2)。在一个时间步骤中，总的实际复杂度最差为O(M)+O(1)+O(MN1)+O(MN2)=O(M+1+MN1+MN2)=O(MN), 与原始BBO算法的最差时间复杂度相差不大。

4.5 SBBO算法收敛速率分析

文献[17]中提出新的度量进化算法收敛速度的方法——平均收敛速度。具体操作过程为：针对最大化或者最小化问题，将进化算法看作一个迭代过程，首先构造一个初始解种群Φ0，然后生成一系列种群序列Φ1,Φ2,Φ3等，重复这个过程，并将找到的最佳解决方案存档。用f(Φt)表示种群Φt的最佳适应度值，因为其是随机变量，因而考虑其均值ft=E[f(Φt)]，令fopt表示最佳适应度值，则进化算法在t次迭代后的平均收敛速率为

(18)

若出现f0=fopt的情况，则设R(t|Φ0)=1。

根据以上平均收敛速率定义选取Sphere，SumPower，Griewank，Rosenbrock四种不同类型的测试函数，运行参数设置同4.1节，分别独立运行30次，可以得到如图11所示的平均收敛速率图像。

图11 SBBO算法收敛速率图

分析图11可得，在本文提到的单峰、多峰、可分离、不可分离函数中，随着迭代次数的增加，运用本文算法均可使目标函数收敛。

5 实例分析

反导过程中的武器目标分配(weapon target assignment, WTA)问题对于作战决策起着重要的作用，如何合理利用现有资源、分配已有兵力和武器单元来打击敌来袭目标，从而达到最优作战效果是WTA问题的主要内容。由于反导WTA是一个NP-hard问题，因而本文将SBBO算法应用于求解反导WTA问题。

5.1 反导WTA模型

反导WTA模型的目标是在最大化毁伤目标价值的基础上最小化作战代价。为简化模型、便于分析，将打击风险性作为作战代价函数，提出最大化费效比函数如下：

(19)

式中：Xij∈Z，i=1, 2, …,n,j=1, 2, …,m；maxE为最大化毁伤目标价值；minR为最小化作战代价；n为武器平台的数量；m为第j个来袭目标数量；Vj为第j批目标的威胁度，0≤Vj≤1；Pij为第i个武器平台被第j个目标毁伤的直接概率，0≤Pij≤1；Xij为第i个武器平台对第j个目标使用的火力数量，形成关系矩阵[Xij]m×n；Rij为第i个武器平台对第j个来袭目标进行打击的风险性。

该函数模型约束条件有：每种反导武器系统可以同时打击多个敌来袭目标，且多种武器系统可以打击同一敌来袭目标；每个来袭目标至少分配一个火力；每个武器平台配备多个火力，同一作战时间内每个武器平台对来袭目标分配的火力不能超过该武器平台的火力总数。

5.2 战局假设

为考察SBBO算法求解武器分配问题的寻优性能，给出以下实例：假设某次导弹突防过程中我方武器平台数量4，敌方目标数量4，对应火力单元数量为(8，10，8，10)，不同目标对于武器平台的威胁度分别为(0.58，0.67，0.78，0.48)。武器-目标分配参数如表8所示。参数设置为：种群100，突变率0.05，迭代300次。

表8 武器-目标分配参数

5.3 结果分析

表9为应用SBBO算法求解反导WTA问题得到的最终分配结构。

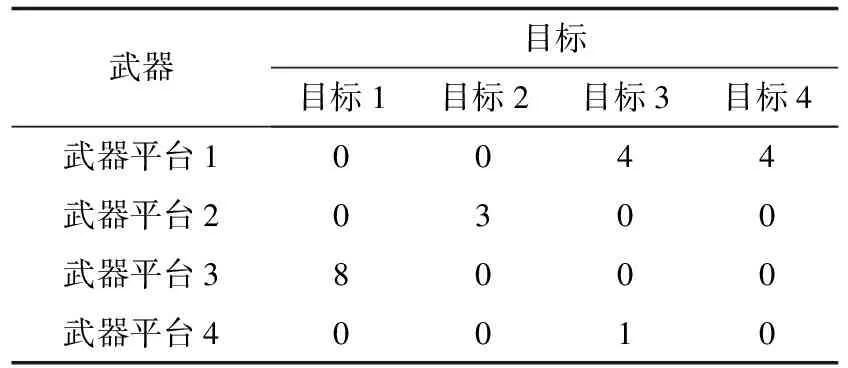
表9 武器-目标最终分配结构

图12为本文算法求解反导WTA问题的迭代趋势图，对比算法为原始BBO算法。可以看出，SBBO算法在前期收敛速度较慢，后期收敛速度加快且解的HSI值要更高，说明改进后的迁移和突变算子在前期增加了解的多样性，后期增加了解的求解精度，较原始BBO算法有更强的全局搜索能力和收敛速度。

图12 SBBO算法迭代趋势图

6 结 论

生物地理学的优化算法在解决全局优化问题中具有无需参数、编码简单、灵活的优点，但也存迁移机制中随机性强、耗时较长、计算复杂度高、特征直接复制, 突变机制中变异方向随机、对于新解的探索贡献不足的缺点。

本文提出的SBBO算法，对初始随机种群进行了优化，提出余弦自适应框架下的动态选择迁移和互利迁移优化算子；同时，提出共栖变异算子，对原始BBO算法进行优化，一定程度上解决了原始BBO算法存在的问题，更好地平衡了算法的集约化和多样化搜索能力。基准测试函数与仿真实例表明，该优化算法相较于原始算法和相关算法，较好地平衡了全局搜索和局部搜索的能力，并且有利于提升求解精度和效率，适应高维复杂问题的求解，有利于解决复杂工程问题。