任意时间收敛碰撞角约束制导律设计

刘远贺, 谢年好, 欧阳海, 黎克波*

(1.国防科技大学 空天科学学院，长沙 410072；2.空天任务智能规划与仿真湖南省重点实验室，长沙 410072)

0 引 言

对制导武器而言，制导系统的主要作用是根据弹目相对运动信息，给出合适的制导指令，使导弹精确命中目标。为了充分发挥导弹的作战效能，提高对目标的毁伤能力，在以最小脱靶量攻击目标的同时，希望其能以不同的落角或碰撞角实现对目标的全方位攻击[1-2]。如反舰导弹期望从近防武器系统防御薄弱的角度攻击战舰，如图1所示；钻地弹在攻击地下目标时，期望的攻击角度为垂直于地面；反坦克导弹希望以大落角对坦克顶部的薄弱装甲实施攻击等。

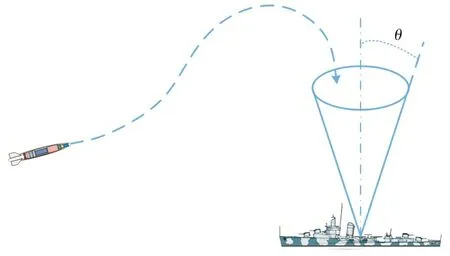
图1 碰撞角约束制导律示意图

碰撞角约束制导律(Impact Angle Constrained Gui-dance，IACG)最早由Kim等[3]于1973年提出，此后针对不同的作战场景和需求，并基于不同的控制理论，产生了不同类型的IACG。总的来说，IACG的设计方法主要有偏置比例导引、最优制导、滑模制导、先进几何制导等几类[4-6]。

为了实现碰撞角约束，可在纯比例导引律(Pure Proportion Navigation, PPN)的基础上加入偏置项，用以消除打击终点的落角或碰撞角误差。文献[7]基于类李雅普诺夫方法，提出一种具有碰撞角约束的修正比例导引律，不仅可以打击固定和慢速移动目标，对具有一定加速度的机动目标也具有良好的打击效果。文献[8]推导了具有角度约束的偏置比例导引律的闭合解，可以解析地确定所需的角度偏差，方便逆向推导以确定合适的拦截平面和导弹机动能力大小的初始条件。文献[9]提出一种有偏置项的反比例导引律，可用于拦截高速目标，并实现碰撞角控制。文献[10]针对半捷联末制导碰撞角约束问题，研究了圆弧比例导引和偏置比例导引两种制导律。文献[11]针对非机动目标，提出一种考虑导引头视场角和过载能力限制的碰撞角约束偏置比例导引律。文献[12]以高超声速滑翔飞行器末制导角度约束问题为背景，通过对PPN的性能分析，推导了碰撞角约束下的闭环非线性自适应制导律，但该制导律在初始阶段会带来较大的诱导阻力。文献[13]改进了该方法，在制导初始阶段设计了一种定向制导策略，提出一种复合制导律。文献[14]将该制导律进一步扩展到打击常速目标的情况，设计了一种两阶段比例导引律。文献[15]考虑外部扰动，又引入积分滑模控制方法和扩张状态观测器，设计了IACG。上述文献所涉及的多种制导律仍存在形式复杂、制导参数过多、物理涵义不明确等问题，当前导弹碰撞角约束制导律的设计与工程应用仍有很多可改进之处。

导弹制导问题本质上是制导误差的有限时间收敛问题。文献[16]基于施瓦茨不等式提出了非线性最优误差动力学方法，并提出一种基于最优误差动力学的IACG(OED-IACG)。文献[17]进一步提出一种具有导引头视场角约束的三维OED-IACG。文献[18-19]在此基础上引入飞行时间约束，设计了具有最优特性的时间角度控制制导律，并给出飞行时间包络。文献[20]发展了误差动力学方法，提出固定时间收敛的误差动力学方法，然后在此基础上设计了一种基于固定时间收敛的误差动力学的IACG，该方法可以使导弹的碰撞角误差在设定的固定时间内收敛到0，而此固定时间与初始相对运动状态无关。文献[21]基于固定时间收敛的误差动力学方法，引入导引头视场约束，设计了三维分布式多弹协同制导律，该制导律不包含切换逻辑，制导指令平滑且无奇异。

进一步针对制导律中涉及的有限时间收敛问题，文献[22]给出有限时间和固定时间稳定性的详细概念，有限时间和固定时间稳定的收敛时间上界一般与初始条件或控制参数相关，这对导弹的初始运动状态提出了要求。文献[23-24]通过时变调整函数预设收敛时间，并可以加入执行机构过载约束，甚至不需要系统的全局信息，即可实现固定时间或有限时间收敛的性能要求。虽然该方法可以通过合理选择参数得到期望的收敛时间，但预设性能的时变调整函数一般比较复杂。针对以上问题，文献[25]提出一个收敛时间可以任意设定的控制方法，该任意时间收敛方法具有结构简单、参数较少、物理意义明确的优点。

针对IACG设计问题，受文献[25]启发，结合文献[16]的研究思路，本文基于PPN和任意时间收敛控制方法，设计了任意时间收敛碰撞角约束制导律(Arbitrary Time Convergent IACG，ATC-IACG)，分析了其与OED-IACG的区别和联系，并选取不同制导参数，通过多种场景的仿真验证了所提制导律的有效性。

1 问题描述

1.1 导弹运动模型

在进行制导律设计前，不失一般性，给出如下假设：(1)导弹为理想质点模型，导弹动力学是理想过程，无执行机构时间延迟；(2)不考虑地球引力与地球自转角速度的影响；(3)导弹速度为常速，导弹加速度矢量垂直于导弹速度矢量，即不改变导弹速度大小；(4)目标静止。

弹目相对运动模型如图2所示。图中，oxy为惯性坐标系；M和T分别为导弹和目标；rm和rt分别为导弹和目标的位置矢量；vm为导弹运动速度矢量；r为弹目相对位置矢量；(er，eθ)为视线坐标系；(tm，nm)为导弹速度坐标系；q为视线角，φm为导弹速度倾角，θm为导弹前置角，均以er逆时针旋转为正。

图2 弹目相对运动模型

根据以上定义，导弹运动方程为

(1)

弹目相对运动方程为

(2)

式中：am为导弹加速度。

碰撞角约束的初始和终端约束条件为

(3)

式中：t0和tf分别为初始时刻和终端碰撞时刻；φmd为期望的终端碰撞角。

1.2 任意时间收敛方法

有限时间收敛方法的收敛时间上界由系统初始状态和参数决定；固定时间收敛的收敛时间上界与系统初始状态无关，但需要由参数决定；预设时间收敛方法的收敛时间上界可以通过时变调整函数预设，但时变调整函数形式复杂；任意时间收敛方法的收敛时间不仅与系统初始状态和参数无关，而且具有形式简单、收敛时间上界可以任意设定的优点。文献[25]提出一个收敛时间可以任意设定的控制方法，其状态方程具有如下形式：

(4)

式中：η∈R，且η≥1；tf为独立于任何系统参数和初始条件的收敛时间，可任意设定。式(4)的解析解为

x=ln[C(tf-t)η+1]

(5)

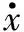
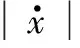
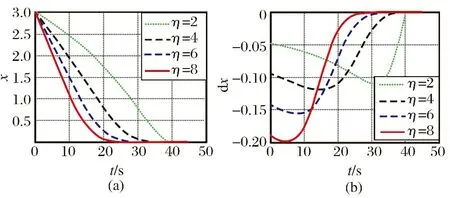
图3 参数η对式(4)的影响特性

2 任意时间收敛碰撞角约束制导律设计

对于静止目标，IACG通常采用比例导引加偏置项的形式[16]，即

am=aPPN+aIA

(6)

式中：aPPN为纯比例导引项；aIA为碰撞角约束项。在PPN导引下，终端碰撞角φmf同当前视线角q和速度倾角φm的关系为

(7)

应注意，PPN导引下的导弹，其速度前置角θm最终会收敛到0，也就是说, 视线角q和速度倾角φm最终会收敛到一致，即φmf=qf。

令期望的终端碰撞角为φfd，那么碰撞角误差可以定义为

εφ=φfd-φmf

(8)

对式(8)求导，并将式(2)、式(6)～(7)代入，经过整理，可得碰撞角误差动力学方程为

(9)

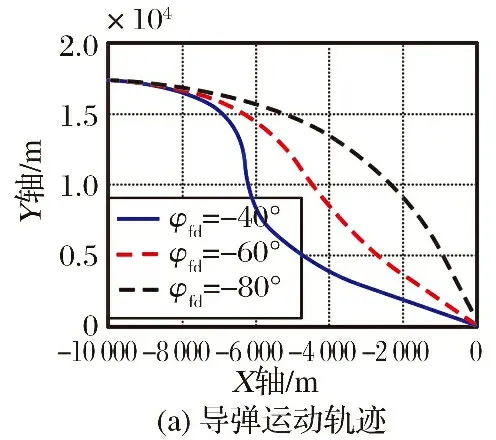
回顾任意时间收敛控制方法，即式(4)，可知当t

(10)

将式(10)代入式(9)，可得任意时间收敛的碰撞角约束项：

(11)

可知，当t>tf时，碰撞角误差已收敛到0，碰撞角约束项为0，即aIA=0。联立式(6)和式(11)，可得ATC-IACG为

(12)

式(12)所示的ATC-IACG收敛时间与系统的初始条件无关，且可任意设计。根据图4所示的方程收敛特性，为使过载均匀分布，一般选择收敛时间tf接近整个制导飞行时间。当收敛时间tf为总制导飞行时间，并把e-εφ在0处泰勒展开后取一阶近似，式(12)可以表示为

图4 收敛时间tf对式(4)的影响特性

(13)

式(13)即为文献[16]中的OED-IACG。由于总制导飞行时间未知，可以用剩余飞行时间的估计值tgo来替换(tf-t)项，即

(14)

式中：K为最优误差动力学的参数；tgo为PPN的剩余飞行时间估计，近似表示为

(15)

与其他制导律设计方法相比，OED-IACG可以在tgo时间内使误差收敛到0。此外，该制导律是基于非线性误差动力学理论推导的，有明确的性能指标，并且与基于线性化假设的弹道成型制导律结果一致。

3 制导律仿真验证

设导弹初始位置为[-10 000，17 321]m，初始速度为[500，0]m/s，即导弹平飞。目标位于坐标原点，即位置为[0，0]m，速度为[0，0]m/s。导弹最大过载设为amax=10g。

3.1 场景一：不同制导律对比

首先对比式(12)所示的ATC-IACG和式(14)所示的OED-IACG，选取终端碰撞角φfd=-60°，ATC-IACG的制导增益N=3，收敛时间tf=30 s，可调参数η=3，OED-IACG的制导增益N=3，参数K=3。

图5给出了ATC-IACG和OED-IACG的导弹运动轨迹、制导加速度、碰撞角误差和视线角变化曲线。仿真结果表明，两种制导律都实现了期望的终端碰撞角约束，但ATC-IACG的碰撞角误差能更快地收敛到0，视线角变化幅度较小。

图5 ATC-IACG和OED-IACG的仿真结果

不同制导律的导弹能量消耗如表1所示，其中速度增量是表征导弹能量消耗的一种方式，是对制导加速度的绝对值进行积分。由表1可知，ATC-IACG的能量消耗要少于OED-IACG。

表1 不同制导律的导弹能量消耗

3.2 场景二：不同收敛时间对比

选取收敛时间tf分别为30 s，35 s，40 s，碰撞角φfd=-60°，制导增益N=3，可调参数η=3。图6给出了不同收敛时间下的导弹运动轨迹、制导加速度、碰撞角误差和视线角变化曲线。

图6 不同收敛时间下的仿真结果

由图6(a)和图6(c)可知，在所设计制导律的作用下，实现了以期望收敛时间和终端碰撞角约束的攻击任务。由图6(b)可知，所设定的收敛时间越长，导弹制导加速度变化越平缓。由图6(c)和图6(d)可知，所设定收敛时间越短，碰撞角误差的收敛速度越快，导弹视线角变化幅度就越小。

收敛时间不同时的导弹能量消耗如表2所示。由表2可知，收敛时间越长，导弹能量消耗越多。这是因为设定的收敛时间越长，就会有越多的能量用于调整碰撞角。

表2 收敛时间不同时的导弹能量消耗

3.3 场景三：不同碰撞角对比

选取终端碰撞角φfd分别为-40°，-60°，-80°，收敛时间tf=30 s，制导增益N=3，可调参数η=3。图7给出了不同期望碰撞角下的导弹运动轨迹、制导加速度、碰撞角误差和视线角变化曲线。

图7 不同期望碰撞角的仿真结果

由图7(a)和图7(c)～(d)可知，在所设计制导律的作用下，导弹实现了以期望收敛时间和终端碰撞角约束的攻击任务。由图7(b)可知，期望碰撞角的绝对值越大，导弹制导加速度变化越平缓。

碰撞角不同时的导弹能量消耗如表3所示。由表3可知，期望碰撞角的绝对值越大，导弹能量消耗越少。这是因为期望碰撞角的绝对值越大，其与比例导引所得的终端碰撞角之间的误差越小，能量消耗自然越少。

表3 碰撞角不同时的导弹能量消耗

4 结 论

针对具有收敛时间要求的碰撞角约束制导律设计问题，本文在PPN的基础上，结合任意时间收敛方法设计了ATC-IACG。在该制导律的导引下，导弹终端碰撞角可以在设定的时间内收敛到0，并通过多种场景的仿真验证了所提制导律的有效性。ATC-IACG形式简单、参数较少、灵活度高、物理意义明确，具有潜在的工程应用价值。另外，任意时间收敛方法还可以用于设计寻的制导律、飞行时间约束制导律或多弹协同制导律等，本文所提制导律也可以扩展至打击匀速或慢速移动目标。