Large positive magnetoresistance in photocarrier-doped potassium tantalites
2022-12-28RuiShuYang杨睿姝DingBangWang王定邦YangZhao赵阳ShuanHuWang王拴虎andKeXinJin金克新
Rui-Shu Yang(杨睿姝), Ding-Bang Wang(王定邦), Yang Zhao(赵阳), Shuan-Hu Wang(王拴虎), and Ke-Xin Jin(金克新)
Shaanxi Key Laboratory of Condensed Matter Structures and Properties and MOE Key Laboratory of Materials Physics and Chemistry under Extraordinary Conditions,School of Physical Science and Technology,Northwestern Polytechnical University,Xi’an 710072,China
Keywords: photocarriers,large positive magnetoresistance,extreme quantum limit
1. Introduction
The magnetoresistance(MR)effect has been extensively studied since its discovery in 1856. This effect can be used in sensors, memory devices, and the emergent physics of complex interactions. Many different MRs, such as ordinary MR,[1,2]anisotropic MR,[3,4]tunnel MR,[5]giant MR,[6]and colossal MR[7,8]have been investigated in magnetic and multilayer materials. Generally,the positive and conventional MR has a magnitude of only a few percent. It is even negligible in some nonmagnetic materials due to the curving of the carrier trajectory by the Lorentz force. Nevertheless, a large and linear MR effect breaks this familiar rule. It has been observed in several non-magnetic semiconductors,such as Si,[9]Bi,[10,11]PtBi2,[12]and graphene,[13]raising many lively discussions in the fields of condensed physics and functional materials. Moreover, the kind of MR in nonmagnetic materials can avoid Barkhausen noise in magnetic recording and sensor devices.
Complex oxides have extraordinary and multifunctional properties, including colossal MR in manganites, high-temperature superconductivity in cuprates, and multiferroics.[14–19]Among these materials, KTaO3(KTO)exhibits a cubic structure with a lattice constant of 0.3989 nm and a high dielectric constant(∼4500). These characteristics make it a promising material for the extreme quantum limit(EQL)under a high magnetic field and at low temperatures.[20]In particular, such a material could integrate its functions in the emerging electronics for all-oxide devices.[21,22]Due to ionic liquid gating or Ar+bombardment, the surface of KTO possesses a spectrum of emergent phenomena, such as electrostatic superconductivity,the topological Hall effect(THE),and de-Haas oscillation.[23–26]Recently,KTO has been used in the engineering design of two-dimensional electronic systems.Many heterointerfaces based on KTO have been studied, involving EuO/KTO,[27,28]LaTiO3/KTO,[29]LaVO3/KTO,[30]amorphous-LaAlO3/KTO,[31]and LaAlO3/KTO.[32,33]They show intriguing properties,such as two-dimensional superconductivity,high-mobility spin-polarized electron gas,the THE,and the anomalous Hall effect. However,the MR in these systems is usually small,with a value less than 10%.[34–37]And a reliable large MR effect in complex oxides has not been found so far.
In this work,we find,for the first time,a significant positive MR effect in KTO single crystals with photocarrier doping under high magnetic fields(about 12 T).Under 360 nm illumination with different light intensities at different temperatures,KTOs come into the EQL state, where the electrons are confined in the lowest Landau levels. In the temperature range of 2 K–50 K, KTOs exhibit metallic behavior and their Hall coefficient vanishes as the magnetic field increases.[38]
2. Experiment details
KTO(100)and(111)single crystals(3 mm×3 mm)with different thicknesses are commercially available. The electrical connections were realized at their surface using the ultrasonically wire-bonded aluminum wires. Both the resistivity and the Hall effect were measured with a van de Pauw geometry under 360 nm illumination with different light intensities.We used a physical property measurement system (CFMS-14T) that was equipped with an optical fiber. This apparatus is shown in the inset of Fig. 1(a). The bandgap (Eg) of KTO is 3.4 eV, and the wavelength of light is 360 nm (3.44 eV).Thus,the electrons can be promoted from the valence band to the conduction band under 360 nm light. Although the light illumination generates non-equilibrium carriers,a steady-state quasi-equilibrium can be achieved because the carrier lifetime is close to 0.15 ms.[39]This lifetime is much larger than thermalization. The holes are straightforward to trap, and thus the transport is dominated by electrons.[20,39,40]Furthermore,Hall measurements confirm that electrons mainly determine the conduction. More importantly, the interaction between light and matter depends on the optical properties of matter and the wavelength of light. The optical penetration depth is deduced from the absorption coefficient (α) of KTO, as shown in the supplementary material in Fig. S1(a), which is taken from Ref.[39],from which the depth profile of the electronic distribution can be estimated. From the absorption coefficient, we can obtain that the thickness of the conductive layer is larger than 1 mm atλ=360 nm. At this wavelength,the carrier density distribution, which is perpendicular to the surface of the samples, is uniform. Here, we define MR=[ρxx(H)−ρxx(H=0)]×100%/ρxx(H=0). The supplementary material in Fig.S1(b)shows the relationship between MR andHwhen the magnetic field is perpendicular and parallel to the current at 20 K, indicating that the samples exhibit isotropic properties. Considering the thickness of the conductive layer, the electric conduction of KTO under 360 nm light is quasi-three-dimensional. Additionally, LaAlO3/KTO heterointerfaces were prepared using pulsed laser deposition at 800◦C and 1×10−3Pa of O2with a KrF excimer laser(λ=248 nm)that operated at 1 Hz.
3. Results and discussion
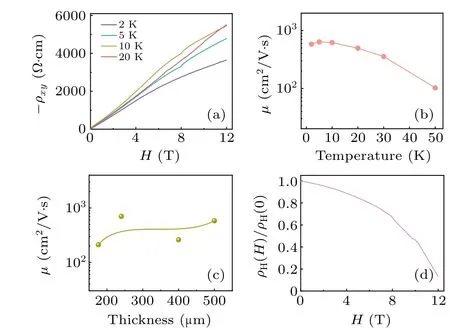
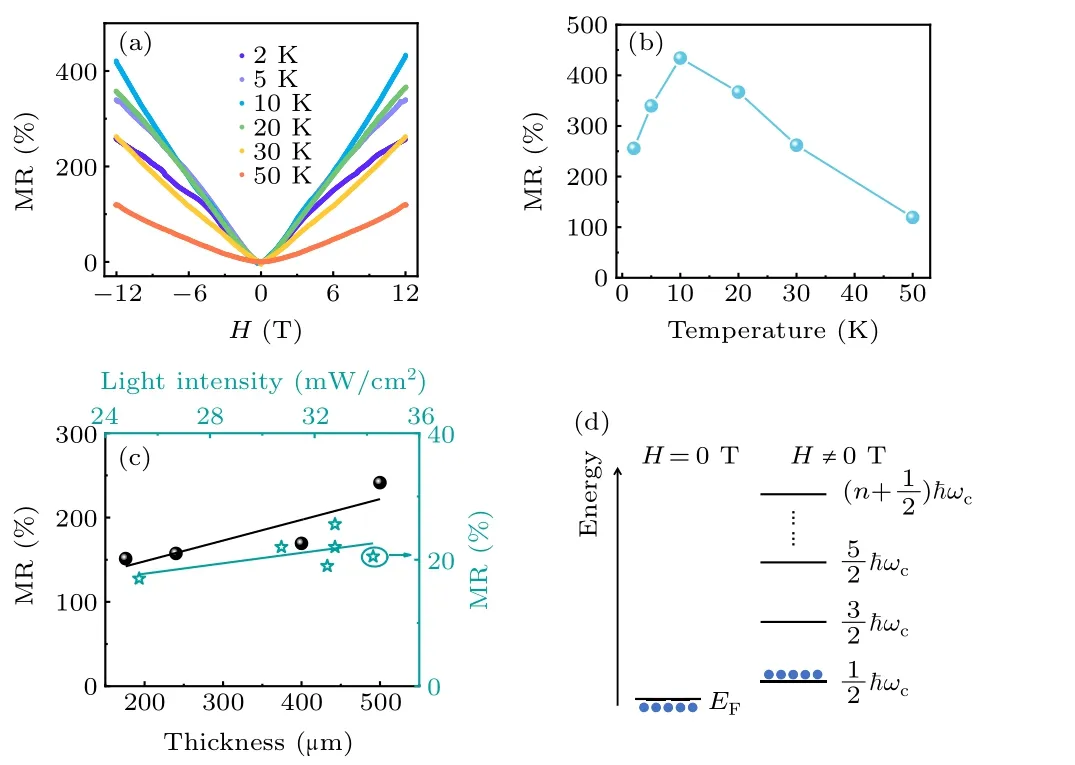
The temperature dependences of the electrical resistivity of KTO (100) and (111) are shown in Fig. 1(a). The inset shows a schematic diagram of the measured resistivity and Hall resistivity. We observe that the KTOs show metallic behavior at low temperatures. The temperature dependence of the electrical resistivity can typically be described by a power law,ρ=ρ0+ATn.[41]Whenn=2, the expected behavior is a Fermi liquid, while a ‘non-Fermi liquid’ is identified with 1 To analyze the electronic transport of KTO(100)by photo doping, we measure the Hall resistivity (ρxy) under the magnetic field (H). Figure 1(b) shows this behavior at different temperatures. Strikingly, theρxy–His nonlinear below 20 K. The carrier density (n) and mobility (µ) can be obtained from the Hall coefficient at a zero magnetic field. As shown in Fig. 1(c), the carrier density slightly decreases as the temperature decreases, while the mobility increases and reaches 1200 cm2/V·s at 2 K. More importantly, the KTOs still exhibit metallic behavior, even at very low electron densityn=1.4×1012cm−3.We also measured the carrier density and mobility of KTO single crystals with various light intensities at 2 K. Figure S2 demonstrates that the carrier density increases with the light intensity,which is consistent with previous research of STO single crystals.[42] Fig.1. (a)The temperature dependence of the resistivity of KTO(100)and(111) under illumination at λ =360 nm and 33 mW/cm2. The inset of (a)shows a sketch for the measurements of resistivity and Hall resistivity. (b)Hall resistivity(ρxy)of KTO(100)under the illumination as a function of the magnetic field at different temperatures. (c)Carrier density(n)and mobility(µ)of KTO(100)as a function of temperature. The Hall resistivity of KTO (111) as a function of the magnetic field in the temperature range of 2 K–20 K is shown in Fig. 2(a). The Hall resistivity (ρxy) favors a nonlinear dependence at low temperatures. The mobilities of KTO (111)as a function of thicknesses and temperatures are shown in Figs.2(b)and 2(c),respectively. The mobility is enhanced as the temperature decreases and the thicknesses increase. Generally, the nonlinear Hall effect has two origins: one is the abnormal Hall effect caused by magnetism, and the other is caused by the coexistence of two or more types of carriers.The abnormal Hall effect can be determined by the derivative relationship betweenρxyandHif the derivation curve has a peak near 0 T.[43]We exclude the abnormal Hall effect according to the curves of dρxy/dH(Fig.S3). To further investigate the nonlinear Hall effect,the two-channel conduction from the electronic bands is taken into account. It is found that the fitting result cannot explain the nonlinear Hall effect (Fig. S4 and Table S1). Thereby, the relationship between the magnetic field and the normalized Hall coefficient is analyzed, as shown in Fig.2(d). The normalized Hall coefficient decreases with the increasing magnetic field, which is consistent with reports by Kozukaet al.[38]The decreasing Hall coefficient is probably caused by the low level of scattering under a high magnetic field in the EQL. Fig. 2. (a) Hall resistivity (ρxy) of KTO (111) under the illumination as a function of the magnetic field in the temperature range of 2 K–20 K.(b)and(c)The mobility of KTO(111)as a function of temperatures and thicknesses at 0 T under the illumination with λ =360 nm and 33 mW/cm2,respectively.(d)The normalized Hall coefficient of KTO under illumination as a function of the magnetic field at 2 K. The requirements to realize the EQL state areωcτ>1 and ¯hωc>kBT,EF, whereωc=eH/m∗is the cyclotron frequency (eis the elementary charge,His the magnetic field,andm∗is the electron effective mass),τis the carrier relaxation time,kBTis the thermal energy, andEFis the Fermi energy. In this work, the dielectric constant (εr) of KTO is∼4500(2 K)[20]andm∗is 0.8m0.[20,40]Thus,the¯hωcof KTO is estimated about 2.78 meV,which is far larger thankBT(2 K)(0.18 meV). TheEFof KTO is about 5.4×10−4meV according to ¯h2k2F/2m∗. In addition, if we apply the Mott criterion to ¯hωc>kBT,EF, the EQL state can be realized by satisfying the following conditions:εr/mr>1.3×103,whereεr=ε/ε0(ε0is the vacuum permittivity)andmr=m∗/m0(m0is the bare electron mass). For the KTOs,the value ofωcτis∼1.44 at a high magnetic field because of the high mobility(>103cm2/V·s). Further,theεr/mris about 5.6×103,which is larger than 1.3×103. Therefore,KTO is likely to come into an EQL state. Electronic wave functions are highly localized and the small gyration radius of electrons in the perpendicular direction reduces the probability of scattering between electrons. Hence, the Hall coefficient decreases as the magnetic field increases. Figure 3(a) shows the relationship between the MR of KTO(100)and the magnetic field. The results for KTO(111)are shown in Fig. S5. The MR displays giant positive linear non-saturating features. As shown in Fig. 3(b), the MR increases nonlinearly when decreasing the temperature.The MR values with a thickness of 500µm under the magnetic field of 12 T are 256%,340%,433%,367%,263%,and 119%at 2 K,5 K, 10 K, 20 K, 30 K, and 50 K, respectively. These values are far greater than that of the ordinary MR effect. The reduction of MR below 10 K might be attributed to the localization of electrons due to the ferroelectric phase of KTO.[44]This phenomenon is consistent with the drop in carrier density. Furthermore,we measured the MR of KTOs with different thicknesses and light intensities at 2 K.Figure 3(c)shows that the MR of KTO (111) reaches∼200% (12 T) with different thicknesses and∼20%(2 T)at various light intensities(25 mW/cm2–35 mW/cm2). These values are far greater than those of oxide interfaces.[24,29] Fig.3. (a)MR of KTO(100)as a function of the magnetic field at different temperatures. (b) MR of as a function of temperatures with KTO (100) at 12 T.(c)The MR of KTO(111)dependence of different thicknesses(12 T)and light intensities(2 T)at 2 K;the solid lines are linear fitting curves. (d)A schematic diagram of the energy level under H =0 T and H /=0 T. All the electrons occupy only the lowest Landau level and other levels are empty when ¯hωc ≫EF. Early in 1959,Lifshits and Peschansky[45]proposed that the linear MR effect could be caused when the Larmor radius of electrons was smaller than their mean free path for a metal in a high magnetic field. Further, Abrikosov declared[46,47]that the system would reach the EQL state for a material with a smallm∗if the magnetic field was very high.This conjecture assumes that all of the electrons would occupy only the lowest Landau energy level in a gapless semiconductor with a linear energy spectrum. This will produce a linear MR with a magnetic field,ρxx∝H.Following this,various theories have been proposed to explain the positive MR in nonmagnetic materials by mechanisms,including electric field inhomogeneity,[48]density inhomogeneity,[49]density fluctuations,[50]and antiferromagnetic fluctuations.[51]In our work, although the carrier density is very low, the photocarrier-doped KTO favors metallics at low temperatures because a combination of a smallm∗and a large dielectric constant can push the insulator–metal transition boundary to low densities.[9]The electrons are distributed below the Fermi surface whenH=0 T, as shown in Fig. 3(d), andEFdecreases asHincreases. At such a low carrier density and high magnetic field, the Fermi energy ofEF= 5.4×10−4meV is very low. Thus, the lowest Landau energy, ¯hωc=2.78 meV, is far larger thanEF. At this time,the electrons occupy the lowest Landau level,and all the other levels are empty. As a result, KTO shows a quantum MR effect.[13,46,52]A non-saturating MR further verifies that the system of photocarrier-doped KTO comes into the EQL state. Another interpretation is the inhomogeneity in bulk or films,[48–51]which might arise from the carrier-density inhomogeneity,mainly caused by the light distribution from an uneven surface. To further analyze our experimental results,we measured the MR of STO single crystals and LaAlO3/KTO heterointerfaces under 360 nm light illumination. Figure S6 shows that single crystal STO and LAO/KTO exhibit no significant and linear MR under the same conditions. Although we cannot rule out the contribution of light inhomogeneity to the large linear MR, the experiment illustrates very interesting results for KTO under 360 nm irradiation, which further proves that KTO is a novel material with large positive MR based on complex materials. In summary,KTO single crystals exposed to 360 nm light show metallic behavior at low temperatures with very low carrier density and high mobility. We conclude that these photodoping KTOs reach the EQL state, which therefore provides a new oxide material with EQL. Importantly, we discover a significant positive MR effect and the decreasing of the Hall coefficient at low temperature and a high magnetic field. In particular,the MR value of KTO(100)reaches 433%at 10 K under 12 T. This is caused by all the electrons occupying the lowest Landau level in the EQL state. At the same time, we consider the contribution of light inhomogeneity to the large linear magnetoresistance. This work paves a way to the understanding of the fundamental physics of the interaction between light and complex materials. Acknowledgments Project supported by the National Natural Science Foundation of China(Grant No.51572222),Key Research Project of the Natural Science Foundation of Shaanxi Province,China(Grant Nos. 2021JZ-08 and 2020JM-088), the Natural Science Basic Research Plan in Shaanxi Province of China(Grant No. 2021JM-041), and the Fundamental Research Funds for the Central Universities (Grant Nos. 3102017OQD074 and 310201911cx044).
4. Conclusion
杂志排行
Chinese Physics B的其它文章
- Fault-tolerant finite-time dynamical consensus of double-integrator multi-agent systems with partial agents subject to synchronous self-sensing function failure
- Nano Ag-enhanced photoelectric conversion efficiency in all-inorganic,hole-transporting-layer-free CsPbIBr2 perovskite solar cells
- Low-voltage soft robots based on carbon nanotube/polymer electrothermal composites
- Parkinsonian oscillations and their suppression by closed-loop deep brain stimulation based on fuzzy concept
- Temperature dependence of spin pumping in YIG/NiO(x)/W multilayer
- Interface effect on superlattice quality and optical properties of InAs/GaSb type-II superlattices grown by molecular beam epitaxy
