Tunable terahertz acoustic-phonon emission from monolayer molybdenum disulfide
2022-12-28ChengXiangZhao赵承祥MiaoMiaoZheng郑苗苗YuanQie郄媛andFangWeiHan韩方微
Cheng-Xiang Zhao(赵承祥) Miao-Miao Zheng(郑苗苗) Yuan Qie(郄媛) and Fang-Wei Han(韩方微)
1College of Physics and Information Engineering,Shanxi Normal University,Taiyuan 030031,China
2School of Medical Information Engineering,Jining Medical University,Jining 272067,China
Keywords: acoustic-phonon emission,terahertz,monolayer molybdenum disulfdie
1. Introduction
High-frequency acoustic-phonons have a wide range of applications. For example,they can be used to study the optical,acoustic and topological properties of some materials[1,2]and detect the interface of different materials,[3]the thickness of layers,[4]the band gap and the sound velocity of test samples.[5,6]They can also be used for ultra-fast switching.[7]Hence, to realize these applications, it is significant to find high-frequency acoustic-phonon sources.
Significant efforts have been made to develop highfrequency acoustic-phonon source devices. Sound amplification by stimulated emission of radiation based on the semiconductor superlattices[8–10]and thin-film material[11]has been suggested as the means to obtain high-frequency acousticphonons. It has also been proposed that the acoustic-phonons excited by electrons–phonons interaction in solids can be generated and amplified.From the standpoint of condensed matter physics,acoustic-phonon emission or absorption occurs in the process of acoustic-phonons interacting with electrons. The electrons transition from one state to another as they interact with phonons. Net acoustic-phonon emission can be obtained if the electron velocity exceeds the acoustic-phonon velocity, which is known as the Cerenkov acoustic-phonon emission. A variety of works have indicated that terahertz(THz) acoustic-phonons can be obtained via Cerenkov emission from, for example, GaAs,[12]three-dimensional Dirac system,[13]graphene,[14]quantum wire (well),[15,16]and heterojunction structure.[17]In addition to the above materials,it is still significant to find outstanding materials that can generate high-frequency acoustic-phonons.
Monolayer molybdenum disulfide (ML-MoS2),[18]as a two-dimensional material with a direct band gap,high carrier mobility and high switching ratio,has been considered to have promising applications in field effect transistors. Note that the acoustic-phonon velocity[19]in ML-MoS2is higher than that in conventional semiconductors such as GaAs,[12]and is lower than that in graphene.[20]This suggests that the frequencies of acoustic-phonons generated by ML-MoS2are between the frequencies of those generated from GaAs and graphene because the acoustic-phonon frequencyωqis related to phonon velocityvasωq=v|q|,whereqis the wave vector of phonon in material.Moreover,the acoustic properties of ML-MoS2have not yet been explored completely for the time being. Therefore,it is necessary to study the acoustic-phonon emission from MLMoS2to check whether it can be used as a high-frequency acoustic-phonon source.
In this work, we presented a theoretical study of the acoustic-phonon emission from drifting electrons in MLMoS2driven by a direct-current electric field by applying the Boltzmann equation (BE) method. We studied the distribution of acoustic-phonon emission intensity along with phonon frequency and phonon emission angle in different driving electric fields and electron densities. We found that the Cerenkov emission of THz acoustic-phonon can be observed when the electron velocity exceeds the phonon velocity in ML-MoS2under a very weak electric field. The acoustic-phonon emission spectrums in different electric fields and electron densities were obtained and the physical mechanisms of acousticphonon emission were analyzed from the perspective of condensed matter physics. We compared the acoustic-phonon emission from ML-MoS2with those from graphene and GaAs.The results suggested that the acoustic-phonon emission from ML-MoS2can make up for those from graphene and GaAs.Furthermore,ML-MoS2can be used in tunable hypersonic devices such as terahertz phonon sources.
2. Theoretical considerations and methods
Here, we consider a gate-controlled ML-MoS2system as shown in Fig. 1(a).[21]The conducting carriers in MLMoS2are electrons in the presence of a positive gate voltage and the electron density in ML-MoS2can be tuned by the applied gated voltageVg. A driving direct-current electric fieldFx=VSD/L, whereLis the length from source to drain electrodes,is applied and taken along thex-direction of the ML-MoS2sheet by applying source to drain electric voltageVSD. According to the view of condensed matter physics,acoustic-phonon emission or absorption occurs in the process of phonon interacting with electrons, whilst the electron will transition from one state|k〉to another state|k′〉as shown in the Schematic diagram Fig. 1(b). In this work, we consider that electrons interact with acoustic-phonons via unscreened deformation potential coupling and the electrons transition within the conduction band because the valence band is completely occupied. The semi-classical BE is taken as the governing transport equation to study the acoustic-phonon emission from drifting electrons in ML-MoS2driven by the electric field. The BE in non-degenerate statistics takes the form
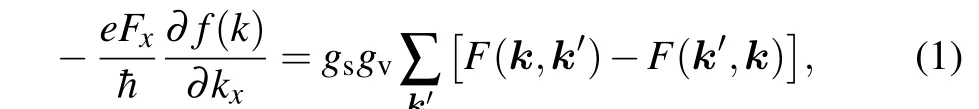
whereeis the charge of an electron. ¯h=h/(2π) withhbeing the Planck constant.gs=2 andgv=2 account, respectively, for spin and valley degeneracy.F(k,k′)=f(k)[1−f(k′)]W(k,k′) withf(k)=[e(¯h2|k|2/(2m∗)−µ)/kBTe+1]−1being the momentum-distribution function of the electrons in the state|k〉with momentumk=(kx,ky). Because the electrons are accelerated or even heated when subjected to a driving electric field, so the original equilibrium distribution of electrons is not maintained. The original equilibrium momentumdistribution function for electrons can be described approximately by the following drifted energy distribution functionf(k)≈f[E(k∗)],wherek∗=(kx −kv,ky)withkv=m∗vx/¯hbeing the momentum drifted by electron velocityvx, andE(k)= ¯h2|k|2/(2m∗)is the energy of an electron in the conduction band, withm∗=0.48mebeing the effective mass of an electron in the conduction band for ML-MoS2,[19]andmeis the mass of an electron. Considering that the electrons are heated and the temperature isTe, we takeµas the chemical potential of this electron system and determineµby the condition of electrons number conservation.[22]The intra band transition rate for electron interaction with acoustic-phonon can be obtained from the Fermi’s golden rule as

where + and−correspond to the absorption and emission of acoustic-phonon, respectively. ¯hωq=vs|q| is the energy of the acoustic-phonon withs=l(t)representing longitudinal(transverse) acoustic-phonon andqbeing the wave vector of acoustic-phonon. The square of the matrix element for electron interaction with acoustic-phonon is[19]

whereρ= 3.1×10−7g/cm−2is the mass density of MLMoS2,Ξt=1.6 eV andΞl=2.8 eV are the deformation potential constants for the transverse acoustic(TA)and longitudinal acoustic(LA)phonon,respectively.vt=4.2×105cm/s andvl=6.7×105cm/s are the TA and LA phonon velocity,respectively.[19]
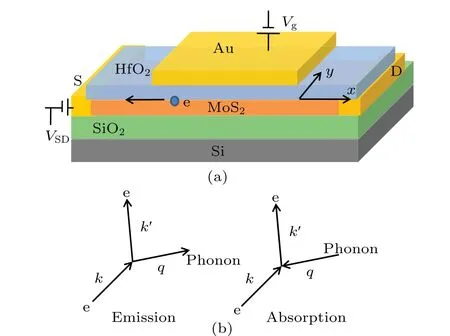
Fig.1. (a)Theoretical model considered in this work. ML-MoS2 covered with HfO2 is placed on SiO2/Si substrate. HfO2 is introduced between ML-MoS2 and the Au electrode to serve as the top gate dielectric layer. S and D are the source and drain electrodes. Electron(e)moves in plane of ML-MoS2 when source to drain electric voltage VSD is applied to ML-MoS2. (b) Schematic diagram of phonon emission and absorption.

whereP(ωq,θ)=P+(ωq,θ)−P−(ωq,θ) is the distribution function of net acoustic-phonon emission intensity, which is the difference between acoustic-phonon emission and acoustic-phonon absorption, andθis the acoustic-phonon emission angle(i.e.,the angle betweenqand thex-axis). Furthermore,

3. Results and discussion
The drift velocityvxand temperatureTeof electrons can be obtained by solving the energy and momentum balance equation self-consistently.[22]However, it is arduous to do such work. In this work, we takevxandTeas input parameters. The two parameters are obtained from Refs.[23,24],in which the heating effect of the electrons in ML-MoS2by the driving electric field is considered. These theoretical results are in consistent with the experimental results.[21]As shown in Fig. 2, owing to the hot carrier effect when electrons respond nonlinearly to the electric field,Tevaries withvxand the electric fieldFx.[24]Their temperature will be higher than the lattice temperature under high electric fields. The electron velocityvxtends to be saturated under high electric fields due to the electron–optical phonon scattering. More importantly,we noticed that the drift velocityvxof electrons in ML-MoS2can exceed the acoustic phonon velocityvsunder very weak electric fields (0.2 kV/cm for LA phonon and 0.12 kV/cm for TA phonon) for which the electrons are even in the linear response region. This suggests that the Cerenkov acousticphonon emission from ML-MoS2can be easily observed under a low electric field.
Figure 3(a)shows the spectrum of acoustic-phonon emission. Two peaks of the LA and TA phonon emission can be observed. The LA and TA phonon emissions are distributed in the THz region. However, compared with the TA phonon emission,the LA phonon emission is distributed in the higherfrequency region and the LA phonon emission intensity is higher than the TA phonon emission. This is because the LA phonon velocity is higher than the TA phonon velocity. Moreover, the deformation potential constants for the LA and TA phonons in ML-MoS2areΞl=2.8 eV andΞt=1.6 eV,[19]and the square of the matrix element for electron interaction with acoustic-phonon is proportional to the square of deformation potential constant as shown by Eq. (3). This induces that the LA phonon emission intensity is quite different from the TA.We note that the peaks of the spectrums of LA phonon emission from graphene[14]and GaAS[12]are,respectively,located at∼1.0 THz and∼15.0 THz. The frequenciesωqof acoustic-phonons generated by ML-MoS2are between the frequencies of those generate by graphene and GaAs. Because the acoustic-phonon velocityvsin ML-MoS2is between those in graphene and GaAs,and the acoustic phonon frequencyωqis related to phonon velocityvsasωq=vs|q|. Furthermore,the acoustic-phonon emission is angle-dependent because the drift velocity of the electron along the opposite direction of the driving electric field leads to the breakdown of the system symmetry.This angle-dependent is determined by the momentum and energy conservation during the interaction between electron and phonon. Figures 3(b)–3(d)show the angular and frequency distributions of acoustic-phonon emission for different electric fields. Notice the following: (1) The strongest acoustic-phonon emission can be observed atθ=0◦(i.e.,the direction in which the electrons are moving). This implies that in ML-MoS2, the generated acoustic-phonons propagate mainly in the direction in which the electrons move. (2) The intensity of acoustic-phonon emission reduces by decreasing emission angle and enhances with increasing electric field for all emission angles. These results in Fig. 3 indicate that the THz acoustic-phonon emission from ML-MoS2can be realized and tuned by applying a driving electric field.

Fig. 2. Drift velocity vx and temperature Te of electrons for different electric fields Fx at lattice temperature T =50 K.The data are obtained from Refs.[23,24]. vl and vt are, respectively, the LA and TA phonon velocity. The drift velocity vx of electrons in ML-MoS2 can exceed the LA phonon velocity vl and TA phonon velocity vt when the applied electric fields are about 0.2 kV/cm and 0.12 kV/cm.
Figure 4 shows the frequency distributions of the LA and TA phonon emission intensity. Note that the electron velocity can exceed the velocity of LA and TA phonon in ML-MoS2by applying a very weak electric fieldFx ∼0.2 kV/cm and∼0.12 kV/cm, as shown in Fig. 3. Therefore, the Cerenkov emission of acoustic-phonons can be generated from MLMoS2with a very weak electric field and the emission intensity is significantly enhanced with the increase of electric field as indicated in Fig.4. This result suggests that the interaction between electrons and acoustic-phonons enhanced with the increase of the electric field. According to the condensed matter physics, the generation of the Cerenkov acoustic-phonon emission means a net energy transfer from electron to phonon during the interaction between electron and phonon. Both the electron velocity and electron temperature increase with increasing the electric filed as shown in Fig.2. This causes the interaction between electrons and phonons and the emission intensity to increase as the electric field increases. In addition,both the LA and TA phonon emission exhibit a blue shift with the increase of the electric field,which indicates that the drifting electron tends to interact with higher-frequency acousticphonon with increasing electric field. These results in Figs.3 and 4 indicate that ML-MoS2exhibits special acoustic phonon properties compared with other materials such as graphene and GaAs. Therefore, the acoustic-phonon emission from MLMoS2can make up for those from these materials and MLMoS2can be used in tunable hypersonic devices such as THz acoustic phonon sources.
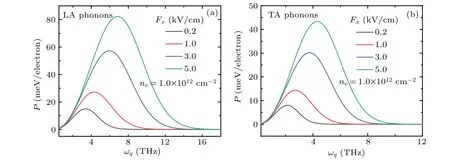
Fig.4. Frequency distribution of(a)LA and(b)TA phonon emission for different electric fields Fx under a fixed electron density ne and a fixed emission angle θ=0◦.The corresponding electron velocities are 0.724×106 cm/s,2.621×106 cm/s,4.653×106 cm/s,and 5.507×106 cm/s.Temperatures are 53.22 K,65.13 K,90.39 K,and 111.95 K.[23,24]
Figure 5 shows that both the LA and TA phonon emission intensities increase with increasing electron densityneas a result of the enhancement of the interaction between electron and phonon. However,as shown by the blue and red curves in Fig.5,the emission intensity changes little in the low electron densities. Moreover,the electron transition,from one state to another within conduction band by electron–phonon interaction,occurs mainly around the Fermi energy. The increase of electron density leads to the increase of the Fermi energy and the energy of electrons that interaction with phonons. This results in the enhancement of the electron–phonon interaction and the blue shift of both the LA and TA phonon emission intensity. The results in Fig.5 suggest that the acoustic-phonon emission from ML-MoS2can be tuned not only by the driving electric field, but also by the electron density that controlled by the applied gate voltage.

Fig. 5. Frequency distribution of (a) LA and (b) TA phonon emission for different electron densities under a fixed electric field and a fixed emission angle θ =0◦.
It should be noted that the data in Fig.2 are obtained from Refs. [23,24] in which the electron–acoustic phonon scattering, electron–optical phonon scattering and electron-electron screening have been taken into account in calculating the relationship among electron velocity, temperature and electric field. We applied the obtained electron velocity and temperature to calculate the acoustic phonon emission during the interaction between electron and acoustic phonon. Consequently,the calculation of acoustic phonon emission in our work is carried out considering the electron–optical phonon scattering. In fact,there may be other scattering mechanisms for an electron system. For example, the electron–charged impurity scattering can effect the mobility of electron especially at low temperatures,[21,25–27]slow down the electrons and decrease the temperature of the electrons. This weakens the electron–phonon interaction and leads to the reduction of phonon emission intensity.
4. Conclusions
In this work,we have presented a theoretical study of the acoustic-phonon emission from ML-MoS2driven by a directcurrent electric field and applied the BE method. The major conclusions of this study are as follows: (i)The Cerenkov emission of THz acoustic-phonons can be generated from MLMoS2under the action of a relatively weak electric field. (ii)The strongest acoustic-phonon emission can be observed in the direction in which the electrons move. (iii) The intensity of the Cerenkov acoustic-phonon emission is significantly enhanced with increasing electric field for all emission angles.(iv)The spectrum of THz acoustic-phonon emission from MLMoS2can be controlled by the electric field or the electron density tuned by the applied gate voltage. (v) The frequency of generated acoustic-phonon from ML-MoS2is higher than that from GaAs and lower than that from graphene. The results suggest that in respect of acoustic-phonon emission,MLMoS2can make up for graphene and GaAs and be used in tunable hypersonic devices such as terahertz phonons sources.We hope our theoretical work can be verified by experiments.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant No. 11604192), the Fundamental Research Program of Shanxi Province, China (Grant No.202103021224250),the Science and Technology Innovation Project of Colleges and Universities of Shanxi Province of China(Grant No.2020L0242),and the Start-up funding from Shanxi Normal University(Grant No.0505/02070351).
杂志排行
Chinese Physics B的其它文章
- Fault-tolerant finite-time dynamical consensus of double-integrator multi-agent systems with partial agents subject to synchronous self-sensing function failure
- Nano Ag-enhanced photoelectric conversion efficiency in all-inorganic,hole-transporting-layer-free CsPbIBr2 perovskite solar cells
- Low-voltage soft robots based on carbon nanotube/polymer electrothermal composites
- Parkinsonian oscillations and their suppression by closed-loop deep brain stimulation based on fuzzy concept
- Temperature dependence of spin pumping in YIG/NiO(x)/W multilayer
- Interface effect on superlattice quality and optical properties of InAs/GaSb type-II superlattices grown by molecular beam epitaxy
