数据挖掘技术在初中物理成绩评定中的应用

马小花，霍 杰

宁夏大学物理与电子电气工程学院，银川 750021

初中生自控力差、叛逆性较强、学习状态不稳定，因此，分析学生教育数据，预测学生的学习状况，及时提醒异常学生非常有必要。中学班级规模基本在五十到六十人之间，师生比例较低，教师不易了解学生的学习近况。而考试可以监测和促进学生的学习，但需要对学生的考试成绩进行客观评定和合理预测。文章利用N评价和马尔可夫链方法对学生考试数据进行分析和预测，并通过具体的案例分析成绩数据，实时地把分析结果反馈给教师，来评估中学生对知识的掌握能力和应用水平。

1 采用N评价方法评定学生个体学习效度

1.1 成绩测量分析

2 采用马尔可夫链模型评价学生学习效度的理论基础

2.1 马尔可夫链的建模思想

马尔可夫链评估法：某一事件在时刻t0所处的状态为已知条件，过程在时刻t>t0所处状态的条件分布与过程在时刻t0之前的状态无关[4]。它是一种以概率论和随机过程理论为基础，运用随机数学模型来分析现实活动发展变化过程中的数量关系的一种统计方法。

选取初二学生为研究对象，之前其他学科的成绩与当前学习物理课程的状态无关，即某中学初二第一学期学生物理考试成绩具有马尔可夫性或无后效性，可利用齐次马尔可夫链进行预测。马尔可夫链方法进行计算的一个必要过程是转移概率，它是指一个马尔可夫链在同一时间内不能有两个以上的状态。但是，它可以从一个状态转移到另一个状态，称为从Sn状态到Sn+1状态的转移，即马尔可夫链表示从时间n到时间n+1可以转移到不同状态或保持相同状态[4]。

2.2 马尔可夫链的建模步骤

首先，统计两个班级在等级 A、B、C、D、E 中的人数。其次，将两次考试成绩中不同等级的相互间变化量值进行整合。之后，可以明确得出由i到j等级的转移概率

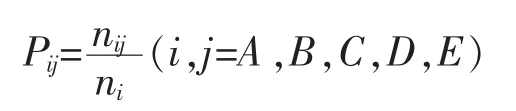
其中，ni是相应等级的人数，nij表示由i到j等级变化的学生人数。在计算转移概率的矩阵时，需要统计出每次考试成绩分布的状态向量。最后，排除不稳定性因子，给出两次成绩转移频数[5]。

在学生考试成绩中，要去除两次测量结果中存在的不稳定性因子。例如，甲同学第一次考试成绩为30分，第二次成绩为90分以上，两次成绩相差较大，存在各方面不确定性因素。但是，马尔可夫链模型要求的数据必须是平稳发展的。因此，在数据初步筛选过程中要注重数据的可靠性分析[5]。

3 以某中学初二年级1、2班物理课程成绩分析研究

3.1 数据介绍

研究对象为初二年级1班和2班两个班级，两个班均有53名学生，所收集的4次物理成绩皆为单元测试成绩。4次物理单元测试卷的具体考核内容如表1所示，表2为试卷题型及题目设置数量概况表。

表1 单元测试卷考核内容表

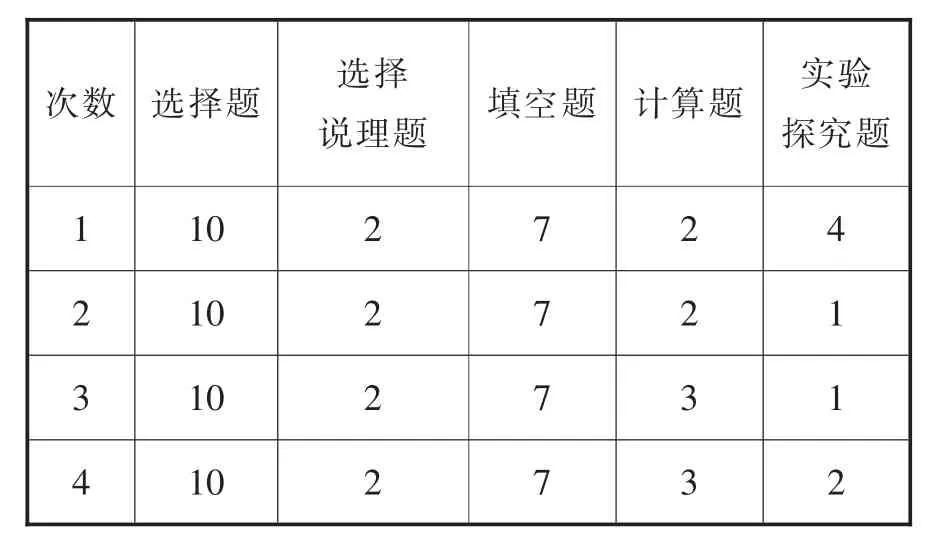
表2 试卷题型及题目数量表

选用可靠性统计克隆巴赫Alpha系数来检验测试卷的内部一致性，即项目同质性。表3为两个班级试卷的信度，从成绩数据中得到4套试卷的内部一致性系数（克隆巴赫Alpha系数）。两个班的一致性系数达到0.938以上，良好的信度水平说明4套试卷内容设置具有一致性。

表3 可靠性统计

3.2 测量学生个体动态物理成绩的案例研究

从1班随机挑选5个学生，统计其4次考试的原始分数，进行4×5阶矩阵计算

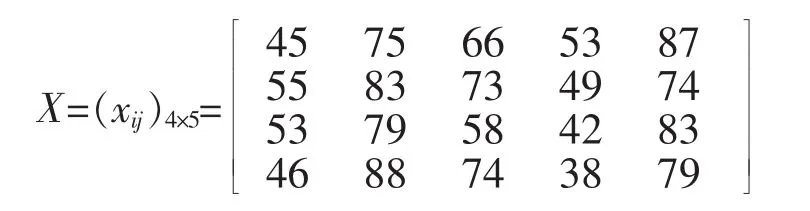
基于初二（1）班物理学科考试数据，可得出5个学生在4次考试中的平均分=（65.2 66.8 63.0 65.0）， 标准差 σj=（15.025 12.718 15.633 19.473）。 进而根据得出标准成绩，如表4所示。

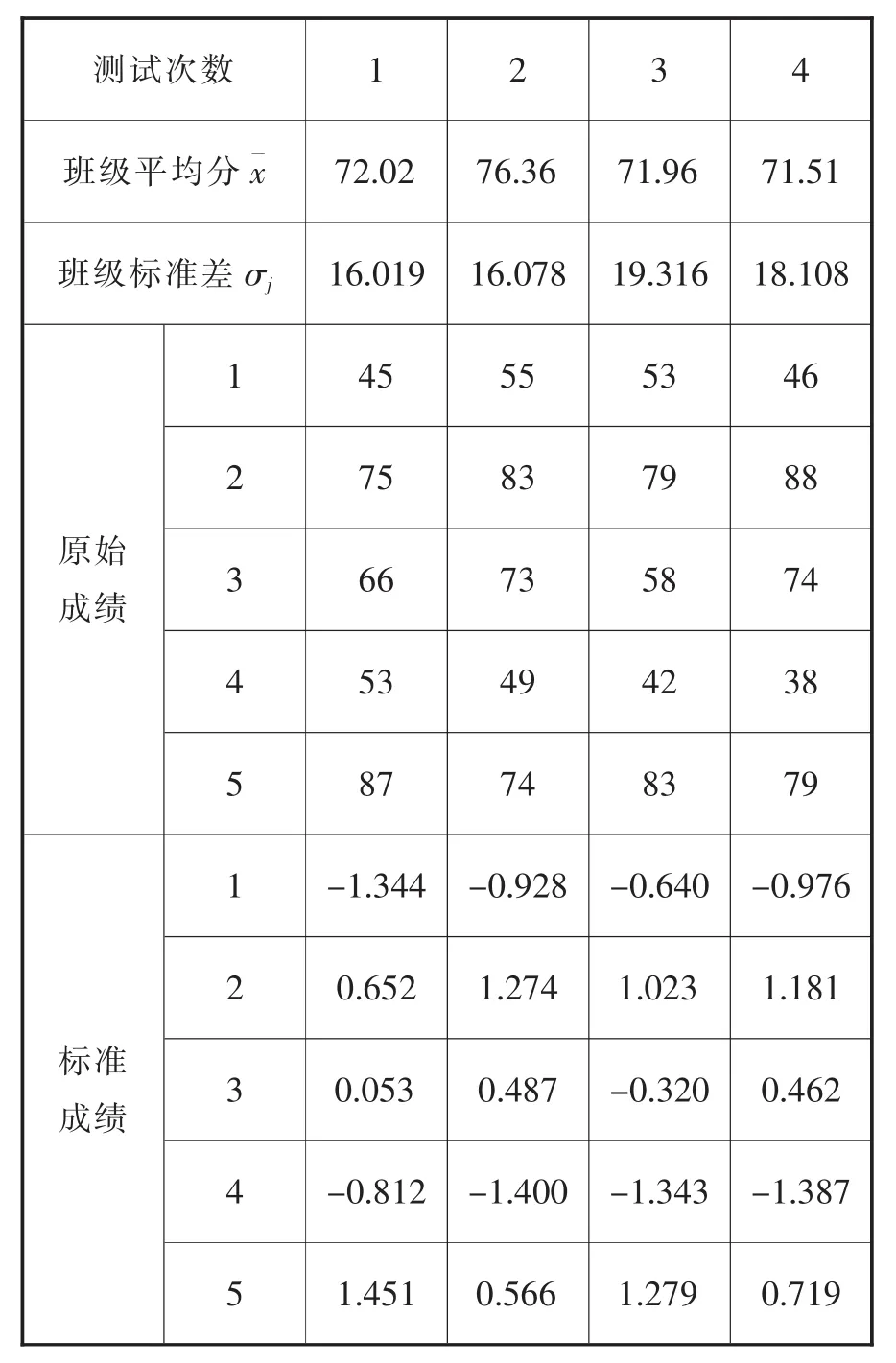
表4 5个学生初二第一学期4次物理测验情况

首先，通过计算得出5个学生进步程度的估计值分别为：0.139，0.134，0.042，-0.167，-0.148。然后，根据公式计算出5个学生进步程度的具体分数。结合实际测试成绩，部分学生在考试中的进步程度不同。通常取β=2，去掉估计值中的负值，使分析数据更加精准。

上述进步程度估计值中 max（bi）=0.139，可以得出5个学生的进步分数分别为

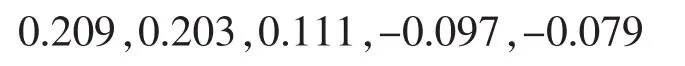
表明5个学生在初二（1）班第一学期物理期末总评中，第一个学生成绩进步最大，第四个学生成绩退步最大。进步分数b*i分别为

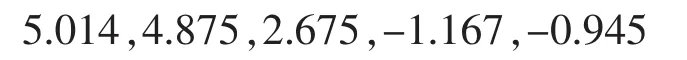
利用N评价模型计算进步分数b*i的基础上，结合班级平均成绩的排名情况和每次测验的进步值对班级排名进行综合测量[3]。设每次测验的权重系数fi为25%，则有

可得

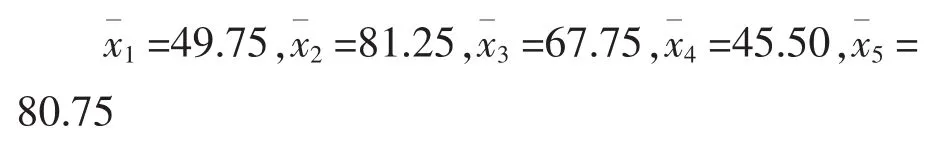
则5个学生的N分数为

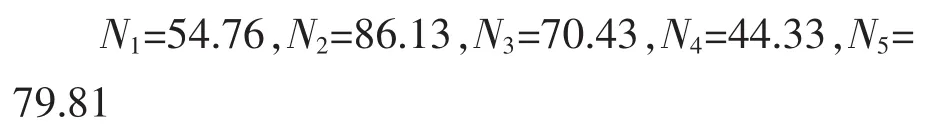
3.3 采用马尔可夫链方法评价两个班级学生的学习效果

首先将成绩划分为5级，分别如下所示：A级（90-100 分）、B 级（80-89 分）、C 级（70-79 分）、D 级（60-69分）、E 级（0-59分），并分别显示对应等级学生的比例，如图1所示。图中频数表示每次考试中不同成绩等级中的学生数量。

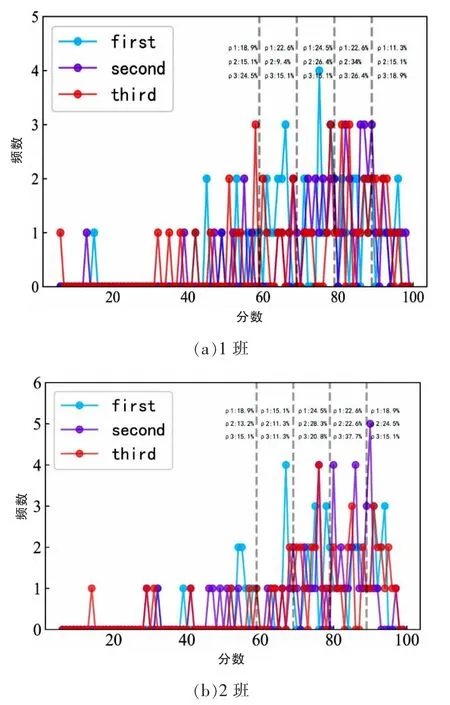
图1 两个班三次成绩的概率密度分布

表5和表6是1班和2班3次物理考试成绩及状态转移表，可求出前三次考试成绩中1、2两班的状态向量。

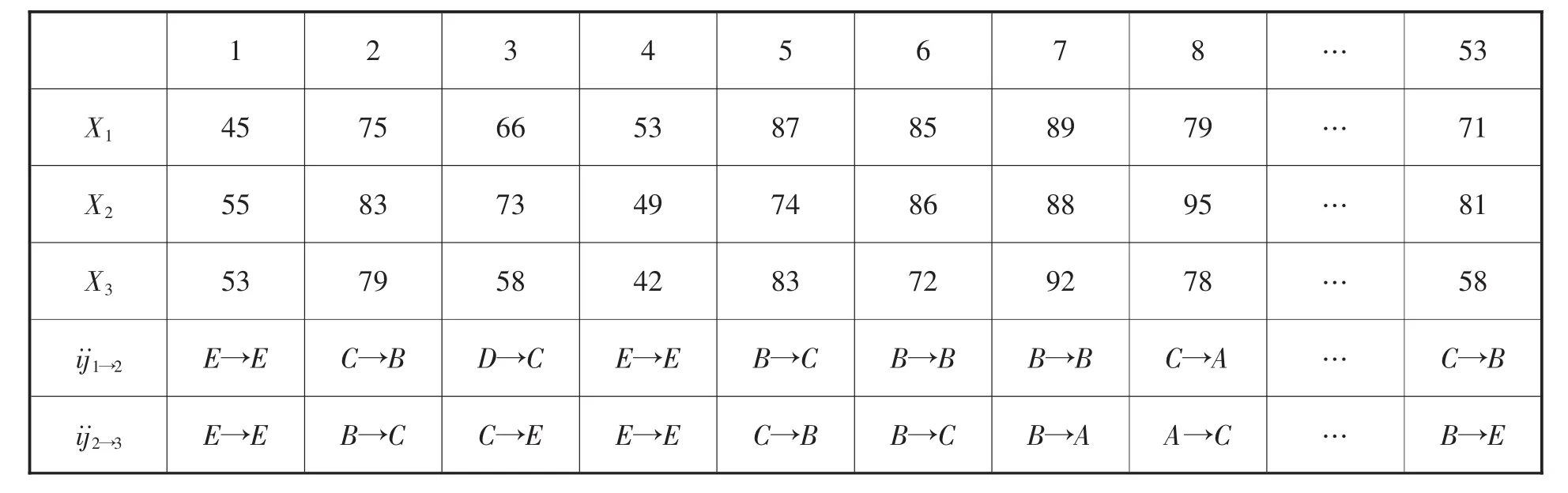
表5 1班物理考试成绩及状态转移表

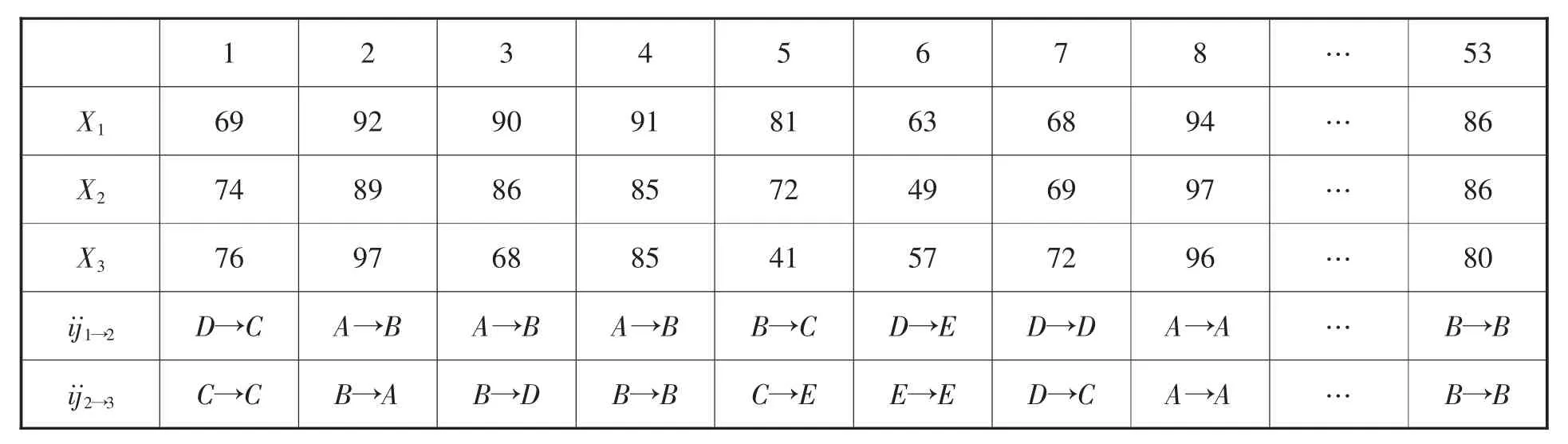
表6 2班物理考试成绩及状态转移表

P2→3代入得

为了进一步评估教学效果，进行指标的量化。

对每个等级确定分值，如90分记为“优”，80分记为“良”，70 分记为“中”，60 分记为“及格”，50分以下记为“不及格”。

初始各分数段内的平均成绩乘以相应的权重向量，可以预测出1、2班第四次的物理综合成绩

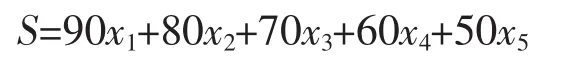
结果为

4 结果分析与启示

上述分析结果如图2所示，五个学生在传统考试评定成绩下，成绩分别为

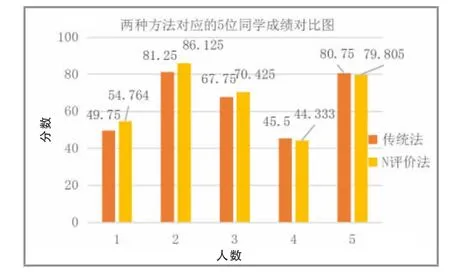
图2 两种方法对应的5个学生成绩对比图

利用N评价方法得出五个学生考试成绩分别为

通过该方法可以全面、客观地评定学生一学期期间的学习效果，从而针对性地补短板、强弱项，提升学生学习物理的积极性。还可以帮助学生明确在此阶段的学习状态，并为他们合理规划下一阶段的学习目标及努力方向。

经计算，1班和2班的第四次平均成绩分别为71.51分和71.91分。马尔可夫链方法预测1班的第四次平均分为67.747，误差为5.26%；预测2班的第四次平均分为73.993，误差为2.9%。这表明，马尔可夫链方法可以较为准确地预测成绩走势。

以上两种方法作为评定学生个体和教师教学质量的分析方法，利用学生个体一学期学习成绩来反馈学生对于知识点的内化程度，从而判断教师实施的教学模式和教学策略是否有效，使得教师能够对教学信息有定量的认识。