基于强化学习的非正交多址接入和移动边缘计算联合系统信息年龄更新

李保罡 石 泰* 陈 静 李诗璐 王 宇 张天魁

①(华北电力大学 保定 071003)

②(国网河南省电力公司许昌供电公司 许昌 461000)

③(北京邮电大学 北京 100876)

1 引言

随着车载网络、虚拟现实等实时应用的发展，信息年龄(Age of Information, AoI)成为衡量信息新鲜度的一个重要标准。它被定义为目的端接收的最新更新信息自产生后所经过的时间[1]。由于在智能工厂、智慧型监控等创新应用中，终端设备不再是简单的数据收集，而是经过数据处理才能显现出所需的状态信息，因此，在AoI中引入计算受到了人们的广泛关注[2]。考虑到终端设备有限的电池容量和计算资源，移动边缘计算(Mobile Edge Computing, MEC)被认为是一种处理终端设备计算问题的有效解决方法[3]。在当前物联网的场景中，例如无人驾驶、超清视频和增强现实等，MEC可以满足这些任务的高计算要求，而非正交多址(Non-Orthogonal Multiple Access, NOMA)技术的应用能够更进一步减少多任务卸载延迟的问题。对于MEC与AoI的结合方面，部分学者已经做了少量研究。为了实时捕获新鲜的状态信息，Li等人[4]利用无界约束马尔可夫方法解决状态采样和卸载处理的问题。Liu等人[5]提出了一个基于状态更新的Q学习算法可以有效地解决如何获取状态更新的情况。Song等人[6]设计了一个包含单个MEC服务器和单个移动设备的系统，并提出一种轻权重任务调度和计算卸载算法以解决年龄最小化的问题。然而，上述文献只考虑到任务调度和计算资源分配对AoI的影响，没有涉及如何使用有限的频谱资源进一步减少AoI的情况。

非正交多址接入被认为是一种有效提高频谱利用率的方法，随着研究的深入，NOMA与AoI的结合逐渐引起了广泛的关注[7]。NOMA的思想是在同一频谱资源中多个用户可以同时被服务。在不需要更多无线资源的情况下，NOMA传输能够使多个用户的AoI下降[8]。文献[9]对NOMA和传统正交多址接入(Orthogonal Multiple Access, OMA)环境下的平均AoI做了比较，这是NOMA应用于AoI的第1次尝试。文献[10,11]研究了AoI在NOMA和OMA网络中的性能表现，根据AoI的定义，数据的生成和传输的调度都起着很关键的作用。NOMA被认为是处理大规模物联网部署的一种很有前途的技术[12,13]。NOMA的思想是利用功率域，使多个用户在同一时间或者频带内得到服务，与OMA相比，NOMA可以通过提高频谱利用率来降低AoI[14]。Pan等人[15]研究了基于NOMA的状态更新系统，经过分析发现，在高信噪比和中信噪比的情况下，NOMA能够实现更新鲜的信息更新。Gómez等人[16]设计了一个在源节点和目的节点之间的队列传输模型。在传输过程中，为了降低总体的AoI，NOMA被用来进行节点间的功率分配。将NOMA引入到AoI中，虽然考虑了频谱资源的限制，但是却忽视了边缘计算在降低AoI方面的作用。

目前，已经有越来越多的文献在不同的场景下最小化AoI，然而很少有文献在NOMA-MEC联合系统中研究AoI问题。因此，本文综合考虑计算资源和频谱资源对AoI的作用，在此基础上，引入干扰的问题，通过设计一种联合优化卸载因子和卸载功率的策略，让所有设备的平均更新代价最小。考虑到环境动态变化这种更现实的场景，采用多代理深度确定性策略梯度(Multi-Agent Deep Deterministic Policy Gradient, MADDPG)算法用于分配卸载任务量和卸载功率。最后给出性能仿真结果与分析。

2 系统模型

2.1 网络模型

如图1所示，在这个系统中考虑一个多设备的MEC系统，它由移动设备的集合N、1个装配有MEC服务器的接入点(Access Point, AP)和1个干扰者J组成。其中，N=|N|是移动设备的数量。移动设备D可以监测物理过程的当前状态(例如利用摄像机记录十字路口的交通情况)，在这个过程中需要进行数据处理。假设这个系统可以分成多个时隙，t ∈T={0,1,...,T −1}，每个时隙的长度为τ。在每个时隙开始时，设备可以从环境中采集当前的数据。移动设备可以选择处理原始数据按照本地计算或者卸载给边缘服务器计算的方式进行处理。αi(t)∈[0,1]表 示设备i的卸载因子，当αi(t)=0时，表示数据在设备i处完全进行本地计算；αi(t)=1，表示数据完全卸载给AP进行计算。所有设备的卸载决策可以表示为α(t)=[α1(t),α2(t),...,αN(t)]。在卸载过程中，所有设备的卸载功率分配决策为P(t)=[p1(t),p2(t),...,pN(t)] ,其 中pi(t)∈[0,Pmax]表示设备i的卸载功率，Pmax是最大卸载功率。在每个时隙，设备使用计数器记录获得的信息年龄[10]。

图1 在多个设备中数据的安全传输

在卸载过程中，设备将受到干扰者的攻击。干扰者通过发射干扰信号阻碍设备与AP之间的通信，延长设备的卸载时间，从而使任务不能在一个时隙内完成，最终导致在一个时隙内状态更新失败。对于每个卸载设备，干扰者平均分配干扰功率。也就是说，当αi(t)̸=0时，即部分数据或者全部数据通过卸载给AP进行处理时，在时隙t，干扰设备i的干扰功率为

其中，PJ表示干扰者的总干扰功率， n表示选择卸载计算的设备数量。当αi(t)=0 时 ，pij(t)=0。即数据完全本地计算时，干扰者不发送干扰功率。

2.2 计算模型

在计算模型中，设备可以通过本地计算或者卸载计算来处理原始数据。

2.2.1 本地计算

最后，经过边缘服务器处理后，可以得到计算结果。由于计算结果的数据量很小，传输速度较快，因此，传输时延可以忽略不计。

因此，设备i处理任务的时延可以表示为

2.3 状态更新模型

在每个时隙t，设备通过处理计算任务来获得状态更新。如果计算任务能在这个时隙内完成，则状态信息被更新；否则，设备没有状态更新。在这部分，利用信息年龄来测量状态更新的新鲜度。在这个多设备MEC系统中，AoI反映在设备处生成最新被执行的任务，到被处理，最终在设备处获得计算结果所经过的时间。采用Ai(t)=t −θi(t)表示设备i的信息年龄。其中θi(t)是指设备i产生最新任务的时间戳。信息年龄的演变展示在图2中。

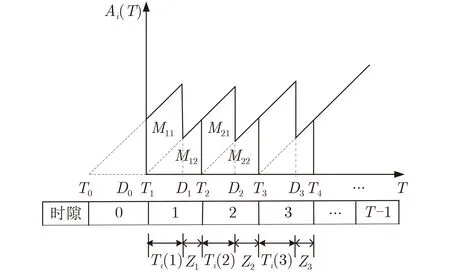
图2 信息年龄的演变

3 优化问题

在本部分，优化的目标是在计算资源、处理时延和用户能耗的约束下最小化平均更新代价，即

由式(11)和式(14)可知，平均更新代价与处理时延有关，而处理时延受到卸载任务量和卸载功率的影响。因此，在多设备的MEC系统中，需要通过优化卸载决策和卸载功率来最小化平均更新代价。在上面的公式中，C1和C2分别表示卸载决策和卸载功率的取值范围。C3和C4分别表示利用卸载计算或者本地计算处理的任务需要在一个时隙内完成。C5表示通过优化变量来抵抗干扰攻击，降低传输时间，使卸载时间不超过一个时隙，确保在一个时隙内完成状态更新。C6保证所有设备的总能耗不超过设置的最大能耗。而C7保证分配给卸载设备的计算资源总和不超过MEC服务器的计算容量。由于在不同的时隙下，信道条件等变量是随着时间动态变化的，传统的优化方法难以解决动态变化的场景。而强化学习能有效地解决这一问题。因此，采用强化学习算法来优化卸载决策和卸载功率，从而使目标函数最小。

4 MADDPG算法

强化学习是单个代理与未知环境相互交互，使长期奖励最大化的一种有效方法。通过不断地尝试，它可以让单个代理学习到最优的行为。强化学习由3个必要的变量组成：状态，动作，奖励。在每次迭代过程中，代理将从环境中选择当前的状态信息，将它作为输入值，然后选择一个动作，环境会根据选择的动作值反馈给代理一个奖励，用来评价当前动作的好坏。通过反复的试错，代理会倾向选择使长期奖励增加的动作[17]。

在多设备的MEC系统中，本文将每个设备视为一个代理，设备之外的一切被视为环境。考虑到卸载速率、设备的总能耗和MEC服务器计算容量的影响，其他设备的决策会对当前代理产生影响。由此可以看出，欲最小化平均更新代价，需要多个代理的相互协作才能实现。然而，在多代理的环境中，传统的强化学习是不适用的。这是因为在传统强化学习中，每个代理只考虑最大化自身的奖励，没有考虑其他代理的影响。针对这一问题，多代理强化学习可以提供一个有效的解决方法。多代理强化学习允许多个代理通过相互协作来实现它们的目标。结合当前场景，状态、动作和奖励对应如下：

状态：在时隙t，代理i观察网络的情况，并且选择下面的参数构成网络的状态。

在本文中，由于动作的取值是连续的，需要采用基于策略的算法进行求解。考虑到有大量的设备需要处理自身的计算任务，因此，代理的数量是非常大的。基于策略的演员-评论家算法(Actor-Critic,AC)在单代理的环境中表现良好，但是随着代理数量的增加，方差也会变大，所以不适用于多代理的环境。而多代理深度确定性策略梯度算法是AC算法的一种变体，通过让智能体之间集中训练以及分布运行，它可以处理动态环境中环境与代理相互交互的问题，在代理i做决策时，会考虑其他代理的影响。通过多个代理间协作，共同最大化奖励值。针对上述优势，采用MADDPG算法来寻找最优的动作值，从而达到最小化目标函数的目的。

在MADDPG算法中，利用经验回放机制降低样本之间的相关性。通过代理与环境的交互，可以获得经验序列(st,at,rt,st+1)， 其中st,at,rt分别对应状态、动作和奖励。st+1表示下一个状态。所有代理的经验被存储在经验回放内存D中。在训练过程中，从D中随机抽取小批经验序列进行学习。MADDPG算法主要是由AC的框架组成。在演员A中，它主要由在线策略网络和目标策略网络组成。确定性策略µ直接从每步的动作中获得。在评论家C中，它也主要由两个网络组成：在线Q网络和目标Q网络。对于演员框架，在线策略网络的更新主要由策略梯度来完成，策略梯度的表达式为

在评论家框架中，在线Q网络的参数由损失函数进行更新，损失函数的表达式为

5 仿真结果分析

在该部分，本文考虑不同工作模式、卸载功率和不同算法对平均更新代价的影响。在这个场景中，设定设备被随机地分布在200 × 200 m2的区域内，与服务器相连的AP位于该区域的中心，干扰者在AP的附近。输入任务的大小Di(kbit)服从(100,500)之间的均匀分布，处理1 bit数据所需的CPU周期数为2 ×103cycle/bit。信道带宽为2 MHz，相应的噪声功率σ2= 3×10−13。另外，可利用的MEC服务器的计算容量F(t)设置为10 GHz/s。在本地计算阶段，每个设备的CPU频率为0.2 GHz/s。在传输过程中，单位干扰功率的代价w为0.1，总干扰功率PJ设置为20 W。仿真参数如表1所示。

表1 仿真参数设置

图3展示了在设备数量设置为10，3种卸载因子的作用下，不同MEC计算容量对平均更新代价的影响。这3种卸载因子分别表示本地计算(α= 0)，部分卸载(α= 0.5 )和完全卸载(α= 1)。由图3可以看出，随着MEC服务器计算容量的增加，部分卸载和完全卸载的长期平均代价都逐渐减小，而本地计算的长期平均代价保持不变。这是因为当MEC服务器的计算容量增加时，更多的设备可以通过将计算任务卸载给MEC服务器处理来获得状态更新。并且，对于仅本地计算来说，每个设备的状态更新不受MEC服务器计算容量的影响。因此，通过部分卸载的方式和适当地增加MEC服务器的计算容量，可以有效地降低平均更新代价。

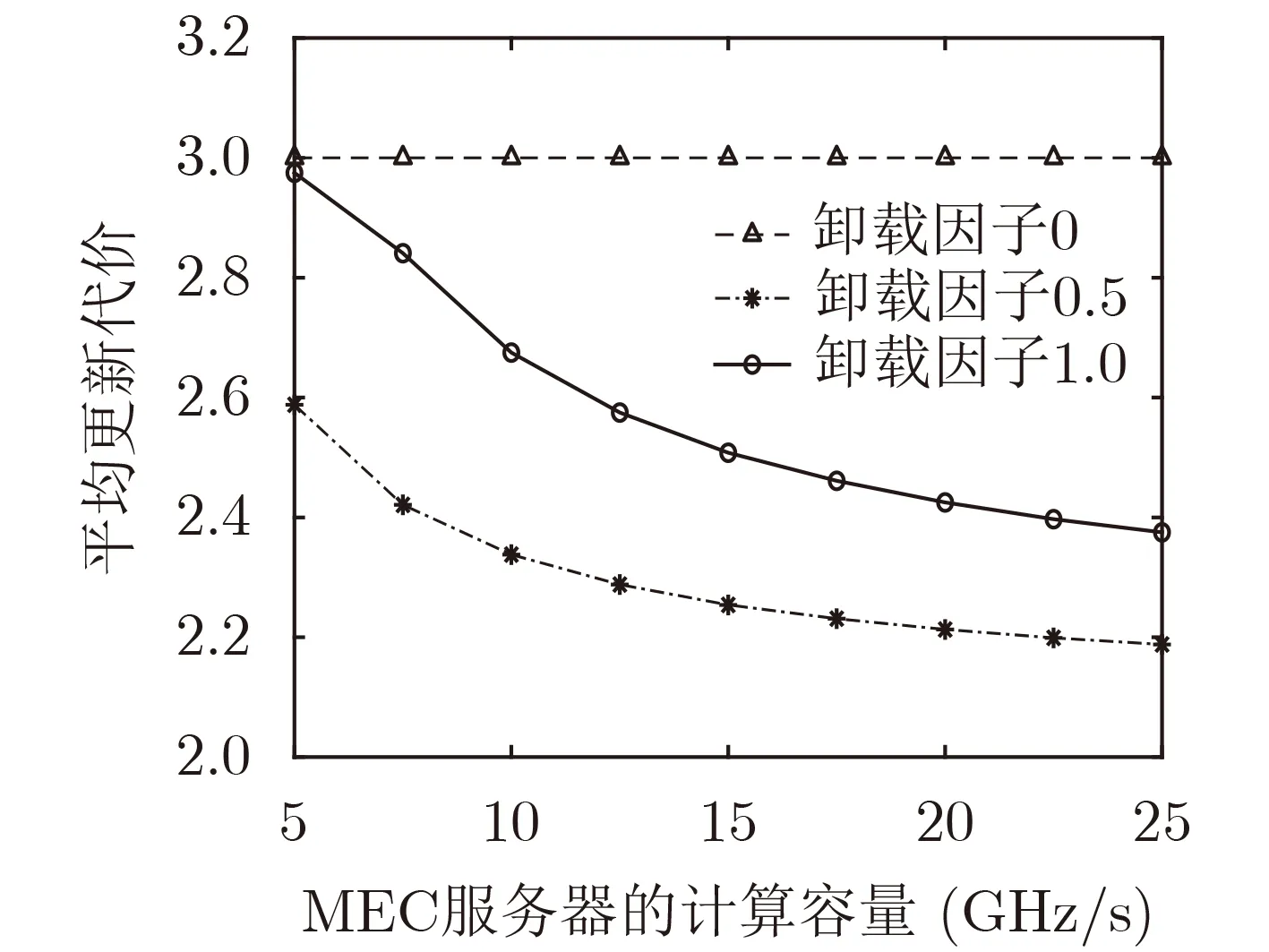
图3 计算容量对平均更新代价的影响

然后，考虑在部分卸载(卸载因子为0.5)的情况下，利用3种不同的方案去优化卸载功率从而使平均更新代价最小。这3种方案表示如下：

(1) MADDPG算法，即主要应用的优化方案。

(2) 演员-评论家算法(AC算法)：每个设备不知道其他设备的信息，在训练过程中，只知道自身的本地信息。

(3) Q学习算法：每个设备不知道其他设备的信息，适用于小规模离散动作空间的优化。

图4展示了在固定用户数量下，迭代次数和平均更新代价的关系。从图4可以看出，随着迭代次数的增加，平均更新代价逐渐减小。除此之外，MADDPG算法在降低平均更新代价方面优于其他两种方案。这是因为MADDPG算法考虑到多个代理之间的相互协作，通过代理间的共同作用，最大化奖励值。而AC算法和Q学习算法没有考虑到设备间的相互影响，只考虑自身的状态信息。从图4还可以看出，MADDPG算法的平均更新代价分别比AC算法和Q学习算法降低了37.5%和53.1%。

图4 迭代次数和平均更新代价的关系

图5表示不同设备数量对平均更新代价的影响。当设备数量在10～100逐渐增加时，3种算法的平均更新代价也是逐渐增加的。这是因为MEC服务器计算容量有限，随着设备数量的增加，每个设备获得的计算资源减少，因此导致处理时间增加，进而使平均更新代价增大。通过对图中数据分析可以发现，适当地减少用户数量，有利于降低平均更新代价。

图5 不同设备数量对平均更新代价的影响

6 结束语

本文基于NOMA-MEC联合系统，考虑到信息新鲜度的影响，对多设备单边缘计算服务器场景进行了研究。基于MADDPG算法，建立了最小化平均信息年龄的优化问题，提出一种寻优的卸载因子和卸载功率策略。仿真结果表明，利用部分卸载的方式，在降低平均更新代价方面效果最好。同时，与其他方案相比，采用MADDPG算法和降低设备数量均可有效地降低平均更新代价。提出的寻优的卸载因子和卸载功率策略可以很好地降低设备的信息更新代价，大大提高了设备的更新效率。