一种基于旋转不变子空间算法的非模糊参数配对方法

揭允康 叶晓东 王 昊 李 莉 陶诗飞

(南京理工大学电子工程与光电技术学院 南京 210094)

1 引言

2维频率估计和波达方向估计(Direction Of Arrival, DOA)在雷达、通信、电子对抗、生物医学等领域有着广泛的应用。在现有的2维估计方法中，基于子空间的估计算法具有优良的分辨性能，因此得到了广大学者的关注。如2维多重信号分类算法 (2-Dimensional MUltiple SIgnal Classification algorithm, 2D-MUSIC)[1–3]基于谱峰搜索，具有很高的分辨力和估计精度，然而在信号源维数增加时运算量也急剧增加；2维旋转不变子空间方法(2-Dimensional Estimating Signal Parameter via Rotational Invariance Techniques, 2D-ESPRIT)[4–8]、2维矩阵束方法 (2-Dimensional Matrix Pencil, 2DMP)[9,10]和2维传播算子方法 (2-Dimensional Propagator Method, 2D-PM)[11,12]等利用阵元结构实现了2维参数的分维处理，通过特征分解分别得到两组包含待估计参数信息的特征值。相比于MUSIC算法，基于特征值分维的ESPRIT类算法不需要进行谱峰搜索，在一定程度上降低了参数估计的复杂度，并且具有较高的分辨力。

但ESPRIT类算法的多维特征分解是互相独立的，直接得到的估计结果并不会一一对应，因此需要额外的步骤对估计结果进行配对。Rouquette等人[4]首先对2维参数的旋转因子矩阵进行线性组合，再利用特征矩阵的相关特性进行排序，然而配对过程中存在模糊参数，若参数取值不当就无法得到正确的配对结果； Hua[9]和王秀等人[10]利用噪声子空间与导向矢量的正交性实现2维参数配对，但是重复特征值会导致结果失配；Chen等人[13]通过构造分块矩阵将重复特征值与单特征值区分开来，然而同样存在判断特征值相等的模糊门限，文献[14]对其进行了详细的精度分析；Zoltowski等人[15]提出了一种基于酉ESPRIT算法的2维估计免配对算法，但并不适用于带有衰减因子的信号模型，且存在阵列中心对称的局限性；杨力强等人[16]提出了一种L型阵列下基于ESPRIT算法的2维参数配对方法，将矩阵以相同的特征矩阵同时对角化，通过对角线上元素的幅角进行排序来确定2维参数的配对顺序，然而在部分情况下仍然存在失配的问题。

近年来许多研究都利用文献[4,13,16]的方法进行多维参数配对[17–19]，然而上述方法仍然存在模糊参数，重复特征值导致失配等问题，因此本文提出了一种基于文献[4]配对算法的修正算法。本文算法将特征值线性组合后生成一个判断矩阵，根据矩阵不同维的对应关系，按信号信噪比高低进行搜索配对，因此具有较好的抗噪特性，在有多对重复特征值的情况下也能准确配对。本文算法结构简单，计算复杂度低，相比于文献[4,13]，没有模糊参数，相比于文献[16]，在存在多对重复特征值情况下也具备准确的配对能力，具有较高的实用性。

2 2维ESPRIT算法估计信号频率

本节先回顾2维频率估计问题和文献[4]的2维ESPRIT算法。假设待估计的2维复值正弦信号模型为

3 2维参数配对

4 仿真验证

仿真 1 设置信号个数K=3，频率分别为f1=[0.24, 0.24, 0.26], f2=[0.24, 0.26, 0.24],α1=[–0.03, –0.03, –0.06], α2=[–0.03, –0.06, –0.03],SNR=25 dB；采样参数M=N=20；矩阵参数P=Q=8。在每个条件下进行I=200次独立实验。为了比较不同算法的配对性能，将配对结果用2维散点图表示。以频率估计为例，如果配对结果集中在(0.24, 0.24), (0.24, 0.26), (0.26, 0.24)3个区域附近，说明配对结果正确。并且配对结果偏离3个点的距离也反映了估计结果的精度。

本文算法的配对结果由图1所示，图1(a)和图1(b)分别是衰减因子和频率的配对结果。由图1(a)可知，本文算法适用于带有衰减因子的信号模型，并且因为衰减因子与频率的配对结果一致。为了更加简便地比较算法配对性能，本文仅对频率配对结果进行分析。由图1(b)可以看到，200次独立实验中都没有出现(0.26, 0.26)配对错误的情况，验证了本文算法配对的准确性。本文算法配对过程中没有模糊参数，因此也验证了本文算法的非模糊性。

图1 本文算法的配对结果

为了说明模糊参数对估计结果的影响，对文献[4,13]算法原理进行分析，其配对结果分别如图2、图3所示。

文献[4]利用参数β将F1和线性组合以避免出现重复特征值，其中β的取值范围为(0, 1)，但是具体的数值并不能确定。若β取值不当，线性组合后的矩阵仍然存在重复特征值，导致配对错误或精度下降。为了直观比较不同β取值的配对性能，将算法估计精度用均方根误差(Root Mean Squared Error, RMSE)表示

由图2(a)可知文献[4]中β取值与均方根误差的关系，当β=0.35时，均方根误差最低；当β=0.50时，均方根误差最高。配对结果分别如图2(b)、图2(c)所示。可以看到图2(b)配对准确，估计精度较高，而图2(c)表明β参数取值不当会影响估计结果，导致算法估计精度降低。

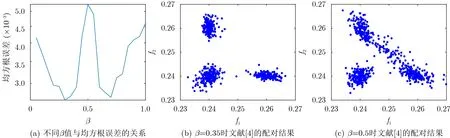
图2 文献[4]中不同β取值的配对结果

文献[13]首先需要根据特征值之间的欧氏距离判断是否存在重复的特征值，然而文中并没有给出判断门限ε的取值。当ε选取过大时，会将相近特征值看作相等特征值，导致虚警；当ε选取过小时，无法发现重复特征值，导致漏警。并且判断门限ε的最佳取值也会随着来波信噪比的变化而并不一致。在本算例中，对ε随机取3个数值来验证ε的取值对配对结果的影响。由图3可以看到，图3(b)中ε=0.05时配对结果较接近理想结果，图3(a)中ε=0.10时，存在(0.26, 0.26)配对错误的情况，图3(c)中ε=0.01时，算法估计精度较低。

图3 文献[13]中不同ε取值的配对结果

文献[16]提出了两种没有模糊参数的配对算法，并且相比已有的配对算法其准确率有明显改善[16]，图4是两种算法的配对结果。算法1对F1和F2′以相同的特征矩阵同时进行对角化，在低快拍时估计精度较低。算法2利用算法1估计结果的对角矩阵幅角顺序进行排序，具有较高的估计精度。由图4可以看到，算法1估计结果精度较低，算法2在本算例中能取得较好的估计结果。

图4 文献[16]算法配对结果

为了直观比较新算法的估计精度，本文算法，文献[4,13,16]配对算法的均方根误差随SNR的变化曲线如图5所示。由图5可以看到，除了文献[16]的算法1外，其余算法的最佳性能都近似相等，此时这些方法都能准确配对。但由前文分析可知，若文献[4,13]算法的参数选择不当，会导致估计结果失配或精度降低，相比之下本文算法的配对过程中并没有模糊参数，具有更高的实用性。

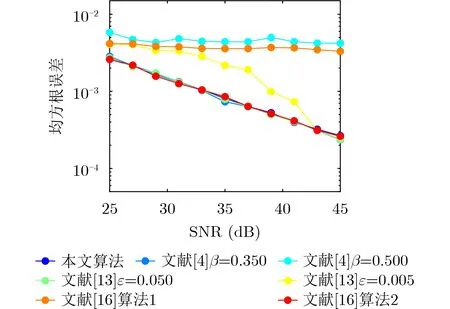
图5 不同算法均方根误差随SNR的变化

仿真 2 为了进一步比较本文算法和文献[16]算法2的配对性能，考虑存在多对重复特征值的情况：设置信号个数K=4；其频率分别为f1=[0.24,0.24, 0.26, 0.26], f2=[0.24, 0.32,0 .28, 0.32]；衰减因子α1=[–0.03, –0.03, –0.06, –0.06], α2=[–0.03,–0.09, –0.07, –0.09], SNR=25 dB；采样参数M=N=20；矩阵参数P=Q=8。每种方法进行I=200次独立实验。

本文算法，文献[16]算法2的配对结果如图6所示。文献[16]算法2利用了矩阵同时对角化的原理，然而如果F1存在重复特征值，其对角化的特征矩阵不是对角矩阵而是分块对角矩阵，在待估计参数相近的情况下，对角线上元素幅角的排序并不是正确的配对顺序。由图6(b)可以看到，文献[16]算法2出现(0.24, 0.28)，(0.26, 0.24)配对错误的情况。相比之下，本文的配对算法在有多对重复特征值时仍然具有准确的配对能力。

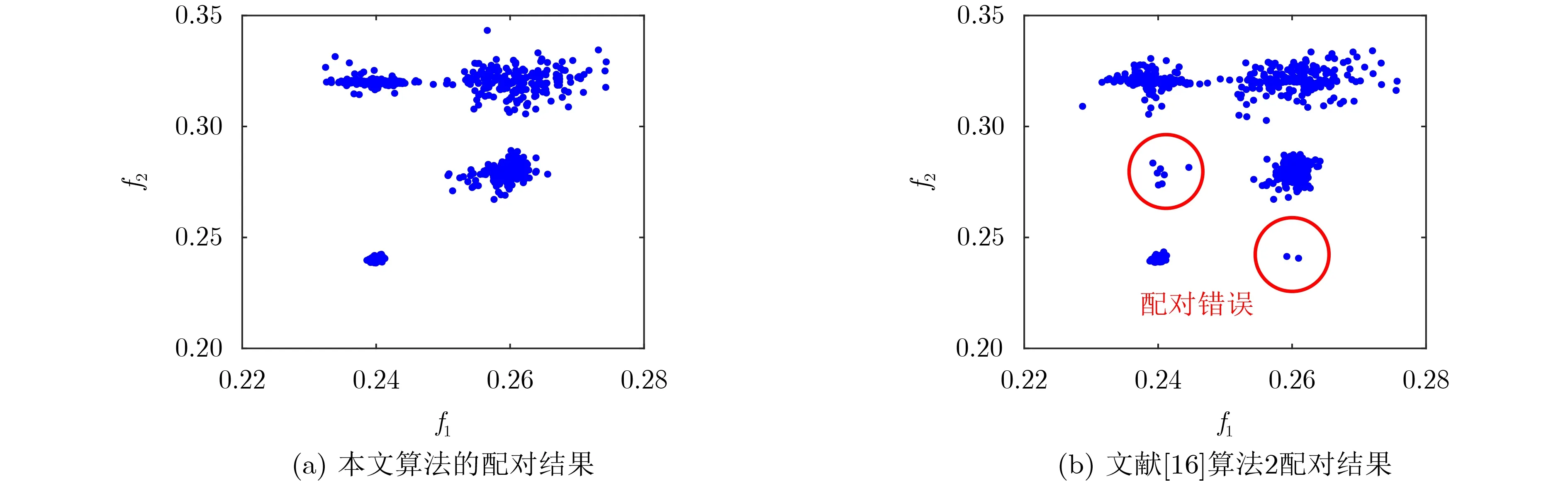
图6 不同算法配对结果

5 结论

本文提出一种基于ESPRTI类算法特征值分维的多维参数配对方法，有效解决了配对过程中存在模糊参数，以及特定情况下参数失配的问题。本文算法首先对包含参数信息的特征值进行线性组合，构造一个判断矩阵，再根据矩阵不同维对应关系实现多维参数的自动配对，具有较高的估计精度。仿真结果表明，相比已有的配对算法，本文算法在配对过程中没有模糊参数，在存在多对重复特征值时也能准确配对，具有更高的实用性。