高超声速滑翔飞行器机动状态识别方法研究

张君彪 熊家军 兰旭辉 陈 新 李 凡

①(空军预警学院预警情报系 武汉 430019)

②(95980部队 襄阳 441000)

1 引言

高超声速滑翔飞行器(Hypersonic Glide Vehicle, HGV)是指速度在6000 km/h以上，飞行空域在20～100 km的武器，以其高机动、大航程的特点打破了传统攻防平衡的态势，对现有防空防御体系造成了颠覆性影响，开拓了军事斗争的新领域和新形式[1]。世界各军事大国围绕HGV的研发正在展开激烈的军备竞赛。2021年5月，据美国“Breaking defense”上的文章，美陆军的“远程高超声速武器”导弹射程远超2775 km。此前，俄罗斯卫星通讯社报道，俄罗斯现已装备了“先锋”和“匕首”两种高超声速武器，分别采用陆基和空基进行发射。HGV的不断发展给各国空天安全造成了严重威胁，对HGV的跟踪、预测和防御成为研究热点[2]。对HGV机动状态识别进行研究是防御过程中非常重要的一个环节，可以为HGV的威胁估计、轨迹预测和防御决策提供有力支撑。

HGV机动状态识别实质上是一种分类问题[3]。现有关于空中目标机动状态识别的研究主要集中在常规飞行器，而对HGV机动状态识别进行研究的公开文献还非常少。HGV相对常规飞行器来说，速度更快，机动状态转换所需的空间范围更广，特征提取也相对更加困难。目前机动状态识别的方法主要有贝叶斯网络[4,5]、支持向量机[6,7]、随机森林[8]和深度学习模型[9,10]等。文献[5]对战机的机动特征进行了分析，建立了基于动态贝叶斯网络的机动动作识别模型，具有较好的实时性和准确性；文献[7]将直升机飞行状态分为10类，采用支持向量机对飞行状态进行识别，通过实飞数据对算法进行验证，算法的正确率较高；文献[8]对高超声速再入滑翔飞行器的运动特性进行研究，将目标运动状态分为6类，采用随机森林的方法对目标状态进行识别，得到了较高准确率；文献[11]将敌机机动动作进行分解，提出了一种基于随机森林和支持向量机的两级识别方法，分别对机动动作和战术动作进行识别，具有较好的识别效果。

上述方法在一定程度上为目标机动状态识别提供了解决方案，但它们在处理多维度、大数据量的输入数据时性能会明显下降。近年来，深度学习在特征提取、模式识别领域具有良好表现，尤其在处理多维、大批量数据和抗噪性上展现了独特优势[12,13]。文献[9]通过分析空中目标的机动特征和作战意图之间的对应关系，建立了深度神经网络的识别模型，对空中目标的机动特征进行识别进而得到作战意图，获得了较高的识别率；文献[10]设计了一种长短时记忆网络对车辆驾驶意图进行识别并对车辆轨迹进行预测，取得了较好的效果；文献[12]提出了一种运动行为识别网络的航迹估计算法，通过循环神经网络对飞行器运动行为进行识别，并根据识别结果选择相应的模型进行滤波，获得估计的航迹。

由于HGV机动状态识别的数据输入是一个多维的、大批量的时间序列数据，且通过雷达跟踪获取的数据含有一定噪声，因此本文提出了一种基于注意力卷积长短时记忆网络(ATtention Convolution Long-Short Term Memory network, AT-ConvLSTM)的HGV机动状态识别方法。首先，通过分析HGV机动特性，划定机动状态类别，生成轨迹库，并构造了包含高度、高度变化率、速度倾角、速度方位角、速度方位角变化率的特征参数集。然后，对雷达跟踪的HGV飞行数据进行特征提取和转换，进而得到5维的特征识别参数序列数据。最后，设计了一种基于AT-ConvLSTM的HGV机动状态识别模型，并在雷达跟踪数据集中进行测试，验证所提模型在机动状态识别中的有效性。

2 HGV机动建模

2.1 HGV滑翔段运动方程

假设大地模型为均匀圆球体，忽略地球自转影响，根据HGV受力情况，在半速度坐标系(Velocity Turn Climb, VTC)中描述HGV的6自由度运动方程为[14]

2.2 HGV约束条件分析

HGV在机动过程中，为了满足任务要求和保持飞行器安全可靠飞行，通常需要满足一些约束条件，这些约束主要包括过程约束和终端状态约束[15]。

过程约束是指HGV在飞行过程中需要满足飞行器控制能力、防止结构性破坏和热烧蚀等，必须在可承受的最大热流密度、最大动压和最大过载下进行机动，才能保证机体安全性和可靠性。过程约束可表示为

其中，Kn为 常数，g0为海平面地球引力加速度。

终端约束是指HGV为完成任务、到达指定目标点所需要满足的状态约束，主要包括高度约束、速度约束、方位角约束等。设目标点位置坐标为(xt,yt,zt)， HGV滑翔段结束位置状态坐标为(xa,ya,za)， 速度为Va， 方位角为σa，则终端约束可表示为

2.3 HGV控制参数建模

HGV具有较强的机动性，即可以进行纵向机动，也可以进行横向机动。通过将两个方向的机动进行叠加，可以实现更为复杂的机动，以增加HGV轨迹灵活性，进而规避探测和禁飞区，提高突防成功概率。

2.3.1 纵向弹道控制参数建模

HGV在纵向上的机动主要有两种：平衡滑翔和跳跃滑翔。平衡滑翔条件下，飞行器纵向方向的受力达到平衡，速度倾角变化率为0，即θ˙ =0。由飞行器运动方程可知，其平衡滑翔条件下的控制参数模型应满足[16]

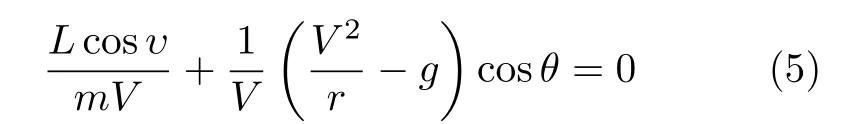
此外，HGV纵向上所受的气动力主要受攻角的影响，攻角的变化会带来HGV纵向所受气动力的变化。因此，平衡滑翔过程中，攻角应该始终保持不变。同时满足速度倾角变化率为0和攻角保持不变这两个条件，HGV才可以在纵向上实现平衡滑翔。

只要不满足平衡滑翔条件，HGV在纵向上就表现为跳跃滑翔的状态。通过控制攻角的变化，可以实现HGV在纵向上跳跃幅度、跳跃频率的变化。考虑到HGV在初始滑翔段由于速度较大，气动热是影响飞行的主要约束，应该采用较大攻角以提高飞行器下降时最低点的高度。而随着飞行器速度的降低，气动热不再是主要约束条件，此时为了增加航程，应该尽可能通过调整攻角，提高升阻比，让飞行器飞得更远。据此，将攻角建模为关于速度的函数

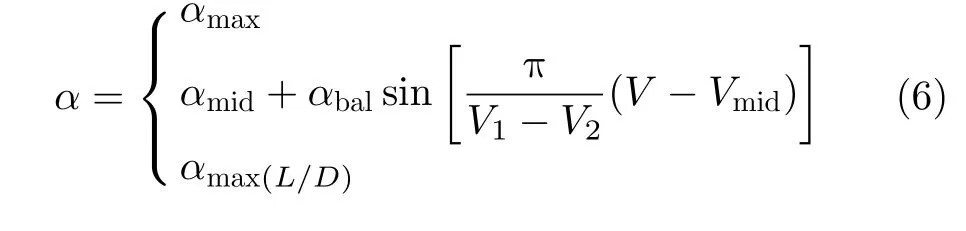
其中，αmax和αmax(L/D)分别为最大攻角和最大升阻比攻角，αmid=(αmax+αmax(L/D))/2，αbal=(αmax−αmax(L/D))/2，Vmid=(V1+V2)/2，L/D为升阻比。

2.3.2 横向弹道控制参数建模

HGV为了提升攻防能力，可以进行多种样式的横向机动，主要包括：无机动、C形机动、S形机动等。横向机动的实现主要受倾侧角的影响。

横向无机动可以降低飞行器设计难度，减少飞行器能量消耗，增加航程，但同时也会增加飞行器被拦截的概率。当HGV横向无机动时，倾侧角通常设为0。C形机动一般指左转弯或右转弯，其弹道较为稳定，机动样式较为单一。当HGV进行C形机动时，倾侧角通常设为常数，不翻转或只进行一次符号翻转。S形机动主要通过不断进行左右转弯实现，可以增加飞行器机动性能。当HGV进行S形机动时，倾侧角要通过方位角控制进行多次符号翻转，其控制参数模型为

3 HGV机动类别划分

3.1 机动类别

通过设计弹道控制参数，HGV可以在空中实现多种复杂机动。根据运动分解方法，可以将HGV空中机动在纵向平面和横向平面进行分解。HGV在纵向平面上的机动可以分为平衡滑翔和跳跃滑翔，在横向平面上的机动可以分为无机动、左转弯、右转弯和蛇形机动。通过将HGV纵向机动动作和横向机动动作进行合成，可以得到8个机动类别，分别对应8个机动动作标签，如图1所示。

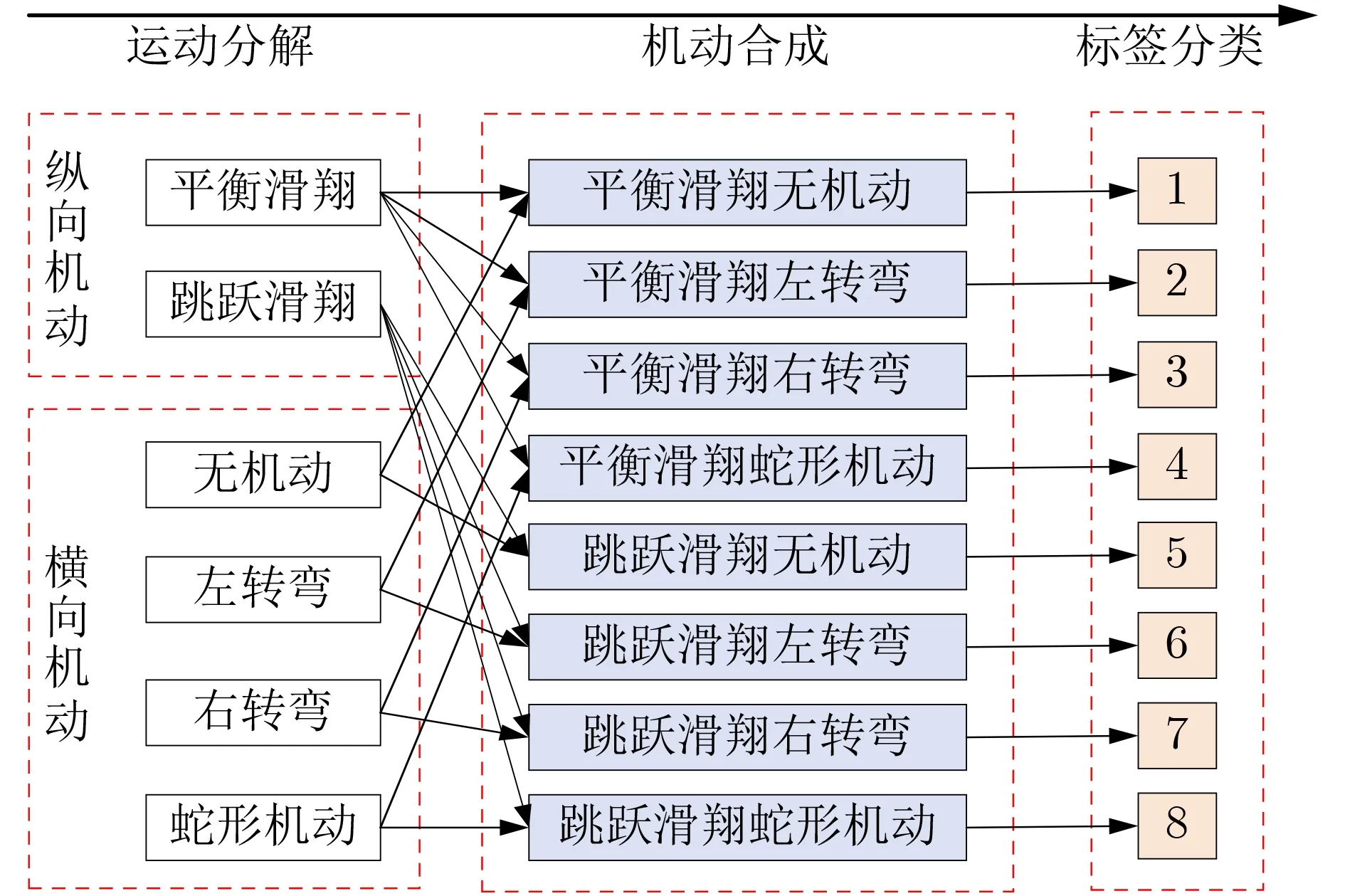
图1 HGV机动动作分类

3.2 特征识别参数构造与选取

根据飞行动力学相关知识[17]，HGV机动过程中伴随着各参数的变化，主要包括以下5个参数：高度h、高度变化率∆h、速度倾角θ、速度方位角σ、速度方位角变化率∆σ。 其中，高度h、高度变化率 ∆h和 速度倾角θ这3个参数主要对HGV纵向上的机动动作比较敏感，速度方位角σ和速度方位角变化率∆σ这2个参数主要对HGV横向上的机动动作比较敏感。

高度h是指HGV机动过程中质心与地面的垂直距离。高度变化率可以通过差分方法获取，公式为

当HGV纵向上平衡滑翔时，高度和高度变化率呈平稳变化，速度倾角接近零值；当HGV纵向上跳跃滑翔时，高度、高度变化率和速度倾角均呈规律性震荡。当HGV横向上无机动时，速度方位角保持不变，速度方位角变化率基本为0；当HGV横向上左转时，速度方位角不断减小，速度方位角变化率为负值；当HGV右转时，速度方位角不断增大，速度方位角变化率为正值；当HGV蛇形机动时，速度方位角和速度方位角变化率呈震荡变化。据此，可以分析出HGV机动状态和特征识别参数之间的映射关系。HGV机动状态识别实际上就是先建立机动状态和特征识别参数之间的映射关系，然后通过状态识别方法捕捉特征识别参数的变化，进而对应到机动状态，从而完成了HGV机动状态的识别。

3.3 轨迹库生成

通过设计不同初始变量条件和不同控制参数模型，利用式(1)–式(7)，可以生成HGV不同机动状态下的机动轨迹。本文共仿真生成了2430条轨迹，4.374×106个轨迹点，包含了HGV的各类机动模式，形成HGV轨迹库。

4 雷达跟踪与特征提取

设地球半径为Re，雷达站所处位置的高度为H0， 地理经度为λ0，地理纬度为φ0，通过雷达跟踪得到的HGV状态信息为 (x～k,y～k,z～k,v～xk,v～yk,v～zk)，其中下标x, y, z表示3个坐标轴，上标“～”表示估计，下标k表示时刻。速度信息可通过位置进行差分得到。雷达跟踪获得的HGV状态信息是建立在雷达东北天(East North Up, ENU)坐标系中的。而HGV机动状态识别需要获取飞行器的高度、高度变化率、速度倾角、速度方位角和速度方位角变化率。因此，需要通过坐标转换将雷达ENU坐标系下的跟踪信息转换为HGV特征识别参数信息。主要通过以下3个步骤实现：

步骤1 将HGV在雷达ENU坐标系中的跟踪信息转换到地心(Earth-Centered, EC)坐标系。

高度变化率可以通过高度信息进行差分得到。

步骤2 将HGV在EC坐标系下的速度信息转换到飞行器ENU坐标系。

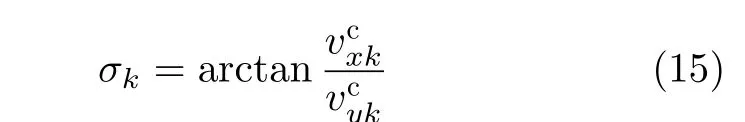
速度方位角变化率可以通过速度方位角进行差分得到。至此，通过式(9)–式(15)，可以完成雷达跟踪信息的实时转换，得到所需的特征识别参数信息。

5 机动状态识别方法

5.1 数据处理

对HGV机动特征识别参数信息进行提取后，首先通过移动平均法对数据进行平滑处理以尽量消除跟踪噪声的影响。然后，为便于模型学习数据规律和特点，将平滑后的数据进行归一化，采用最大最小法将每个维度的特征识别参数归一化到[–1,1]区间。最后，对3.1节划分的8个机动类别标签进行独热编码(One-Hot)。

5.2 AT-ConvLSTM模型

本文所构造的机动特征识别参数是一个多维时间序列数据，能够比较完整地反映HGV空间机动特征，兼具了时间特性和空间特性。考虑卷积神经网络(Convolutional Neural Networks, CNN)在局部特征提取方面的优势和长短时记忆网络(Long-Short Term Memory Network, LSTM)在时间序列处理方面的优势，设计了一种基于AT-ConvLSTM的状态识别方法。

CNN是一种仿造生物视觉神经机制构造的神经网络[19]，通过卷积核进行卷积操作获取“感受野”范围内的数据关系特征，具有权值共享和局部感受野的优势，能够很好地提取局部特征[20]。LSTM是1997年由Hochreiter和Schmidhuber提出的[21]，在循环神经网络(Recurrent Neural Network,RNN)的基础上增加了一个新的状态，称为单元状态ct，并通过引入3个门：输入门、输出门和遗忘门，解决了RNN存在的梯度消失或梯度爆炸问题[22]。在前向传播过程中，输入门ft决定了当前时刻的单元状态ct可 以保留多少当前时刻的输入xt；输出门ot决 定了当前时刻的单元状态ct有多少可以传送到输出ht；遗忘门it决 定了当前时刻的单元状态ct可以保留多少上一时刻单元状态ct−1的信息。

ConvLSTM是2015年由Shi等人[23]提出的，结合了LSTM和CNN两种模型的优势，其主要改进之处是用卷积运算代替了LSTM中当前输入和短期记忆结合后的矩阵乘法运算，因此可以更好地对时间序列信息的特征和规律进行提取，已经在时间序列分类和预测等领域得到了广泛关注。其具体计算过程为

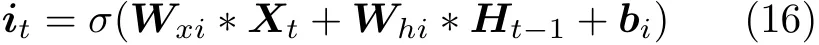
受人类视觉系统处理信息时可以自动抓取关键信息的启发，注意力机制可以通过调整信息的概率分配来增加重要信息的影响，减弱非重要信息的影响，在语音识别、机器翻译等方面获得了广泛关注[24]。这里，由于HGV机动状态识别的输入信息是多维的时序数据，添加注意力机制有利于提高关键特征信息的影响，有利于模型抓取状态识别的重要特征。因此，本文在ConvLSTM层后添加注意力机制。假设有k个特征向量输入，则第i个特征向量的得分计算公式为

最后，添加全连接层，并通过softmax激活函数对HGV机动状态进行分类，得到每个机动状态对应的概率，最大概率对应的机动状态即为网络输出的HGV机动状态。计算公式为

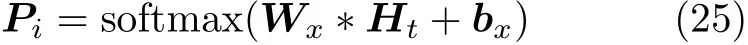
其中，Wx和bx分别为softmax层对应的权重和偏置。

6 仿真验证

6.1 网络训练

选择自适应矩估计(Adaptive moment estimation, Adam)优化器作为优化方法，根据误差梯度对模型中的参数进行优化。Adam是对传统随机梯度下降算法的扩展，不仅能计算模型中各参数的自适应学习率，还可以使模型更高效地收敛。选择交叉熵作为损失函数，可以根据误差的大小调节权重更新速度。本文将轨迹库中80%的数据作为训练数据，20%的数据作为验证数据。同时，为降低过拟合风险，在模型中添加了L2正则化和Dropout层。

本文设计的识别网络模型结构共有5层，包括2层ConvLSTM层、1层Dropout层和2层全连接层。模型学习率设计为0.001。训练次数和批量大小分别设计为100和128。模型输入的数据是一个5维的时间序列，采样间隔为0.5 s。模型的输出是一个二进制的one-hot向量。实验在处理器为Intel Core i7-10510U、内存为16 GB、操作系统为Microsoft Windows 10(64位)的移动工作站进行。本文模型代码通过Python 3.7.6版本编写，基于TensorFlow框架实现。

6.1.1 时间步长设计

时间步长是影响模型性能的一个重要指标，时间步长的大小直接影响模型的识别精度和收敛速度。选取合适的时间步长有利于改善模型的识别能力。将学习率设为0.001，以50为间隔，在50到300的范围内对时间步长进行等间距实验，对不同时间步长下网络模型的识别精度和收敛性进行分析。训练结果如表1所示，损失曲线和准确率曲线如图2所示。

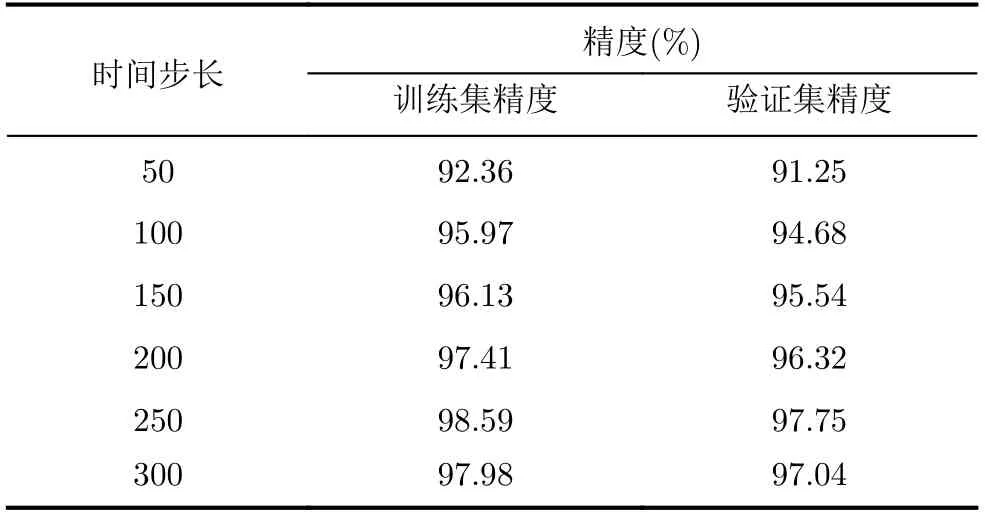
表1 不同步长对应的模型训练结果

从图2可以看出，在时间步长从50调整到300的过程中，准确率曲线先上升后下降，损失曲线先降低再增大。当时间步长为250时，准确率达到最高，损失达到最小。这可能是因为，HGV的机动状态变换需要一个时间过程，当时间步长逐渐增大时，时间周期变长，积累了更多机动状态信息，有利于模型正确判断HGV所处的机动状态。但当时间步长过大时，可能会造成一定的过拟合现象，一定程度上抑制了模型的性能。因此，本文将时间步长设置为250。

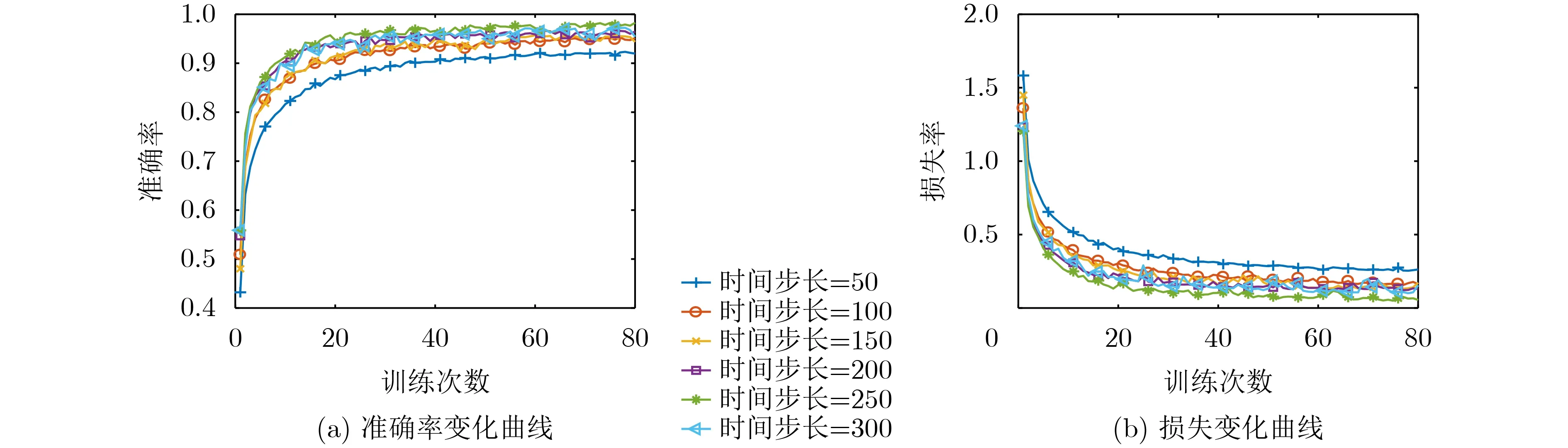
图2 模型的准确率和损失变化曲线

6.1.2 模型对比

选择RNN模型、LSTM模型、CNN-LSTM模型和ConvLSTM模型作为对比模型，时间步长和学习率的设置与AT-ConvLSTM相同。利用轨迹库中数据分别对几种深度学习模型进行训练，其训练具体结果如表2所示，损失曲线和准确率曲线如图3所示。

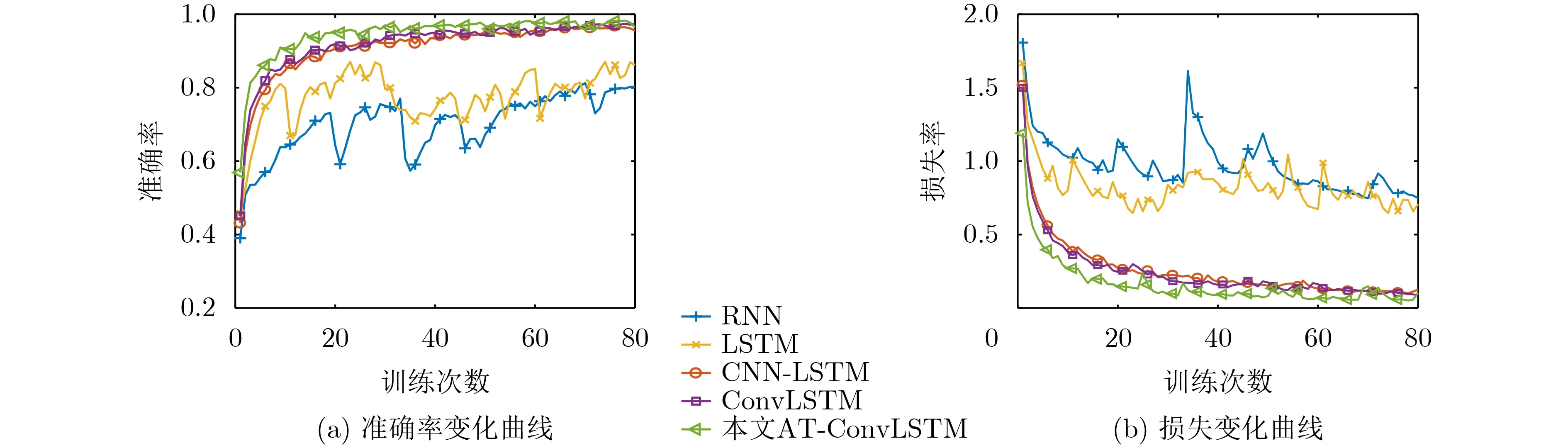
图3 不同模型的训练结果

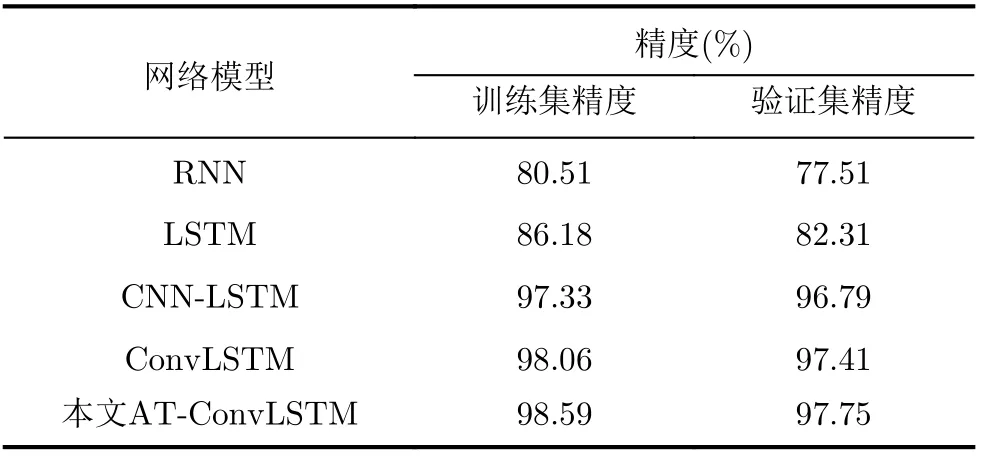
表2 模型精度对比

可以看出，RNN模型和LSTM模型的正确率曲线明显低于其他3种模型，说明RNN模型和LSTM模型虽然在处理长时依赖问题中具有优势，但在特征提取方面处于劣势，导致无法很好地进行HGV机动模式分类。CNN-LSTM模型、ConvLSTM模型和AT-ConvLSTM模型在训练集和验证集上都取得了较高的正确率。这是因为CNN-LSTM模型结合了CNN和LSTM的优势，擅于提取局部特征，ConvLSTM模型正确率略高于CNN-LSTM模型，是因为CNN-LSTM模型先将信息输入卷积层，再输入LSTM层，相当于对数据中的空间特征和时间特征进行了分开处理，而ConvLSTM模型将卷积运算嵌入了LSTM层，同时处理了数据中的时间和空间特征。但综合对比之下，AT-ConvLSTM模型由于在ConvLSTM模型的基础上又添加了注意力机制，能够更好地获取关键特征，所以识别正确率最高、效果最好。

6.2 机动状态在线识别

6.2.1 典型样本下模型性能测试

为验证模型对典型样本的识别性能，设计了两条典型HGV机动轨迹，如图4所示。其中，轨迹1机动状态为平衡滑翔右转弯，轨迹2机动状态为跳跃滑翔无机动。雷达的参数设置如下：距离误差为200 m，方位角误差为0.1º，俯仰角误差为0.1º，采样率为0.5 s。利用文献[14]中的方法对轨迹进行实时跟踪，得到HGV机动状态信息。

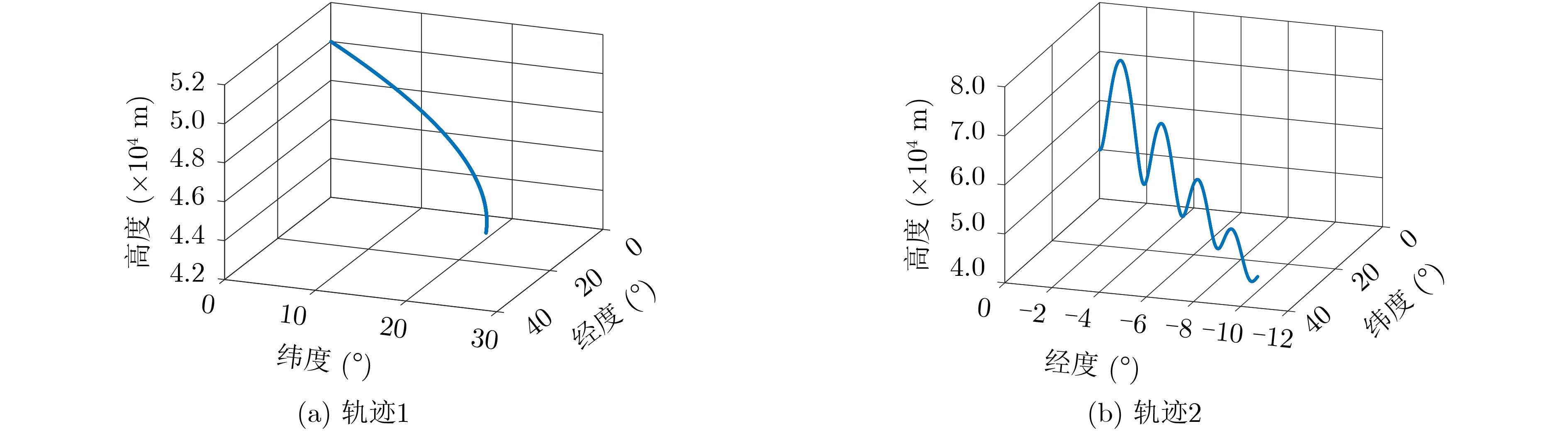
图4 典型HGV轨迹

通过第4节的方法将雷达跟踪到的HGV状态信息转换为特征识别参数信息，然后利用训练好的ATConvLSTM网络模型对跟踪到的HGV轨迹进行在线识别，并与其他模型进行对比，验证算法的实用性。

分别利用不同模型对两条HGV轨迹进行在线机动状态识别，对各模型的识别准确率进行计算，结果如表3所示。可以看出，各模型在对轨迹1的识别中都取得了较好的效果，但是在对轨迹2的识别中，LSTM模型和RNN模型的准确率都明显降低。分析其原因，可能是由于轨迹2相对轨迹1机动性更强，特征参量变化较大，导致LSTM模型和RNN模型无法较好提取特征信息，从而降低了识别准确率。还可以发现本文提出的基于AT-ConvLSTM的机动状态识别模型在对不同机动状态的HGV轨迹识别中始终保持了稳定的性能，相比其他模型具有更好的准确率。

表3 模型识别结果

6.2.2 多样本下模型性能测试

为了对模型的性能进行更为全面的衡量和测试，在6.2.1节基础上，增加样本数量，在多样本下进一步分析模型性能。

在不同初始条件下生成24条包含各类机动状态的HGV轨迹(每种机动状态对应3条)，共计43200个轨迹点，利用文献[14]中的方法对轨迹进行实时跟踪，得到HGV机动状态信息。雷达跟踪参数和特征参数提取方法同6.2.1节。然后利用训练好的ATConvLSTM网络模型对跟踪到的HGV轨迹进行在线识别，并与其他模型进行对比，验证算法的实用性。

分别利用不同模型对HGV轨迹进行识别，准确率结果如表4所示。可以看出，由于跟踪噪声的影响，所有模型的识别准确率相比训练集和验证集都有所下降，但仍保持了一定精度。本文所提模型的准确率为92.36%，优于其他模型。识别准确率堆叠直方图如图5所示，图中将HGV不同机动类别的识别点数占总点数的比例进行堆叠，可以看出，平衡滑翔模式下的机动类型1的识别准确率普遍偏低。分析其原因，可能是机动类型1属于平衡滑翔无机动模式，HGV轨迹相对更为平稳，各特征识别参数的变化也较为平稳，变化不够明显，同时受到噪声干扰，因此导致机动类型1的识别相对困难。

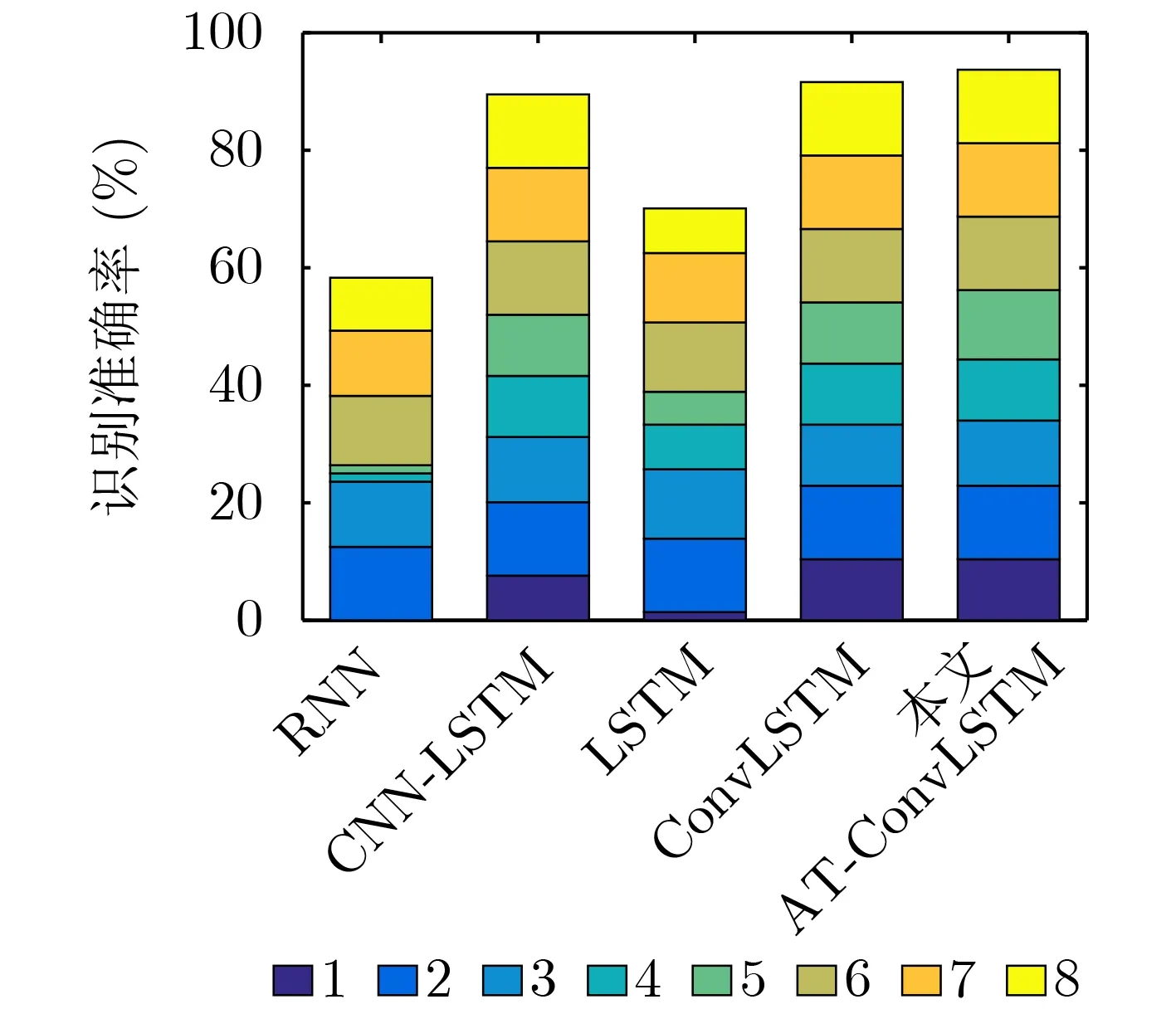
图5 识别准确率堆叠直方图

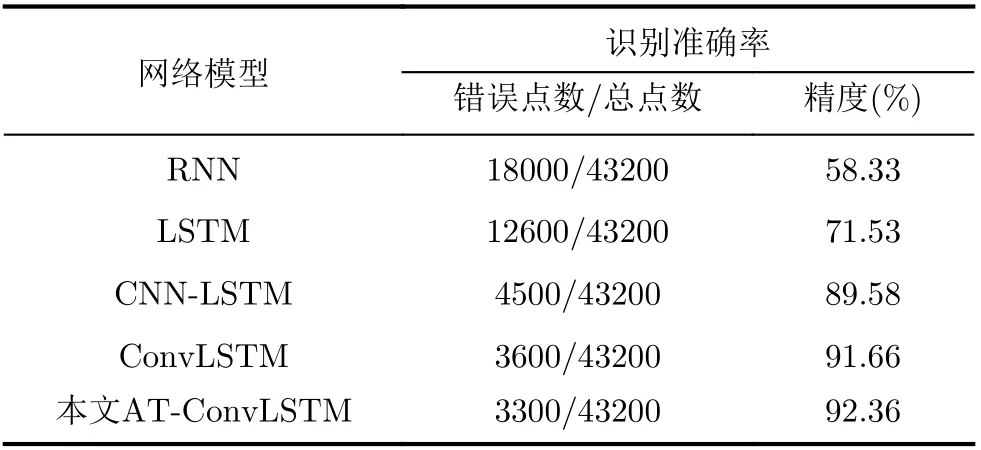
表4 模型识别准确率结果

计算不同模型单次机动识别的平均耗时，结果如图6所示。可以看出，模型识别耗时普遍较低，均小于0.1 s。其中本文模型的平均耗时为0.0577 s，可以满足实时性要求，能够进行机动状态在线识别。

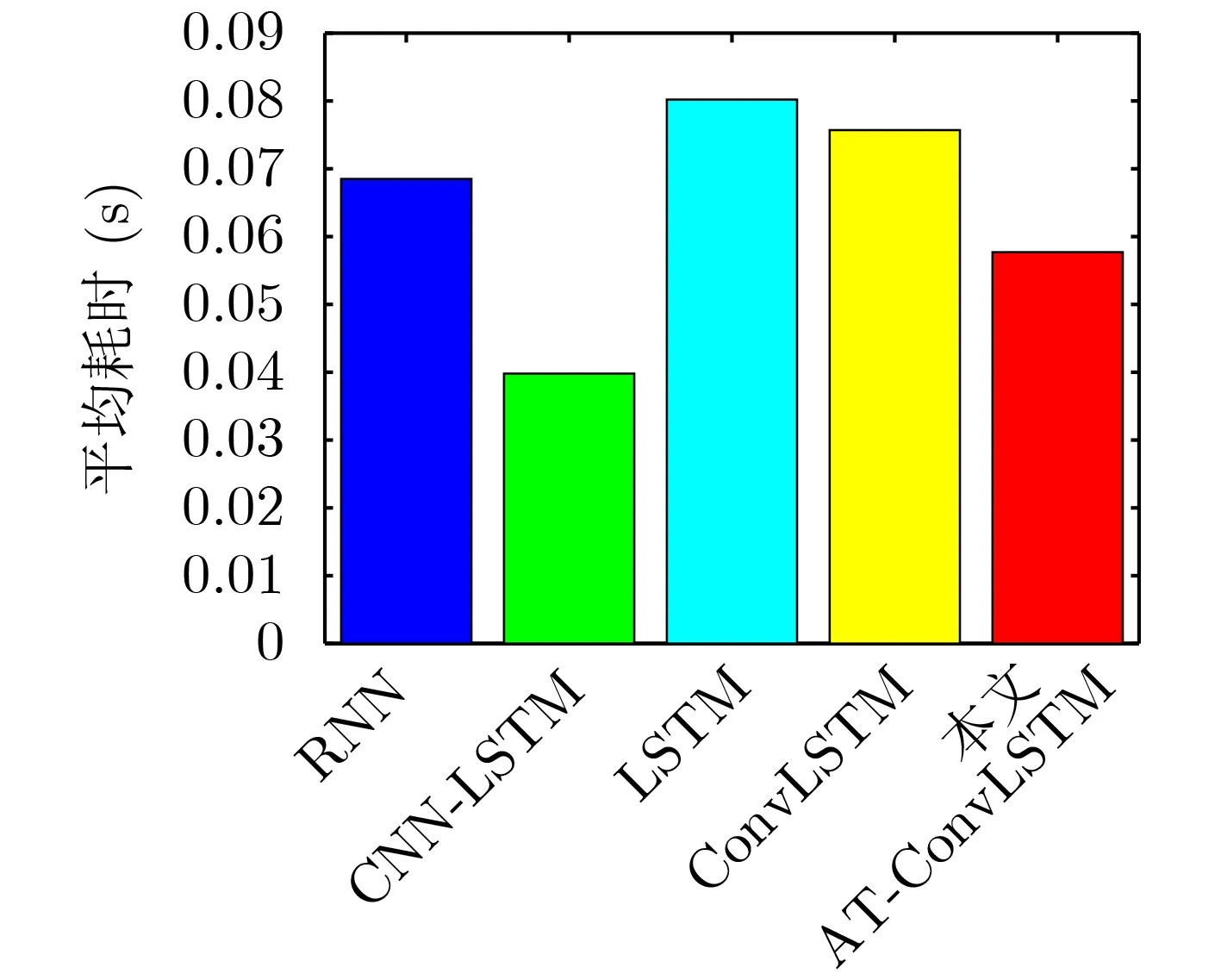
图6 不同模型的平均耗时

7 结束语

本文利用深度学习理论对HGV机动状态识别进行研究，首先建立了HGV机动模型，对机动控制参数进行了分析，根据HGV横向和纵向机动特点，将机动类别划分为8类，然后，推导了从雷达跟踪到特征识别参数的转换步骤，实现了特征参数的提取，最后，通过训练AT-ConvLSTM网络对HGV机动状态进行在线识别。通过分析可以得到以下结论：

(1)本文模型可以较好地处理多维度的时间序列信息，利用卷积长短时记忆网络在时空数据处理方面的优势和注意力机制对关键特征提取方面的优势，在HGV机动状态识别中取得了较高的准确率；

(2)本文模型具有较好的鲁棒性，不仅在训练集和验证集中取得了较好的结果，在对雷达跟踪的HGV轨迹数据进行识别时，也能够较好地应对跟踪噪声的污染，保持良好的性能；

(3)本文模型可以对HGV机动状态进行在线有效识别。模型在训练集和验证集中分别取得了98.79%和97.95%精度，在对多轨迹样本的识别中取得了92.36%的精度，与其他几种模型相比，性能更好，且耗时较短，能够满足在线识别的要求。