应力偶流体润滑轴承油膜压力和轴心轨迹计算

马艳艳

(上海理工大学中德学院 上海 200093)

精确预测轴承的性能，对提高内燃机的寿命及可靠性有非常重要的意义，而轴承的润滑状况决定了它的工作可靠性和使用寿命[1]。在实际工况下，为保证轴承润滑良好，需改善润滑油的使用性能，这通常要在润滑油中加入各种高分子聚合物添加剂。高分子聚合物的添加会使得流体的润滑具有非牛顿性，主要表现为存在应力偶效应[2]。应力偶流体是一种黏性介质，含有添加剂的润滑剂中悬浮着刚性的、随机排列的粒子，其主要特征是应力张量呈现非对称性，并且它们的流动行为不能用经典的牛顿理论来预测。如何运用合适的理论模型分析应力偶润滑的现象是现在润滑理论研究的前沿课题之一。STOKES首先建立了应力偶流体的本构方程[3]。近年来，应力偶模型在轴承的静态特性和纯挤压特性方面有很多研究。LIN等[4-5]对有限长滑动轴承的应力偶流体润滑性能进行了研究。NADUVINAMANI等[6-7]对应力偶流体润滑的多孔短轴承及表面粗糙度对转子轴承的静态特性的影响进行了研究。朱军超等[8]考虑应力偶计入区间及黏压效应进行了倾斜轴承非牛顿流体润滑特性研究。王晓力和朱克勤[9]对计入应力偶效应和空化效应的滑动轴承热流体动力润滑进行了数值研究。张俊岩和王晓力[10]基于质量守恒边界条件对应力偶流体润滑的动载轴承特性进行了研究。本文作者在之前的研究中针对应力偶流体润滑动载滑动轴承性能的影响因素进行了分析，研究了不同的动力参数、弹性系数与应力偶参数对轴承中截面的周向油膜压力分布的影响[11-13]。上述文献均没有对应力偶流体润滑轴承进行轴心轨迹的计算研究。

轴心轨迹可给出轴承在工作时任意时刻的油膜形状，确定轴承的润滑情况，也是判断轴瓦失效的基础。因此，无论是对轴承的设计，还是对轴承失效进行分析与鉴别，求出它的轴心轨迹都具有非常重要的意义。目前针对轴心轨迹的研究较少[14-15]。高明和龙劲松[14]研究了动载滑动轴承的轴心轨迹计算机模拟中Holland方法的改进。卢耀辉等[15]基于ADAMS/ENGINE计算得到了不同转速下，不同轴承间隙及油孔供油或油槽供油条件下的轴心轨迹，为滑动轴承设计提供数据支持。

轴承的润滑状况是预测其性能的重要因素，而对轴承润滑状况进行分析的最基本和重要的计算，是轴承油膜压力分布和轴心轨迹的计算[2]。本文作者根据前期研究推导的应力偶流体动态润滑轴承雷诺方程，分别计算和分析了某柴油机轴承采用牛顿流体和非牛顿应力偶流体润滑时的油膜压力分布和轴心轨迹，对轴承的设计和轴承失效的分析与鉴别具有非常重要的意义。

1 数学模型

1.1 轴承应力偶流体Reynolds方程及边界条件

轴承的物理模型如图1所示，直角坐标系(x,y,z)和柱坐标系(r,ψ,z)固定连接于轴承，坐标原点位于轴承宽度中点且与轴承中心处重合，φ为偏位线OjOb的方位角，Rj为轴颈半径，Rb为轴承内径，c=Rb-Rj，e为偏心距，ε=e/c，ε为偏心率，φ为承载力作用角，W为量纲一油膜承载力。在动载荷的工作情况下，载荷的大小和方向都是变化的，因而轴颈和轴承的角速度ωj和ωb也是变化的[11]。

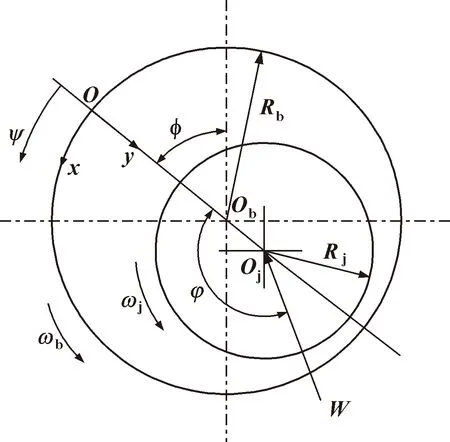
图1 轴承几何模型

与轴颈尺寸相比，润滑油膜厚度很小，不计及体力和体力矩时，根据不可压缩应力偶流体的动量方程和连续性方程可得应力偶流体在x和z方向上的速度分量[2]，将其代入连续性方程并沿着油膜厚度方向积分，可得动态工况下应力偶流体润滑轴承Reynolds方程[12]为

(1)

式中:h=c+ecosψ;f(h,l)=h3-12l2[h-2ltanh(h/(2l))];Uj=Rjωj≈Rbωj;Ub=Rbωb;t为时间;p为压力;l为应力偶参数，当l=0时为牛顿流体。

则应力偶流体润滑条件下适用于动态润滑轴承的变形量纲一化Reynolds方程为

-εsinψ+qcosψ

(2)

式中：h′=1+εcosψ

f′(h′,l′)=h′3-12l′2[h′-2l′tanh(h′/2l′)]

由轴承的状况，其解具有对称性和周期性。在方程数值求解过程中，采用负值充零算法来设定油膜压力边界条件。假设轴承的周向ψ*处为气蚀区开始处，则压力边界条件为

(3)

1.2 轴心轨迹计算

轴颈的运动轨迹称为轴心轨迹。轴承是否有承载油膜或油膜厚度是否足够大，并不是简单地决定于轴承载荷、轴颈及轴承速度v是否够大，而需要根据润滑理论算出轴心轨迹才能判别。动载滑动轴承因为油膜的动压受到旋转和挤压效应的共同作用，它的轴心轨迹是变化的。在正常的工作条件下，轴承的轴心轨迹收敛于固定的曲线。

最具有代表性的计算动载轴承轴心轨迹的算法有3种：Holland的承载力矢量叠加法、Hahn的压力叠加法和Booker的迁移率法[14-15]。根据研究对象的实际工作特点，为了克服动载滑动轴承雷诺方程求数学通解的困难，可采用Holland法计算。求出轴承的油膜压力分布后，采用如图2所示的计算步骤分析轴承的轴心轨迹变化。

图2 轴心轨迹计算流程

2 数值求解方法

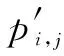
(4)

图3 求解区域的节点划分

对任意给定的初始条件，用周期性条件完成动载问题的求解。

(5)

若T≤1.0×10-3，则迭代过程终止。

3 计算结果与分析

以某型柴油机滑动轴承为例，当采用应力偶流体润滑时，进行了油膜压力分布和轴心轨迹计算。轴承的具体工况与几何参数如表1所示。

表1 轴承工况与几何参数

3.1 油膜压力

针对某型柴油机轴承的计算得到某一时刻不同的应力偶参数对轴承油膜压力分布的影响如图4所示，图中p′为量纲一油膜压力。可以看出，与牛顿流体(l′=0)相比，非牛顿性应力偶流体润滑时轴承的油膜压力增大，当应力偶参数分别为l′=0.1、l′=0.2和l′=0.3时，最大的量纲一油膜压力分别增加了49.33%、198.55%和444.78%(如表2所示)。上述数值分析结果表明，l′=0时油膜压力最小，随着l′的增大，油膜压力明显提高。应力偶流体与牛顿流体相比油膜压力增加，应力偶参数越大，最大油膜压力越大，应力偶效应越显著，且随应力偶参数的增加，最大油膜压力的值在ψ增大的方向。

图4 不同应力偶参数对轴承油膜压力分布的影响

表2 不同应力偶参数下轴承油膜压力

3.2 轴心轨迹

某型柴油机轴承负荷图如图5所示，计算所得的轴心轨迹如图6所示，可见，在一个载荷变化周期中，空穴的位置随时间变化。轴心轨迹的形状在牛顿流体和应力偶流体2种润滑条件下非常相似，区别在于l′=0时轴心轨迹偏离轴承中心较远，而l′=0.2时轴心轨迹向其中心靠近。l′=0时轴承的最小油膜厚度为1.995×10-2mm，而l′=0.2时轴承的最小油膜厚度为2.559 8×10-2mm，其在轴心轨迹图上对应的轴承角度为-105.7°。这表明在润滑油中加入高分子添加剂后，增大了油膜厚度，改善了轴心轨迹。

图5 轴承负荷

图6 轴承的轴心轨迹

4 结论

根据应力偶流体动态润滑轴承Reynolds方程，用数值计算的方法比较研究了不同应力偶参数对动载滑动轴承润滑性能的影响。针对某柴油机轴承，采用牛顿流体和非牛顿应力偶流体润滑时的工作情况分别进行了油膜压力分布计算和轴心轨迹计算。结果表明：

(1)非牛顿应力偶流体和牛顿流体相比较，增加了油膜压力，轴承的承载能力提高，并且应力偶参数值越大，其油膜压力也越大，应力偶效应越显著，且随着应力偶参数增加，最大油膜压力的值出现在轴承角度ψ增大的方向。

(2)牛顿流体和非牛顿应力偶流体润滑条件下，轴心轨迹形状十分相似，不同之处是牛顿流体润滑条件下的轴心轨迹偏离其中心较远，而应力偶流体润滑条件下轴心轨迹向轴承中心靠近。

(3)润滑油中加入高分子添加剂后，增大了油膜厚度，改善了轴心轨迹，从而提高了轴承的润滑性能。这无论是对轴承的设计，还是对轴承失效进行分析与鉴别都具有非常重要的意义。