风电接入系统的电压越限薄弱节点综合识别

李梦珊，蔺 红，张 良，祁世琛

(1.新疆大学电气工程学院，新疆 乌鲁木齐 830017；2.国网新疆电力有限公司电力科学研究院，新疆 乌鲁木齐 830001；3.国网新疆电力有限公司乌鲁木齐供电公司，新疆 乌鲁木齐 830000)

0 引 言

随着风电并网规模的不断增大，电力系统的不确定性逐步加强，其运行状态愈加逼近临界点[1]。大规模风电并网，时变随机的风电、负荷功率会导致电压波动，电压越限问题日益突出，如果电网发生扰动，可能在薄弱节点处首先出现电压问题进而波及到整个地区[2]。因此，研究适用于风电接入系统的电压越限薄弱节点可靠识别方法十分必要。

电力系统众多电压薄弱节点判定指标中，负荷裕度蕴含大量信息、准确性强，引发学者持续关注。从系统自身来看，充裕的负荷裕度是电压安全运行的重要保障[3]。然而计算负荷裕度的传统方法受限于PV曲线的制取速率，为此学者开展大量研究[4-7]。文献[4]采用快速解耦法改善连续潮流法的校正阶段。文献[5]借助Levenberg-Marquardt算法将传统连续潮流法进行改进。文献[6]引入并行计算硬件技术提升直接法计算负荷裕度的效率。文献[7]基于梯度提升决策树建立离线运行点数据库以实现负荷裕度的在线计算评估。

然而以上关于负荷裕度的研究仍基于特定功率转移方式，难以适用于强不确定性的大规模风电接入系统。电力系统安全域方法理论体系不断完善[8-11]，给这一问题带来新的思路。静态电压安全域(SVCR)描述了电力系统在确定拓扑及参数下的静态电压安全运行区域，可直观、全面评估系统在不确定因素影响下的电压安全性，其边界计算是重要问题。目前常用的边界计算方法有拟合法和超平面近似法[12]。拟合法搜索足量临界点拟合为边界，局限于降维空间，丢失了大量重要信息。超平面近似法用超平面描述边界，结果仍是高维空间的，且其线性特性利于应用，基于这样的SVCR考察电压安全裕度，在离线计算节点SVCR边界的基础上，可快速辨识电压安全性弱的节点，但目前对这方面的研究较少。

此外，节点的电压安全不仅与系统安全性能密切相关，还需考虑风电功率不确定性的影响。文献[13-14]指出电压薄弱节点识别不仅要关注节点自身抗扰动能力，还要考虑所承受的扰动影响程度。风电接入系统的显著特征是风电功率的不确定性强，因而电压薄弱节点的评估应考虑系统自身和风电场两个方面的因素。

基于上述考虑，开展以下研究。首先，借助拉格朗日乘数法，快速计算节点电压限值临界点及SVCR边界，获得有向电压安全裕度，用以判别节点电压安全状态、强弱。其次，利用熵值法确定无功-电压灵敏度的权重并计算总灵敏度，用于识别对风电场节点无功敏感的节点。然后，结合电压安全裕度和无功-电压灵敏度制定了电压薄弱节点综合识别方法，用于电压安全分析和调控策略制定。最后的仿真算例验证了所提方法的可行性和有效性。

1 基于SVCR的电压安全裕度

1.1 基于SVCR的电压安全裕度

电力系统节点电压与实时控制的决策变量息息相关。为描述系统节点电压与各决策变量的关系，基于传统P-V曲线，定义多维空间决策变量-电压(D-V)曲线族和基于SVCR的节点电压安全裕度。

图1 基于SVCR的电压安全裕度示意

分析实际电力系统时，安全裕度是高维空间的，反映多维决策变量的影响。该指标的应用依赖于决策空间SVCR边界，因而边界的计算十分重要。

1.2 SVCR边界计算

1.2.1 风电接入系统的SVCR

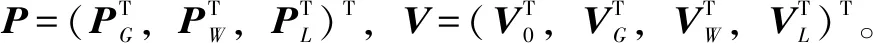
(1)

风电接入系统SVCR是决策空间上满足潮流约束及节点电压安全约束的运行点的集合ΩV

(2)

式中，f(x，y)=0为潮流等式约束；RV为节点电压幅值不等式约束。

图2 系统SVCR示意

1.2.2 节点SVCR边界计算

风电场和负荷节点属于PQ节点，引用文献[12]方法，基于交流潮流模型并结合电压安全约束进行推导，边界格式为

(3)

(4)

发电机节点是PV节点，SVCR边界由电压限值直接确定

(5)

将式(5)整理为式(3)形式，如式(6)所示，其边界系数向量除对应该节点电压幅值的位置外其余元素为0，如式(7)所示。

(6)

(7)

1.2.3 计算临界点

临界点可通过构建以满足特定安全约束条件下裕度最大为目标的优化模型求解，是仅含等式约束的寻优问题。拉格朗日乘数法可将这种问题转化为一组非线性方程，求解繁冗程度骤减。因此，引入拉格朗日乘数法加速临界点计算过程。

计算节点i电压限值临界点的优化模型为

(8)

对于式(8)构造拉格朗日函数

(9)

式中，λ=[λ1，λ2，…，λn+1]；u为拉格朗日乘数。

依据拉格朗日乘数法，令拉格朗日函数对所有变量、乘数的偏导数为0，得到一组非线性方程，可采用牛顿法迭代计算，获得临界点。

1.3 有向电压安全裕度的计算及应用

(10)

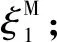
(11)

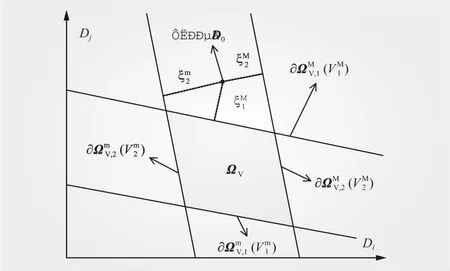
图3 节点电压越限或安全示意

2 风电场无功-电压灵敏度

2.1 无功-电压灵敏度

对牛顿法修正方程求逆可得

(12)

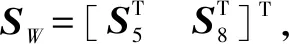
2.2 熵值法确定多风电场灵敏度权重

系统中含有多个风电场时，需要指定各个风电场无功-电压灵敏度的权重。熵值法是一种客观的权重确定方法，用于确定风电场无功-电压灵敏度权重的步骤如下：

(1)选取样本对象为n-g个负荷节点，样本指标为w个风电场无功-电压灵敏度，xij为第i个节点的第j个风电场无功-电压灵敏度的数值∂Vi/∂Qj(i=1，2，…，n-g;j=1，2，…，w)。

(2)对样本指标归一化处理

(13)

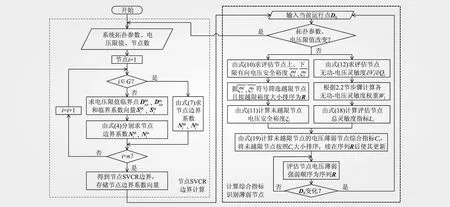
图4 电压薄弱节点综合识别方法流程

式中，zij为第i个节点的第j个风电场无功-电压灵敏度归一化指标。

(3)计算第j个风电场无功-电压灵敏度下第i个节点所占比重pij

(14)

(4)计算第j个风电场无功-电压灵敏度的熵值ej

(15)

式中，k=1/ln(n-g)>0。

(5)计算信息熵冗余度dj

dj=1-ej

(16)

(6)计算各个风电场无功-电压灵敏度权重Wj，如式(17)所示；显然，当系统中仅含一个风电场时，其对应的无功-电压灵敏度权重为1。

(17)

熵值法确定权重后，节点i的总灵敏度为

(18)

3 电压薄弱节点综合识别方法

基于SVCR的电压安全裕度反映了系统安全性能即节点自身的抗扰动能力。节点的电压安全裕度越高，表明该节点抵御功率波动的能力越强，节点越安全。无功-电压灵敏度侧重于描述风电场与系统间无功、电压的交互作用。节点的无功-电压灵敏度越大，表明节点电压受风电不确定性的影响越大，节点越敏感。因此，对于大规模风电接入系统，提出电压薄弱节点综合指标Ci，该指标值越大，表明该节点越薄弱。

Ci=Li/ξi

(19)

结合上述指标，提出含风电系统的电压薄弱节点综合识别方法，流程如图4所示。SVCR与运行状态无关，节点SVCR边界计算部分完成后，将节点SVCR边界以边界系数向量表示并存储，若系统拓扑、参数不变，该部分无需重复计算，只需要输入新场景的运行点D0，进行后续计算识别流程。

4 算例分析

采用IEEE39节点系统进行仿真。假设同步机节点电压幅值恒定，因而评估节点为负荷节点1～29，其电压上、下限均设定为标幺值1.06、0.94。

4.1 电压安全裕度计算

4.1.1 节点SVCR边界及系统SVCR

设额定功率为100 MV·A，描述系统运行状态的运行点用标幺值表示。根据1.2节，计算各节点SVCR边界。算例对节点15设置不同场景，故以节点15的SVCR边界为例进行观察，而边界系数绝对值越大，对应的决策变量对节点电压的影响越大，因此，分别在节点15电压限值边界的决策变量P、VG、QL对应边界系数中选取几个绝对值较大的系数，如表1所示。

表1 节点15的SVCR边界系数(部分)

由表1可以看出，PQ节点无功系数绝对值远远大于有功系数绝对值，表明相较于有功功率，无功功率与电压幅值关系更为密切；PQ节点无功系数中，节点自身系数绝对值最大，表明节点自身无功功率变化对电压幅值的影响最大。这些规律都与实际电力系统相符，说明节点SVCR边界的有效性。

4.1.2 基于SVCR的电压安全裕度

根据1.3节方法计算各评估节点的有向电压上、下限安全裕度，根据符号判断出节点电压均未越限，数值结果如图5所示。

图5 各评估节点电压安全裕度

为验证节点电压安全裕度的有效性，将电压安全裕度计算结果与潮流计算结果进行对比。节点电压安全裕度的大小代表了该节点电压安全性的强弱，故将评估节点按照节点电压安全裕度的数值由小到大排序；然后使用PSASP软件进行潮流仿真计算，将各评估节点电压分别与电压上、下限值相减取绝对值，令两者中较小值作为该节点的电压偏差，电压偏差越小表示节点电压安全性越弱，将节点按照电压偏差由小到大排序。分别取排序前十项，两种方法结果对比如表2所示。

表2 电压安全裕度与潮流计算结果对比

由表2可以看出：电压安全裕度排序结果中，节点25数值极小，节点29、28、26、22、19数值相近，其次是节点2、23、1、9；潮流计算结果中，节点25数值极小，节点26、28、22、29、19数值相近，然后是节点2、23、1、27。两者排序结果相似，验证了电压安全裕度的有效性。

4.2 负荷、风电波动场景下仿真计算

4.2.1 负荷增加场景

为模拟负荷功率波动，令节点15负荷功率保持原功率因数(0.902 18)增长，运行点在SVCR的轨迹如图6所示。

图6 节点15负荷增长时的运行点变化轨迹

当负荷有功功率增加694 MW时，节点15电压下限安全裕度降低至0.000 114(<10-3，接近于0)，表明节点15电压濒临安全下限。对该极限状态用PSASP软件进行潮流仿真计算，可得节点15电压值降为0.940 21，与电压下限相对误差为0.02%，在允许误差范围内。

4.2.2 风电出力增加场景

为模拟风电功率波动，将节点15接入风电场(设功率因数为0.95滞后)，令其发电量逐渐增加。考虑系统电量平衡，相应减少节点39同步机出力直至0。节点15风电增长时，运行点在该节点SVCR中变化轨迹如图7所示。

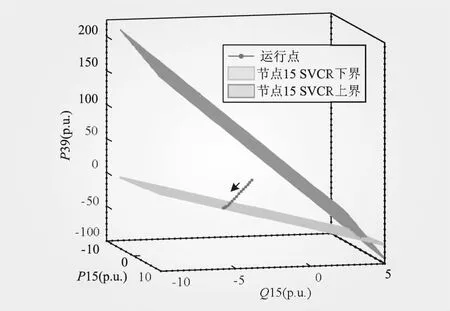
图7 节点15风电增长时的运行点变化轨迹

当风电出力增加1 290 MW时，节点15电压下限安全裕度降低至0.000 946(<10-3，接近于0)，表明节点15电压濒临安全下限。对该极限状态用PSASP软件进行潮流仿真计算，可得节点15电压值为0.938 85，与电压下限相对误差为0.12%，在允许误差范围内。进一步证明了电压安全裕度指标的有效性。

4.2.3 含风电场场景的综合计算

采用所提综合方法对风电出力增加600 MW的状态进行计算，综合指标较大的部分节点结果如表3所示。

表3 含风电场场景综合识别结果(部分)

观察表3中节点15各项指标：电压安全裕度很大，节点电压安全性强，若仅考虑系统因素，其并未被识别为电压薄弱节点；但是，节点15无功-电压灵敏度数值最大，受风电功率变化影响最大；综合来看，节点15综合指标大小已位于评估节点前五位，被识别为系统中的电压薄弱节点。进而，由式(19)可知，若节点电压安全性弱，电压安全裕度较小，综合指标会急剧增大，如表中节点25；若节点自身安全性较强，但受风电功率变化影响较大，其电压安全面临风电随机性、波动性的威胁，无功-电压灵敏度较高，综合指标也会相应增大，如节点15。以上分析表明，综合指标兼顾了节点自身安全性和受风电影响程度两个方面，对电压薄弱节点识别的结果比单一指标更加全面。

4.3 多风电场场景下仿真计算

为模拟多风电场接入系统的场景，基于节点15风电场出力1 290 MW场景，将节点8也接入风电场(功率因数设定为0.95滞后)，令其发电量逐渐增加，同步减少节点15风电场出力，保持整个系统风电总出力不变。节点8、15电压安全裕度如图8所示。

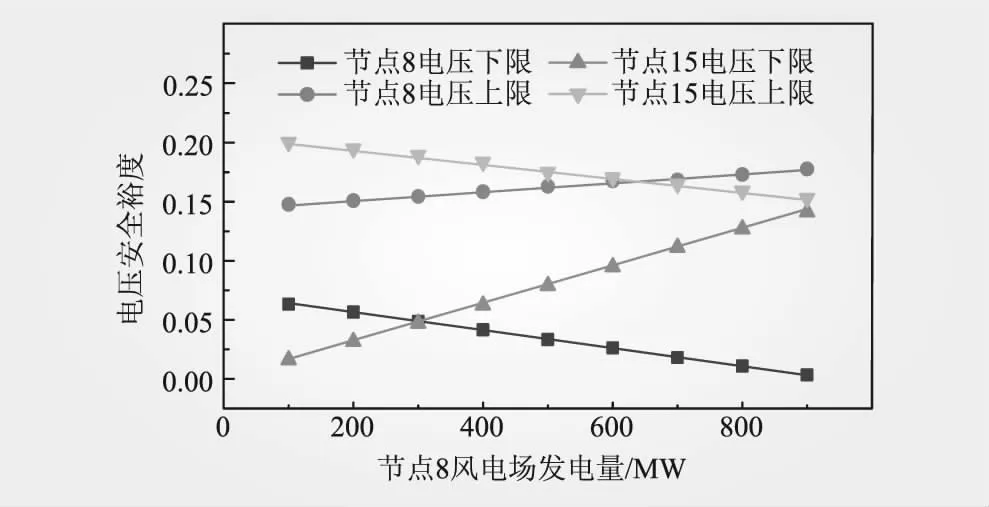
图8 节点8、15电压安全裕度变化情况

由图8可以看出，当节点8风电场发电量为300 MW(节点15风电场发电量为990 MW)时，节点8、15电压下限安全裕度接近，表明节点15接纳风电能力更强。利用电压安全裕度指标进行判别，可为系统中风电接入点及接入量的确定提供帮助，减轻后期电压调控及无功补偿的压力。

根据2.2节方法，确定节点8、15两个风电场无功-电压灵敏度的权重系数分别为0.693 865、0.306 135，灵敏度结果如图9所示。

由图9可以看出，节点8风电场无功-电压灵敏度中，节点8数值最大，其次是节点7、5、6，而节点20、29极小；节点15风电场无功-电压灵敏度中，节点15数值最大，其次是节点16、24、14，而节点1、29极小。结合系统拓扑及参数可知，节点无功-电压灵敏度数值和与风电场接入点间的电气距离呈负相关。赋权后的总灵敏度兼顾了两个风电场的影响。

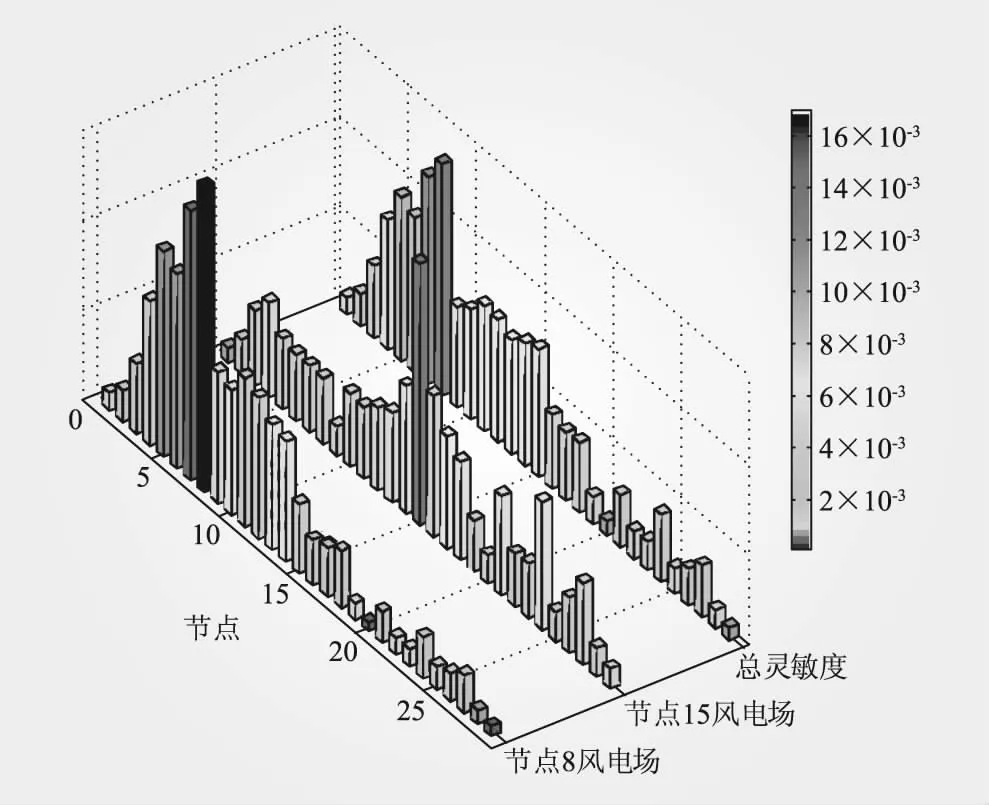
图9 多风电场场景无功-电压灵敏度

对多风电场场景进行综合识别计算，部分典型节点结果如表4所示。

表4 多风电场场景综合识别结果(部分)

由表4可以看出，节点8电压安全裕度极小，电压安全性极弱，同时，其总灵敏度最大，受风电功率变化影响最大，综合指标极大，被识别为电压最薄弱的节点；节点7电压安全裕度非极小，但其总灵敏度很大，受风电影响大，综合指标位于第2位，仍被识别为薄弱节点；节点25灵敏度较小，受风电影响小，但其电压安全裕度较小，节点自身安全性弱，综合指标位于第3位，也被识别为薄弱节点。以上分析表明，本文方法能兼顾系统及风电场两个方面的因素，将自身安全性弱或对风电敏感的节点识别为电压薄弱节点。

5 结 论

本文提出了适用于大规模风电接入系统的电压越限薄弱节点综合识别指标及方法，并通过算例进行验证，相关结论如下：

(1)大规模风电接入系统功率注入不确定性显著，在众多指标中，电压安全裕度考虑了系统电压安全水平运行要求，能反映系统实际可接受的功率波动量，更符合运行人员的需求。

(2)本文在分析大规模风电接入系统节点电压安全性时，考虑到功率转移方向的不确定性，改进了以往连续潮流法求取PV曲线过程中设定的特定功率转移方式，采用基于SVCR的电压安全裕度，涵盖了决策变量的各种转移情况，得到的结果更加全面。

(3)以往的多数指标只从系统方面来考虑，难以敏锐预警风电功率波动带来的安全隐患。本文提出的综合识别指标及方法，能够综合考虑系统和风电场的影响，使电压薄弱节点识别更加合理、全面。

总的说来，本文所提综合识别指标更加全面，综合识别方法快速合理，可以迅速寻找系统电压薄弱节点，研究相应控制措施，对提高系统电压安全水平意义重大。