基于边值法和有限单元法的隧洞衬砌结构计算

马子昌，张继勋，任旭华，张玉贤，王长生，陆嘉伟

(1.河海大学水利水电学院，江苏 南京 210024；2.河南省水利厅西霞院水利枢纽输水及灌区工程建设管理局，河南 郑州 450003；3.上海市政工程设计研究总院(集团)有限公司，上海 200092)

0 引 言

隧洞在引调水工程中发挥着不可替代的作用，其衬砌的计算方法不同，得到的结果会存在差异。水工隧洞设计规范[1]中的边值法衬砌结构计算理论具有丰富的工程经验，其基于结构力学，计算前需假设弹性抗力的分布形式，通过多次迭代计算得到结构位移和内力[2]。

围岩稳定是隧洞安全的关键[3]，有限单元法计算时无需假设荷载分布，与边值法计算时将衬砌结构视为承载主体[4]且计算结果较为保守不同[5]，有限元计算可以考虑衬砌与围岩共同承载[6]，不必假设弹性抗力的分布[7]，其计算结果也更接近真实情况[8]。

本文依托某穿越IV类围岩的引水隧洞，采用Matlab编写边值法程序，计算衬砌结构的内力和位移，之后建立围岩与衬砌的三维流固耦合有限元模型，采用Abaqus计算衬砌结构的内力和位移。通过分析2种方法的计算结果，得到可供类似工程参考的有价值的结论。

1 衬砌计算的边值法

1.1 计算原理

边值法源于结构力学求解方法，计算前，围岩弹性抗力的分布需要假设[9]。边值法将衬砌结构位移和内力计算转化为常微分方程组的边值问题，计算时代入边值条件并多次迭代，使结果不断接近真实解。

将水平荷载qx和垂直荷载qy转化为作用在弧面上的法向荷载qn和切向荷载qτ；取微段ds，根据平衡条件，建立结构内力——轴力T、剪力Q和弯矩M与法向力qnds和切向力qtds之间的平衡方程。微段上的荷载和内力见图1。

图1 衬砌微段上的荷载和内力

根据结构内力与位移关系和边值条件，将衬砌内力和位移计算转化为常微分方程组的边值问题。采用逐次近似法，首次计算时假设各微段的弹性抗力为0，求出衬砌结构的内力和位移；后续计算的抗力分布采用前1次的计算结果；迭代计算至相邻2次计算得到的抗力分布相同时，计算结束。

1.2 计算荷载

隧洞的运行工况、检修工况、施工完建工况所需计算的荷载包括衬砌结构自重、围岩压力qk、注浆压力、内水压力和外水压力。

衬砌容重取25 kN/m3，围岩压力qk采用坍落拱理论计算，水平方向围岩压力qkh为17.168 kN/m，垂直方向围岩压力qkv为58.013 kN/m。在顶拱120°范围内施加200 kN/m的灌浆压力。在运行期，内水压力为660 kN/m。在运行期和检修期，由于内水外渗，外水压力取内水压力的0.6，为396 kN/m；在施工期，外水压力根据区域的地下水位确定，为151 kN/m。

2 衬砌结构计算

2.1 边值法

某引水隧洞Ⅳ类围岩结构断面见图2。衬砌顶拱中点处位置记为0，顶拱水平位置为6.123 m，弧线与直线段连接处位置为7.075 m，侧墙与底板连接处位置为10.125 m，底板中点位置为13.175 m。在边值法计算时，采用Matlab编写四阶龙格-库塔法的边值法求解程序，选择顶拱中点和底板中点作为对称点，以对称点处的切向位移、转角和剪应力为0作为边值条件，计算衬砌结构的内力和位移。

图2 引水隧洞Ⅳ类围岩结构断面(单位：mm)

程序计算时，需输入衬砌的长度、微段的数目以及衬砌的厚度、材料的弹性模量、剪切模量，输入作用在衬砌上的荷载，输入围岩抗力系数、初始的弹性抗力分布以及边界条件。3种工况下，衬砌的弯矩、轴力和法向位移值见图3～5。衬砌的顶拱和底板中点的弯矩、轴力和法向位移的计算结果见表1。分析可知：

表1 顶拱和底板中点的内力和位移

图3 运行工况计算结果

图4 检修工况计算结果

图5 施工完建工况计算结果

(1)在运行工况和检修工况，弯矩、轴力和法向位移变化趋势相似，衬砌弯矩的最大值均出现在顶拱中点处，但方向相反，弯矩值在顶拱段不断减小，在侧墙和底板段达到最小。轴力在顶拱与侧墙连接处达到最小，在顶拱和底板处轴力大小相近，方向相反。2种工况下，衬砌的法向位移方向相反，由顶拱中点向侧墙段先少量增加后急剧减小，至侧墙连接处降至最小，侧墙与底板的法向位移值相近。

(2)在施工完建工况，弯矩值由顶拱向侧墙不断增加，在底板处，弯矩值不断减小。轴力在顶拱段先减小至0后反向增加，经过水平位置后，轴力不断减小。法向位移由顶拱向侧墙不断减小，在底板处达到最小。

结果表明，截面弯矩在顶拱与侧墙交点附近易产生拐点。存在内水压力时，衬砌结构为外侧受拉，在顶拱会产生拉力，衬砌结构的法向位移方向指向衬砌外法线方向；不存在内水压力时，衬砌结构表现为外侧受压，所产生的轴力均表现为压力，衬砌结构法向位移方向为结构内法线方向。

2.2 有限元法

在ABAQUS中，模型计算范围取为隧洞直径的5倍。模型大小：顺水流向取1 m、垂直水流向取39 m、高度方向取39 m。模型左右侧、前后面均取法向约束，底面取法向和切向约束。假定围岩和衬砌结构为各向同性、均匀连续的弹性体。衬砌结构和围岩均采用C3D8P单元，采用弹性本构。有限元模型见图6。

图6 引水隧洞围岩衬砌结构网格划分

运行工况计算步骤如下：①设置地应力和孔隙水压力初始条件，进行地应力平衡；②采用稳态渗流分析步，将衬砌内侧孔隙水压力设置为内水压力值，计算衬砌结构的应力和位移[10]。检修工况的计算，在运行工况计算的基础上，增加1个瞬态分析步，将衬砌内侧孔隙水压力设置为0，计算衬砌结构的应力和位移。施工完建工况采用应力释放法进行模拟，计算步骤如下：①取消激活衬砌单元，在围岩的开挖边界处增加x、y、z向的约束，设置地应力和孔隙水压力初始条件，进行应力平衡；②提取开挖边界处约束力，移除开挖边界处的约束，将约束力以集中力的形式其施加到开挖边界的结点上；③将开挖边界上的集中力释放0.1；④激活衬砌单元，并将开挖边界上的集中力完全释放。

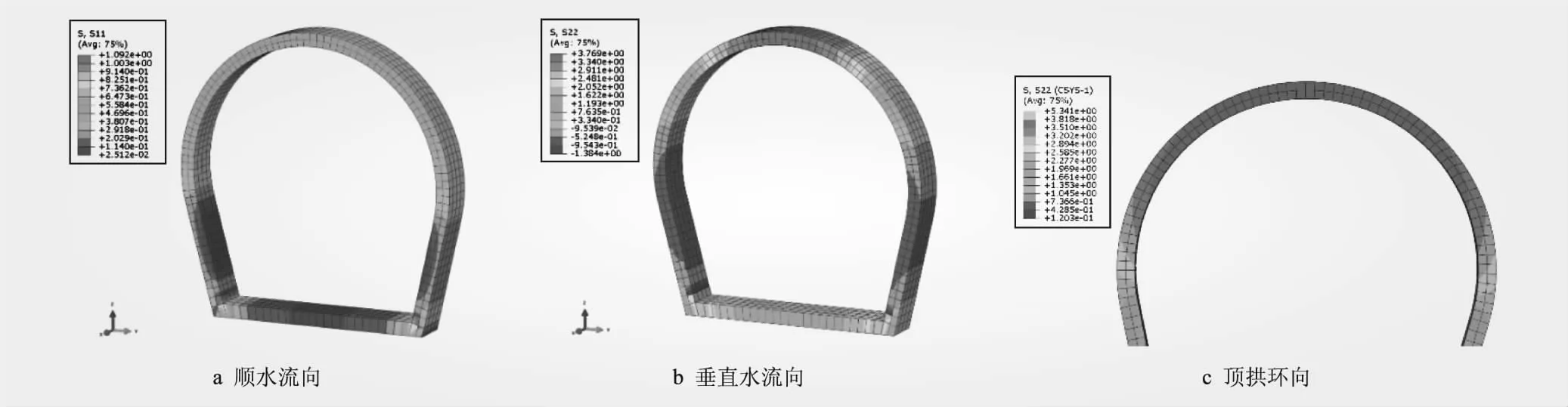
图7 运行工况应力

图8 检修工况应力

2.2.1 位移

衬砌结构各工况下的位移见表2。从表2可知，运行工况下，衬砌结构的位移值在0.404～1.892 mm之间，最大位移值出现在底板中部，衬砌结构的位移较小。检修工况下，衬砌结构的位移值在1.009～1.363 mm之间，最大位移值出现在侧墙顶拱交接处，衬砌结构的位移较小。施工完建工况下，衬砌结构的位移值在0.954～1.255 mm之间，最大位移值均出现在侧墙顶拱交接处，衬砌结构的位移较小。

表2 衬砌结构各工况位移 mm

2.2.2 应力

衬砌结构各工况下的应力云图见图7～9。应力峰值见表3。分析可知：

表3 各计算工况下的应力 MPa

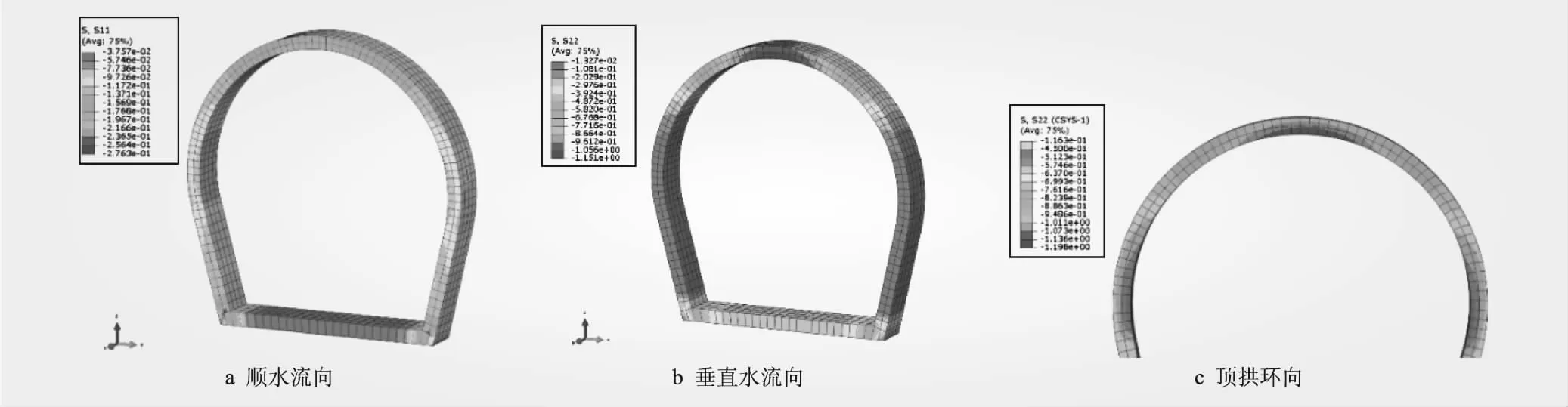
图9 施工完建工况应力

(1)在运行工况，衬砌各部位均出现了顺水流向拉应力，最大值为1.092 MPa，位于侧墙与底板连接处。垂直水流向的最大拉应力为3.769 MPa，位于顶拱中心。顶拱各部位均出现了环向拉应力，最大值为3.818 MPa，位于顶拱中心。

(2)在检修工况，衬砌各部位未出现顺水流方向的拉应力。顶拱、底部和侧墙均出现了垂直水流向拉应力，最大值为0.003 MPa，位于侧墙底部内侧。顶拱各部位均未出现环向拉应力。

(3)在施工完建工况，衬砌各部位均未出现顺水流向、垂直水流向以及环向拉应力。

2.3 衬砌环向配筋

采用边值法计算结果进行配筋时，需根据截面的弯矩M和轴力T，选择危险截面。对于顶拱，由于截面的弯矩和轴力在顶拱中点处的数值较大，选择中点所在截面作为最危险截面，在运行工况下，按照偏心受拉构件配筋，在检修和施工完建工况下，按照偏心受压构件配筋。在侧墙与底板部分，由于弯矩和轴力产生的截面拉应力小于混凝土抗拉强度，只需按照构造要求配筋。

采用有限元计算结果配筋时，按照应力图形面积对衬砌结构配筋计算。根据截面的拉应力图形，计算出拉应力合力，由钢筋承担截面拉力并计算钢筋面积。

隧洞衬砌配筋控制工况为运行工况，控制截面分别为顶拱中点和底板中点，各截面在1 m范围内的配筋计算结果见表4。从表4可知，采用有限单元法计算得到的配筋面积小于边值法。

表4 衬砌结构应力配筋结果 mm2

3 结 语

本文采用边值法和有限单元法，对某引水隧洞在运行、检修和施工完建工况下衬砌结构进行受力分析，得到以下结论：

(1)边值法和有限单元法计算得到的衬砌结构内力和位移的变化规律相同。在运行工况，衬砌结构外侧受拉，顶拱出现拉应力，衬砌结构有向外扩张的趋势；在检修工况和施工完建工况下，衬砌结构表现为外侧受压，衬砌结构有向内压缩的趋势。

(2)采用边值法和有限元法计算衬砌结构的内力，其最大值出现的部位相同。在运行工况和检修工况，内力最大值均出现在顶拱中点处，在底板段弯矩值达到最小；施工完建工况的内力最大值均位于侧墙处，在底板和顶拱的内力值较小。有限元计算考虑了衬砌与围岩联合承载，计算结果普遍小于边值法。

(3)由于有限元法能够考虑围岩与衬砌联合承载，在相同的截面尺寸下，采用有限元计算结果的配筋面积更小。