基于重要度排序的配电自动化终端优化布局方法

李 锰，张庆庆，许长清，何 婧，李 成

(1. 国网河南省电力公司经济技术研究院，河南 郑州 450052；2. 湖南大学，湖南 长沙 410082)

近年来，用户对供电可靠性的要求越来越高，如何提升供电可靠性成为电网公司迫切需要解决的问题。在配电馈线上装设配电自动化终端是提高供电可靠性的重要手段。配电自动化终端主要分为“三遥”终端和“二遥”终端两类。“三遥”终端可以同时实现遥测、遥信、遥控功能，对供电可靠性提升作用大，单价高；“二遥”终端只具备遥测和遥信功能，对供电可靠性提升效果相对较小，单价低。给所有开关装设三遥终端能在很大程度上提升供电可靠性，降低用户停电损失，但所需投资费用太高，导致总体经济性较低。配电自动化终端优化布局就是综合考虑设备投资及停电损失两部分费用的平衡，在满足供电可靠性等技术指标要求的前提下，确定使综合费用最低的“三遥”“二遥”终端安装数量及安装位置。

针对配电自动化终端优化布局问题，目前国内外学者已经进行了一系列研究。国家电网公司出台的《配电自动化规划设计技术导则》(Q/GDW11184-2014)中规定，应根据可靠性需求、网架结构和设备状况，合理选用配电终端类型。对于关键性节点，如主干线联络开关、必要的分段开关，进出线较多的开关站、环网单元和配电室，宜配置“三遥”终端；对于一般性节点，如分支开关、无联络的末端站室，宜配置“二遥”终端[1]。在运用上述导则进行终端布局时，关键性节点及一般性节点的界定存在主观性，工作人员只能根据工作经验得出大致的布局方案。文献[2]在假设用户均匀的条件下，从供电可靠性及投入产出比的角度分析每条馈线需要配置的“三遥”“二遥”终端数量，对于大规模配电网的终端数量规划具有指导意义。文献[3]建立了以等年值总费用最小为目标函数，供电可靠性要求为约束条件的配电自动化终端布局模型，并采用遗传算法求解该模型。所提方法能够解决小规模具体配电网络中终端配置规划问题，但是对于大规模配电网，遗传算法的求解效率及稳定性可能无法满足要求。文献[4]提出了一种新的配电自动化终端可靠性分析方法，并以此为基础构建了“三遥”终端布局模型，运用商业软件LocalSolver求解该模型。文献只针对“三遥”终端的布局进行了讨论，针对“二遥”终端的布局没有说明。文献[5]提出了一种配电自动化终端分阶段选型选址办法。文中在假设馈线中的分段开关都会安装终端的前提下，首先确定使目标函数最低的“二遥”“三遥”终端数量，然后根据各节点的重要度排序依次选择各节点安装终端类型。所提方法能够有效提高求解效率，但是文中终端选型时没有考虑节点不安装终端的情况，而且终端选址时没有考虑优先布置的终端对后续终端重要度排序的影响。

针对上述问题，本文提出了一种基于重要度排序的终端优化布局算法。构建了以等年值综合费用最低为目标函数，供电可靠性和投入产出比为双重约束的终端布局优化模型；用供电可靠性的提升来度量节点终端的重要度，并考虑了布局优化过程中节点关联性对重要度的影响，提高了规划寻优效率。仿真结论表明相对于智能优化算法该模型求解质量和求解速率都有显著提高。

1 配电自动化终端布局优化模型

1.1 目标函数

配电自动化终端布局模型的目标函数为：

obj.min (CE+CM+CI)

(1)

式中：CE为设备投资等年值费用，CM为设备年运行维护费用，CI为用户年停电损失费用。设备投资等年值费用CE的计算公式如式(2)所示。

(2)

式中：M为设备种类数量(设备类型包括“三遥”终端、“二遥”终端、相应的通信设备)；Nk表示第k种终端设备的安装数量；Czk表示第k种终端设备的单价；i为贴现率；nk为第k种设备的使用年限。

设备年运行维护费用CM一般以设备投资年等值费用的百分比给出，如式(3)所示，α为比例系数。

CM=αCE

(3)

年停电损失费用是指设备故障、停电检修等对用户造成的停电损失。停电损失与停电持续时间、负荷类型、负荷大小等因素有关。常见的停电损失计算方法有平均电价折算倍数法、产电比法和总拥有费用法[6]。本文综合产电比法及平均电价折算倍数法来计算用户停电损失，计算公式为[7]

CI=(λ1K1+λ2K2)WENS

(4)

式中：λ1和λ2分别为产电比法和平均电价折算倍数法的权重；K1为产电比；K2为单位停电电量电价；WENS为配电网年缺供电量期望值。

1.2 约束条件

本文构建的配电自动化终端布局模型考虑了供电可靠率及投入产出比两个约束条件，供电可靠率约束如(5)所示。

ASAI≥ASAIset

(5)

式中：ASAI为终端布局后规划区域的供电可靠率，ASAIset为规划区域的供电可靠率要求值。

投入产出比是项目评价的一项重要经济效益指标，投入产出比约束如(6)所示。

γ≥γset

(6)

式中：γ为终端布局方案的投入产出比，γset为规划文件要求的投入产出比，γ的计算方式为

(7)

式中：M、Nk、Czk的含义与式(1)相同；Ny为评价年限；CLb为终端布局前的年停电损失费用；CLa为终端布局后的年停电损失费用。

2 节点终端安装重要度定义及计算公式

2.1 含配电自动化终端的配电网故障处理过程

以图1所示10kV馈线为例，对含配电自动化终端的配电网故障处理过程进行介绍。当馈线段L3发生故障时，配电网故障处理步骤如下：

(1)变电站出线断路器跳闸并重合闸失败，主站接收到各个配电自动化终端上传的遥测、遥信信息后根据故障定位算法[8-11]，将故障定位在S2和S4之间，该区域为自动故障定位区间。

(2)自动故障定位完成后，主站向离自动故障定位区间最近的三遥开关(安装了三遥终端称为三遥开关)S1和S4下达分闸命令，三遥开关S1与S4之间的区域为自动故障隔离区间。

(3)故障自动隔离后，出线断路器及联络开关迅速合闸，负荷点LP1、LP5分别通过主电源及联络线恢复供电。LP1和LP5的停电时间为主站自动故障定位时间与开关自动分合闸时间之和，记为t1。

(4)工作人员赶到故障现场，在自动故障定位区间内查找故障元件。找到故障元件后，手动断开S2和S3并合上S1及S4，负荷点LP2、LP4恢复供电。LP2与LP4的停电时间为故障查找时间t2与开关手动分合闸时间t3之和。

(5)此后，对L3上的故障元件进行修复，修复完成后，合上S2及S3，负荷点LP3恢复供电。LP3的停电时间为故障查找时间t2、开关手动分合闸时间t3及故障修复时间t4之和。

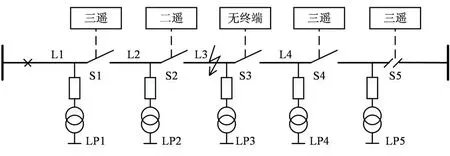
图1 配电网馈线示意图

2.2 节点三遥终端安装重要度定义及计算公式

在前文所述故障处理过程中的故障隔离阶段，由于在S1和S4处安装了“三遥”终端，主站能够对开关直接进行遥控操作，使负荷点LP1及LP5的停电时间减小，停电损失降低。然而在不同位置处安装三遥终端对用户停电损失的影响是不同的。例如在图1中，若只将S1配置为“三遥”终端，当L1发生故障时，相较于不配置终端的情况，LP2、LP3、LP4的停电时间都会由故障查找时间与人工故障隔离时间之和t2+t3缩短为主站自动故障定位时间与开关自动分合闸时间t1；若只将S2配置为“三遥”终端，则只有LP3、LP4的停电时间由t2+t3缩短为t1;若只将S3配置为“三遥”终端，则只有LP4的停电时间由t2+t3缩短为t1。同理可以分析分别在L2、L3、L4馈线段故障时，在各位置配置“三遥”终端对各负荷停电时间的影响，由此可以构造负荷影响矩阵，如式(8)所示。

(8)

矩阵元素T1(ij)表示在j位置配置“三遥”终端后，Li发生故障时，停电时间由t2+t3缩短为t1的负荷点集合。

在某处安装“三遥”终端后，停电时间由t2+t3缩短为t1的负荷量越大，表明在该位置安装“三遥”终端对可靠性提升的作用更大。本文将某位置“三遥”重要度定义为，在该位置配置“三遥”终端后，不同馈线段发生故障时，停电时间由t2+t3缩短为t1的负荷量的加权和。第j个待选位置的“三遥”影响度D3(j)的计算公式如(9)所示。

(9)

式中：nL表示馈线段数量，对于图1所示馈线，nL为5；pi表示第i段线路发生故障的概率；T1(ij)是负荷影响矩阵中的元素；Pk表示第k个负荷点的平均功率。

2.3 节点二遥终端安装重要度定义及计算公式

在前文所述故障处理过程中的故障定位阶段，由于安装“二遥”及“三遥”后，主站能够根据终端上传的遥测及遥信信息进行故障定位，使工作人员查找故障的范围由整条馈线缩短为L3+L4，若工作人员对整条馈线进行故障排查的时间为ts，则缩短的故障查找时间为

(10)

然而在不同位置安装二遥终端，缩短的故障定位范围是不同的。例如在图1中，若只将S1配置为“二遥”终端，当L1发生故障时，相较于不配置终端的情况，缩短的故障定位范围为L2+L3+L4；若只将S2配置为“二遥”终端，缩短的故障定位范围为L3+L4；若只将S3配置为“二遥”终端，缩短的故障定位范围为L4。同理可以分析分别在L2、L3、L4发生故障时，在不同位置处配置“二遥”终端而缩短的故障定位范围。由此可以构建定位范围缩小矩阵，如式(11)所示。

(11)

矩阵元素T2(ij)表示当Li发生故障时，由于在j位置配置“二遥”终端而缩短的故障定位范围。

人工故障定位范围缩小后，对于所有停电时间包含人工故障查找时间的负荷点而言，停电时间都得到减小。在某位置安装“二遥”终端后，减小的停电量越大，表示在该位置安装“二遥”终端对可靠性提升的作用更大。本文将“二遥”重要度定义为，在该位置配置“二遥”终端以后，在不同馈线段发生故障时，停电时间减小的负荷量的加权和。第j个待选位置的“二遥”安装重要度D2(j)的计算公式如式(12)所示。

(12)

式中：nL和pi的定义与式(9)相同；T2(ij)是定位区域影响矩阵中的元素；Lk表示第k段馈线的长度；Ltotal为该馈线的总长度；Plocate为停电时间包含人工故障查找时间的负荷总量，即自动故障隔离区与人工故障隔离区之间的负荷总量，只取决于“三遥”终端的安装情况，对于“三遥”终端已经配置好的馈线，Plocate是确定的。

3 基于重要度排序的配电自动化终端布局

3.1 安装数量确定时三遥终端选址方法

由矩阵T1及式(9)可以计算出每个待选位置的“三遥”重要度，从小到大进行排序，重要度最大的待选位置作为第一个“三遥”终端安装点。若“三遥”终端的安装数量不止一个，则首先需要对负荷影响矩阵中的元素进行剔除，再计算各个待选位置节点的三遥终端安装重要度，选择重要度最大的位置作为“三遥”终端的安装点。依此类推，直到所有“三遥”终端选址完成。安装数量确定时“三遥”终端选址流程如图2所示。

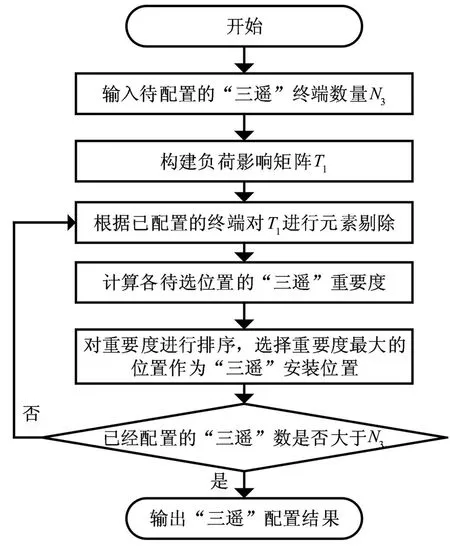
图2 安装数量确定时“三遥”终端选址流程

在上述过程中，对负荷影响矩阵中的元素进行剔除的思路为若第k个开关已经安装了“三遥”终端，则将Tik包含的负荷点从Tij中删除，因为这些负荷点馈线发生故障时，已经能被三遥开关k自动隔离，在其他位置安装“三遥”终端并不会减小这些负荷点的停电时间。例如在图2所示馈线中，假设待安装的“三遥”终端数量为2个，若S3为第一个“三遥”终端的安装点，在确定第二个“三遥”终端安装点时，首先需要对式(11)所示矩阵进行修改，将Ti3包含的元素从Tij中删除，修改后的矩阵如(13)所示。此后根据式(13)重新计算各位置三遥终端安装重要度，选择重要度最大的位置作为第二个三遥终端安装点。

(13)

3.2 安装数量确定时二遥终端选址方法

安装数量确定时二遥终端选址思路与三遥终端的选址思路类似。首先根据矩阵T2及公式(12)计算出每个待选位置的“二遥”重要度，从小到大进行排序，重要度最大的待选位置作为第一个“二遥”终端安装点。上一个“二遥”终端选址完成后，修改定位范围缩小矩阵重新计算各节点的二遥终端安装重要度，重要度最大的位置作为下一个“二遥”终端的安装点。修改定位范围缩小矩阵的思路为若第k个开关已经安装了“二遥”或者“三遥”终端，则将Tik包含的元素从Tij中删除。

3.3 三遥及二遥终端整体布局流程

3.1和3.2节对给定安装数量下“三遥”及“二遥”终端选址问题进行了阐述，但是最优的终端安装数量尚未明确。本文采用枚举法，对所有可能的“二遥”“三遥”终端数量组合情况进行位置优化，计算每种布局结果的目标函数及约束条件，从中选出满足约束条件且目标函数最小的布局结果作为最优方案。具体的终端布局流程如图3所示。

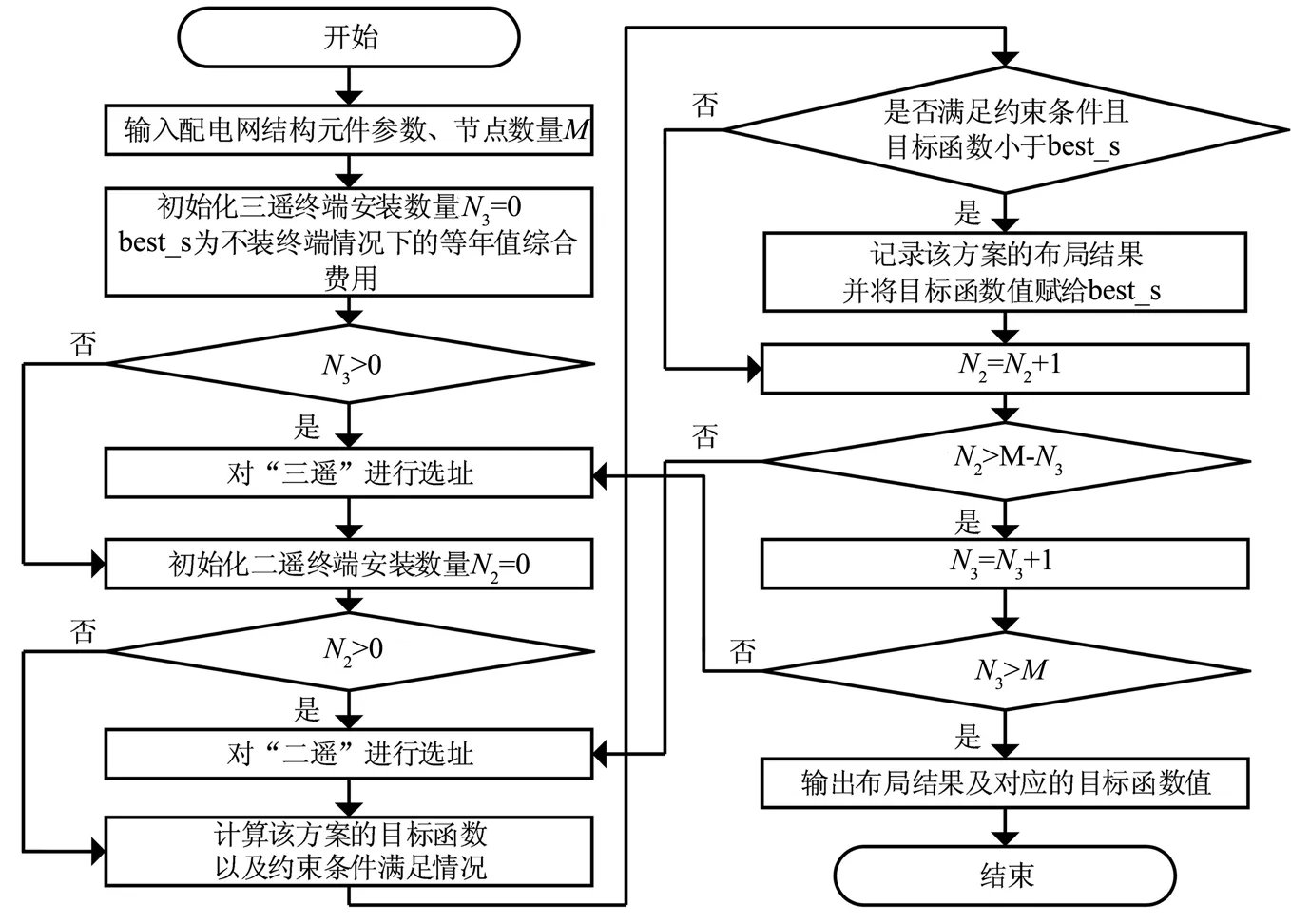
图3 终端布局流程图

4 实例分析

选应用所提方法对IEEE RBTS BUS2 算例进行终端优化布局。该系统共有22个负荷点，1908户用户，总平均负荷为12.291MW，计算中假设系统各点负荷为原负荷的2倍,算例接线图如图4所示。本文假设用户分支馈线上都已安装熔断器、出线断路器和联络开关均安装了“三遥”终端，主要针对10个分段开关进行终端配置。算例的电气参数和可靠性参数见文献[12]。计算中，“三遥”终端及其配套的通信设备单价为5.4万元/组，“二遥”终端及其配套的通信设备单价为1.05万元/组。设备的使用寿命为10年；年运行维护费用占投资费用的3%；产电比法和平均电价折算倍数法的加权系数分别取0.36和0.64；产电比K设为6.652元/kW·h；单位停电电量电价设为11.25元/kW·h[12]。故障处理过程中的时间参数如表1所示。本文假设系统中所有变压器发生故障时都直接进行更换处理，在不配置任何终端时该系统供电可靠率指标为99.988%，供电可靠率指标约束值ASAIset设为A类地区供电可靠率要求值99.99%[1]。

表1 时间参数

在不设置投入产出比约束的情况下，分别运用本文方法及遗传算法对该系统进行终端优化布局，遗传算法的参数设置为：种群规模50，最大迭代次数200，交叉率0.8，变异率0.2。终端布局结果及经济指标如表2所示，表2中遗传算法的布局结果取20次计算中的最优解，计算时间为20次计算的平均时间。

由表2可知：采用本文方法求得的终端布局结果与遗传算法20次计算中最优解的结果相同，但本文算法的计算时间只需要0.0529 s，遗传算法的计算时间为4.3 s，遗传算法的计算时间约为本文算法计算时间的81倍。

表2 RBTS-BUS2终端布局优化结果

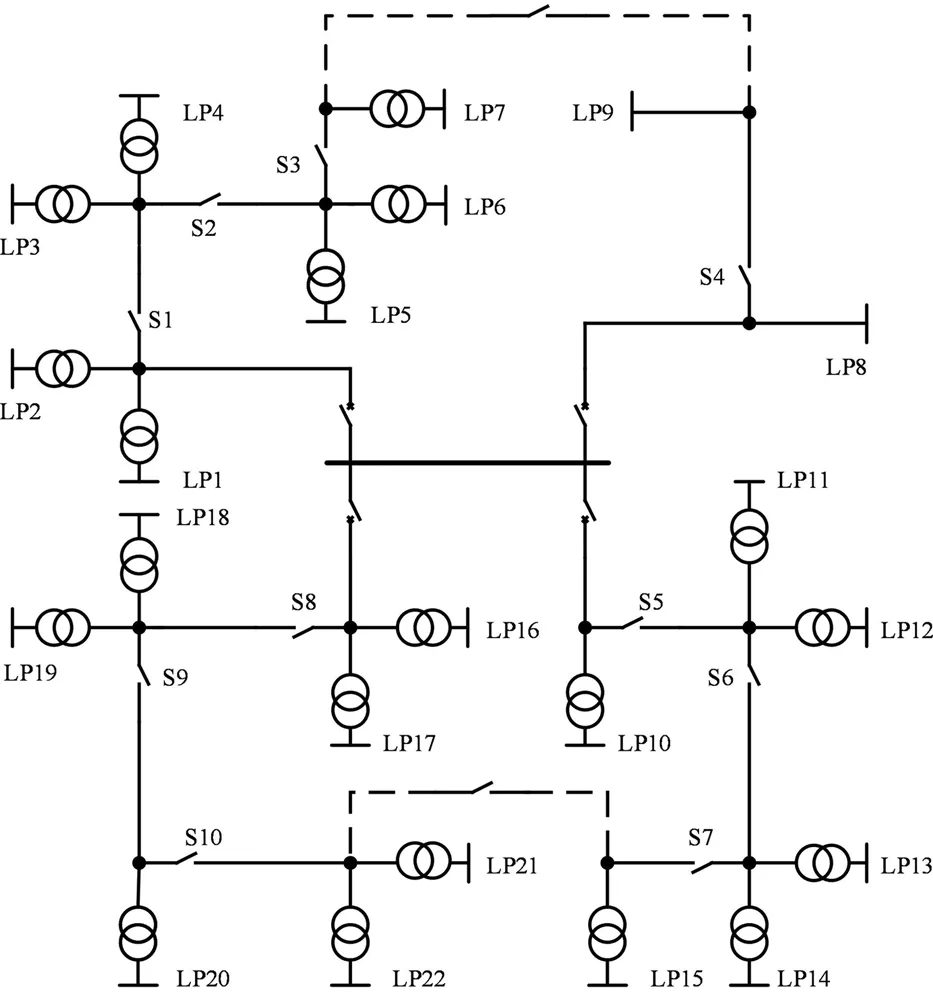
图4 IEEE RBTS BUS2算例接线图

表2中最优方案的投入产出比为2.12，当投入产出比约束大于该值时，运用本文方法对不同投入产出比约束的情形进行终端布局，不同约束条件下布局结果费用随投入产出比变化的关系如图5所示。

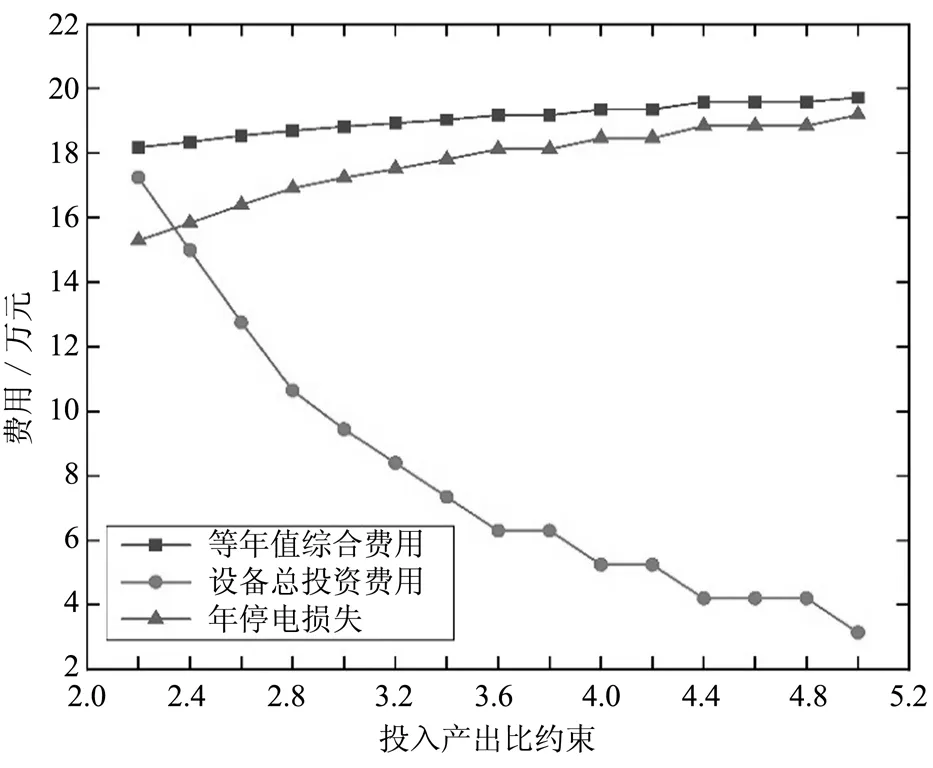
图5 不同投入产出比约束下各项费用变化趋势

由图5可知随着投入产出比约束值的增加，最优终端布局结果的等年值综合费用及年停电损失费用逐渐增加，增加幅度较小；设备初始投资费用逐渐减小，减小幅度较大。

“三遥”及“二遥”终端单价差异的大小会对终端安装数量产生影响。假设“二遥”终端单价仍为1.05万元/组，“三遥”终端的单价是“二遥”终端单价的n倍。不同n情形下，“三遥”及“二遥”终端安装数量如图6所示。

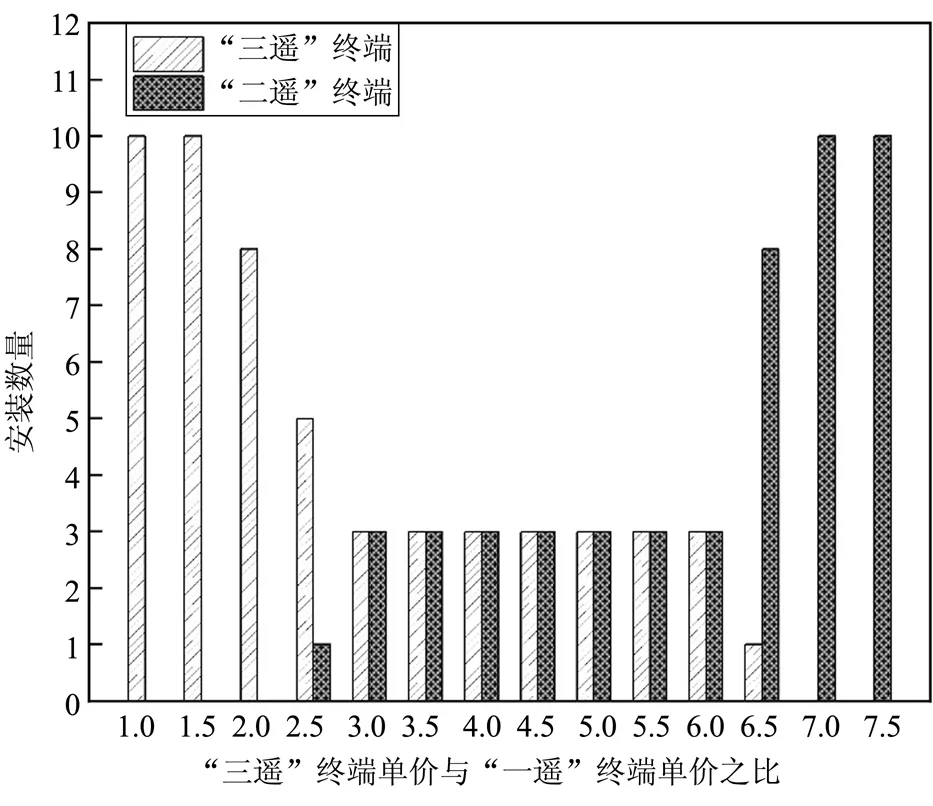
图6 终端安装数量与终端单价比之间的关系

由图6可知：当“三遥”终端与“二遥”终端单价比小于1.5时，由于两种类型终端的价格差异较小，“三遥”终端对供电可靠性提升作用更大，馈线上应全部安装“三遥”终端；当“三遥”终端与“二遥”终端单价比大于2且小于3时，随着单价比增加，“三遥”终端安装数量逐渐减小，“二遥”终端安装数量逐渐增多；当“三遥”终端与“二遥”终端单价比位于[3,6]之间时，“三遥”及“二遥”终端的安装数量均保持不变；当单价比大于6.5且小于7时，随着单价比增加，“三遥”终端安装数量减小，“二遥”终端安装数量增多；若单价比大于7，由于“三遥”终端价格过高，为了使等年值综合费用最低且保证供电可靠性提升要求，馈线上应全部安装“二遥”终端。在实际规划过程中，工程人员应考虑“三遥”及“二遥”终端单价差异，合理确定“三遥”及“二遥”终端的安装数量。

为了验证本文方法在较大规模配电网中的适用性，在原IEEE RBTS BUS2系统基础上增加10条馈线，负荷点数量由22增加为86，总平均负荷由12.291 MW增加为40.9964 MW，可配置终端的位置数由10增加为44。针对扩充模型，分别运用本文算法和遗传算法进行求解，其中遗传算法的基本参数为：种群规模500，最大迭代次数500，其他参数同上。随机抽取6组遗传算法的结果与本文算法的结果进行对比，如表3所示。

表3 扩充模型终端布局优化结果

采用遗传算法求解终端布局得到的六组随机解中，有两组解与本文算法的求解结果相同，其余四组解均劣于采用本文算法的求解结果，六组解的计算时间均为本文算法的六十倍以上，其余指标的均值也不如本文算法。可见本文算法在保证求解质量的同时，求解效率得到了显著提升。

5 结 论

针对配电自动化终端优化布局问题，提出了一种基于重要度排序的终端优化布局方法。通过分析“三遥”及“二遥”终端安装在不同位置对供电可靠性提升的影响，定义了各节点“三遥”及“二遥”终端安装重要度及计算公式，将安装位置节点“三遥”及“二遥”重要度排序作为终端选址的依据。该方法在对终端进行选址过程中，考虑了已经配置的终端对剩余安装位置重要度的影响，相较于依据节点重要度排序一次性对所有终端进行选址的方法更具合理性。应用本文方法对RBTS BUS2及扩充模型进行终端优化布局，结果表明：相较于遗传算法，本文的求解质量及求解速率都有显著提升，更适用于求解较大规模配电网的终端优化布局问题。