液态金属磁流体发电通道特性分析
2022-12-27李永国朱秋莹李祥燕
李永国, 朱秋莹, 覃 灿, 李祥燕
(1.上海海洋大学 工程学院, 上海 201306; 2.上海海洋可再生能源工程技术研究中心, 上海 201306)
0 引言
随着我国对可再生能源的开发和利用,波浪能受到了国内外学者的高度关注[1]。 从最初的旋转式发电机到直驱式发电机,再到液态金属磁流体 (Liquid Metal Magnetohydrodynamic,LMMHD)直驱式发电机,新的发电机的研究一步步改进了波浪能发电装置的不足之处。 与传统波浪能发电装置相比,直驱式波浪能发电装置可以直接将波浪能转化为电能,省去了中间转化装置,结构更简单,波浪能转化效率更高。 相比于常规的线圈直驱式发电机,液态金属磁流体发电机是利用导电液体来切割磁感线,当液态金属流经发电通道时, 镶嵌在通道两侧的电极上会产生感应电动势。 液态金属磁流体发电机具有发电功率高、结构简单、成本低等优点。 因此,近年来液态金属磁流体发电机被广泛应用在波浪能发电装置研究中。
国外研究磁流体发电的国家主要有美国、俄罗斯、日本等。 Satake S[2]对带有磁流体(MHD)发电机的自由活塞内燃机进行了研究,并分析计算了液态金属磁流体的动力学特性。Niwa N[3]研究了具有非对称方型截面、对称方型截面、圆形截面的磁流体发电机,发现非对称方型截面的发电机具有最高的输出功率。 Yamada K[4]对液态金属磁流体发电机进行三维数值分析, 阐明了MHD 发电机中电磁场和流体流动的三维结构。Hu L[5]分析了液态金属磁流体发电系统在汞、U-alloy47 和NaK78 等3 种不同工作流体下的发电性能, 分析结果表明, 具有低密度和高导电性能的液态金属可以有效提高发电效率。
我国也非常重视对磁流体发电技术的研究。乔凯[6]将LMMHD 与震荡水翼捕能技术结合,基于Fluent 软件对发电通道的特性进行分析, 分析结果表明:高宽比越小,端部效应的作用越明显;电极过长或过宽都会降低发电效果。易仁义[7]研究了相关参数对液态金属发电机输出特性的影响,研究结果表明,空载电压与入口速度、磁感应强度、发电通道宽度成正比,但是发电通道宽度越大,空载电压的相对误差就越大。程邦勤[8]对磁流体发电通道进行了数值模拟研究,研究结果表明:增大磁感应强度或电导率可以增加能量的提取率。 赵凌志[9]利用建立的等效电路模型计算了LMMHD 发电机试验样机的输出特性。 张宇磊[10]建立三维矩形截面发电通道模型对LMMHD 发电进行数值模拟分析,分析结果表明:改变发电通道的参数会导致电磁效率和端部效应程度等发生明显的变化;若保持通道宽度和相互作用参数不变, 则电磁效率和端部效应程度等也基本保持不变。
国内外学者对液态金属磁流体发电技术进行了许多研究,但是,对于通道参数对液态金属磁流体发电性能影响的研究还不够深入,对于液态金属磁流体发电技术在工程中的应用还缺乏一定的理论数据支撑。 因此,本文通过数值模拟的方式对发电通道参数对液态金属磁流体发电性能的影响进行研究,从而为发电通道参数的选取提供理论基础。
1 液态金属磁流体发电理论
液态金属磁流体发电机是基于法拉第电磁感应原理建立的。 当导电液态金属垂直流经磁场,流体切割磁力线从而产生感应电动势[11]。 在通道的内侧装上正负电极,当接通外接负载时,导电流体产生的能量便可以直接转换成电能输出。
液态金属磁流体发电通常采用具有高电导率、低熔点的液态金属作为发电工质。常见的液体金属有镓铟锡合金、钠钾合金和汞,其主要物理性质如表1 所示[12]。 镓铟锡合金作为导电液态金属时,其发电性能要优于钠钾合金和汞,故本文选取镓铟锡合金作为磁流体发电介质[10]。

表1 液态金属的物理性质Table 1 Physical properties of liquid metal
图1 为液态金属磁流体发电通道的计算模型(通道宽度为d、高度为h、长度为L)。导电液态金属以速度v 沿z 轴负方向流进磁流体发电通道内部,磁场方向与流体方向垂直且与y 轴方向相同。在理想条件下,假设电磁场和流场以均匀分布的形式存在于空间中,不考虑诱导磁场的影响,在两个电极壁面加载负载R 后,可推导出液态金属磁流体的稳态发电性能参数如下所示[13]。

图1 液态金属发电通道模型Fig.1 liquid metal power generation channel model
通道内阻r:


2 磁流体发电通道数值模拟讨论分析
本文利用Fluent 软件下的MHD 模块进行数值模拟计算, 选用镓铟锡合金作为磁流体发电介质[14]。 空载时选用诱导磁场法进行研究。 有负载时,考虑到磁流体发电通道的基本参数不变,只是负载电压有所不同,不会引起诱导磁场的变化,因此选用电势法进行研究。
2.1 边界条件和初始条件设置
在仿真分析时需要设定磁流体发电通道的边界条件和初始条件。 本文设定的两个电极壁面为铜电极导电壁面; 边界条件需满足电流可以流过而液体不可以流过, 因此电极与液态金属的接触面采用耦合壁面。通道入口需要赋予一定的速度,因此设置速度入口,通道出口则设置为压力出口,其余的壁面设置为绝缘壁面。在计算时,电极表面产生的电势值的大小与负载系数的大小有关,正负极的电势值。
2.2 发电通道数值模拟分析
本文的计算模型见图1。 该模型为矩形发电通道,通道截面尺寸为0.04 m×0.24 m,通道长度为0.58 m。 如图1 所示, 电极布设在发电通道中部,材质为铜,长度为0.26 m,宽度为0.04 m。磁场方向沿y 轴,分布区域为电流通过的区域,即与电极作用的区域一致。 发电通道其余壁面均设置为绝缘材质,且采用的液态金属为镓铟锡合金。通过对磁流体发电通道的三维模型进行数值模拟计算, 可研究不同负载系数和不同磁感应强度下发电通道内的流动现象。
当磁感应强度B 为0.5 T,负载系数k 分别为0.17,0.33,0.5,0.67 和0.83 时,发电通道内磁流体的速度变化规律如图2 所示。从图2 可以看出,在5 种负载系数下, 发电通道内磁流体的速度变化规律是相似的,即经过有效发电段时,边界层速度急剧增大,负载系数越大,速度增大现象越明显,且中心层的速度相对变低, 边界层的速度则有增大的趋势。

图2 不同负载系数下的流场分布Fig.2 Flow field distribution under different load coefficients
当k 为0.83,B 分别为1.0 T 和0.5 T 时,近壁面y=0.119 与中心层y=0 的磁流体速度分布如图3 所示(图中,x 轴表示沿通道速度入口到出口的距离,0.0 m 处为速度入口,0.6 m 处为速度出口)。由图3 可以看出,当B=1.0 T 时,边界处的射流现象更加明显, 增加磁场强度可以提高边界处的最大射流速度。 对比近壁面与中心层的速度分布可以看出:在发电通道有效段入口处,中心层的速度迅速下降,近壁面的速度急剧增加;经过发电通道有效段时,由于受到洛伦磁力的影响,中心层的速度减小,近壁面的速度增大;靠近发电有效段出口处,中心层的速度继续缓慢下降,近壁面的速度急剧增加。从图3 还可以看出,近壁面处的磁流体在有效发电区间的入口速度和出口速度快速增加,并在有效发电区间x=0.4 m 附近达到最大值,而中心层的速度则相反。 由此表明, 在x=0.4 m 附近,速度剖面的波动程度比较大。通道内部的射流现象表明了液态金属磁流体发电通道内部的诱导磁场会改变流场的分布。

图3 不同磁感应强度下近壁面与中心层的速度分布Fig.3 Velocity distribution near wall and central layer under different magnetic field intensity
当磁流体发电机外接负载时, 依据数值模拟数据以及式(5),(6)可以得到如图4 所示的电流和电压随负载系数的变化情况。从图4 可以看出,随着负载系数的增加,电压也逐渐增加,而电流则逐渐减小,这一现象与理论分析相符合。这也充分表明,合理提高电压可以有效提高发电性能,但负载系数的选定还需要结合其他条件进行综合考虑。
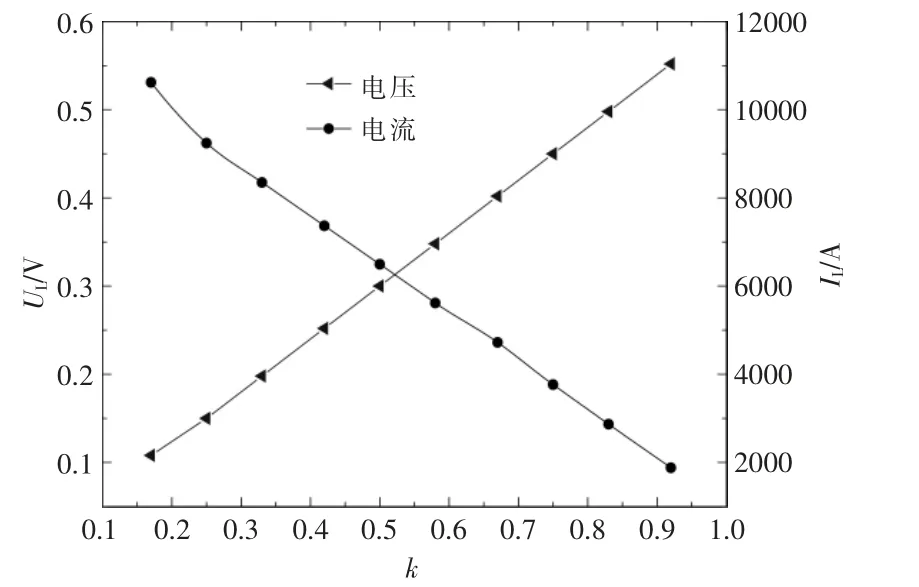
图4 电流和电压与负载系数的关系Fig.4 Relationship between current voltage and load factor
根据数值模拟数据和式(7)可以得到如图5所示的发电通道输出功率和负载系数的关系图。从图5 可以看出;当负载系数约为0.5 时,输出功率取得最大值,最大值约为1.9 kW;当负载系数超过0.5 后,随着负载系数的增加,输出功率有逐渐减小的趋势。
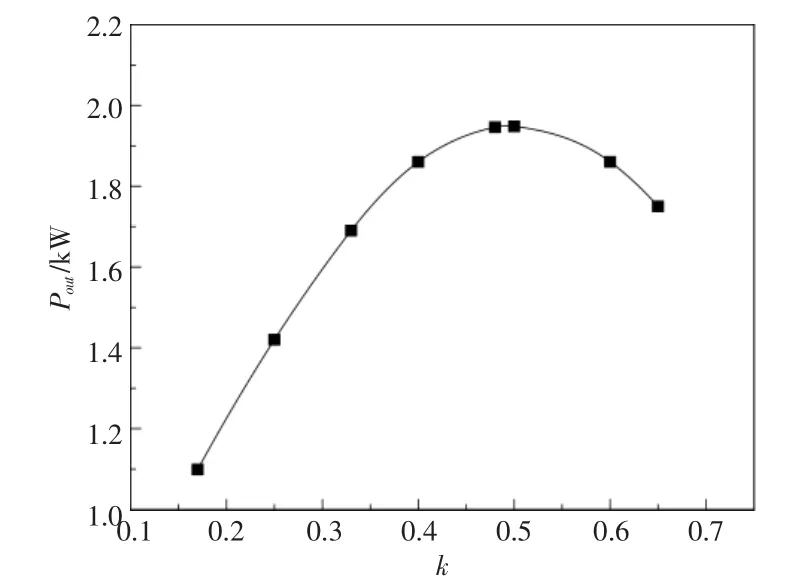
图5 输出功率与负载系数的关系Fig.5 Relationship between output power and load factor
根据数值模拟数据以及式(9),可以得到如图6 所示的发电通道发电效率与负载系数的关系图。 从图6 可以看出,随着负载系数的增加,发电效率先增大后减小, 并在k=0.67 附近取得最大值,最大值为29.2%。
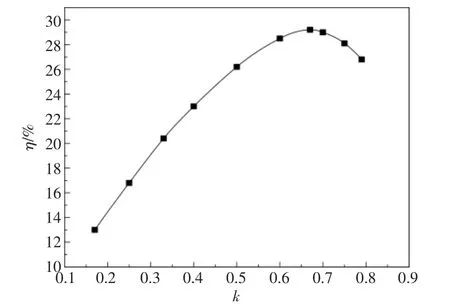
图6 发电效率与负载系数的关系Fig.6 Relationship between power generation efficiency and load factor
由图5,6 可知,当负载系数k=0.5 时,输出功率达到最大,而发电效率在k=0.67 附近取得最大值。 从图2,3 可知,负载系数越大,发电通道内部磁流体速度的射流现象越明显,越不利于发电机的发电性能。 因此,经过综合考虑,笔者认为在负载系数k=0.6 附近, 液态金属磁流体发电通道的发电性能可达到最好。
2.3 感应电动势
设定通道宽度d 和入口速度为定值,外加磁感应强度为变量,以此来研究外加磁感应强度变化对发电通道感应电动势U 的影响。 当d=0.24 m,ν=5 m/s 时, 外加磁感应强度与感应电动势的关系如图7 所示。从图7 可以看出,感应电动势随着外加磁感应强度的增大而增大, 两者呈现出正比例关系。 这一变化规律与理论计算的结果基本保持一致,但是,随着外加磁感应强度的增加,实验值与理论值的差值也越来越大。 这是因为随着外加磁感应强度的增大, 由此产生的诱导磁场的强度也随之增大, 而诱导磁场又会对电场产生干扰,造成感应电动势的增幅减小。考虑到工程实际情况以及实验室的实验条件, 可取到的最大磁感应强度为0.8 T。

图7 感应电动势与外加磁感应强度的关系Fig.7 Relationship between induced electromotive force and applied magnetic field strength
设定通道宽度和外加磁感应强度为定值,入口速度为变量, 以此研究入口速度变化对感应电动势的影响。当d=0.24 m,B=0.5 T 时,入口速度与发电通道感应电动势的关系如图8 所示。

图8 感应电动势与入口速度的关系Fig.8 Relationship between induced electromotive force and inlet velocity
从图8 可以看出:随着入口速度的增大,感应电动势近似呈线性增加;当ν>7 m/s 时,感应电动势增加的趋势有减缓的倾向。 这表明当入口速度过大时,会造成感应电动势的增加幅度减小。从图8 还可以看出,随着入口速度的增大,实验值与理论值的差值也逐渐增大。在实际工程中,磁流体通过发电通道时的速度越快, 对产生感应电动势越有利,但是,当磁流体的速度超过最适速度之后,这种有利的作用将会减弱。在实际工程中,入口速度越大,需要的成本以及所造成难度都会增大。因此,本文选取ν=7 m/s 作为优化后的入口速度。
当ν=5 m/s,B=0.5 T 时,发电通道感应电动势随通道宽度变化的规律如图9 所示。 从图9 可以看出:随着通道宽度的增大,感应电动势近似呈线性增加, 但是增加的幅度逐渐减缓, 当通道宽度d>0.9 m 时,感应电动势实验值趋于稳定;通道宽度越大,实验值与理论值的差值也越大。在实际工程中, 可通过不断增大通道宽度来增加感应电动势,但是,感应电动势增加的趋势会不断减弱,同时通道宽度的增加会增加材料费用。因此,通道宽度的选取需要综合考虑。 结合入口速度和外加磁感应强度, 本文选定d=0.9 m 作为优化后的通道宽度。
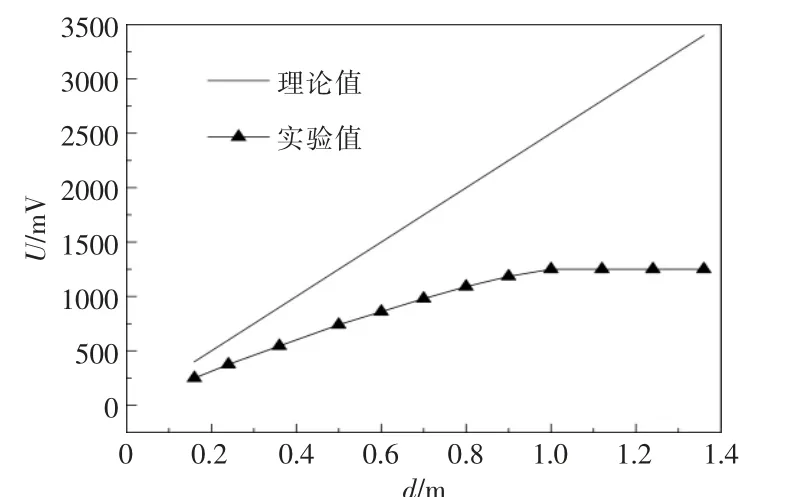
图9 感应电动势与通道宽度的关系Fig.9 Relationship between induced electromotive force and channel width
3 结论
①在不同负载系数下, 发电通道内磁流体速度变化的规律是相似的, 均存在经过有效发电段时,边界层速度急剧增大的现象;负载系数越大,边界层速度增大的现象越明显, 且中心层的速度相对变低,边界层的速度则有增高的趋势。
②当外接负载时,随着负载系数的增大,外电压呈线性增长的趋势,电流呈线性降低的趋势;输出功率和发电效率均随着负载系数的增大呈现出先增大后减小的变化趋势;发电效率在k=0.67 附近取得最大值,约为29.2%;输出功率在k=0.5 附近取得最大值,约为1.9 kW。
③随着入口速度、 磁感应强度和通道宽度的增大,感应电动势均有增大的趋势,但增大的趋势会逐渐减小。 在已有设计的基础上对发电通道参数进行优化,最后得到的最优参数为ν=7 m/s,B=0.8 T,d=0.9 m。
