基于张量SOM 和VAE 的多风电时空功率日场景生成
2022-12-27缪书唯梁云嫣
李 丹, 王 奇,2, 缪书唯, 梁云嫣,2
(1. 三峡大学 电气与新能源学院, 湖北 宜昌 443002; 2. 新能源微电网湖北省协同创新中心, 湖北 宜昌443002)
0 引言
在“双碳”目标成为国家战略的时代大背景下,作为低碳、环保的可再生能源,风力发电在总发电量中占比不断提高。 然而,风电所具有的波动性和不确定性严重影响电力系统稳定运行和电网安全,克服这些挑战的关键在于如何准确地描述风电出力不确定性。 多风电场时空功率本质上是具有时空相关性的多维随机变量,针对多风电场时空功率不确定性的场景分析方法,可以通过构建确定性场景来分析风电的不确定性。 该方法成为解决含可再生能源的电力系统规划和优化运行问题的一种有效途径[1]~[3]。
研究人员一般采用统计学方法建立风电出力场景模型, 将风电出力不确定性假设为一个统计学模型, 采用历史数据建立符合风电出力分布规律的概率模型, 并结合抽样方法随机生成出力场景样本。 文献[4]利用Wasserstein 概率距离指标分别与改进的K-medoids 聚类算法对功率概率分布曲线进行处理得到场景集, 再应用聚类的方法构造覆盖整个调度区间的经典场景集。 文献[5]采用改进的马尔科夫链模型生成日前型初始场景集, 并通过基于Wasserstein 概率距离的场景约简0-1 规划模型,应用于时序性电力系统场景集约简。 以上传统统计学模型的难点在于如何针对风电出力不确定性建立合适的概率模型, 它们多用来描述单特征时序场景的不确定性, 仅适于某一地点或系统聚合后总风电出力场景的生成。 由于多风电场的场景生成问题涉及到复杂的时间-空间相关性,因此是有待深入研究的难题。
文献[6]建立以多元正态分布函数和Copula函数为基础的风功率时空相关性模型, 并结合蒙特卡洛抽样引入Copula 理论中的条件分布,生成大量具有时空相关性的风电场景。然而,真实的风电功率数据可能并不服从多元正态分布[7], 选择合适的Copula 函数是准确描述随机变量间相关性的关键和难点[8]。随着深度学习技术的发展, 利用神经网络描述风电出力不确定性, 在一定程度上能够解决概率分布建模困难的问题, 但传统的监督学习模型难以对概率分布进行拟合,并且对训练数据量有较高的要求。无监督学习的生成模型迅速发展有望解决该问题。 生成模型在训练过程中就能够学习输入数据的概率分布, 并模拟生成服从该数据概率分布的新样本。 文献[9]中风光电出力随机场景生成方法采用条件变分自编码器, 场景生成过程完全依靠数据驱动, 无需概率建模就能够找出给定观测数据内部的统计规律。 以无监督训练方式学习得到数据样本的概率分布,且生成的数据在保证多样性的同时,能很好地反映实际日场景功率数据的时空特性[10],[11]。 文献[12]提出一种计及气象因素差异的模块化去噪变分自编码器多源-荷联合场景生成模型,对多源-荷数据进行聚类,并采用去噪变分自编码器实现不同类别下多源-荷场景生成。 文献[13]~[15]均是采用条件生成对抗网络来学习风电出力的时间-空间相关性。 判别器损失函数利用Wasserstein 距离来衡量样本集间分布差异,能够有效精确地生成可再生能源日前场景集。
在深度学习方面, 现有多源-荷场景生成方法往往忽略了时空功率相关性的多样性。 不同日场景样本中源-荷功率的时空相关性可能存在较大差异,如果不加区别的统一建模,会导致场景生成模型无法覆盖全部的功率时空相关性情景,影响场景生成的多样性。 另外,现有方法均将样本场景中的时空功率统一变换为一维向量处理后建模,导致其模型无法准确反映原始功率在时间和空间维度上的真实分布关系,影响了场景生成的准确性。
针对现有场景生成方法存在的问题以及变分自编码器在场景生成方面的优异性能,本文提出了一种基于张量距离的自组织映射神经网络(Self-Organizing Map,SOM)和变分自编码器神经网络(Variational Auto-Encoder,VAE)相结合的场景生成方法,实现多风电场时空功率日场景的随机生成。 首先,基于功率日场景的时空二阶张量距离,对历史时空功率日场景样本集聚类,以保证同一聚类簇中的日场景样本具有相似的时空相关性;然后,对各簇日场景集合分别构建VAE 编码解码网络,实现日场景内高维的实际时空功率和服从独立正态分布的低维隐含特征之间的双向变换;再对隐含特征进行独立多维正态分布的随机抽样,解码得到各簇日场景生成样本;最后,按比例将各簇日场景生成样本集合加以聚合,得到与原数据具有相似概率分布和时空相关性规律的新场景集合。 本文以某地18 座风电场多风季和少风季的风电功率数据为实际算例,验证了所提场景生成方法的有效性。
1 基于张量距离的SOM 神经网络数据聚类
1.1 张量距离
张量距离是一种衡量高阶数据对象之间相似度的度量方式。张量距离与欧氏距离的不同之处,在于它将数据不同坐标之间的位置关系考虑在内, 来有效度量高阶张量空间中数据对象之间的距离[16],[17]。

式中:glm为度量系数;G 为度量矩阵,表示多阶数据之间不同坐标的位置关系。
glm的定义如下:

当G 为单位阵I 时,张量距离等同于欧氏距离。
1.2 张量距离SOM 神经网络数据聚类
SOM 神经网络是由输入层和输出层 (竞争层)组成的无监督竞争式学习神经网络。 SOM 神经网络通过提取输入数据中的主要特征或内在规律进行分类[18]。
采用SOM 神经网络对多风电场时空功率日场景进行聚类,如式(4)所示。 风电功率实际为时间维度和空间维度上的二阶张量X∈Rm×h,其中,m 为风电场个数,h 为日内时刻点数。
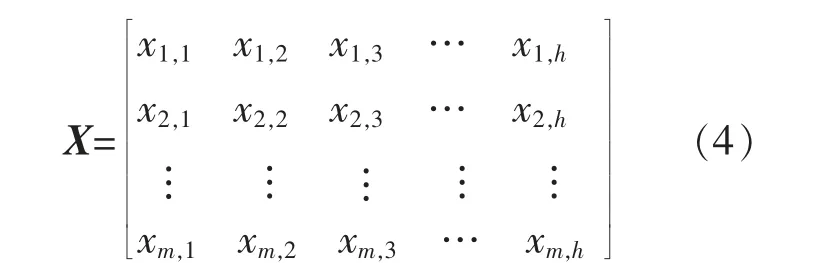
现有的多风电场时空功率日场景生成方法往往将其按行或列向量化为时空功率一维向量x∈Rm×h, 以便用欧氏距离来描述日场景两两样本之间的相似性。 从式(4)的两种向量化展开式(5)和(6)可以看出,这种数据类型的转化容易造成日场景功率数据原有的数据结构被破坏, 导致丢失日场景功率数据元素之间的时空位置关系。
按行向量化:
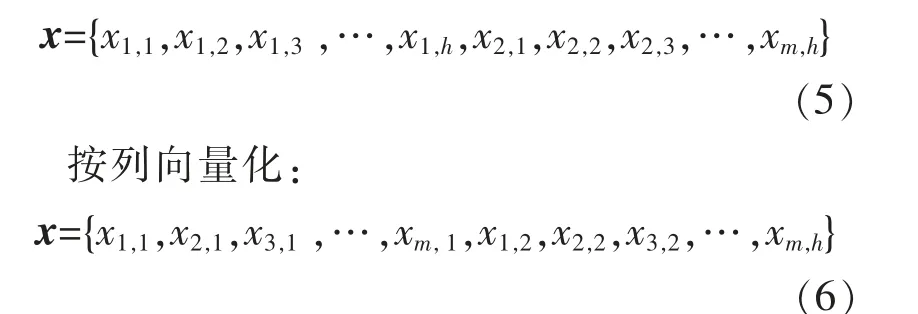
由此可见, 采用欧氏距离进行计算的弊端在于无法同时保留时空功率在时间和空间维度上的真实分布, 导致以此为基础构建的聚类或生成模型无法同时准确表征功率的时间和空间分布。 反观张量距离, 它通过与元素位置距离相关的度量矩阵G 来体现日场景矩阵数据之间的时空位置关系,使得数据之间的时空分布特征得以保留。本文针对基于欧氏距离SOM 聚类方法面临的不足,提出了基于张量距离度量的SOM 神经网络数据聚类方法,以更好保留数据之间的时空分布特征。设多风电场时空功率历史样本数据集聚类为K类,基于张量距离SOM 聚类的实现步骤如下。
①设置网络参数。对输出层各个节点权重Wj(j=1,2,…,J)赋予初值,初始化学习率α(t),设置训练结束条件。
②求取获胜节点。 求xi(i=1,2,…,n)与Wj(j=1,2,…,J)距离最短的连接权重向量:

③规定获胜单元的邻近区域N*j(t),对邻近区域内所有的单元进行权重调整, 调整过程如式(9)所示。
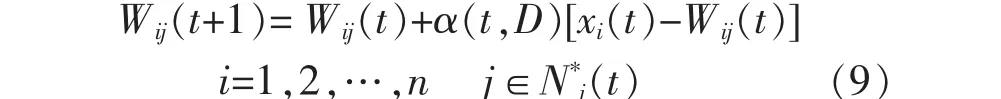
式中:α(t,D)为训练次数t 和邻域内第i 个神经元与获胜神经元j*之间拓扑距离D 的函数,α(t,D)=α(t)e-D,e-D为高斯函数。
④训练中重复步骤②,③。 当达到训练结束条件α(t)≤αmin时,停止训练;αmin为学习率最小值。
⑤输出原始数据归属的聚类类别{Ii}Ni=1(Ii∈{1,2,…,K})和K 个聚类中心C=(C1,C2,…,Ck)。
2 变分自编码器VAE
变分自编码器 (Variational Auto-Encoders,VAE) 是基于自编码器演变而来的一种数据生成模型[19]。 它作为生成模型可以在模型训练之后直接利用其解码器自动模拟生成与训练数据概率分布相似的输出。
VAE 网络由编码器和解码器两部分构成。 编码器作为识别模型qφ(z│x)对输入的样本数据编码,生成与其对应的隐变量z;解码器作为生成模型pθ(x│z)由一系列隐变量z 解码得到观测数据x˜。
为了解决隐变量z 的分布不可直接观测的问题,VAE 在识别网络中采用标准正态分布的识别模型qφ(z│x)来代替无法确定的真实后验分布pθ(x│z)。定义识别模型qφ(z│x)作为VAE 的识别网络部分,条件分布pθ(x│z)作为生成网络部分。 利用KL 散度来衡量识别模型qφ(z│x)和真实后验分布pθ(x│z)拟合的相似程度。 因此,VAE 的损失函数L(θ,φ,x)的完整计算式如下:

式中: 前项表征隐含变量z 的概率分布与先验分布qφ(z│x)的相似性,两者概率分布越相近,KL 散度越小;后项表征重构样本与原始样本间的误差。
在VAE 网络的训练中,其训练目标追求重构样本与原始样本之间的重构误差最小,且隐含变量z 的概率分布尽可能接近先验分布, 例如标准正态N(0,1)。
3 多风电场时空功率日场景生成步骤
设多风电场时空功率历史样本数据为{xi}Ni=1(xi∈Rm×h)。其中:N 为历史样本天数;m 为风电场个数;h 为日内时刻点数,设h 为24。 本文场景生成模型的基本流程如图1 所示。
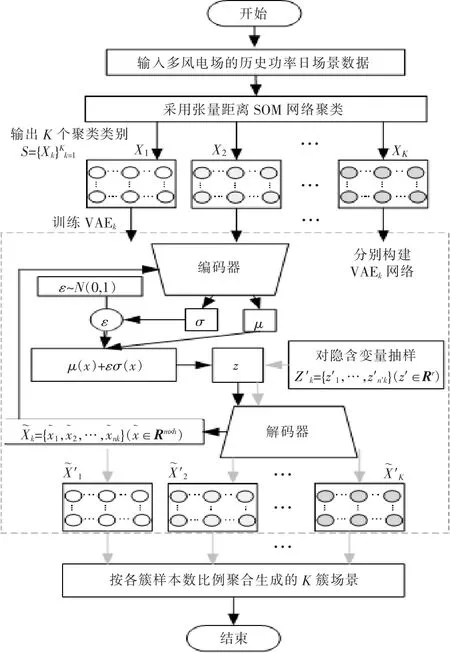
图1 场景生成流程图Fig.1 Scene generation flowchart
场景生成模型的实现步骤如下。
①采用张量距离SOM 神经网络对历史样本日集合进行聚类, 得到聚类簇S={Xk}Kk=1,Xk=(x1,x2,…,xnk)。 其中:nk为第k 簇风电功率数据的样本数;K 为聚类簇个数。
②分别对K 个聚类簇构建VAE 变分自编码网络,并基于各聚类簇场景样本集Xk无监督训练各簇对应的VAEk网络(k=1,2,…,K):
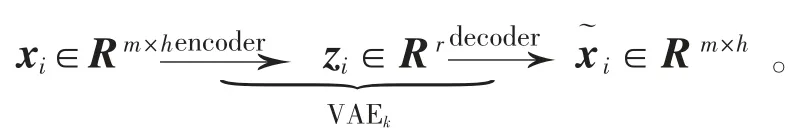
VAE 的编码器将输入的样本场景xi∈Rm×h降维,提取出r 个(r<<mh)具有标准正态分布且相互独立隐含变量, 组成特征向量zi∈Rr。 将zi作为VAE 解码器的输入,亦可解码为重构场景x˜i∈Rm×h。 各VAEk网络基于对应聚类簇中场景样本数据进行无监督训练,得到最优的模型参数。
③基于训练好的VAEk模型,遍历K 簇,随机采样生成各簇日场景样本集合。
设生成的总场景数为M, 对第k 簇, 基于VAEk模型,独立抽样出n′k=Mnk/N 个服从标准正态分布的隐含变量样本, 组成r 维隐含特征向量样本集合Z′k={z′1,z′2,…,z′n′k}(z′∈Rr) ,输入对应簇的VAEk解码器, 重构为第k 簇的生成日场景

4 算例分析
4.1 算例介绍
为了更好地验证场景生成的有效性, 须要选取具有完整季节周期性的历史风电功率数据。 本文以某地区18 座风电场2016 年风电功率作为数据样本 {xi}366i=1,(xi∈R18×24), 数据间隔取1 h,共8 784 组多风电场功率数据,每组数据均为实测出力。将全年8 784 h 的18 座风电场总功率,通过风电场的出力判断实际风资源季节性分布情况,将6-10 月份划为少风季, 其余月份划为多风季,训练前对数据集进行预处理, 剔除偏差过大的错误数据,并对数据集进行归一化处理。将本文所提张量距离SOM 聚类结合VAE 生成方法(方法1)与欧氏距离SOM 聚类结合VAE 生成方法 (方法2)、不聚类直接应用VAE 生成方法(方法3)进行对比。 所有程序用matlab2019a 编写,在Intel(R)Core(TM)i5-8400 CPU@2.80GHz 计算机运行。本文方法和对比方法的参数设置见表1。
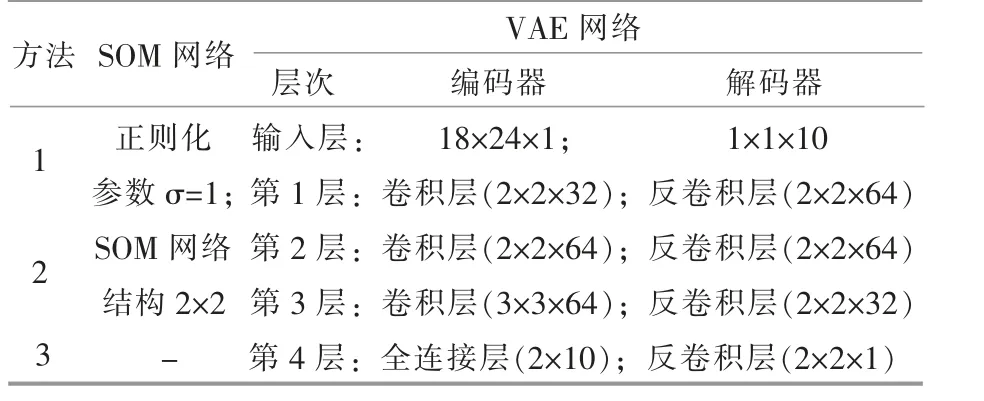
表1 3 种方法参数设置Table 1 Parameter setting of three methods
4.2 结果分析
在未知实际标签信息的情况下, 采用轮廓系数(Silhouette Coefficient,SC)作 为 选 定 最 优 聚类数评估标准。 根据专家经验,聚类数为K∈[2,10]。

式中:b 为该样本与其他簇样本间最小平均距离;a 为该样本与簇内样本平均距离。
SC 的取值为[-1,1],SC 越大表示聚类质量越好。 本文采用所有日场景的平均SC 作为评估聚类结果的指标。 图2 所示为K=2~10 的SC 指数。 结果表明,K=4 时日场景类型聚类效果最合适。
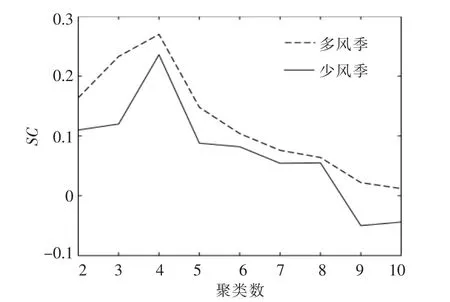
图2 不同聚类数下的SC 值Fig.2 SC value under different number of cluster
(1)基于不同距离度量方式的聚类结果对比
方法1 和方法2 将多风季和少风季的日场景数据聚成4 类。 图3 给出了两种方法聚类结果中各簇样本数所占比例。
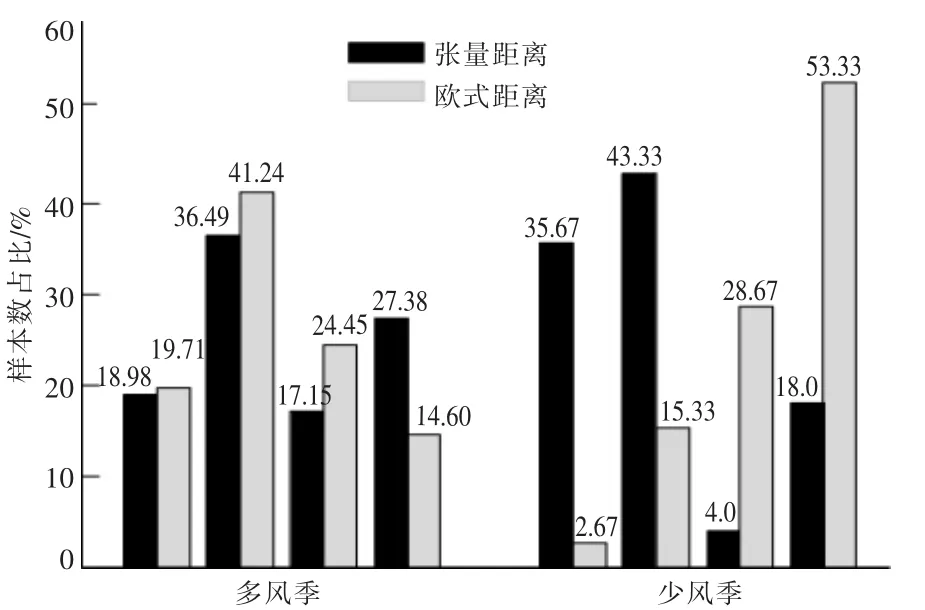
图3 两种聚类方法各簇样本占比对比情况Fig.3 Comparison chart of the proportion of each cluster sample between the two clustering methods
从图3 可以看出, 基于不同距离度量方式的两种聚类方法, 获得的每个聚类簇所占原场景总数的百分比不同。由此可见,当选用不同距离度量标准时,对SOM 聚类结果影响较大。
对两种聚类方法的性能进行对比, 采用内部评价指标DB(Davies-Bouldin Index)指数度量每个簇类最大相似度的均值[20]:
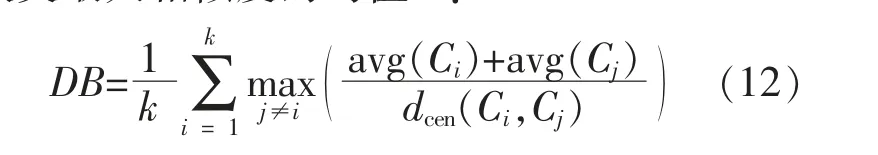
式中:avg (C) 表示簇C 内样本间的平均距离;dcen(Ci,Cj)对应于簇Ci和簇Cj中心点间的距离。
DB 指数越小,说明聚类效果越好。
经计算, 基于张量距离聚类和基于欧氏距离聚类的DB 指数在多风季分别为0.75 和2.23;在少风季分别为0.66 和2.32。 整体上张量距离的DB 指数更低, 表明张量距离SOM 神经网络聚类方法能获得类间相似度更小、 信息更加多样化的聚类结果,提高聚类结果的多样性和准确性。
(2)聚类对生成场景重构MAPE 误差的影响
用平均绝对百分比误差MAPE 计算VAE 网络生成的重构场景与原始场景之间的重构误差:式中:Pj为第j 座风电场的额定功率。
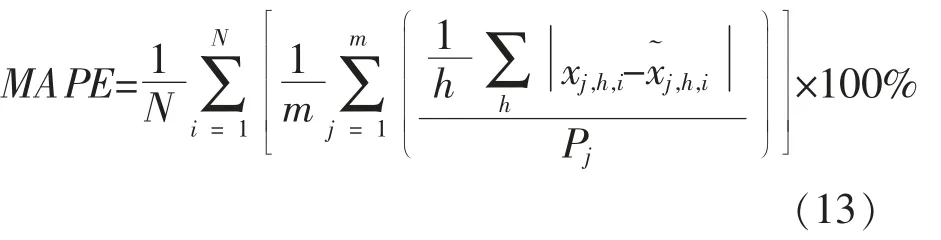
方法1 和方法3 的重构误差MAPE 对比如图4 所示。 由图4 可见,采用张量距离SOM 进行聚类的4 个聚类簇生成数据MAPE 整体都小于未经聚类直接VAE 结果的MAPE。将4 个聚类簇的平均绝对百分比误差按样本占比权重求出重构误差MAPE 值, 多风季为5.27%, 少风季为4.05%, 分别比未经聚类直接VAE 方法的MAPE值降低了8.87%,10.1%。

图4 聚类与未聚类生成场景的MAPE 误差对比Fig.4 Comparison of MAPE error between clustered and un-clustered generated scenarios
(3)生成场景的时空相关性误差对比
为进一步验证本文方法生成场景对功率时空相关性特征提取的有效性, 分别计算多风季和少风季原场景空间和时间线性相关性系数矩阵、3 种方法生成场景的时空相关系数矩阵和原场景之间的绝对误差。 可视化热力图如图5 所示。

图5 3 种方法生成场景的时空相关系数绝对误差对比Fig.5 Comparison of spatio-temporal correlation errors of the three methods
图5(a)和图5(b)显示多风季的空间和时间相关性误差;图5(c)和图5(d) 显示少风季的空间和时间相关性误差。 从图中颜色的深浅可以看出, 经聚类后生成场景的空间和时间相关性误差在整体上都要小于未经聚类的相关性误差。
本文方法多风季的空间和时间平均误差分别为0.023 和0.025,相比方法2,3 的空间相关性误差分别降低了0.007 和0.147;本文方法多风季的时间相关误差比方法2 高0.001,但比方法3 降低了0.195;本文方法少风季的空间和时间平均误差均为0.011,比方法2,3 的空间和时间相关性误差分别降低了0.013 和0.152,0.015 和0.261。 本文方法的相关系数误差总体上最小, 表明本文方法生成的场景能更准确反映原始场景的时空相关性规律。与基于欧氏距离聚类的场景生成方法相比,在少风季本文方法的改善作用更显著。
(4)生成场景的累积概率分布误差分析
原始场景和3 种方法生成场景中计算各时刻18 座风电场的平均功率之后,将全部平均功率的经验累积概率分布对比如图6 所示。

图6 3 种方法生成场景平均功率的累积概率分布Fig.6 Cumulative probability distribution of the three methods
从图6 中多风季和少风季两种情况下3 种方法累积概率分布对比可以看出,在概率分布方面,3 种方法均表现较好, 以无监督的形式实现了传统场景生成方法中概率建模的效果。 本文方法生成场景与原始场景最为接近。
图7 为多风季和少风季的原始场景与3 种方法模拟生成场景在相同经验累积分布下所对应的功率误差图。 本文方法在多风季和少风季时的平均绝对误差分别为0.33 和0.43,相较于方 法2,3 分 别 降 低 了0.02 和2.19,0.06 和0.54。 由此可见,采用本文方法模拟生成的场景与原始场景的功率数据误差最小。 这验证了本文方法能更准确地捕获历史风电功率数据的概率分布规律。
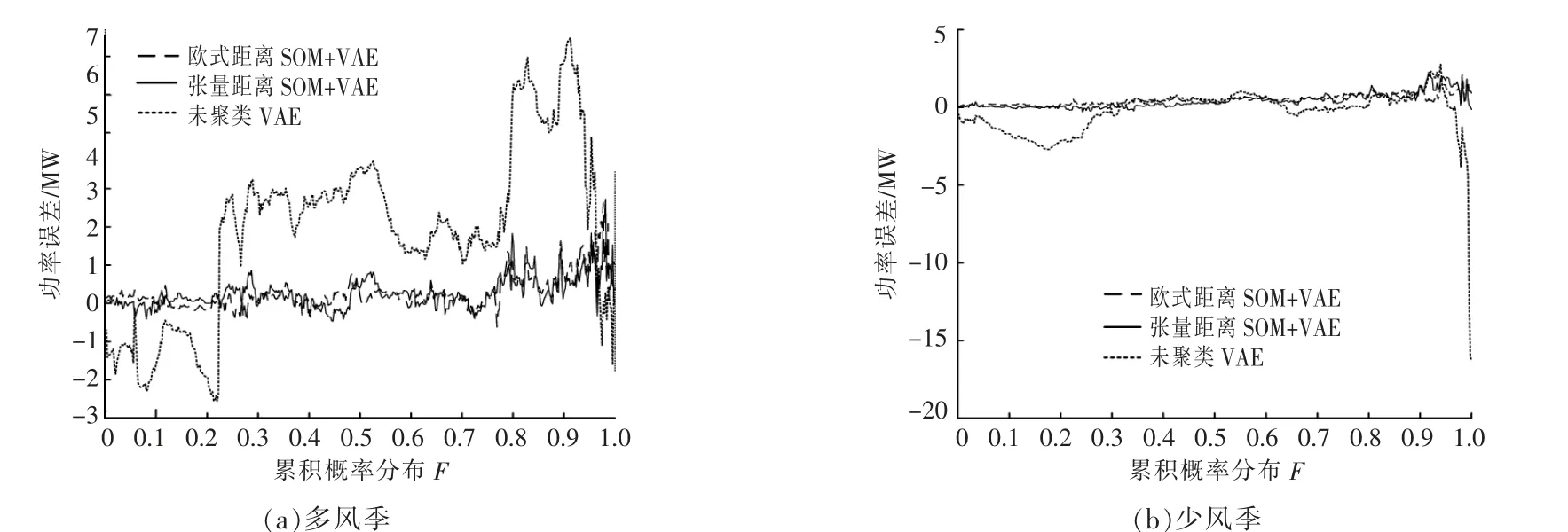
图7 3 种方法生成场景与原场景在相同经验累积分布下所对应功率误差对比Fig.7 Comparison of the power errors between the three methods and the original scene under the same empirical cumulative distribution
5 结论
为解决现有场景生成方法无法准确、全面反映原始场景中功率时空分布关系的问题,本文提出了一种张量SOM 神经网络聚类和VAE 变分自编码器降维相结合的多风电场时空功率日场景生成方法。 通过实际算例表明,该方法具有以下特点。
①相较于传统欧氏距离SOM 聚类方法,张量距离SOM 聚类通过引入日场景矩阵中数据之间时空位置关系的权重矩阵, 能更准确地反映风电功率在时间或空间维度上的真实分布, 从而获得类间相似度更小、信息更加多样化的聚类结果,从而提高聚类结果的多样性和准确性。
②在构建生成网络模型之前, 先将具有相似时空相关性的日场景历史样本聚合, 能有效提高生成网络的训练效果和降低重构误差, 提高生成网络的精度和生成场景的多样性。
③与传统欧氏距离SOM 聚类方法和不聚类直接VAE 方法相比,本文方法可显著降低生成场景风电功率的空间和时间相关性误差, 提高概率分布特征的准确性, 强化场景生成方法的特征表达能力,在少风季的改善效果更为显著。
