基于双采样的LCL 型并网逆变器并网电流间接控制研究

张具琴， 贺素霞， 马 康， 刘威龙

（1.黄河科技学院 工学部， 河南 郑州 450063； 2.中科（洛阳）机器人与智能装备研究院， 河南 洛阳 471003）

0 引言

分布式发电系统的发展给电网带来了灵活的调度，同时也给微电网的电压质量带来了一定的考验[1]～[3]。并网逆变器将分布式发电系统中的直流电转换为交流电汇入电网时具有频率不等的谐波分量，尤其因为高频动作的开关器件而引起的高频谐波较为严重。 因此，并网逆变器需要配置滤波器滤除高频分量，LCL 型滤波器较LC型滤波器具有较强的高频谐波滤除能力，而得到了广泛使用[4]，[5]。

LCL 型滤波器的低频段与LC 型几乎一致，但高频段的谐波滤除能力远远高于LC 型。 LCL型并网逆变器是一个三阶系统，可能会引起谐振效应，导致系统不稳定，因此谐振抑制问题是必须要解决的。 LCL 谐振抑制方法可以分为无源阻尼法和有源阻尼法两大类。 其中：无源阻尼法通过在LCL 型滤波器的元件上串联或者并联电阻以实现阻尼[6]，无源阻尼法因为能量损耗常常不被单独使用；有源阻尼法通过控制方法抑制谐振，不会对系统产生损耗。 文献[7]提出基于电容电流反馈法的有源阻尼方法来抑制谐振。 文献[8]提出通过电容电压计算电容电流的方法，从而抑制谐振效应。文献[9]通过对三阶的LCL 型滤波器系统进行降阶，提出将滤波电容按比例进行拆解的方法。文献[10]提出一种逆变器侧电流和电网侧电流双闭环的控制方法来抑制谐振效应。

本文在逆变器侧电流反馈作为并网电流间接控制方法的基础上，通过推导占空比表达式，直接推导出以逆变器侧电流为控制对象， 同时以电容电压反馈为谐振效应抑制的控制方法。 所提方法减少了传感器个数， 基于正序分量提取的锁相环技术能够精确地获取电网电压相位信息， 使得LCL 型并网逆变器稳定运行，谐振效果得到抑制。

1 LCL 型滤波器结构

图1 为三相LCL 型滤波器的拓扑结构。 LCL型滤波器由滤波电感Lx1，Lx2以及滤波电容Cfx组成，同时将Lx1称为逆变器侧电感，电感上电流ix1称为逆变器侧电流，将Lx2称为电网侧电感，电感上电流ix2称为电网侧电流。 vx为逆变器输出电压，Lgx为电网电感，vgx为电网电压，其中，x=a，b，c。

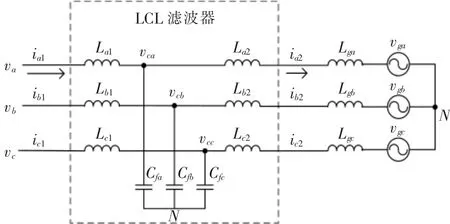
图1 三相LCL 型滤波器的拓扑结构Fig.1 Topology diagram of three-phase LCL-type filter

如图2 所示，无源阻尼法通过在LCL 型滤波器的滤波元件上串联或者并联电阻以实现阻尼的效果，显然这种方法会对系统产生损耗，因此无源阻尼法通常不被单独使用。 而有源阻尼法是在无源阻尼法的基础上，通过状态变量的反馈，在效果上等效为无源阻尼法，但是不会产生损耗。

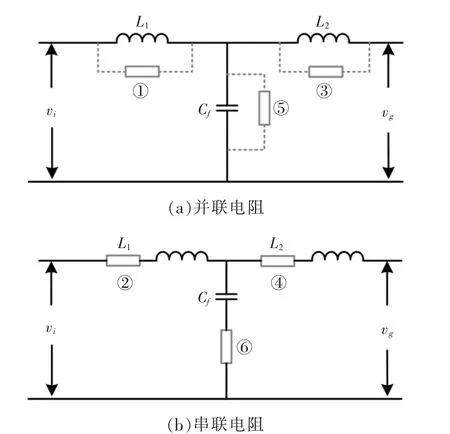
图2 6 种无源阻尼法Fig.2 Six passive damping methods

可以推导出单相LCL 型并网逆变器的控制框图，如图3 所示。 为了方便传递函数的推导，将变量中的x 全部剔除，以此代替单相的系统。

图3 单相LCL 型并网逆变器控制框图Fig.3 Control block diagram of single-phase LCL-type gridconnected inverter

根据图3 中的控制框图， 能够推导出以逆变器侧电流为控制目标的s 域传递函数为

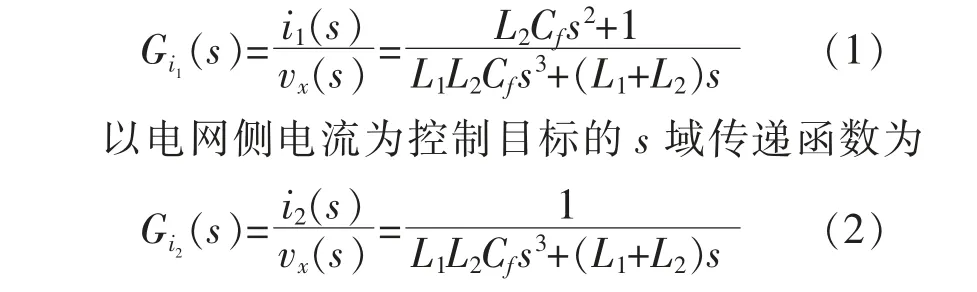
根据式（1），（2）中的传递函数可以绘制出系统的Bode 图，如图4 所示。从图中可以看出，系统存在正负谐振峰，会导致系统不稳定。

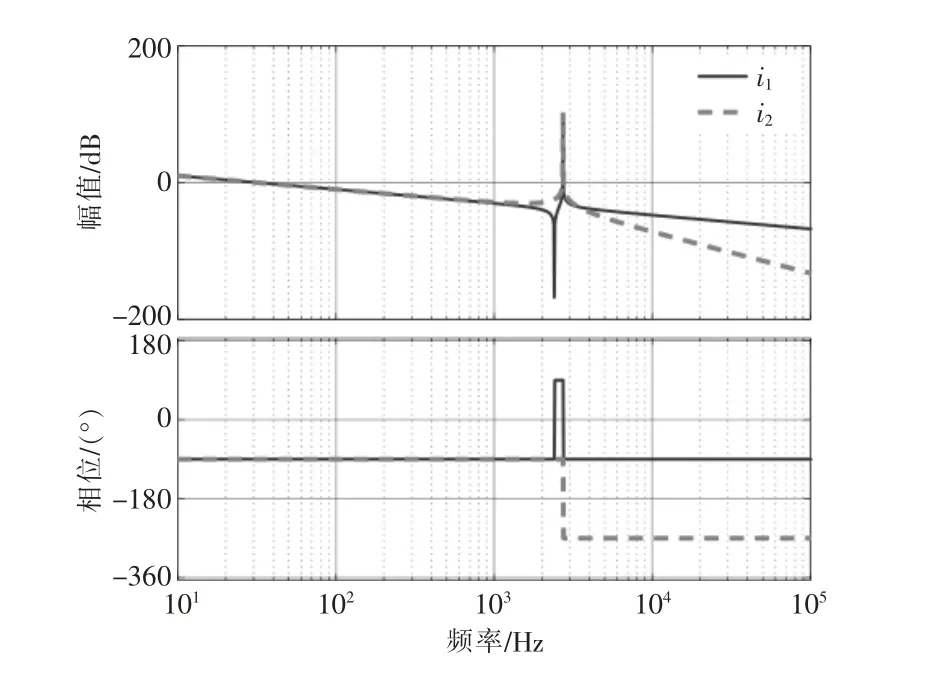
图4 系统Bode 图Fig.4 Bode diagram

当LCL 型滤波器的电感参数发生变化时，绘制不同参数下的Bode 图，如图5 所示。 从图中可以看出，当电感值发生变化时，谐振频率会左移，意味着谐振频率的降低。

2 并网电流间接控制算法

根据图1 所示的拓扑结构， 考虑电网电感为0 的情况下， 可以列出三相静止abc 下的数学模型为

一般情况下，由于开关频率远远大于50 Hz，因此可以利用前向差分法对式（5） 进行整理，得到：

式中：Ix1（n+1）为逆变器侧电流的第n+1 时刻的参考给定值。

传统的并网电流控制方法， 基本上采用坐标变换至dq 坐标系或者αβ 坐标系下进行控制。 本文的并网电流控制方法不需要坐标变换， 直接在三相abc 坐标系下完成控制，控制更加简单，无需设计控制参数。

3 电流参考值计算

在实际中，电网常会出现非理想情况，此时电网电压可以分解为正序分量UP、 负序分量UN和零序分量U0，表示如下：

式中：U 为三相电压信号。

三相电网电压可以表示为

使用PI 控制器使变换后输出的电网电压无功分量趋近于0，从而完成电网电压相位的锁定，控制框图如图6 所示。

图6 锁相环控制框图Fig.6 Phase locked loop control block diagram

在完成锁相环之后， 可以得到电网电压相位信息，之后建立电流参考信号如下：

式中：Im为电流参考给定值的幅值。

4 结果验证

为了验证本文所提方法的有效性，利用PSIM软件和如图7 所示的实验平台进行验证。

图7 实验平台Fig.7 Experimental platform

图8 为三相并网电流仿真波形，0.05 s 之前只采用逆变器侧电流控制（图中a），0.05 s 之后采用逆变器侧电流控制结合电容电压反馈控制（图中b）。从图中可看出：未采用电容电压反馈抑制谐振时，电流出现较大的谐波，系统不稳定；当采用电容电压反馈抑制谐振后，谐振效应被完全抑制。

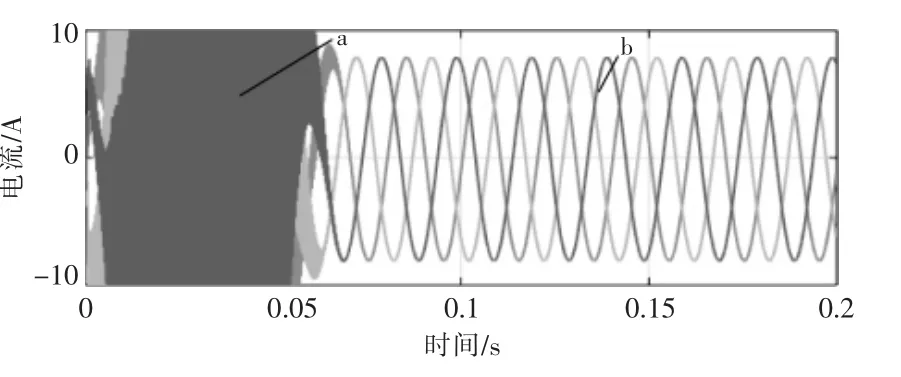
图8 三相并网电流仿真波形Fig.8 Simulation waveform of three-phase grid connected current

图9 为三相并网电流突变仿真波形。从图中可以看出，当电流给定值发生变化时，并网电流能准确快速地跟踪参考给定值。 同时，采用本文所述的控制方案，能够保证突变过程中的系统稳定性。

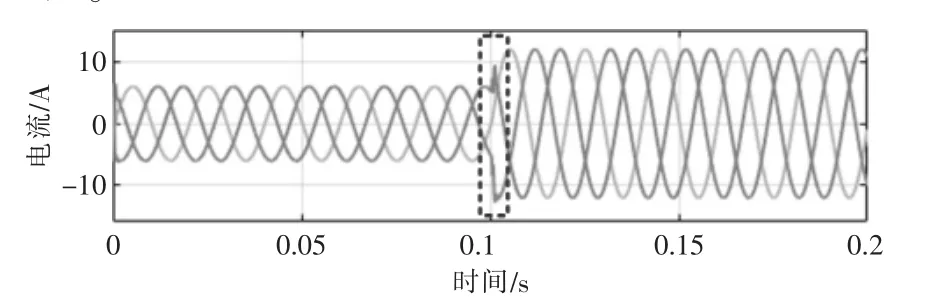
图9 三相并网电流突变仿真波形Fig.9 Sudden change simulation waveform of three-phase grid connected current

图10 为采用本文所提出的并网电流间接控制方法的三相并网电流实验波形。 从图中可以看出： 当未采用电容电压反馈时， 并网电流出现谐波，系统不稳定；采用本文的方法，并网电流能够得到很好的控制，系统稳定运行。

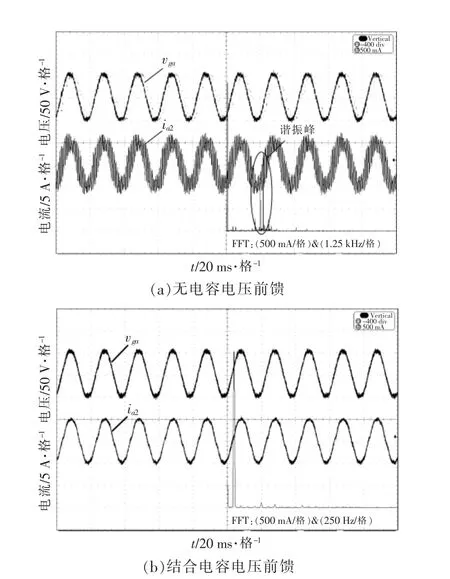
图10 三相并网电流实验波形Fig.10 Experimental waveform of three-phase grid connected current

图11 为三相并网电流突变情况下的实验波形。从图中可以看出，采用本文所述的电流控制方案，能够保证电流突变时的快速跟踪，同时保证系统的稳定性。

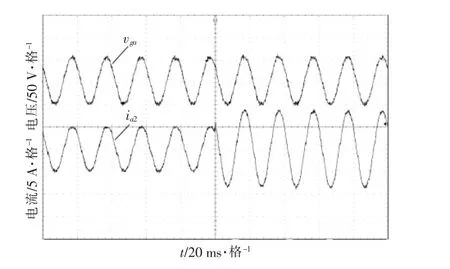
图11 三相并网电流突变实验波形Fig.11 Experimental waveform of sudden change of threephase grid connected current

5 结语

LCL 型滤波器比LC 型滤波器具有更好的高次谐波滤除能力，然而LCL 型并网逆变器存在谐振效应。 本文在LCL 型滤波器数学模型的基础上，推导出逆变器占空比表达式，同时给出基于正序分量提取的锁相环技术， 能够精确地获取电网电压相位信息，从而构建电流参考值。仿真和实验结果表明， 采用逆变器侧电流控制结合电容电压反馈这一间接并网电流控制方法， 能够很好地保证并网电流的精确跟踪，同时保证系统稳定运行。