基于驾驶行为生成机制的智能汽车类人行为决策*
2022-12-27宋东鉴韩嘉懿刘彦辰
宋东鉴,朱 冰,赵 健,韩嘉懿,刘彦辰
(吉林大学,汽车仿真与控制国家重点实验室,长春 130022)
前言
随着汽车智能化技术的不断发展,如何使智能汽车决策规划系统像人类驾驶员一样驾驶车辆已成为一项重要的研究内容[1-2]。类人决策规划能够有效提高智能汽车的社会认同度以及用户信任度和接受度,降低由人机差异造成的事故风险,对提高交通系统尤其是智能汽车与人工驾驶汽车并存的混合交通系统的安全性、协调性以及通行效率具有重要意义[3]。
智能汽车的决策规划又可进一步划分为行为决策和运动规划,行为决策层基于环境信息输出离散化的行为指令,例如车道保持(lane keeping,LK)、换道(lane changing,LC)以及加减速等;而运动规划层负责在行为决策层的指导下给出行为指令对应的具体运动轨迹。传统的非数据驱动行为决策方法包括有限状态机(finite state machine,FSM)[4]、博弈论[5]、贝叶斯网络决策[6]、模糊推理[7]等。该类方法依靠人工构建规则、机理抽象或注入专家经验等手段构建具有良好可解释性的经验或半经验策略,场景遍历广度高,但是对复杂场景理解深度不足,且先验知识难以有效覆盖驾驶行为生成机制中蕴含的隐式语义信息,在实现类人行为决策上存在原理性瓶颈。
而数据驱动方法以驾驶人数据为范本,基于学习型算法学习驾驶人特性与行为模式,在实现类人驾驶上具有天然优势。按照其实现层级的不同,数据驱动的决策规划可分为如下两类。
第1类是结果驱动型。其本质上属于结果导向而非问题导向,根本任务是基于驾驶人数据,通过直接模仿学习[8-9]或自学习[10-12]等方法建立起从客观世界到驾驶人行为之间的黑盒映射模型,在结果级实现对驾驶人行为的复现。但结果驱动型存在“知其然,不知其所以然”的问题,策略可解释性和泛化性等仍待提升。
第2类是特征驱动型。这是一种问题导向的策略,通常假定驾驶人是客观世界中,具有某种理智思考范式和一定随机不确定性的主观多目标协同优化者,其核心思想是从专家示教中推断类人的优化目标或奖励函数,在特征级实现可解释的类人驾驶,往往能够达到“知其然,且知其所以然”的效果。Xu等[13]面向换道行为构建奖励函数,使用有限内存下的BFGS算法优化奖励函数权重,实现了匹配驾驶人特性的决策规划。Silver等[14]利用最大边际规划框架学习到考虑驾驶人不同风格的成本函数,有效解决了行驶环境和驾驶偏好的耦合问题。逆强化学习(inverse reinforcement learning,IRL)近年来被广泛应用于特征驱动的类人决策规划,并被证明相比于其他多目标优化算法,IRL更善于从示教数据中恢复类人奖励函数[15-16]。Wu等[17]使用最大熵逆强化学习(maximum entropy inverse reinforcement learning,ME-IRL),通过时空解耦与弹性采样提高了ME-IRL的采样效率,实现了入环岛场景下的类人决策规划。Huang等[18]进一步将车间交互引入ME-IRL,建立了高速公路驾驶人模型。Sun等[19]基于循环神经网络估计动作奖励值,在IRL架构下实现了类人换道。
目前基于IRL的类人驾驶尚存有待探索的问题:在策略构建过程中缺少对驾驶行为机制的深入分析,奖励函数的构造缺少对驾驶人认知特性的匹配,限制了策略向机理层下探的可能;在IRL中,高维度的采样空间能够细化策略的动作输出,但过高的维度会影响策略的泛化能力且可能引发维数灾难[20];通过离散化处理能够降低采样空间维度,但过高的离散化程度则会导致采样空间难以覆盖驾驶人的真实驾驶行为,导致策略类人性不足。为解决上述问题,本文在ME-IRL基础上,提出了一种基于驾驶行为生成机制的类人行为决策策略(human-like behavior decision-making strategy,HBDS)。
本文的主要贡献可概括为:(1)分析了驾驶行为生成机制,构建了类人行为决策策略架构,并设计了能够表征驾驶人认知特性的奖励函数;(2)利用MEIRL和玻尔兹曼理性噪声模型(Boltzman noisilyrational model,BNM)建立了类人奖励与类人行为之间的量化关系,从机理层面实现了特征驱动的类人行为决策;(3)构建离散化的预期轨迹空间,基于统计学规律和安全约束进行空间压缩和剪枝,提升了策略的采样效率,并通过引入交通车轨迹预测增加策略与环境交互的真实性,提升了类人奖励函数权重提取的准确性。
1 策略架构与问题建模
1.1 驾驶行为生成机制分析与行为决策策略框架
驾驶人执行何种驾驶行为本质上是由其认知特性和行为特征决定的,如图1所示。本文将驾驶行为生成机制中蕴含的语义信息表达为:在来自人-车-环境耦合系统的复杂不确定性约束下,驾驶人根据自身认知特性,从提高通行效率、降低跟驰负荷等驱动诱因出发生成行为动机,并评估该行为的舒适性损失、需承受的风险以及对其他交通参与者的影响等可行性指标,进而择取并执行匹配自身认知特性和行为特征的驾驶行为。
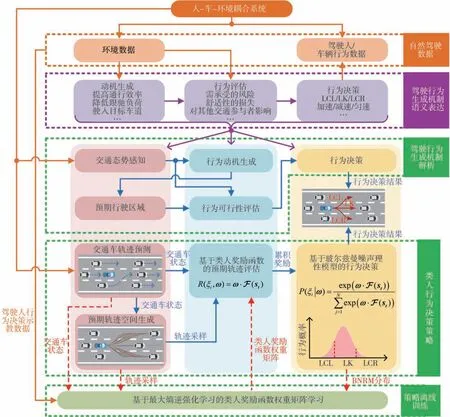
图1 基于驾驶行为生成机制的智能汽车类人行为决策抽象步骤
进一步地,可将驾驶行为生成机制解析为如下过程:(1)驾驶人接收人-车-环境耦合系统的多源信息,感知当前交通态势;(2)在交通态势刺激下生成行为动机,并在脑海中生成行为动机对应的预期行驶区域,这些区域通常包含左换道(lane changing to left,LCL)、车道保持(lane keeping,LK)、右换道(lane changing to right,LCR)以及加速、匀速、减速等驾驶行为;(3)基于交通态势评估预期行驶区域的行车风险和决策行为可行性;(4)遵从“趋利避害”的基本原则完成行为决策。驾驶人认知特性和行为特征的差异将体现在行为动机生成和行为可行性评估上,不同驾驶人在相同环境下可能产生不同的个性化行为决策。
基于对驾驶行为生成机制的语义表达和解析,本文中构建了如图1下半部分所示的智能汽车类人行为决策策略框架:(1)将驾驶人对交通态势的感知表达为对与自车(ego vehicle,EV)存在交互依赖关系的相关交通车的轨迹预测,以获取相关交通车在决策时域内的运动状态;(2)将驾驶人在脑海中生成的抽象预期行驶区域建模为由有限条预期轨迹组成的具象预期轨迹空间;(3)通过构建类人奖励函数来描述驾驶人的行为动机生成和行为可行性评估过程,HBDS从预期轨迹空间中采样,计算每条预期轨迹的累积奖励,其中奖励函数子项包含动机类和评估类两种;(4)利用BNM为各条预期轨迹分配与其累积奖励相关的被选概率,从而表征驾驶人在进行驾驶行为决策时的随机性。HBDS需基于ME-IRL进行离线训练,ME-IRL能够从自然驾驶数据中学习类人奖励函数权重矩阵,从而匹配驾驶人认知特性和行为特征,进而实现基于驾驶行为生成机制的智能汽车类人行为决策。
1.2 智能汽车行为决策问题建模
将智能汽车行为决策建模为1阶马尔可夫决策过程MDP(S,A,P,R)。其中S为状态空间,A为动作采样空间,P为状态转移概率,R为累积奖励。时间步t的状态st∈S由EV状态以及周围交通车状态组成,包含可基于现有传感技术获得的EV和周围交通车的位置、速度、加速度等基本运动学信息。如图2所示,通常认为EV的当前车道前车(currentlane front vehicle,CFV),当前车道后车(currentlane rear vehicle,CRV),左车道前车(left-lane front vehicle,LFV),左车道后车(left-lane rear vehicle,LRV),右车道前车(right-lane front vehicle,RFV),右车道后车(right-lane rear vehicle,RRV)会对EV的行为决策产生影响,因此对于该MDP,时间步t的状态st可写作:
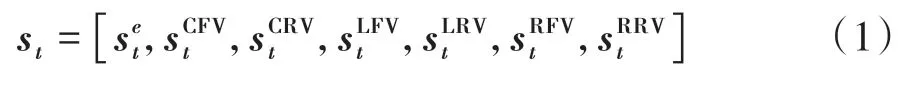
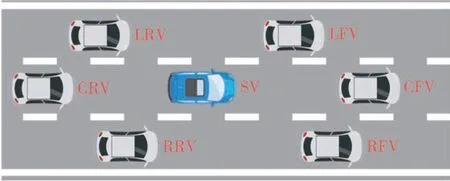
图2 影响EV行为决策的周围交通车
EV动作at所从属的动作空间A实际上即为预期轨迹空间,可理解为某条预期轨迹执行过程中须施加给车辆的纵侧向控制量。因此,一条长度为V的离散化轨迹可写成V组状态-动作对的形式:
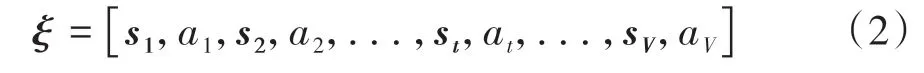
预期轨迹空间中的任意轨迹ξi均可写成式(2)的形式。而在该行为决策MDP中,除初始状态s1为已知外,其他时间步的状态均须根据预期轨迹ξi进行运动学推导或预测。对于ξi执行过程中的时间步t,EV状态可根据预期轨迹直接获取,而周围交通车的状态则须基于交通车运动轨迹预测获得。将给定st的奖励函数r(st)定义为线性结构:

式中:F(st)=[f1(st),f2(st),...,fL(st)]为状态st下的奖励函数子项向量;ω=[ω1,ω2,...,ωL]T为与奖励函数子项匹配的权重矩阵。则轨迹ξi的累积奖励R(ξi,ω)可写作:
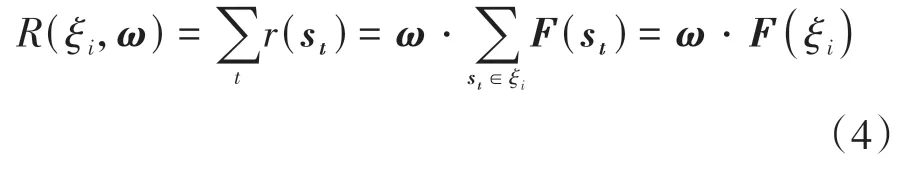
式中F(ξi)为整条轨迹的奖励函数子项向量。本文将在第3节中详述奖励函数子项的构造以及如何基于ME-IRL学习类人的权重矩阵ω。
得到ω后,便可获得预期轨迹空间中任意轨迹的累积奖励R(ξi,ω),而要想实现行为决策,还须建立预期轨迹被选概率与其累积奖励之间的映射关系。根据最大熵原理,可假定预期轨迹被选概率随其累积奖励的增加呈指数型增长,本文中基于BNM构建行为决策概率与累积奖励的映射关系[21],在给定权重矩阵ω时,预期轨迹ξi被选择的概率为
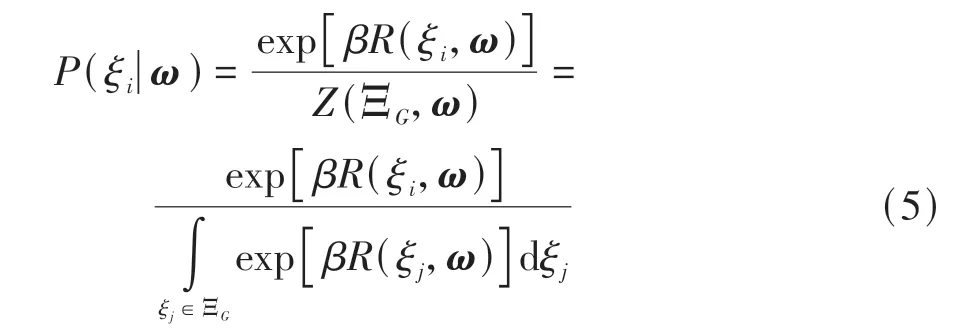
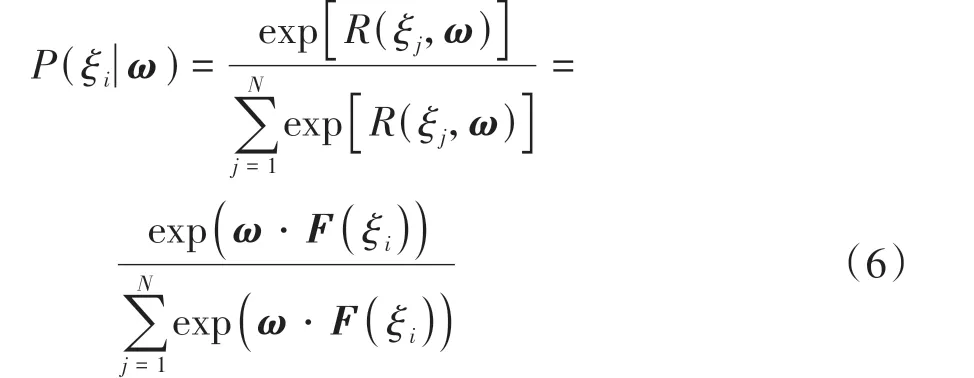
式中:N为预期轨迹空间中所包含的轨迹数量。基于式(6)可得预期轨迹中每条轨迹被选择的概率,遵循理智驾驶人“趋利避害”的原则,参考贪婪算法思想,HBDS会在每个状态下选择累积奖励最大的预期轨迹所对应的驾驶行为作为此时智能汽车的行为决策结果。
2 预期轨迹空间生成
2.1 预期轨迹空间生成
预期轨迹空间作为行为决策MDP的动作采样空间,应涵盖驾驶人在常规交通场景中的各种驾驶行为。本文使用多项式拟合和智能驾驶员模型(intelligent driver model,IDM)[22]生成包含LCL、LK、LCR这3类驾驶行为的预期轨迹簇,并对预期轨迹空间进行压缩和剪枝以提升采样效率。
2.1.1 换道预期轨迹簇生成
通常驾驶人在脑海中预规划换道轨迹时,会考虑期望车速、换道耗时等因素,为体现这些因素对换道轨迹的影响,使用多项式拟合换道预期轨迹。在全局坐标系xoy下,分别使用四次多项式和五次多项式拟合换道过程中EV纵向和侧向位置随时间的变化,即
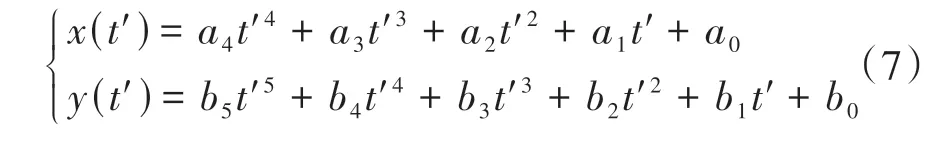
给定换道起始和终止时刻的边界条件即可求得式(7)中的系数。设换道起始时刻和终止时刻的边界条件分别为和其中,换道初始时刻的边界条件可由驾驶人示教数据中EV的初始运动状态直接获得。对于终止时刻的边界条件,通常假定换道结束后车辆已能在目标车道进行稳定的车道保持,故取,取yend为目标车道中心线的侧向位置。那么影响多项式换道轨迹拟合的变量即为换道持续时间TLC和换道终点车速,使用不同的TLC和的取值组合即可生成包含不同形状轨迹的换道轨迹簇。
2.1.2 车道保持预期轨迹簇生成
若不考虑车道保持过程中EV的侧向运动,则车道保持预期轨迹的生成实际上就是EV纵向加速度的拟合。引入IDM描述车道保持过程中EV的纵向加速度axe(t):
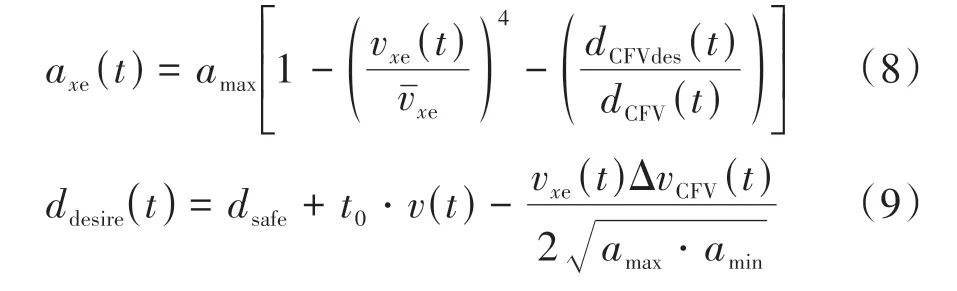
式中:vxe(t)为EV车速;vˉxe为期望速度;dCFVdes(t)为期望跟车距离。而最小安全车距dsafe,期望跟车时距t0,最大加速度amax和最大减速度amin均为可标定的常数项。EV的车道保持预期轨迹形状由期望纵向速度vˉxe和车道保持持续时间TLK决定,且为保证车道保持和换道预期轨迹累积奖励计算时的公平性,车道保持预期轨迹和换道预期轨迹共享相同的变量取值空间,即
2.2 预期轨迹空间压缩与剪枝
2.2.1 基于统计学规律的预期轨迹空间压缩
预期轨迹空间包含的轨迹数量由换道持续时间TLC和换道终点纵向速度张成的二维空间决定,为提升HBDS对预期轨迹的采样效率以及预期轨迹空间构造的合理性,对NGSIM(next generation simulation)数据集中乘用车在不同换道初始速度下的TLC以及γ进行统计分析。其中,γ为相比于的变化率,即

如图3所示,使用正态分布分别拟合TLC和γ的概率密度,μ1、μ2和σ1、σ2分别为TLC和γ正态分布的均值和方差,其取值如表1所示。
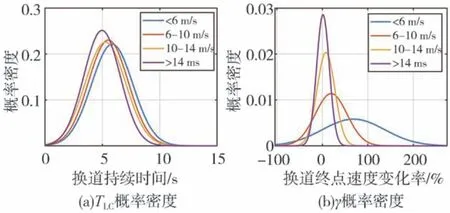
图3 不同初始速度下TLC与γ概率密度分布
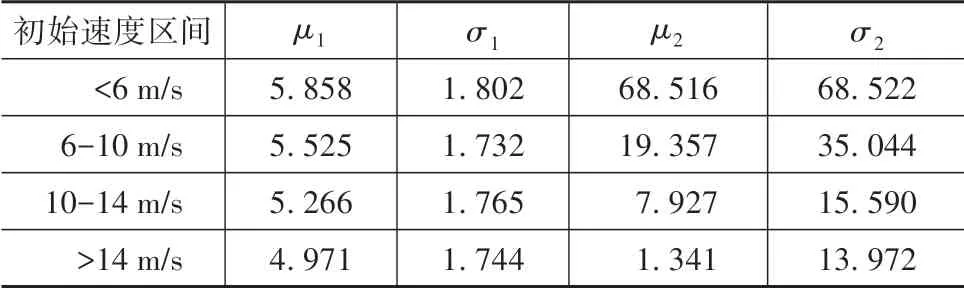
表1 正态分布参数表
由图3(a)可知,TLC的基本变化规律是换道初始速度越大,换道持续时间越短,不同换道初始速度下的TLC分布具有一定差异但并不明显,因此可将不同初始速度的TLC分布进行合并。相比之下,在图3(b)中,γ的概率密度分布对换道初始速度变化非常敏感,初始速度越大,换道终点速度变化越小且分布越集中,而当初始速度低于6 m/s时,换道终点速度普遍具有较大提升,说明驾驶人通过执行换道行为实现了较大幅度的提速。如表2所示,基于概率密度分布,本文为不同换道初始速度下的TLC和γ划定取值区间,并给出取值粒度。因此根据驾驶人示教数据的初始状态,可以为预期轨迹空间匹配不同的边界与大小,提升策略采样效率的同时使预期轨迹更接近驾驶人轨迹。
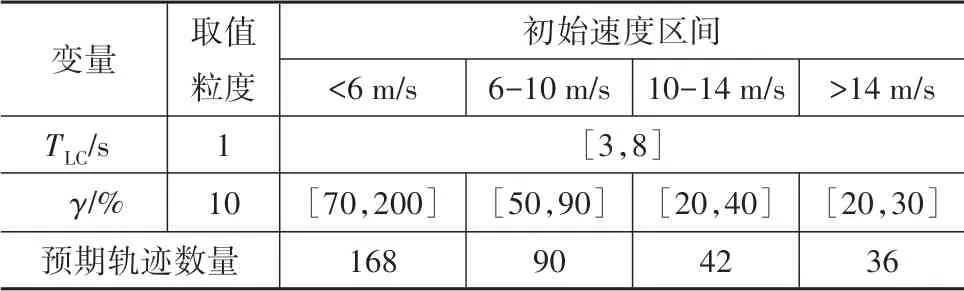
表2 TLC和γ取值区间与粒度
2.2.2 基于安全约束的预期轨迹空间剪枝
在上述预期轨迹空间基础上,对不符合安全性和动力学约束的预期轨迹进行剪枝。首先对所生成轨迹进行基于几何轮廓的碰撞检测,去除掉所有发生碰撞的轨迹;其次,评估所规划轨迹的纵、侧向动力学稳定性,给定纵向加速度极限[-0.8μg,0.8μg]以及侧向加速度极限[-0.3μg,0.3μg],去除所有超出上述极限,可能引发车辆失稳的轨迹。图4给出了按照NGSIM数据集中某次驾驶人换道的初始状态所生成的预期轨迹空间。假定路面附着状态良好,取路面附着系数μ为0.8。
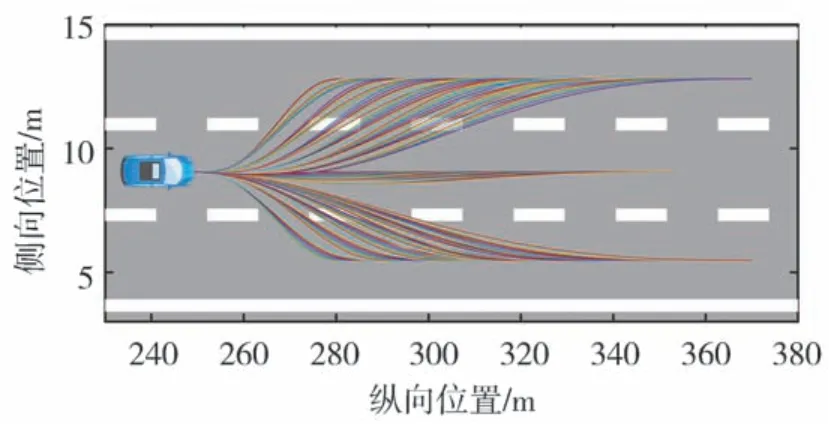
图4 压缩与剪枝后的预期轨迹空间
3 面向行为决策的交通车轨迹预测
预期轨迹累积奖励R(ξi,ω)的计算需要已知周围交通车的运动状态,若ξi的执行不会对交通车运动状态产生影响,则其运动状态可直接从自然驾驶数据中获取,否则须预测ξi执行过程中交通车如何运动。为此本文构建了可同时预测周围6台交通车未来轨迹的预测模型,模型结构如图5所示。在当前时刻t,模型的输入序列X和输出序列Y分别为
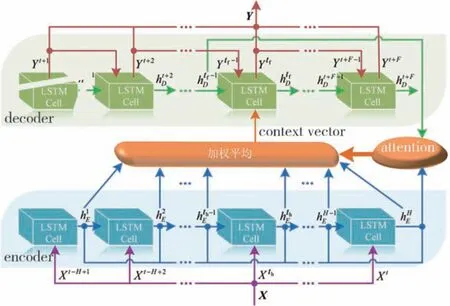
图5 交通车轨迹预测模型结构
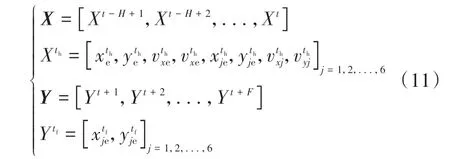
式中:H和F分别为历史时窗和预测时窗长度,取H为6 s,而为匹配不同的预期轨迹长度,根据表2,F取为3~8 s。xe、ye和vxe、vye分别为全局坐标系下EV的纵侧向位置和纵侧向速度,xje和yje分别为交通车j相对EV的纵侧位置,vxj和vyj分别为交通车j的纵侧向绝对速度。
如图5所示,交通车轨迹预测模型使用了具有注意力(attention)机制的编码器(encoder)-解码器(decoder)结构。在每个编码时间步th,encoder的每个LSTM cell接收来自前一编码时间步的隐状态和当前编码时间步的输入,输出当前编码时间步的隐状态,直至将整个输入序列X编码为语义向量(context vector)。与encoder结构基本相同的decoder接收语义向量,并在每个解码时间步tf输出6台交通车的轨迹预测值,直至完成整个预测时间窗F上的交通车轨迹预测。
此外,在每个解码时间步tf,attention机制通过计算decoder在上个解码时间步的隐状态和encoder隐状态序列之间的相关性,为不同编码时间步的encoder隐状态分配权重,进而通过加权求和得到语义向量。attention机制的引入使轨迹预测模型能充分提取输入序列X中的时空依赖特征,提升轨迹预测精度。模型基于NGSIM数据集进行训练和测试,表3给出不同F下,测试集上的轨迹预测均方根误差RMSE。
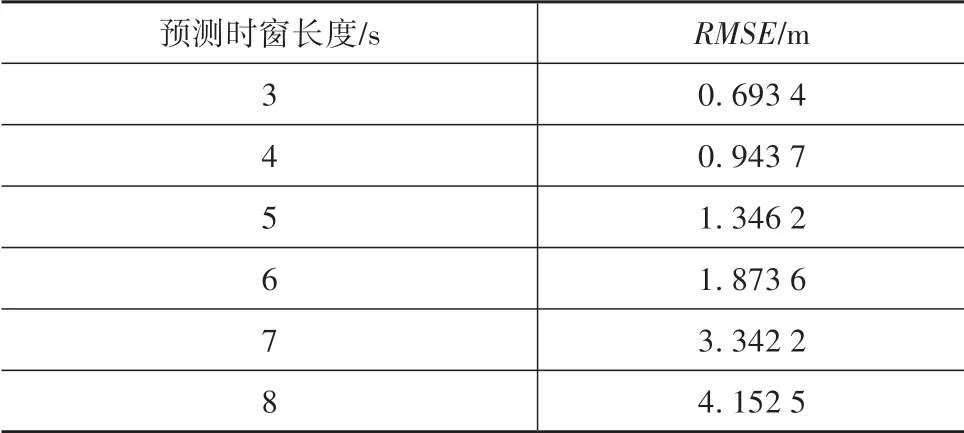
表3 不同预测时窗长度下的RMSE
从表3可知,交通车轨迹预测误差随时间的累积效应较明显,尤其是F=7~8 s时,RMSE值较大。但考虑到HBDS中交通车的轨迹预测是为表征驾驶人对交通态势的认知,最终目标是进行行为决策,而非规划EV的具体运动轨迹,因此对预测精度要求并不高,表3中的精度已可满足本文的研究需要。
4 基于ME-IRL的类人权重矩阵离线学习
如第1节所述,HBDS实现类人行为决策的关键在于构建匹配驾驶人认知特性的类人奖励函数,本节将详述奖励函数子项的构造以及ME-IRL如何学习奖励函数类人权重矩阵。
4.1 奖励函数构造
奖励函数是沟通客观环境与驾驶人主观认知的关键。基于对驾驶行为生成机制的解析,将奖励函数划分为两大类:一是动机型奖励,对应于驾驶行为动机生成过程,是驾驶人短暂观察交通环境后即可明确的奖励,本质上属于驾驶行为的驱动诱因;二是评估型奖励,对应于驾驶行为可行性评估过程,需要驾驶人对交通态势和驾驶行为的执行过程进行综合分析,本质上属于驾驶行为的限制条件。对于任意轨迹ξ,各奖励函数子项如下。
(1)通行效率 代表驾驶人对尽可能高效快速行车的期望,可用EV与跟驰对象的车速差表征。通行效率属于动机型奖励,是刺激驾驶行为产生的驱动诱因,定义为

式中:ΔvCFV(t1)和ΔvTFV(t1)分别为初始状态下EV与CFV和 目 标 车 道 前 车(target-lane front vehicle,TFV)的速度差。如果不存在CFV或TFV,则fEff(ξ)可近似为当前车道限速值与自车速度的差值。
(2)跟驰负荷 代表驾驶人跟驰前车过程中的驾驶负荷,Balal等[7]指出,相比于速度或跟车时距等参数,驾驶人在跟驰过程中往往对车距的敏感性更高,跟驰负荷也很大程度上由车距决定。跟驰负荷属于动机型奖励,是刺激驾驶行为产生的驱动诱因,例如当驾驶人观察到旁车道前车与EV具有更大的纵向车距可供EV加速或进行更加轻松的跟驰时,驾驶人往往会换至旁车道。跟驰负荷定义为

式中dCFV(t1)和dTFV(t1)分别为初始状态下EV与CFV和TFV的纵向车距。如果不存在CFV或TFV,则fLoad(ξ)取为d0,d0为驾驶人在正常能见度下的平均可视距离,高速公路场景下通常取d0=150 m[23]。
(3)舒适性 属于评估型奖励。驾驶人在产生行为动机后会评估该驾驶行为执行过程中的舒适性损失。车辆的变速运动会影响驾乘舒适性,因此通过预期轨迹的纵向加速度axe和侧向加速度aye来描述舒适性:
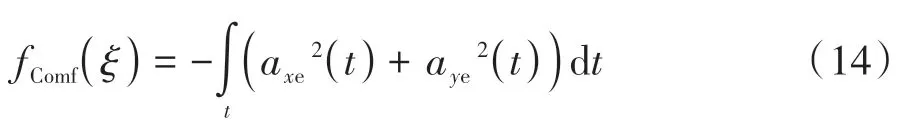
(4)行车风险 属于评估型奖励。安全是一切驾驶行为顺利执行的先决条件,因此行车风险是驾驶人评估某驾驶行为即某预期轨迹是否可行的关键因素。驾驶人在评估风险时,会综合考量周围相关交通车的位置、车速、运动趋势以及与EV之间的交互关系,故驾驶人对行车风险的认知是连续且动态,仅使用跟车时距、碰撞时间等离散化指标难以对其进行准确描述。
为此,通过构建各向异性行车风险场来描述周围交通车施加给EV的风险。对于轨迹ξ中的任意时间步t,EV周围某交通车j在EV处产生的风险场场强Eje(t)定义为
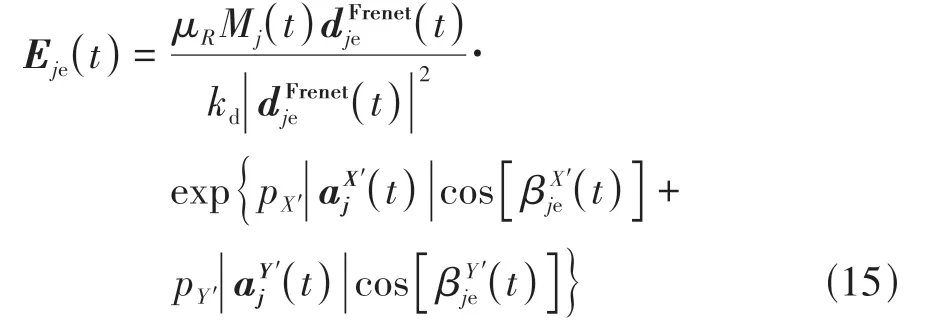
式中:(t)为在交通车j的Frenet坐标系下,EV与交通车j之间的车距矢量;kd为车距放缩因子;(t)和(t)分别为交通车j沿其前进方向的加速度和法向加速度;μR为风险场的场强峰值,场强峰值出现在交通车j的质心位置(t)和(t)分别为d(t)与交通车j前进方向和法向的夹角;pX′和pY′为加速度系数。Mj(t)为交通车j的等效质量,即
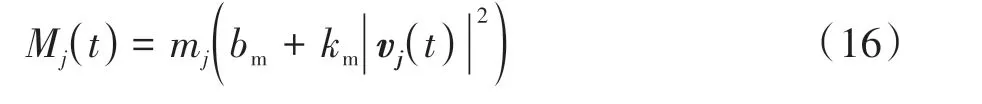
式中:mj和vj(t)分别为交通车j的真实质量与车速矢量;bm和km为常数项。通过引入固连在交通车j上的Frenet坐标系,同时实现了场强Eje沿交通车j前进方向和法向的非对称分布,并考虑了加速度大小和方向对场强分布的影响,形成了风险场的各向异性。
图6给出本文所建立的行车风险场场强分布,可以看到该风险场模型能有效表征交通车在周围环境中产生的风险分布,且能通过场强形状的变化反映交通车加减速以及换道对风险分布的影响:加速行驶的车辆在其车头前方产生的场强大于后方;减速行驶的车辆在其车尾产生的场强大于前方;左换道和右换道车辆则在其法向加速度方向上呈现出更大场强,基本符合驾驶人对风险的认知特性。
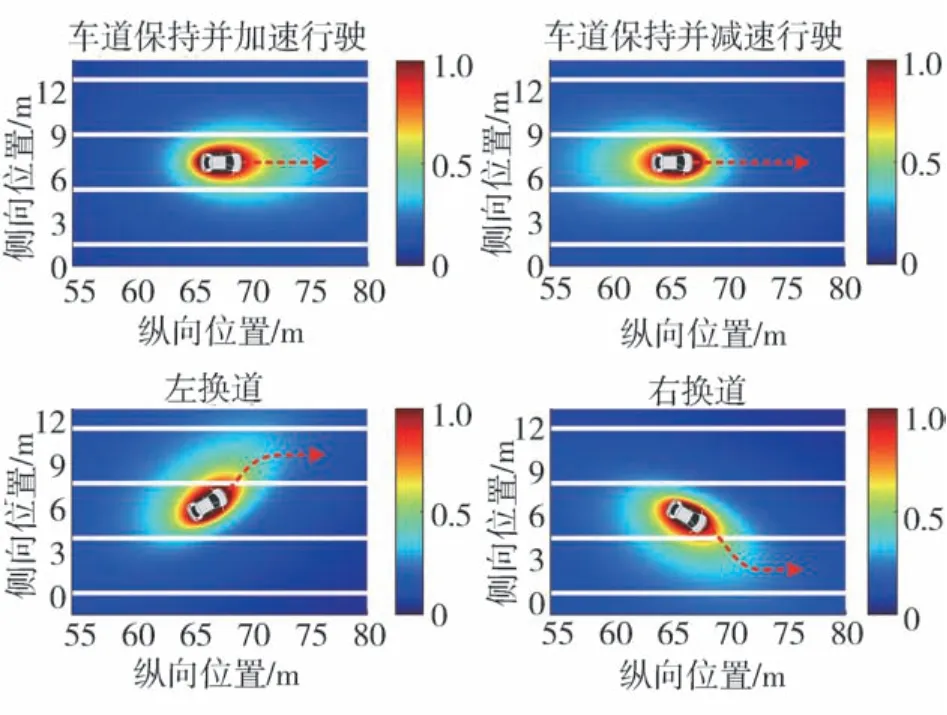
图6 不同运动状态的交通车风险场场强分布
驾驶人对风险的认知除具有连续性外,还具有截断性,即如果交通车施加给EV的场强值低于某一阈值,驾驶人会认为该交通车不会对EV产生安全威胁,据此驾驶人对行车风险的认知可描述为
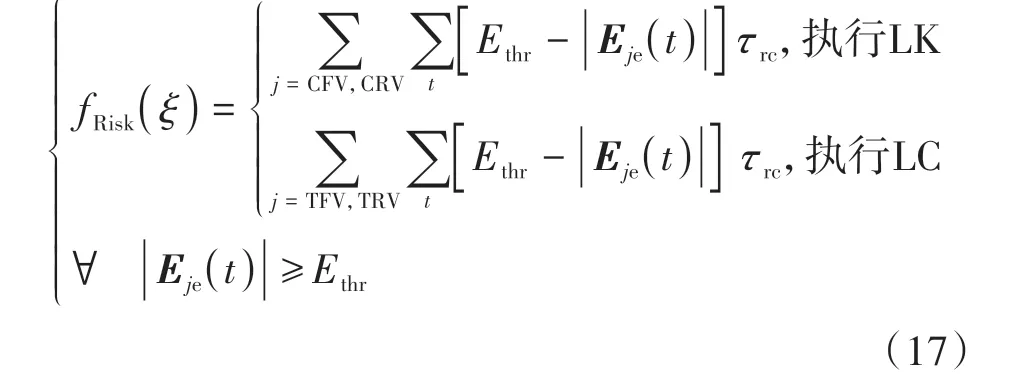
当EV执行LK时,由于车道线对场强的截止效应,EV受到的风险主要来自于CFV和CRV;当EV执行LC时,驾驶人则主要关注来自目标车道前车TFV和 目 标 车 道 后 车(target-lane rear vehicle,TRV)。式(17)中,Ethr是驾驶人不会对风险做出响应的临界场强,τrc为风险超过阈值的持续时间。故如图7所示,fRisk(ξ)实际上表征的是ξ执行过程中,驾驶人感知到的对行车安全有威胁的风险在时间上的积分。
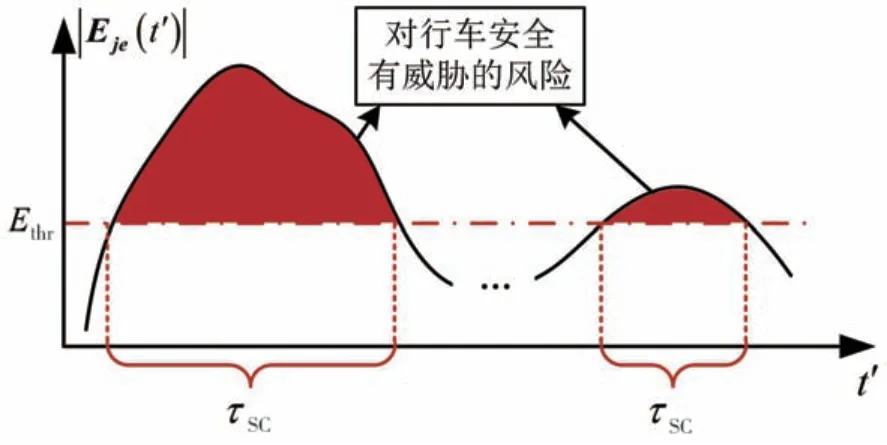
图7 fRisk(ξ)的构造原理
(5)行车侵略度 属于评估型奖励。理智型驾驶人尤其是较为礼貌友好的驾驶人在行为决策时通常会考虑EV的行为对周围交通车产生的影响,本文定义行车侵略度对其进行描述。交通车因EV的行为而产生的额外驾驶响应是EV对该交通车侵略度的显式体现,例如TRV因为EV的cut in行为而减速避让,这种驾驶响应来源于EV施加给交通车的风险,本质上属于一种风险响应。故参考对EV行车风险的建模,行车侵略度可定义为
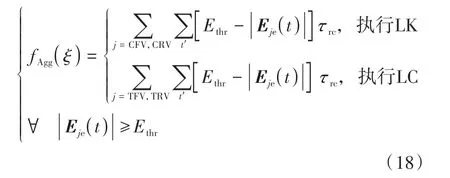
式中Eje(t)为EV施加给交通车j的场强,其计算公式与Eje(t)相同。
将式(12)~式(14)、式(17)~式(18)代入式(4)即可得轨迹ξ的累积奖励R(ξ,ω)。上述奖励函数子项能够同时描述驾驶行为生成机制中的动机生成和行为评估,并考虑车间交互,在奖励函数构造上实现了对驾驶人认知特性的匹配。
4.2 最大熵逆向强化学习
设ΞD为从自然驾驶数据中提取的驾驶人行为决策示教轨迹数据集,ΞD中包含M条示教轨迹,ΞD=[ξ͂1,ξ͂2,...,ξ͂M]。则ME-IRL的目标即是通过求解权重矩阵ω,使示教轨迹获得的累积奖励最大。由式(6)可知,累积奖励最大意味着轨迹被选择的概率最大,也就意味着HBDS能够以最大的概率做出类人的行为决策。示教轨迹中关于权重矩阵ω的对数似然函数为
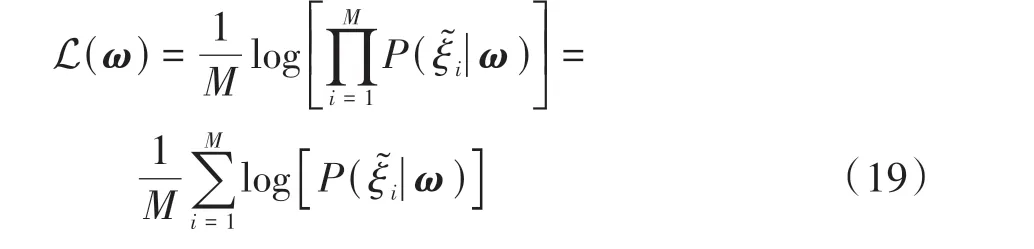
则ME-IRL对最优ω*的求解可描述为

将式(6)代入式(19)可将L(ω)进一步写作:
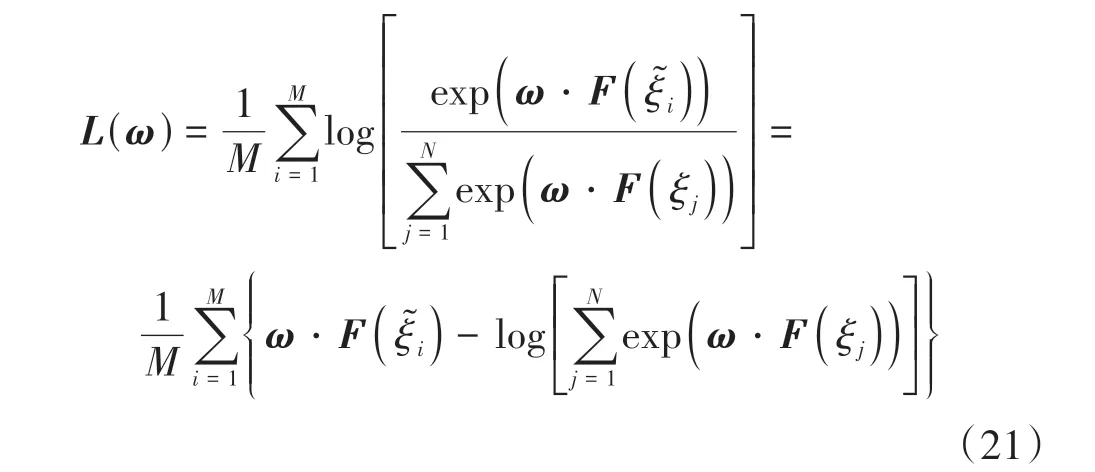
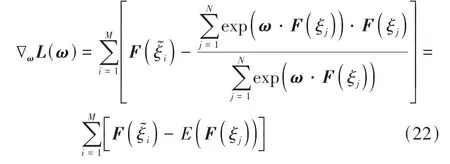
式中E(F(ξj))为整个预期轨迹空间奖励函数的期望值,因此∇ωL(ω)可视为驾驶人示教轨迹奖励与预期轨迹簇期望奖励的差值。基于式(22)使用梯度上升算法即可实现对ω的迭代优化,从而基于ME-IRL学习到对于HBDS而言最优的权重矩阵ω*。
5 策略验证与结果分析
5.1 驾驶人示教数据提取与处理
使用NGSIM数据集进行HBDS的训练和测试。NGSIM[24]由美国联邦公路局采集,包含在公路I-80和US-101上于不同时间段采集的数据,数据采集时长共90 min,采样周期为0.1 s,包含这期间出现在两条道路上所有车辆的基本信息。NGSIM中每辆车的平均持续行驶时间为40~70 s,基本符合提取驾驶人认知特性和行为特征对数据长度的需要。本文中对NGSIM数据集的处理过程如下。
(1)提取同时包含LK和LC行为的车辆。
(2)上下匝道不属于本文研究内容,且驾驶人在匝道区域的认知特性和行为特征相比常规路段会发生变化,会对驾驶行为的学习产生影响,因此本文去除涉及汇入及驶出匝道区域和存在明显误差的数据。
(3)使用Savitzky-Golay滤波器对原始数据中的车辆位置进行滤波处理,并基于滤波后的位置数据求取速度和加速度信息。
(4)按照驾驶行为将每辆车的数据划分为换道数据和车道保持数据:
①对于LK数据,提取持续时间5 s的LK行为,并要求其在LK开始前3 s和结束后3 s范围内无LC行为,采用滑动时窗提取LK数据;
②对于LC数据,按照文献[25]中方法提取LC起始点和终止点,在换道起始点处向前扩展3 s的LK数据,将其与换道起始点和终止点之间的数据一起组合为完整的换道行为数据。
NGSIM中的每辆车平均可提取出30~50组数据,每辆车均按照80%和20%的比例划分训练集和测试集。
(5)驾驶人轨迹数据规则化处理。在自然驾驶数据中,由于驾驶人的操作随机性以及数据采集误差,驾驶人轨迹往往难以与多项式和IDM生成的预期轨迹相匹配,这会造成策略训练过程中难以收敛。因此本文根据驾驶人轨迹实际的初始状态、终止状态及持续时间,对驾驶人轨迹进行基于多项式的规则化处理。图8为驾驶人轨迹经规则化处理后的效果。
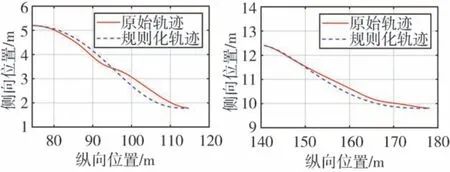
图8 驾驶人轨迹规则化处理
5.2 策略验证
5.2.1 行为决策结果
考虑到不同驾驶人认知特性和行为特征差异造成的驾驶行为生成机制异质性,使用每位驾驶人的数据分别训练个性化的HBDS。当HBDS在测试集上运行时,它会基于学习到的类人奖励函数权重计算每个初始状态下每条预期轨迹的累积奖励,并依据式(6)所示的BNM得出每条预期轨迹的被选概率。由于在生成预期轨迹时,LCL、LK、LCR 3类驾驶行为包含的轨迹数量相等,因此所包含轨迹的被选概率之和最高的那一类行为即为此时行为决策结果。
(1)为验证本文引入各向异性行车风险场的有效性,建立了对比策略HBDS-TTC。该对比策略使用车间的碰撞时间(time to collision,TTC)代替式(17)和式(18)中的各向异性行车风险场场强。除行车风险奖励函数和行车侵略度奖励函数外,HBDSTTC的其他奖励函数子项以及策略架构、训练和测试数据等均与HBDS保持一致。表4给出了HBDSTTC和HBDS在训练集和测试集上的表现对比。由于本文旨在实现类人行为决策,因此正确的行为决策定义为:在自然驾驶数据中驾驶人实际的行为切换点前后3 s的时间范围内,策略能够输出与驾驶人相同的行为决策。为进一步衡量策略在类人决策上的表现,定义行为决策时间误差,即策略输出正确行为决策的时间点与驾驶人实际行为切换点之间时间差的绝对值,该值越小表明策略的类人性越强。
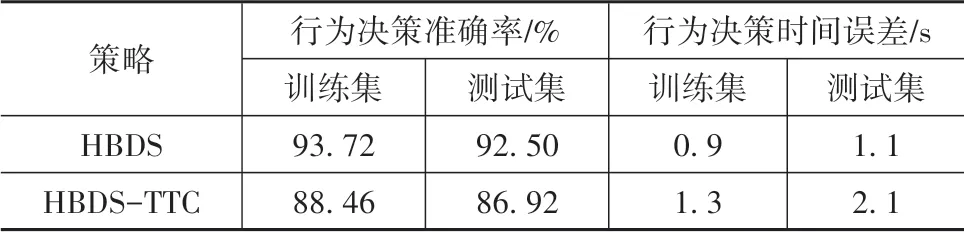
表4 有无各向异性行车风险场策略表现对比
由表4可知,HBDS-TTC的类人性低于HBDS,说明所建立的各向异性行车风险场能够更好地表征驾驶人对风险的认知,从而得到更加合理行车风险奖励函数和行车侵略度奖励函数。
(2)为验证基于统计学规律的预期轨迹空间压缩和基于安全约束的预期轨迹空间剪枝的有效性,设置3组对比试验,并在表5中给出了各组试验中奖励函数收敛即策略收敛所需的平均回合数对比。由表5可知,基于统计学规律的预期轨迹空间压缩能有效提升策略采样效率,显著降低策略收敛所需回合数,相比之下基于安全约束的预期轨迹空间剪枝对采样效率的提升幅度较小,其主要作用在于提升数据驱动的HBDS安全性。
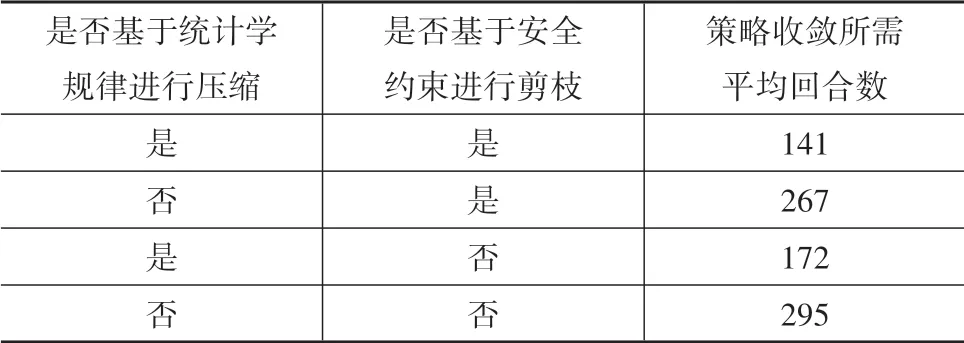
表5 策略收敛回合数对比
(3)本文在HBDS的离线训练过程中引入了交通车轨迹预测,即预测自车按照某一预期轨迹行驶过程中周围交通车将如何运动,从而建立更加真实的策略训练环境。为验证引入交通车轨迹预测的有效性,建立无交通车轨迹预测的对比策略(HBDSwithout prediction,HBDS-WP)。在HBDS-WP的训练过程中,所有交通车均按照数据集中的原始轨迹行驶,而不会根据自车的不同行为做出交互响应。对比结果如表6所示。
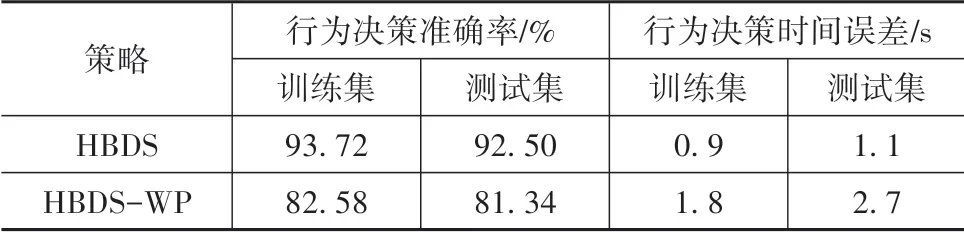
表6 有无交通车轨迹预测策略表现对比
由表6可知,没有交通车轨迹预测的HBDS-WP无法考虑自车不同行为对周围交通车的交互影响,使策略提取的类人奖励函数权重精度较差,从而导致策略类人性下降,证明了本文在HBDS中引入交通车轨迹预测的有效性。
(4)为证明HBDS相比于现有类人行为决策策略的性能提升,本文额外建立了2组策略与HBDS进行对比验证:①基于NGSIM数据集标定文献[4]中FSM的状态转移条件,构建行为决策策略;②采用与HBDS相同的MDP,以LCL、LK、LCR为动作,基于深度Q网络(deep Q network,DQN)构建行为决策策略。DQN使用与HBDS完全相同的奖励函数子项,但各奖励函数子项权重未经ME-IRL标定,各子项权重均取1。表7给出HBDS和2组对比模型在包含500位驾驶人数据的训练集和测试集上的平均表现。
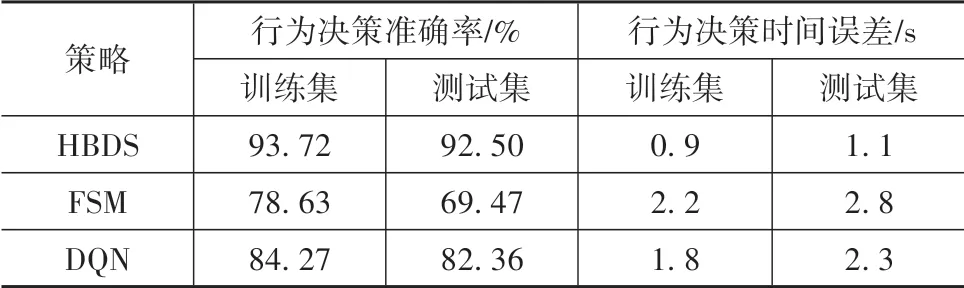
表7 HBDS与其他策略表现对比
从表7可知,HBDS具有最高的行为决策准确率和最小的行为决策时间误差。虽然经过自然驾驶数据集的标定,但完全基于先验知识和手写规则的FSM在类人决策上的表现仍不理想,且相比训练集,FSM在测试集上表现降低较为明显;使用与HBDS相同MDP的DQN行为决策准确率高于FSM,且测试集相对训练集的掉点幅度较小,也侧面证明了本文所设计的奖励函数的合理性。但由于缺少对类人奖励函数权重的离线学习,使用均一化权重的DQN表现弱于HBDS,证明了本文将驾驶行为机制引入HBDS,从自然驾驶数据中挖掘类人奖励函数权重的有效性。
5.2.2 轨迹分析
HBDS除能够输出累积奖励最高即最类人的行为决策(LCL/LK/LCR)外,还能输出该类行为对应的轨迹空间中与人类驾驶员最接近的轨迹。图9给出两个案例中HBDS概率最高的轨迹与规则化后的驾驶人轨迹对比,可以看到轨迹匹配度较高。
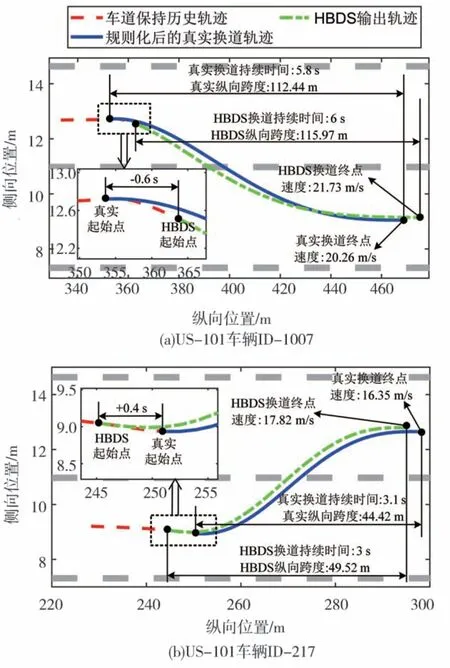
图9 HBDS概率最高轨迹与规则化处理的真实轨迹对比
由于HBDS的预期轨迹空间是基于轨迹持续时间和轨迹终点速度张开的,因此HBDS在行为决策的同时还能给出这两个决定轨迹具体形状的重要参数,对后续的运动轨迹规划具有重要意义。表8给出在测试集上,与驾驶人真实轨迹相比,HBDS输出的换道轨迹持续时间、轨迹终点速度以及轨迹纵向跨度的平均绝对误差MAE。可以看到在相同初始状态下,HBDS能给出与驾驶人十分接近的换道持续时间、轨迹终点速度和纵向跨度。而如果进一步细化表2中的取值粒度,HBDS的类人性可进一步提升,但这会降低采样效率。因此HBDS在实际应用时,应综合考量算力消耗和驾驶类人性来选定预期轨迹空间的取值粒度。

表8 概率最高轨迹与真实轨迹关键指标MAE
6 结论
面向类人驾驶这一汽车智能化技术领域的重要研究内容,对驾驶行为生成机制进行系统分析和抽象描述,提出了一种基于驾驶行为生成机制的类人行为决策策略HBDS。HBDS具有匹配驾驶行为生成机制的策略架构以及匹配驾驶人认知特性的奖励函数,并通过统计学规律与安全约束对离散化的策略采样空间进行压缩和剪枝,避免了高维连续空间的维数灾难以及预期轨迹与驾驶人实际轨迹相差较大的问题。交通车轨迹预测的引入进一步保证了HBDS的离线训练效果和在线使用性能表现。HBDS通过ME-IRL学习类人的奖励函数权重,基于BNM建立行为概率与其累积奖励的映射关系。在自然驾驶数据集上的验证结果表明,HBDS能够较好地匹配驾驶人的个性化认知特性和行为特征,并实现类人行为决策。作为一种特征驱动的类人行为决策策略,HBDS为智能汽车类人驾驶向机理层下探和策略白盒化提供了新思路。但目前HBDS中未考虑奖励函数的动态时变,且高速公路的应用场景相对简单。在后续研究中,将在环岛和十字路口等更为复杂的工况下,进一步探索驾驶人认知特性和行为特征随交通环境、自身状态等因素的变化,构建时变型奖励函数及其自适应匹配体系,并与类人运动规划结合形成完整的特征驱动下智能汽车决策规划策略。
