纯电动汽车电驱动系统耦合动力学研究*

刘长钊，张 铁，宋 健，尹显颂，葛帅帅，2

（1.重庆大学，机械传动国家重点实验室，重庆 400044；2.重庆理工大学车辆工程学院，重庆 400054）

前言

近年来纯电动汽车成为研究的热点，而电驱动系统作为纯电动汽车的心脏，取消了联轴器和离合器，这不仅提高了系统的传动效率，还降低了整车体积和质量。但是，电机转子和齿轮系统直接耦合的方式容易造成齿轮啮合状态恶化，产生较大的振动和噪声。同时，电驱动系统内存在多源复合激励，如电磁转矩、时变啮合刚度、齿轮误差和箱体柔性等，且电机电磁特性与齿轮内激励特性存在交互作用，使得电驱动系统的动态特性更加复杂。因此，研究电驱动系统振动产生机理，特别是研究多源复合激励对电驱动系统动态特性的影响，对提高系统集成设计能力和优化能力具有重要意义。

针对电动汽车齿轮系统，Setiawan等［1］通过建立变速器的数学模型，重点分析了变速器的瞬态动力学响应。Hou等［2］建立了考虑传动系统柔性的动力学模型，分析了齿轮腹板和轮缘厚度对齿轮动态啮合力矩的影响。Dabrowski等［3］建立了行星齿轮箱刚柔耦合模型，研究了传递误差和齿轮制造误差对箱体振动的影响。纪显奇［4］建立了行星齿轮传动系统模型，研究了齿轮传递误差对传动系统振动响应的影响。段元旺［5］利用有限元法研究了两挡变速器的动力学特性。陶庆等［6］研究了行星齿轮传动系统在不同齿圈厚度下的固有频率。以上学者主要研究齿轮传动系统的固有特性和动态特性，但对机电耦合的研究不足。

针对电机模型，邱家俊等［7］研究了电机启动时转子轴在交变电磁力矩作用下的振动特性。Park等［8］利用传递矩阵法建立了电机转子系统动力学模型，研究结果表明机电耦合系统的振动响应幅值比纯机械系统的响应幅值大。Mandic等［9］通过主动控制减小了电机转子系统的扭转振动。Xiang等［10］研究了在不平衡磁拉力作用下永磁同步电机转子的稳定性和频响特性。陈星［11］建立了车用永磁同步电机转子轴系动力学模型，研究了电磁参数和结构参数对转子振动的影响规律。左曙光等［12］建立了考虑定子各向异性的永磁同步电机模型，通过优化定子轭的厚度来降低电机振动的峰值。以上研究建立了电机转子振动机电耦合模型，但对于一体化电驱动系统，电机电磁转矩通过转子传递到齿轮传动系统，电机和齿轮系统的耦合作用比单转子的耦合问题更加复杂，因此需要建立一个计入齿轮传动系统的机电耦合动力学模型。

针对电动汽车电驱动系统机电耦合特性，于蓬等［13］建立了考虑结构柔性的电动汽车传动系统机电耦合动力学模型，研究了控制策略对多物理场耦合作用下系统动态特性的影响。Hu等［14］建立了电机和传动系统耦合的瞬态动力学模型，利用一种主动阻尼控制策略抑制了传动系的扭转振动。Fan等［15］建立了双电机耦合驱动系统（DCDS）的动力学模型，研究了齿轮啮合刚度和电磁激励对系统动态特性的影响。Yi等［16］建立了包含电机的多级齿轮传动系统动力学模型，研究了电磁扭转刚度对系统固有特性的影响。葛帅帅等［17］建立了电动汽车电驱动系统机电耦合动力学模型，分析了典型工况下齿轮系统扭转特性和定子电流的动态响应特性，结果表明电机和齿轮系统之间存在强耦合效应。Chen等［18］建立了开关磁阻—行星齿轮电驱动系统模型，研究了万向节对系统特性的影响，结果表明引入万向节会增强电机与行星轮系统之间的耦合效应。以上学者的机电耦合动力学特性的研究考虑了齿轮传动系统和电机系统的内激励，但齿轮系统与电机系统的动力学模型进行了相应简化，忽略了轴段、壳体柔性以及电机电磁径向力的影响。

纯电动汽车电驱动系统是高度集成的机电系统，因此本文提出了一种适用于变速等非稳态工况且综合考虑电磁激励、齿轮内激励以及一体化系统结构特性的机电耦合动力学模型，研究了稳态和加速工况下多源激励对电驱动系统动态特性的影响。

1 电驱动系统耦合动力学建模

图1为纯电动汽车电驱动系统结构简图，主要分为永磁同步电机、齿轮传动系统和箱体3部分。

图1 纯电动汽车电驱动系统结构

1.1 永磁同步电机动力学建模

本文采用有限元法建立永磁同步电机模型，首先利用有限元软件导出电机的径向和切向磁通密度，然后根据Maxwell应力张量理论，得到径向和切向电磁力密度p（rθ，t）、p（tθ，t）：

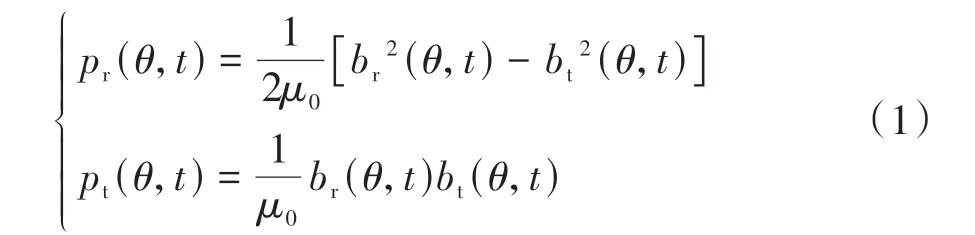
式中：μ0为空气磁导率，为4π×10-7H/m；br、bt分别为径向和切向气隙磁密。图2为电机的径向和切向电磁力密度时空分布图，将得到的电磁力密度在定子齿所在的区间上积分，即可得定子齿所受的集中电磁力。

图2 电机电磁力密度

图3为第n个定子齿的受力分析图，为便于与箱体耦合，将集中电磁力转换到直角坐标系中，坐标变换矩阵如式（2）所示。其中：Frn、Ftn分别为第n个定子齿所受径向和切向电磁力；Fxn、Fyn、Fzn分别为直角坐标系下x、y、z方向上的力。

图3 电机定子齿受力分析

1.2 旋转构件和箱体有限元缩聚模型

1.2.1 模态缩聚理论

系统的运动方程由式（3）表示，其中：M、Cd、K分别为系统质量、阻尼、刚度矩阵；u为位移矢量；F为载荷矢量。

式（3）可在模态坐标下解耦，如式（4）所示。其中：yj为系统第j阶模态坐标；ξj、ωj分别为第j阶模态阻尼比和模态频率；Φj为第j阶振型矢量；ndof为总自由度数。

高阶模态的影响一般是有限的，为简化计算，可求解式（4）的前n个方程，则得到状态方程：

其中：

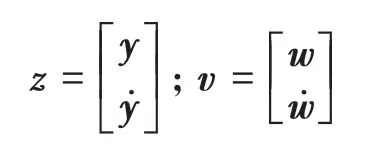
式中：y是模态坐标向量；w是系统的集中节点位移列阵分别是状态空间矩阵。

1.2.2 有限元缩聚模型

图4为电机转子轴集中节点划分示意图。其中：转子缩聚节点用于输入电磁转矩；轴颈缩聚节点1、2用于耦合轴承单元；齿轮缩聚节点用于建立啮合单元。

图4 电机转子轴缩聚模型主节点划分

中间轴和差速器壳体集中节点划分如图5所示，集中节点分别为轴颈和各齿轮的理论中心。

箱体主要集中节点划分如图6所示，箱体通过集中节点和系统其它部件进行耦合。

图6 箱体缩聚模型主节点划分

1.3 平行轴斜齿轮动力学建模

图7为主动轮右旋且绕z轴逆时针旋转的斜齿轮副6自由度动力学模型。齿轮副沿啮合线方向的总变形δ为

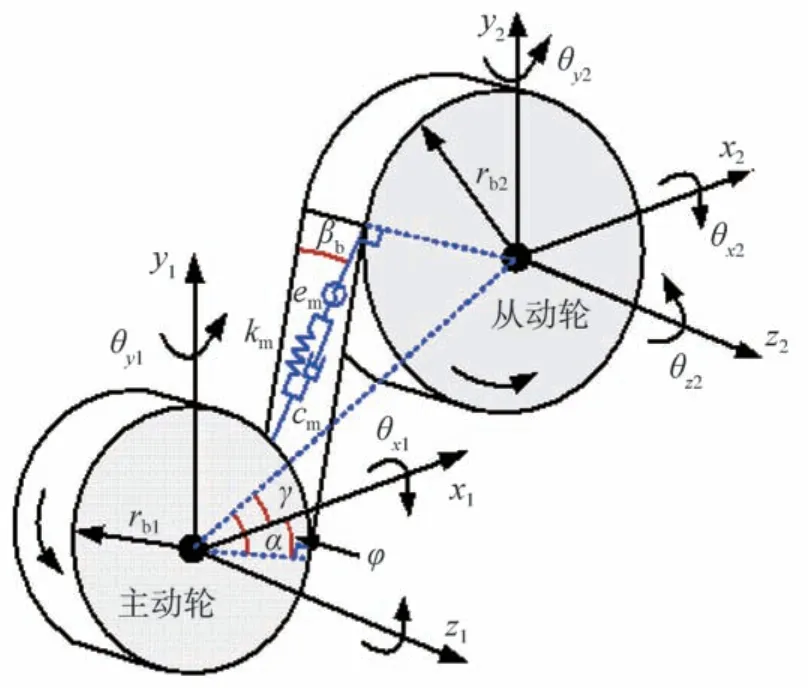
图7 斜齿轮啮合模型

式中：xi、yi、zi分别为齿轮（ii=1、2）在x、y、z方向上的平移位移；θxi、θyi、θzi分别为齿轮（ii=1、2）在x、y、z方向上的角位移；φ为主动轮上垂直于啮合面的半径与x正方向的夹角；rb1、rb2分别为主、从动轮的基圆半径；γ为啮合线与x轴正向的夹角；βb为基圆螺旋角；em为齿轮误差；km为啮合刚度。

本文将齿轮副的时变啮合刚度表达为齿轮角位移的函数，并使之用于变速过程。同时考虑齿轮加工过程中的误差，用伪随机数来模拟齿轮误差激励，图8和图9分别为一级齿轮副的时变啮合刚度和齿轮误差激励。

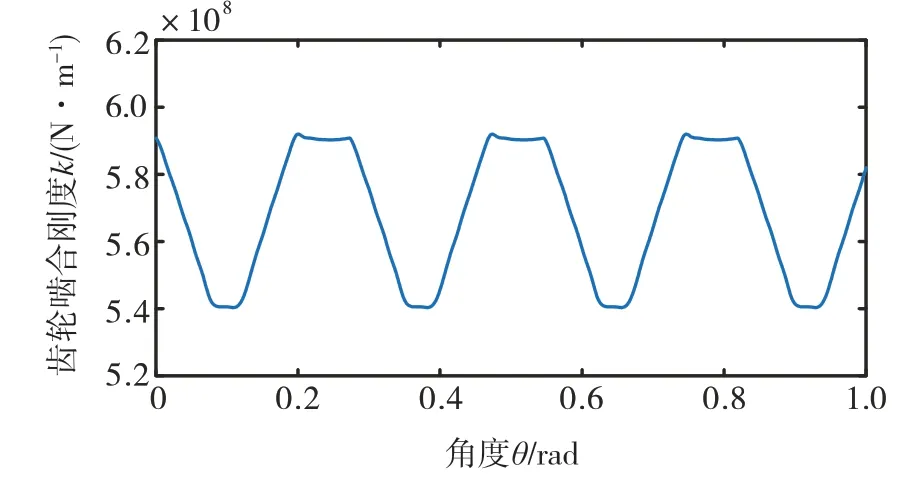
图8 一级齿轮副时变啮合刚度

图9 一级齿轮副齿轮误差

考虑齿侧间隙后齿轮副沿啮合线方向的总变形如式（7）所示。

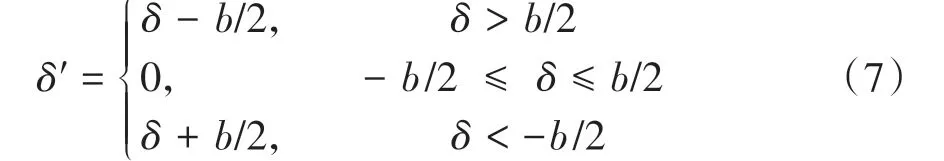
式中：δ、δ′分别为考虑齿侧间隙前后齿轮副沿啮合线方向的总变形；b为齿侧间隙。

1.4 差速器动力学建模

直齿锥齿轮副的啮合模型如图10所示。其中：rbj是直齿锥齿轮j的啮合点半径；δb为锥齿轮节锥角；αn为法面压力角；k、c、e分别为啮合刚度、啮合阻尼、综合齿轮误差。

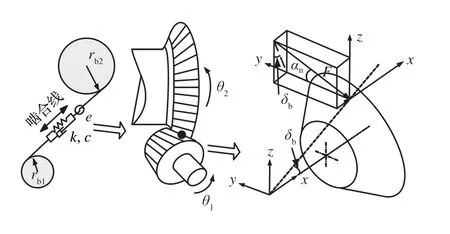
图10 直齿锥齿轮啮合模型及受力分析

则直齿锥齿轮副沿啮合线的相对总变形为

差速器动力学模型如图11所示。图中建立了3个坐标系：（1）静止坐标系OXYZ；（2）随差速器壳体转动的动坐标系oxyz；（3）原点位于行星齿轮中心的动坐标系opnxpnypnzp（nn=1，2，…，N，N是行星齿轮个数）。其中：符号x、y、z、θ分别为x、y、z方向上的平移位移和角位移；下标p、b、c分别代表行星齿轮、半轴齿轮、差速器壳体，以上构件各方向上的位移都是在动坐标oxyz中测量的；θc为差速器壳体在静止坐标系OXYZ中测得的转角；φn是第n个行星齿轮的位置角，φn=2π（n-1）/N；Tm为作用在第m个半轴齿轮上的阻力矩。

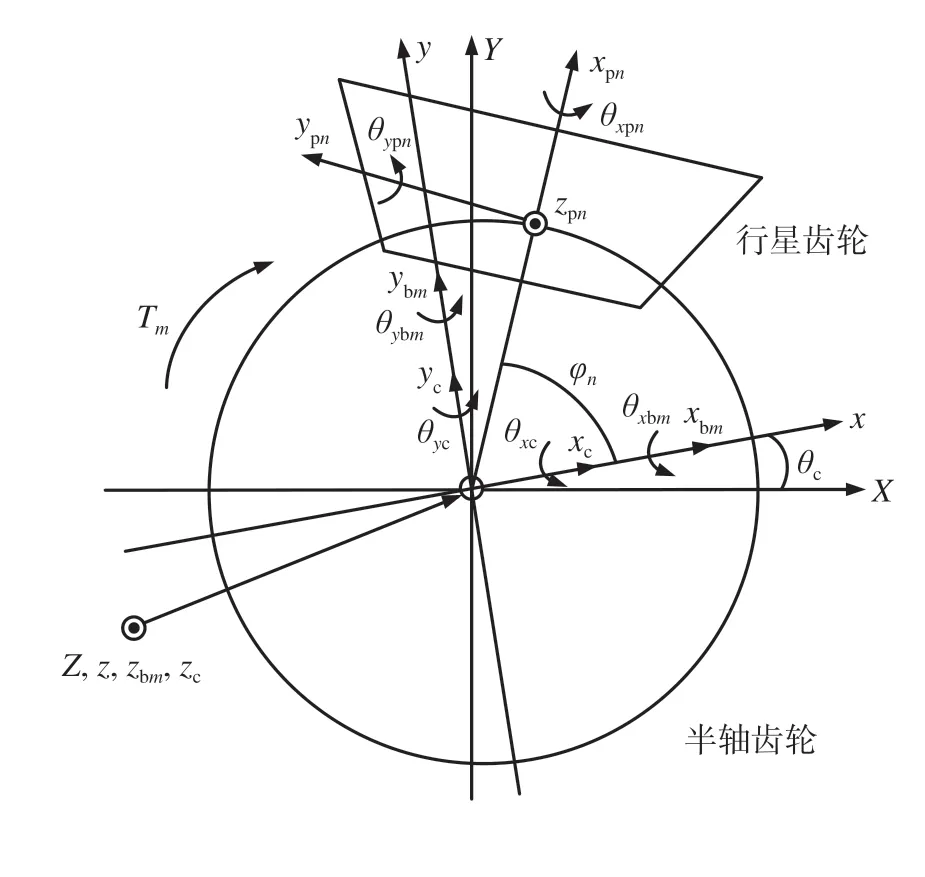
图11 差速器动力学模型

利用非惯性坐标系的牛顿定律来获得第m个（m=1，2）半轴齿轮的运动微分方程，如式（9）所示。其中：mb、Jxb、Jyb和Jzb分别是半轴齿轮的质量和绕自身x、y、z轴的转动惯量；FPB（x，y，z）bnm和MPB（x，y，z）bnm分别为行星齿轮作用在半轴齿轮上的力和力矩；下标n（n=1，2）、m（m=1，2）分别代表第n个行星齿轮和第m个半轴齿轮；kxb、kyb、kzb、ktxb和ktyb分别为半轴齿轮在x、y、z、θxb、θyb向的接触刚度；cxb、cyb、czb、ctxb和ctyb分别为半轴齿轮在x、y、z、θxb、θyb向的接触阻尼；δbmcx、δbmcy、δbmcz、θδbmcx和θδbmcy分别表示第m个半轴齿轮与差速器壳体在各个方向的相对位移。

第n个行星齿轮的运动微分方程如式（10）所示，式中各符号含义与式（9）中类似。

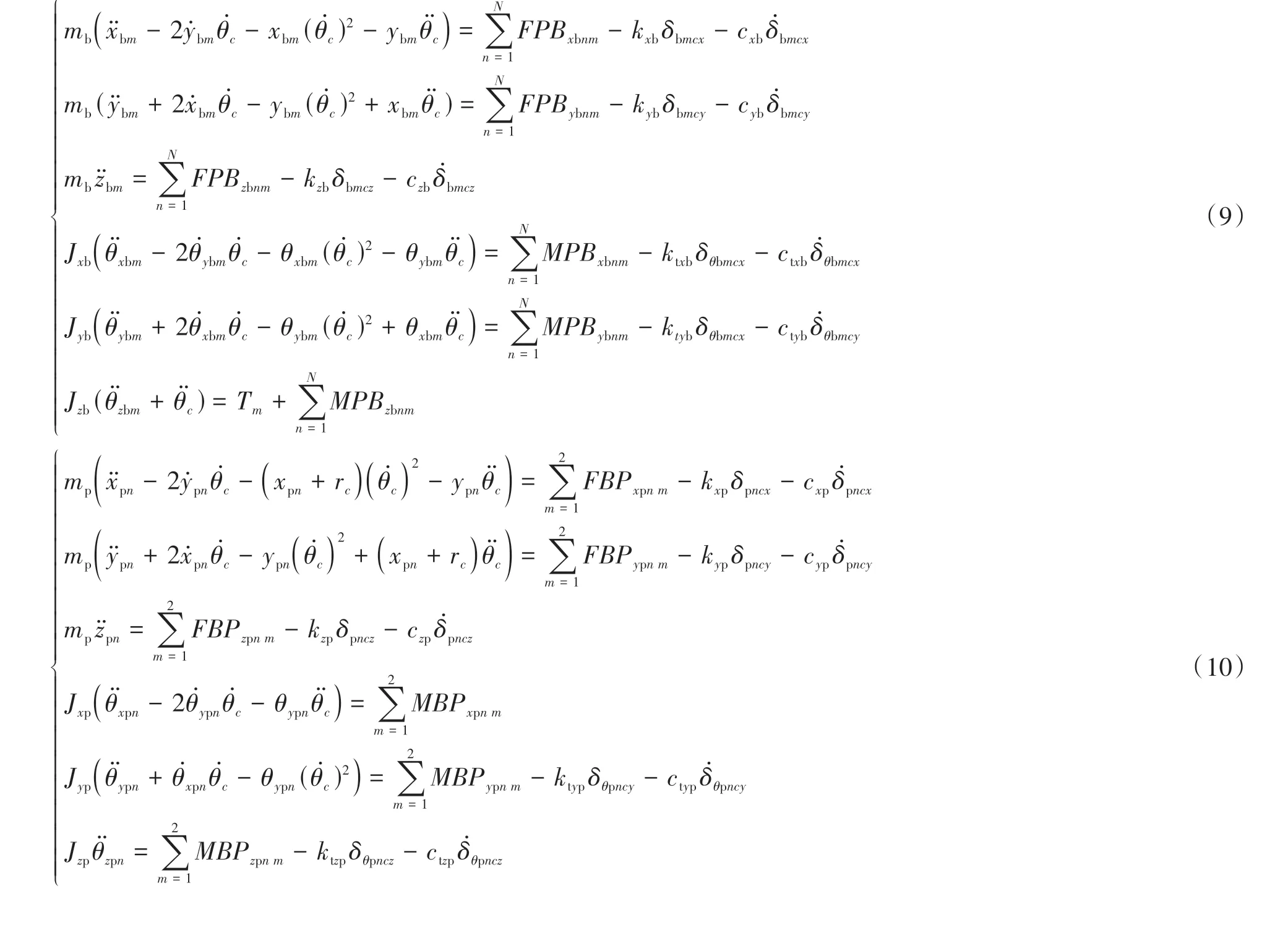
1.5 电驱动系统机电耦合模型

电驱动系统主要参数如表1所示。根据永磁同步电机模型和传动系统动力学模型，建立电驱动系统机电耦合模型，如图12所示。

图12 耦合系统动力学建模流程图

表1 电驱动系统主要参数

系统各构件之间以相互作用力和位移关系进行耦合。电机的电磁转矩作为驱动力矩作用在转子轴上，径向和切向电磁力作用在与箱体耦合的定子齿上，负载力矩作用在差速器上；根据齿轮节点的位移和速度计算齿轮副啮合力，且通过转子轴和中间轴上的齿轮传递啮合力；利用旋转构件和箱体在轴承节点上的相对位移和相对速度来计算轴承的支反力，然后所有轴系通过轴承支反力与箱体耦合。

2 稳态工况下系统动态特性研究

2.1 有限元验证缩聚模型正确性

为了从动力学角度验证箱体缩聚模型的正确性，在缩聚模型和有限元软件中分别对箱体轴承集中节点2（位置见图6）在X、Y、Z方向施加5 000 N的集中力。有限元软件中计算得到集中节点2的变形位移其值为687.96 μm。缩聚模型中集中节点2的动态位移如图13所示，两者结果的相对误差为4.38%，说明缩聚模型与有限元模型的计算结果吻合较好。

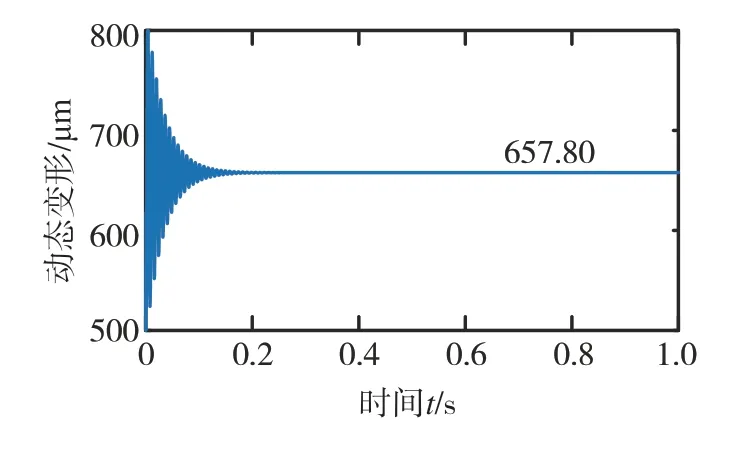
图13 轴承集中节点2动态位移

在有限元软件中设转子轴转速为1 000 rad/s，提取转子轴外表面网格节点（节点序号为35818）在径向的变形位移，其值为2.51 μm，图14为该转子网格节点位置示意图。在缩聚模型中以相同转速对转子轴进行动力学仿真，该网格节点在径向的动态位移如图15所示。该节点动态位移收敛到2.48 μm，与有限元模型的绝对误差为0.03 μm，相对误差为1.2%，结果吻合较好，验证了所建模型的正确性。

图14 转子网格节点选取

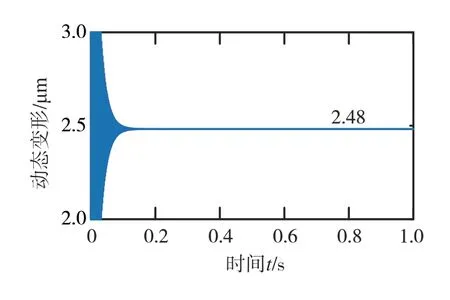
图15 网格节点径向动态位移

2.2 内部激励对系统动态特性的影响

2.2.1 电机转矩波动的影响

（1）齿轮动态啮合力矩

图16为电机输出转矩频谱图。电机转矩的频率成分主要是电机基频fmb=2000 Hz及其倍频。

图16 电机转矩频谱

图17为电机转矩波动对一级齿轮副动态啮合力矩影响的时域图及频谱图。由图可知，恒定电机转矩时齿轮副动态啮合力矩波动范围较小，在考虑电机转矩波动后，齿轮副动态啮合力矩均值不变，但波动的幅值明显增大；频谱图上出现了电机转矩的频率，主要成分为fmb和2fmb，且2fmb对应的幅值大于齿轮副啮合频率的幅值，这表明电机转矩波动通过转子轴传递到了齿轮系统上，并且对齿轮动态啮合力矩的影响较大。

图17 一级齿轮副动态啮合力矩时域及频谱图

图18为二级齿轮副动态啮合力矩时域图及频谱图。由图18（a）可知：电机转矩波动对二级齿轮副动态啮合力矩有影响，但影响较小；频谱图上，二级齿轮副中电机转矩频率与啮合频率幅值的差值显著减小，但仍然出现了电机电磁频率成分2fmb。这是因为在啮合阻尼和结构阻尼的作用下，同时受到传递路径的影响，距离电机较近的构件受到电磁转矩波动的影响明显，较远的构件所受到的影响较小。

图18 二级齿轮副动态啮合力矩时域及频谱图

（2）轴承动态支反力

图19为电机转矩波动对轴承2（位置为图6中轴承节点2）动态支反力影响的时域图及频谱图。由此可知，两条曲线基本重合，主要频率成分为电机转频fr1和齿轮啮合频率fm1，而电机转矩频率fmb幅值很小，即电机转矩波动对轴承动态支反力的影响很小。

图19 轴承2动态支反力时域及频谱图

2.2.2 齿轮误差的影响

（1）齿轮动态啮合力矩

图20为齿轮误差对一级齿轮副动态啮合力矩影响的时域图。由此可知，齿轮动态啮合力矩在考虑齿轮误差后波动幅值显著增加，远大于电机转矩波动对动态啮合力矩的影响。

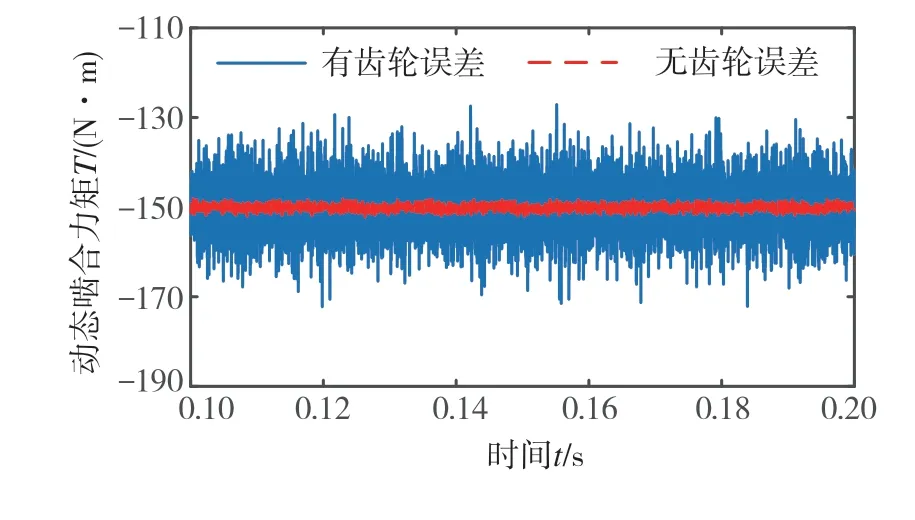
图20 一级齿轮副动态啮合力矩

图21为一级齿轮副齿轮误差频谱图，图22为一级齿轮副动态啮合力矩频谱图。由图21可知，频谱图上出现了连续的区域，这是因为本文以伪随机数模拟齿轮误差，频率成分复杂。结合图21和图22，可以发现在高频区域中的频率成分主要来自于齿轮误差。这说明一级齿轮副动态啮合力矩的幅值增大，齿轮误差激励起到了关键性的影响。

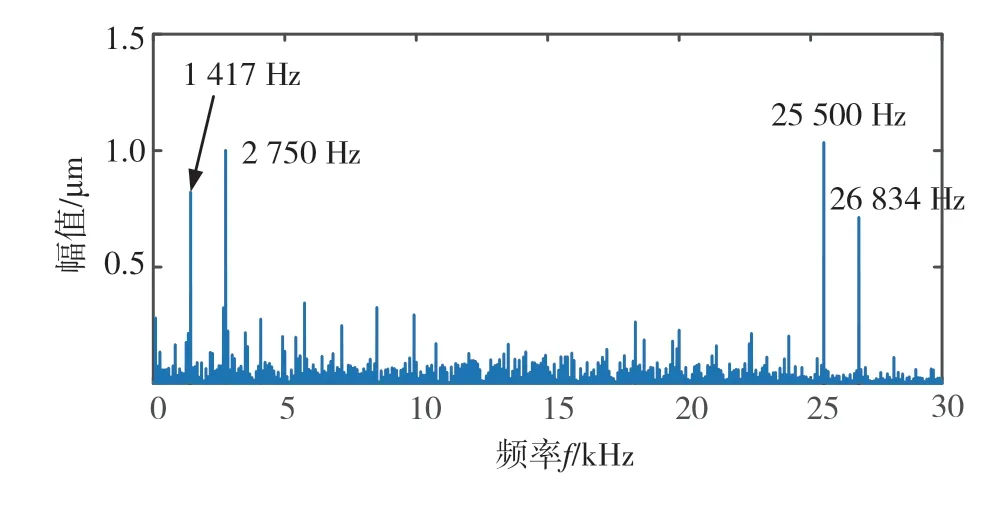
图21 一级齿轮副齿轮误差频谱图

图22 一级齿轮副动态啮合力矩频谱图

（2）轴承动态支反力

图23和图24分别为齿轮误差对轴承1、2（位置见图6）动态支反力影响的时域图及频谱图。从图23中可以看出：考虑齿轮误差后轴承动态支反力波动明显增加；频谱出现了幅值较大的成分1 417 Hz，该频率可以在图21中找到，这表明了齿轮误差激励作用在齿轮副上，然后通过传动轴传递到了轴承上。

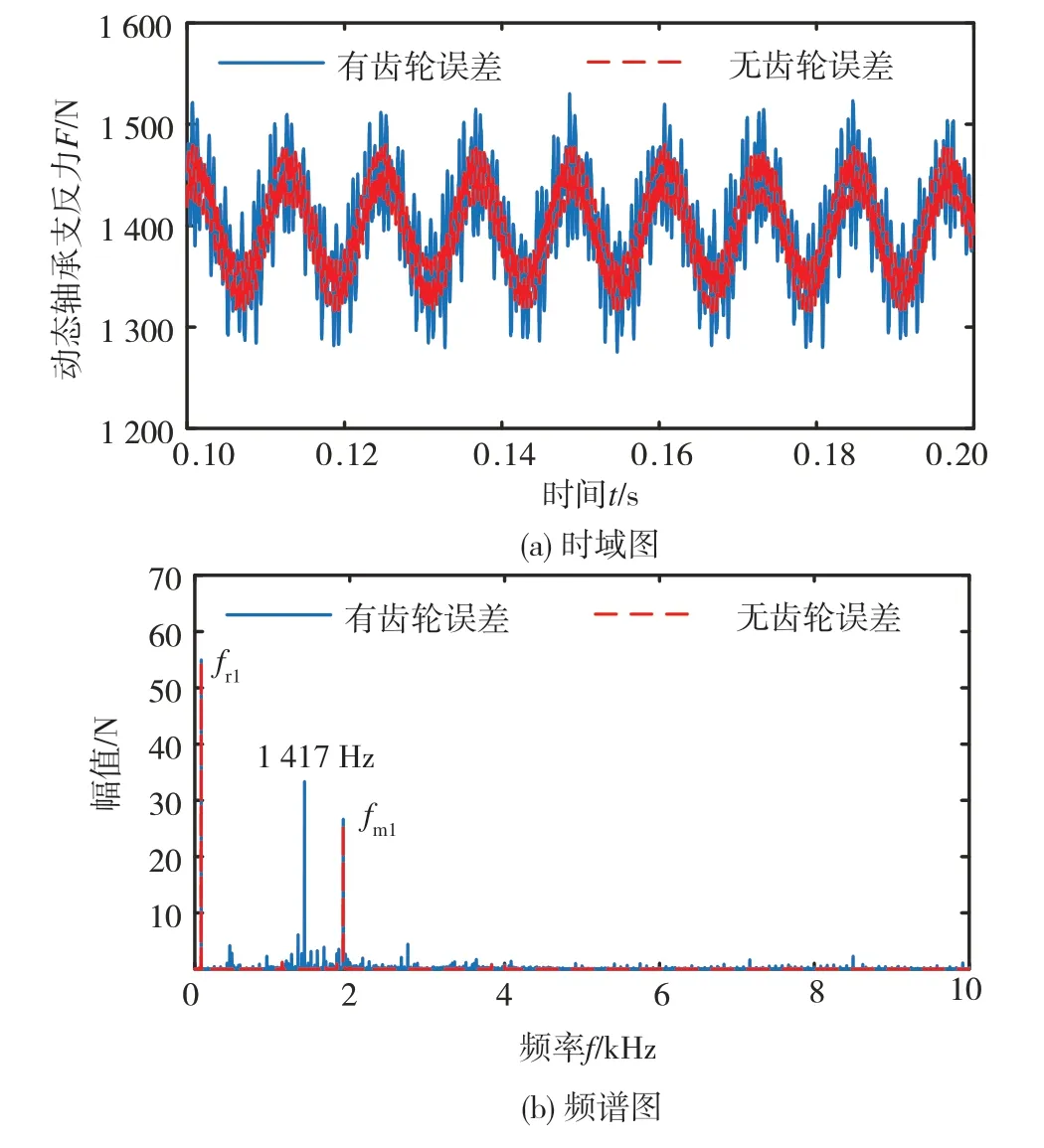
图23 轴承1动态支反力时域及其频谱图

对比图23和图24，发现轴承2的动态支反力频谱范围更宽，频率成分更复杂，这是因为轴承2的安装位置离齿轮副更近，由齿轮啮合产生的激励力传递到轴承2处，对轴承2的影响更加明显。由图24可知，轴承2的动态支反力频率范围主要集中在0～15 000 Hz，引入齿轮误差后产生的高频成分如25 500 Hz和26 834 Hz的幅值较小，这表明高频成分对轴承支反力的影响不大。

图24 轴承2动态支反力时域及其频谱图

2.2.3 箱体对系统动态特性的影响

（1）齿轮动态啮合力矩

图25为耦合箱体前后一级齿轮副动态啮合力矩时域图和频谱图。可以看出耦合箱体前后齿轮副动态啮合力矩的均值和振幅基本不变，且频率成分变化也较小，说明耦合箱体对齿轮动态啮合力矩的影响不大。这是因为齿轮副动态啮合力矩主要受外载荷、齿轮啮合刚度和齿轮误差等因素的影响，而耦合箱体前后外载荷、啮合刚度和齿轮误差基本不变，故耦合箱体后齿轮动态啮合力矩的变化不大。

图25 一级齿轮副动态啮合力矩时域及频谱图

（2）轴承动态支反力

图26为耦合箱体前后轴承1、2的动态支反力时域图。可以看出耦合箱体后轴承1的动态支反力均值变小，而轴承2的动态支反力均值则略微增大，这是因为在不同轴承位置处薄壁箱体的壁厚及结构设计不同，导致等效支撑刚度也不同。因此耦合箱体后集中节点处的动态位移将发生变化，导致轴承力随之而改变。耦合箱体后，轴承1的等效支撑刚度变化更大，故其动态支反力变化也更大。

图26 轴承1和轴承2动态支反力

3 加速工况下系统动态特性研究

当路面拥堵时，汽车频繁起停和加速，导致驱动电机长时间运行在变速工况下。在电驱动系统调速过程中，当内外部激励频率跨越系统固有频率时，系统可能发生共振，这会影响到汽车行驶过程的可靠性和安全性。因此本节分析了加速过程下系统的共振情况。本节将一体化电驱动系统分为耦合系统（耦合箱体）和齿轮传动系统（不耦合箱体），并对两者展开研究。

3.1 加速工况下齿轮传动系统共振分析

3.1.1 齿轮传动系统特征值计算

特征值反映了系统的稳定性，因此在进行共振分析之前，需要先计算系统的特征值。特征值的实部表示系统衰减系数，虚部对应固有频率。对于具有一般阻尼的系统，其特征值可能为实数，也可能是具有负实部的复数，复特征值将成对存在，且会出现虚部为0的特征值，因此表2只给出虚部绝对值大于零的部分阶数特征值。

表2 不耦合箱体下系统特征值

分析可得：（1）特征值实部全为负实数，表明系统趋于稳定；（2）在某些相邻的阶数，如32阶和33阶、38阶和39阶等特征值十分接近，这是因为系统中轴承支撑刚度在水平和竖直方向的数值相同，均等于径向支撑刚度。

3.1.2 齿轮传动系统共振分析

为分析系统的共振，让驱动电机的转速从0匀速上升到10 000 r/min，图27为加速过程中电机转速及转矩激励时域图。为使图片清晰，转矩激励时域图只给出了仿真前0.2 s的数据。

图27 电机转速及转矩激励

（1）不考虑齿轮误差

图28为系统在不考虑齿轮误差时一级齿轮副动态啮合力矩时域图，为了消除仿真初始的瞬态波动，仿真前0.3 s的数据未采用。可以看出，在0.44、0.88、1.70和3.70 s附近，动态啮合力矩的振幅明显增大，表明这几个时刻所对应的电机转速为系统的共振转速。

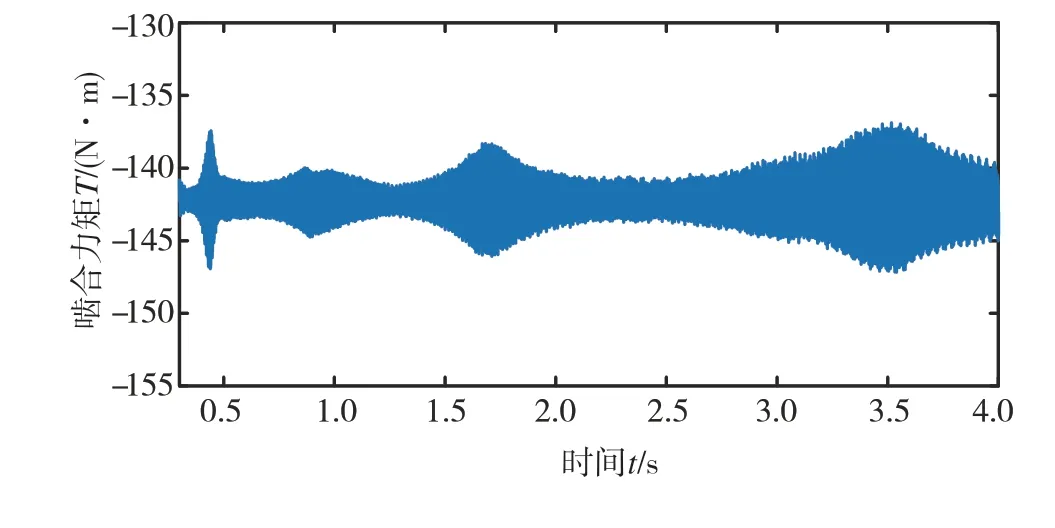
图28 一级齿轮副动态啮合力矩时域图

采用短时傅里叶变换（STFT）获得如图29所示的动态啮合力矩时频图，与横坐标平行的直线代表系统固有频率，红色斜线代表激励频率。

图29 一级齿轮副动态啮合力矩时频图

可以看到，导致系统共振的主要激励频率成分为电机转矩频率fmb、齿轮副啮合频率fm1和fm2。

（2）考虑齿轮误差

图30为加速过程中考虑齿轮误差时一级齿轮副动态啮合力矩时域图。可以看出，考虑齿轮误差后齿轮副动态啮合力矩均值不变，但是波动幅值明显增大，这与稳态工况下的结论类似。同时，共振峰难以从时域图上识别，必须从频域分析。

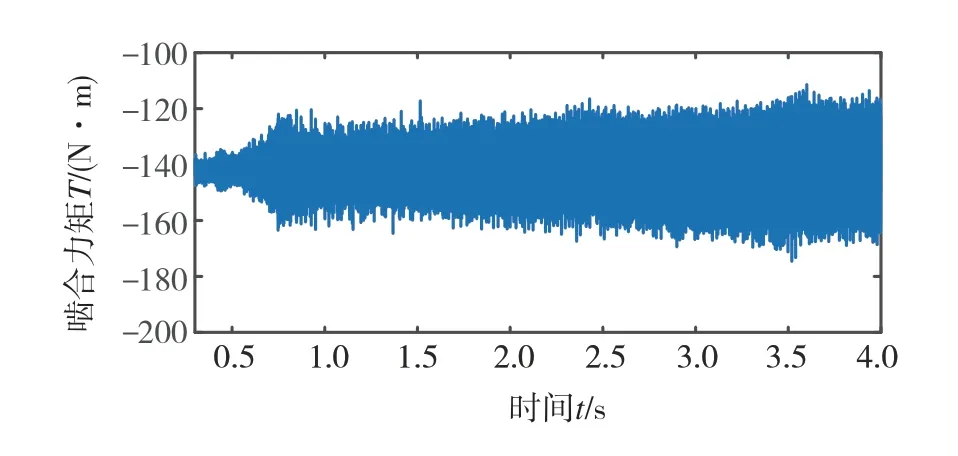
图30 一级齿轮副动态啮合力矩时域图

图31为加速过程中考虑齿轮误差时一级齿轮副动态啮合力矩时频图。可以看出导致系统发生共振的激励频率同样是fmb、fm1和fm2，但还出现一些高频成分，如3fm1、11fm2和16fm2。

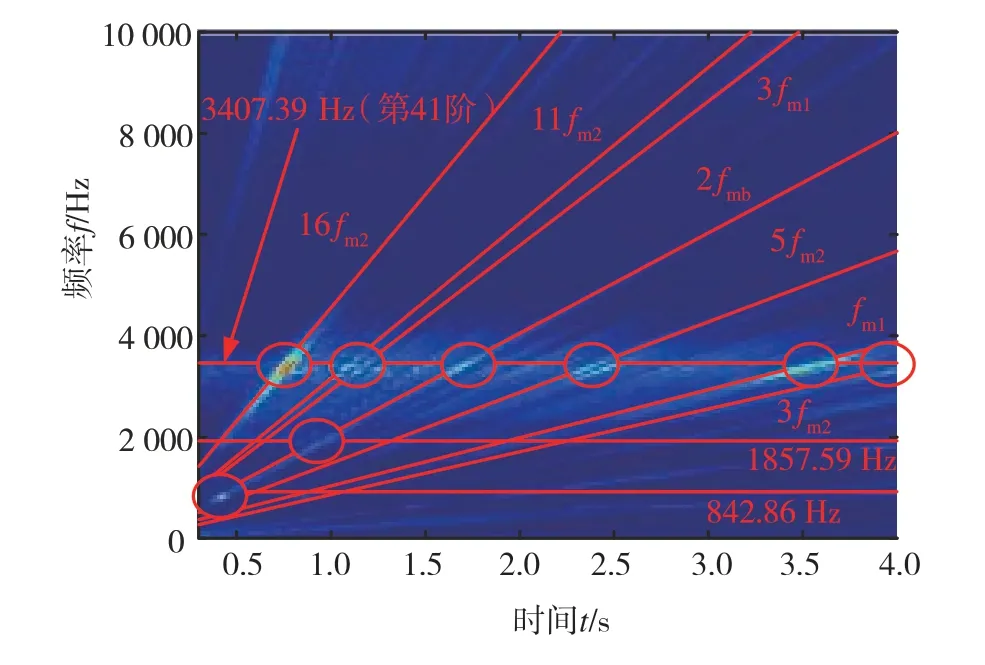
图31 一级齿轮副动态啮合力矩时频图

齿轮误差对系统共振影响的结果如表3所示，本文只给出了最危险的3个电机转速及其对应的共振频率。分析可知，考虑齿轮误差后时频图的频率成分更加复杂，出现一些由齿轮啮合频率的高倍频如3fm1、11fm2和16fm2引起的共振，且主要共振转速也发生改变。这是因为齿轮误差的频率成分复杂，频率分布范围广，更容易激发系统共振。从表3还可以看出第41阶固有频率3 407.39 Hz比较容易被激发，应重点关注。

表3 齿轮误差对系统共振影响

3.2 加速工况下耦合系统共振分析

3.2.1 耦合系统特征值计算

图32为耦合箱体前后系统前80阶固有频率对比，可以看出耦合箱体后系统固有频率明显降低，这是因为耦合箱体后系统的柔性增加。

图32 固有频率对比

表4为耦合箱体下，虚部绝对值大于零的部分阶数特征值。

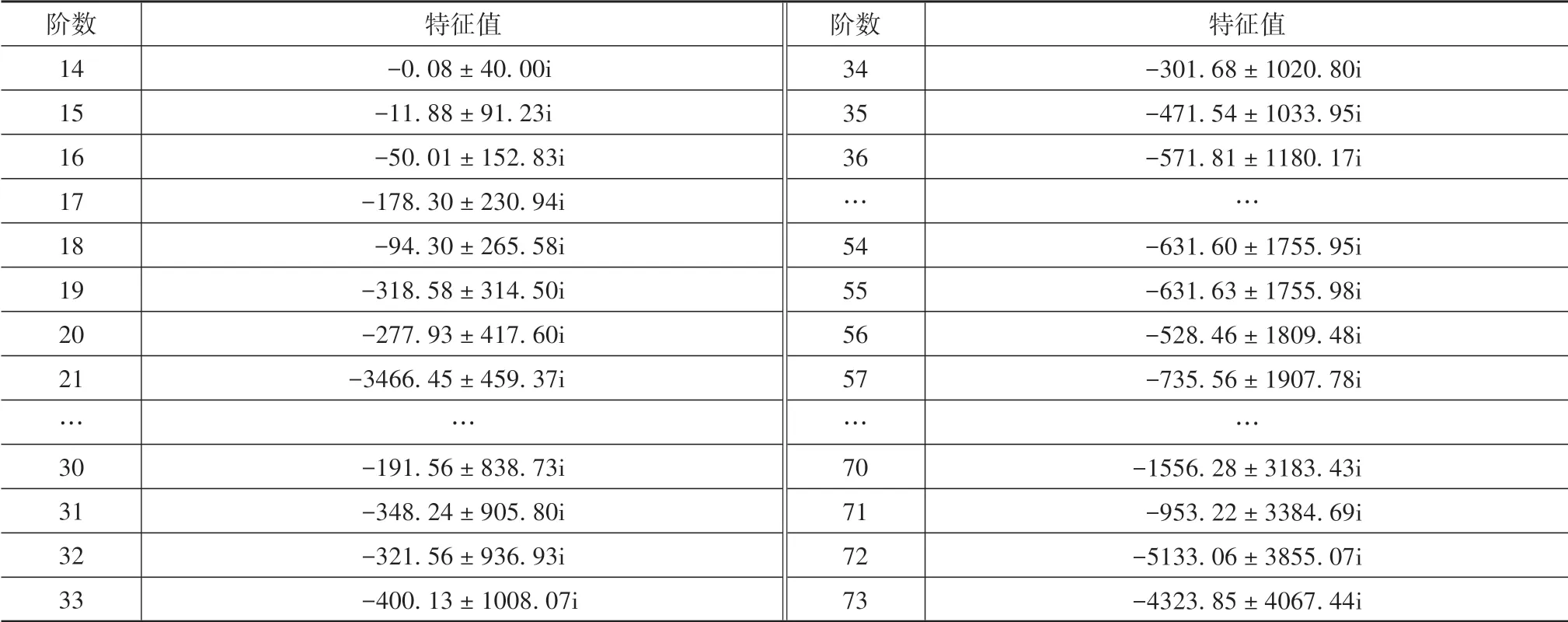
表4 耦合箱体下系统特征值

3.2.2 耦合系统共振分析

图33为耦合箱体前后一级齿轮副动态啮合力矩的时域图。可以看出：耦合箱体前后前3个主共振峰幅值波动的差异不大；但耦合箱体后，动态啮合力矩在3.7 s左右波动幅值明显变大。

图33 一级齿轮副齿轮动态啮合力矩

图34为耦合箱体后一级齿轮副动态啮合力矩的时频图。可以看出，导致系统发生共振的激励频率主要为fmb、fm1和fm2，同时还出现了由电机转频fr1引起的共振。箱体对系统共振影响的结果如表5所示。

图34 一级齿轮副动态啮合力矩时频图

表5 箱体对系统共振影响

对比耦合箱体前后系统的共振转速和共振频率，发现耦合箱体后系统共振转速和共振频率都有所降低。这是因为引入箱体柔性后，系统的固有频率降低，导致共振频率和共振转速均降低。对比表2和表3发现，耦合箱体后出现了原来没有的频率成分152.83 Hz，该频率为计入箱体后的模态频率。当电机转速为9 169.80 r/min时，转频fr1激发了耦合箱体后系统的第16阶固有频率152.83 Hz，导致3.7 s左右齿轮啮合力矩波动幅值明显变大，同时该转速下fm1激发了系统第71阶固有频率，出现了2阶固有频率共同作用的共振现象，该现象将结合图35进行讨论。

下面将从轴承动态支反力的角度验证上述结论。图35为耦合箱体前后轴承2的动态支反力时域图。可以看到在3.7 s时耦合箱体后的轴承力幅值显著增大，出现了明显的共振峰，这表明耦合箱体后系统在该共振峰对应的转速附近发生了共振，主要激励频率为fr1。综上分析可得：耦合箱体后电驱动系统的共振转速和共振固有频率均降低，且容易激发与转频相关的低阶共振。

图35 轴承2动态支反力

4 结论

本文以纯电动汽车电驱动系统为对象，建立了一种适用于变速工况且考虑电磁力时空分布和系统结构柔性的一体化电驱动系统机电耦合动力学模型，分析了在稳态和加速工况下电机转矩波动、齿轮误差和箱体柔性对系统动态特性的影响规律。

（1）稳态工况下电机波动转矩、齿轮误差、柔性箱体对系统动力学特性的影响体现在：电机转矩波动会增大齿轮动态啮合力矩的幅值，对距离电机较近位置处的啮合副影响显著，较远位置处的啮合副影响较小，但电机转矩波动对轴承力的影响不明显；齿轮误差会显著增加齿轮动态啮合力矩和轴承支反力的幅值；齿轮误差的高频成分对轴承支反力的影响不大；箱体柔性对齿轮动态啮合力矩的影响较小，箱体对轴承支反力的影响显著，但不同位置处的影响效果不同。

（2）加速工况下进行了共振分析，研究了齿轮误差和箱体对系统动力学特性的影响：导致系统共振的频率主要包括电机转矩频率fmb、齿轮副啮合频率fm1和fm2，齿轮误差容易激起系统高频成分的共振，如3fm1、11fm2和16fm2；耦合箱体后电驱动系统的固有频率显著降低，并且共振转速和固有频率均降低，耦合箱体后容易激发与转频相关的低阶共振。