横向穿孔对压电换能器振动特性的影响

高晓蕾, 刘世清, 樊叶萍, 陈赵江

(浙江师范大学 物理与电子信息工程学院,浙江 金华 321004)

0 引 言

在功率超声技术领域，为满足不同的应用要求，常对功率超声换能器的结构进行穿孔、开槽等特殊设计，以实现不同的功能.文献[1]通过在夹心式压电换能器前盖板中进行轴向半穿孔方式，降低换能器的机械品质因素来展宽换能器的频带；文献[2-3]通过纵向开狭缝的方法降低超声变幅杆的纵横耦合振动以提高超声焊接的处理效率；文献[4-7]通过在换能器变幅杆上开槽或狭缝的方式实现振动模式的转换，获得纵径、纵扭、径扭或纵弯复合模式振动，并在超声精密加工、超声电机等领域获得了广泛应用.

文献[8]提出了一种新型的热管散热型大功率压电超声换能器，该换能器通过在其振动位移节面进行穿孔用以安装热超导管以实现对换能器进行散热降温的目的.该文作者仅对位移振动节面位置附近径向穿孔换能器的振动特性进行了仿真与实验研究.事实上，径向穿孔位置将对换能器共振和反共振频率、位移振幅及有效机电耦合系数等振动特性产生较大影响[9].本文基于数值仿真法，以厚电极夹心式压电换能器为研究对象[10]，研究换能器横向穿孔位置、孔数、孔形、孔径和孔深对换能器的频率、有效机电耦合系数及位移振幅等振动特性的影响，得到了一些具有工程应用价值的结果.

1 厚电极压电换能器频率方程

图1所示为半波长厚电极夹心式压电换能器，图1中:压电陶瓷组中央为厚电极，mn为振动位移节面；L1，L2，L3，L4和2R分别表示换能器后盖板、压电陶瓷片、厚电极、前盖板的厚度和外径尺寸；2组压电陶瓷堆的内径与厚电极的内径均为2r.半波长换能器可看作由2个1/4波长换能器组成.不计损耗，单个1/4波长换能器的等效电路如图2所示.A,B为开路端，代表节面位置.对于空载，即Zbl=0.Z11，Z13，Z21，Z23，Z31及Z33分别为换能器各部分机械阻抗，n为换能器的机电转换系数，C0为压电陶瓷一维截止电容；压电陶瓷的片数p=2；Z1，Z2，Z3(下文提到)分别为1/4波长换能器前盖板、压电陶瓷堆和厚电极的等效机械阻抗，各参量具体表达式及物理意义参见文献[11].

图1 半波长厚电极压电换能器结构示意图

图2 1/4波长压电换能器等效电路图

换能器输入的电阻抗为

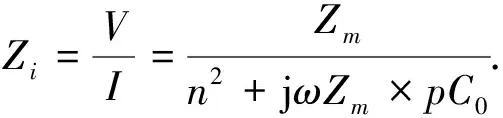
(1)

式(1)中,Zm的表达式为

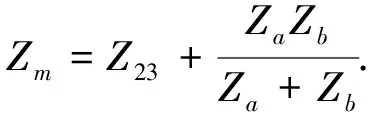
(2)

式(2)中，Za，Zb分别为：

(3)

Zb=Z21+Z31+Z33.

(4)

换能器纵向共振条件为

Im(Zi)=0.

(5)

得半波长厚电极换能器共振频率方程为

Z2(Z1tan(k1l1)-Z3cot(k3l3))+

(6)

换能器的反共振频率可由下式给出:

Im(Zi)→∞.

(7)

不计损耗，换能器的有效机电耦合系数可近似表示为

(8)

式(8)中：fr为厚电极换能器的共振频率；fa为反共振频率.

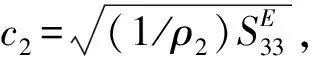
对于上述给定参数，保持厚电极换能器的总长度、位移节面位置及压电陶瓷堆的厚度不变，数值计算换能器共振频率fr、反共振频率fa和有效机电耦合系数keff随电极厚度的变化.由图3可以看出，厚电极换能器的fa与keff随L3的增加而单调递减；而共振频率fr随电极厚度的增大先下降后上升，约在40 mm处达到极小值.此时，厚电极与压电陶瓷堆的总长度为L3+4×L2，约占换能器总长度的一半.

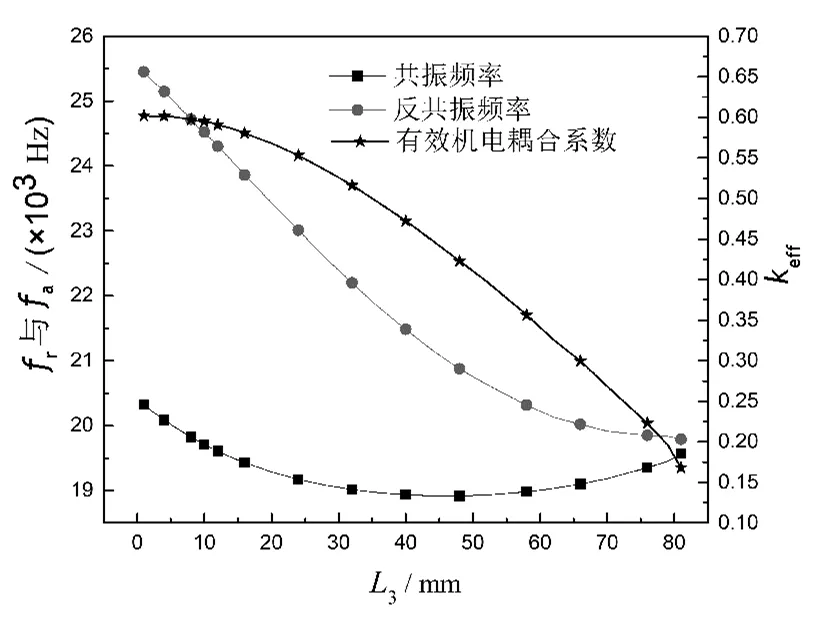
图3 fr,fa,keff 随电极厚度的变化关系

从实用上考虑，选取电极厚度为10 mm的情况进行有限元数值仿真计算.表1为未穿孔厚电极换能器基频的理论与仿真计算结果，Δ1=(|fre-fr|/fre)×100%为换能器共振频率理论值与仿真值的相对误差，fre为仿真的共振频率(fae为仿真的反共振频率).结果表明，理论与仿真吻合较好.

表1 未穿孔厚电极换能器共振频率理论值与仿真值

2 横向穿孔换能器振动特性分析

2.1 穿孔对换能器共振频率的影响

共振频率是描述换能器振动性能的重要参数之一.保持换能器几何参数不变，分别在节面处、前盖板与压电陶瓷交界面处和前盖板中部沿半径方向进行穿孔(见图4)，并得到圆形穿孔换能器的有效机电耦合系数、共振和反共振频率与穿孔参数之间的关系如图5～图7所示，其中N，d，L分别表示孔数、孔径和孔深.

(a)节面处

(b)前盖板-电极交界处

(c)前盖板中部

由图5～图7可知，在不同位置进行穿孔，换能器的共振频率、反共振频率和有效机电耦合系数皆随N，d，L的增大而减小.keff减小可能是因为随着穿孔尺寸的增加，换能器压电陶瓷堆两边的匹配块与其特性阻抗比减小，使得有效机电耦合系数降低[11].

图5 节面处穿孔fre ,fae ,keff 与孔数的关系(d=6 mm，L=5 mm)

图6 前盖板-压电陶瓷交界处穿孔fre ,fae ,keff与孔数的关系(d=6 mm，L=5 mm)

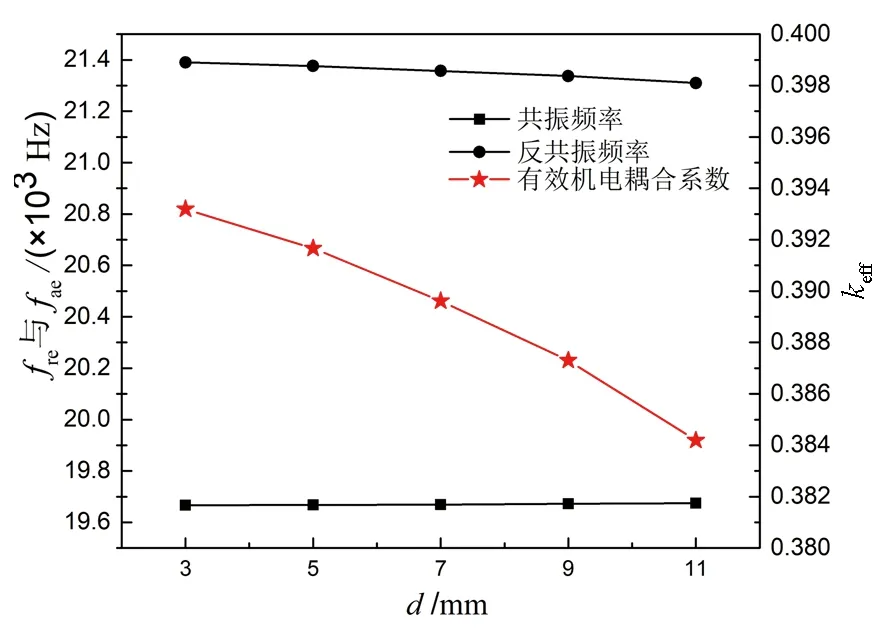
图7 前盖板中部处穿孔fre ,fae ,keff与孔径的关系(N=6个，L=5 mm)

针对方形和圆形2种孔形，以节面处穿孔为算例，改变孔数N、孔径d和孔深L，得到不同穿孔位置下换能器的共振频率与穿孔参数的依赖关系，数值仿真结果如图8～图10所示.

图8和图9为圆形穿孔换能器共振频率随N,d,L及穿孔位置变化关系.由图8可知，在前盖板中部处穿孔的换能器，其共振频率fre随L的增加而略有升高.一般说来，穿孔对换能器共振频率的影响主要表现在2个方面：一方面，穿孔会使换能器的等效刚度减小，共振频率降低；另一方面，穿孔会导致换能器的等效质量减小，共振频率升高.由于换能器工作时其节面的位移振幅最小，且此处为换能器的应力腹点，在该位置穿孔，换能器因等效刚度减小所导致的共振频率降低大于因共振质量减小所引起的频率上升，因而换能器整体共振频率随孔深及孔数增加而下降.由图9可知，fre随N，d的增大而减小；孔径d越大，fre随孔数下降得越快.

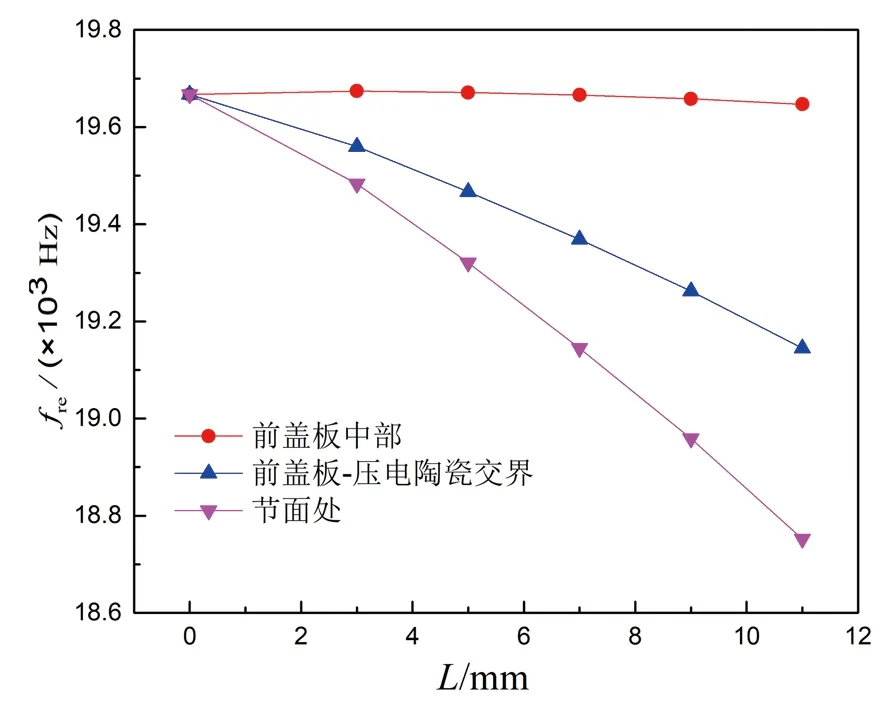
图8 fre随孔深、穿孔位置的变化关系(N=9个, d=5 mm)

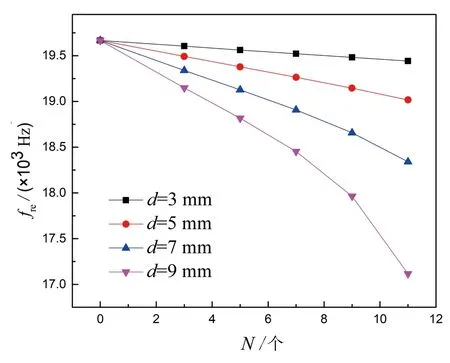
图9 fre随孔数、孔径的变化关系(L=7 mm)

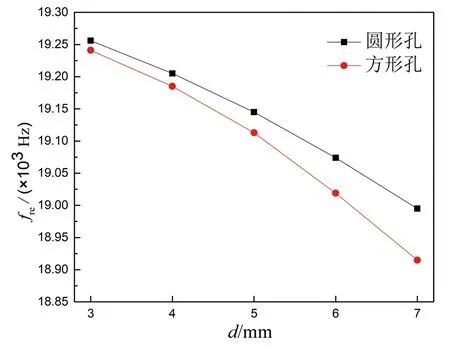
图10 fre随孔形、孔径的变化关系(N=9个,L=7 mm)

由图10可以看出，换能器的共振频率随N,d,L的增加而减小，且由方孔引起的共振频率的变化比圆孔更显著[12].

选取孔数N=9个，孔径和孔深皆为5 mm，对不同穿孔位置换能器模型进行仿真计算，得到各模型特征频率对应的振型如图11和图12所示.由图11和图12可观察到：相同参数下，孔形与穿孔位置对换能器的共振振型无明显影响，皆为轴向纵振动；节面处穿孔对换能器共振频率的影响大于其他位置穿孔，表现为穿孔后共振频率更低.

图11 横向穿孔压电换能器基频共振模态(圆孔,N=9个,d=5 mm,L=5 mm)

图12 横向穿孔压电换能器基频共振模态(方孔,N=9个,d=5 mm,L=5 mm)

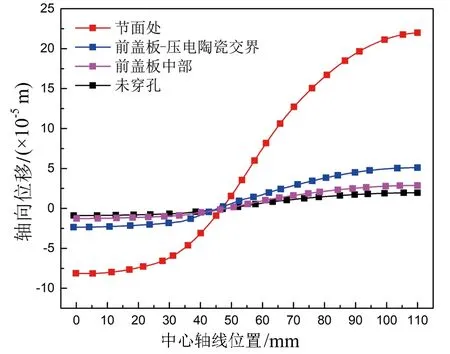
图13 轴向振动位移随穿孔位置的分布关系

2.2 穿孔对换能器轴向位移分布的影响

为更进一步说明横向穿孔换能器沿轴向振动位移分布，以圆形穿孔为例，定义换能器后盖板为坐标轴原点，沿轴线提取其振动位移.选取穿孔参数N=9个,d=7 mm,L=3 mm，图13为不同穿孔位置所引起的换能器端面输出位移振幅的变化.由图13可知，节面处穿孔可使换能器输出端面位移振幅有较大增益，这可能是因为穿孔形成了类似后短前长“哑铃式”变幅器结构[13]而造成的.

3 结 论

1)建立了无穿孔厚电极换能器的等效电路模型，对其进行了理论与仿真研究.结果表明：厚电极换能器的有效机电耦合系数随电极厚度增加而减小，理论与仿真结果吻合较好.

2)基于数值仿真计算,探讨了换能器共振频率、有效机电耦合系数与端面输出位移振幅随穿孔参数的变化关系.结果表明：在换能器节面处、前盖板-压电陶瓷交界及前盖板中部穿孔，换能器共振频率与有效机电耦合系数随参数的增加而单调减小；方孔对换能器共振频率的影响较为显著.特别地，在换能器位移节面处穿孔可获得较高的位移振幅输出.

3)需指出，尽管在换能器的节面位置穿孔可获得较大的位移振幅，但该位置是应力腹点，穿孔会导致换能器的结构强度降低.因此，在实际工程应用中，应对穿孔参数及穿孔位置进行合理选择.