澳大利亚“高考”数学文化试题特征及其评析——以2017—2021年VCE进阶数学试题为例

唐恒钧，周雯馨

澳大利亚“高考”数学文化试题特征及其评析——以2017—2021年VCE进阶数学试题为例

唐恒钧，周雯馨

（浙江师范大学 教师教育学院，浙江 金华 321004）

基于对数学文化的理解，借鉴相关研究构建数学文化试题的分析框架．从试题结构及总体题型题量、数学文化试题占比、数学文化类型、融入试题方式和学生行为期望5个方面，分析澳大利亚VCE进阶数学试题中数学文化的考查情况，以期为中国数学文化试题的编制提供借鉴．研究启示：正确对待数学文化的考查，呈现多样化的数学文化试题，采用更加内在而自然的运用水平，提高对学生数学思维品质的关注．

数学文化；澳大利亚VCE进阶数学；试题分析

近年来，数学文化作为关于数学知识滥觞、嬗变和进化的一种兼具专业化和社会性的共有记忆、符号结构和理念系统，在数学教育和数学共同体内已经获得广泛认可[1]．《普通高中数学课程标准（2017年版2020年修订）》也明确提出“注重数学文化的渗透”“高考试题融入数学文化”等观点[2]．高考作为选拔人才的重要手段，要发挥对中学数学教育的导向作用，更要体现数学的文化价值[3]．但有研究表明，数学文化在高考试卷中的落实情况不容乐观，有的试题仅将数学文化素材作为试题背景来考查学生的数学能力[4]．澳大利亚数学课程重视数学文化，该国维多利亚州VCE考试（Victoria Certificate of Education）在全球具有一定的影响力，已有学者对VCE考试体系及数学教材[6–7]进行过分析，也有学者对澳大利亚全国数学统一评估试题中的数学文化[8]进行过分析．这里将进一步考察VCE进阶数学考试中数学文化试题的特征，以期为中国数学文化试题的编制提供借鉴．

1 研究对象与方法

1.1 研究对象的选取

VCE数学考试分为进阶数学（further mathematics）、数学方法（mathematical methods）和专业数学（specialist mathematics）3类．进阶数学偏向应用，内容浅显易懂；数学方法偏向理论，难度较大；专业数学的难度更高．3类试卷中进阶数学试题与数学文化的融合尤为突出，因此选取2017—2021年进阶数学试题为研究对象．

1.2 分析框架

VCE进阶试题中的数学文化可从试题结构及总体题型题量、数学文化试题占比、数学文化类型、融入试题方式和学生行为期望5方面加以分析．

由于研究者视角的多元化，不同学者对数学文化内涵的界定不同．一般而言狭义的“数学文化”是指数学的思想、精神、方法、观点、语言，以及它们的形成和发展；广义的“数学文化”还包括数学史、数学家、数学美、数学教育、数学与人文的交叉、数学与各种文化的关系等[9]．一般而言，数学教材、试题的数学文化研究以广义的内涵为主．已有学者据此提出数学文化的不同类型，如汪晓勤将其分为数学史、数学与生活、数学与科学、数学与人文、数学与艺术、趣味数学6类[10]．王建磐等将其整合为数学史、数学与现实生活、数学与科学技术、数学与人文艺术4个方面[11]．唐恒钧、张维忠将其分为数学史、数学与生活、数学与科技、数学与人文社会、数学游戏、数学与艺术体育等6类[8]．基于上述研究，将试题中的数学文化分为数学史、数学与生活、数学与科技、数学与人文艺术4类．具体界定借鉴祁平[3]和王建磐[11]的研究，在此不加赘述．

就融入试题方式而言，沈春辉等将运用数学史的方式分为点缀式、附加式、复制式、顺应式和重构式；其它数学文化的运用水平分为外在型和内在型[12]．唐恒钧等将试题中数学文化的融入方式统一为附加型和整合型两大类，其中整合型又分为可分离的数学文化和不可分离的数学文化两种[8]．基于以上研究，将数学文化融入试题方式分为附加型、可分离型和不可分离型．

就学生行为期望而言，结合喻平的研究及数学文化试题特征，将学生行为期望分为理解、迁移和创新[13]．理解是指在较为明确的背景下，领会其中的数学问题，对基础知识和基本技能的掌握与应用；迁移是指在较为复杂的情境中，采用多种规则或多种方法解决问题；创新是指学习者能够对问题进行推广、变式，能够提出合理的猜想并证伪或证实，能够解决开放性、探究性问题，能够适度生成超越教材范围的新知识，形成优良的数学学科思维品质．

因此，在试题分析过程中形成如表1所示的分析框架．

统计过程遵循如下标准：首先，以数学文化要素和试题为共同的分析单元，即当一个数学文化要素出现在不同题目时分别计数，一个题目中出现多种数学文化要素时也分别计数；其次，解答题含不同小问时，其学生行为期望也会不同，因此在统计中按小问计数．

表1 数学文化试题分析框架

2 VCE进阶数学试题中的数学文化

VCE进阶数学考试分两场进行，即VCE进阶数学考试1（VCE Further Mathematics Written Examination 1）和VCE进阶数学考试2（VCE Further Mathematics Written Examina- tion 2）．按照数学文化试题的分析框架，对2017—2021年10套VCE进阶数学的数学文化试题进行分析．

2.1 试题结构及总体题型题量

2.1.1 试题结构

VCE进阶数学考试1和考试2均分为两部分，第一部分是必做题，第二部分是选做题．必做题含两个模块：数据分析、递归与金融建模；选做题含4个模块：矩阵、网络与决策数学、几何与测量、图与关系．题型为选择题和解答题，考试1为选择题，考试2为解答题．

2.1.2 总体题型题量

2017—2019年与2021年的总体题型题量相同．具体地，考试1总分40，其中第一部分共24道选择题，每题1分，共24分；第二部分4个模块，每个模块8道选择题，学生任选两个作答，共16分．考试2总分60分，其中第一部分有6～9道解答题，共36分；第二部分4个模块，所选的两个模块有6～8道解答题，共24分．两次考试总分100．

2020年的题量与另外4年略有差异．具体地，其选做题由原来的4选2变为了4选1，但每次考试的总分没有变化．此外，考试1的第一部分增至30题，第二部分每个模块增至10题．考试2第一部分增至11题，第二部分每个模块依旧有3～5题．

2.2 数学文化试题占比

为考察VCE进阶数学试题融入数学文化的情况，对数学文化试题在整份试卷的占比进行统计．如表2所示，2017—2021年数学文化试题在整份试卷的总占比差别不大，均高达七至八成．考试2的解答题尤为突出，均体现了数学文化．就考试1而言，第一部分必做题的数学文化试题占比依旧较高；第二部分选做题随着难度的升高，纯数学题相应增多．总体而言，VCE进阶数学试题融入数学文化较多．

表2 数学文化试题占比

2.3 数学文化类型

近5年VCE进阶数学仅含有数学与生活和数学与科技两类数学文化试题．如表3，2017—2021年数学与生活类试题占比最大，仅有少量试题属于数学与科技，且比例不稳定．可见生活情境是VCE进阶数学试题的显著特色．在考试1中，几道选择题常常会共用一个背景；在考试2中，同一模块的几道解答题，也常常以情境发展的脉络展开，衍生出真实问题．如2018年考试2递归与金融建模模块，问题1中朱莉将一定金额存入储蓄账户，计算复利情况；问题2中朱莉取出一定金额为公司添置一辆汽车，为了纳税，计算汽车的折旧率；问题3是朱莉退休后将退休金投资，考虑不同方案的获利情况．这就将试题所考查的知识与能力渗透于问题解决的过程中，潜移默化地培养学生的数学核心素养．

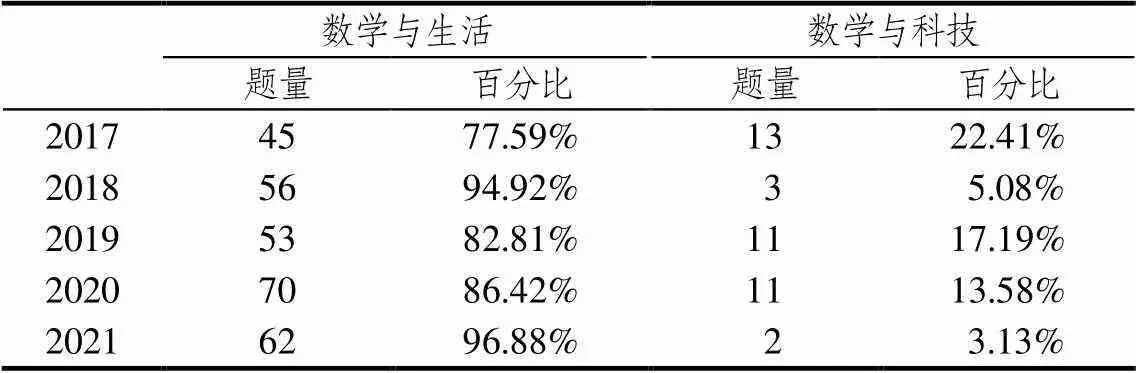
表3 数学文化类型占比

2.4 数学文化融入试题方式

对2017—2021年10套VCE进阶数学所涉及的数学与生活、数学与科技两类试题中数学文化融入方式进行分析（图1），发现两类试题均以不可分离型的融入方式为主，占比分别为53.85%、75.00%．这类试题着重强调用文化理解数学，或用数学解决文化中固有的问题．

图1 数学文化融入试题方式

如例1，亚历克斯是一名汽车修理师，若客户未在到期之前支付账单，他将会收取相应利息，依此来估计客户应支付金额．此类问题存在于日常生活中，是该情境中本应解决的问题，并非人为强加上去的．

例1 （2017考试2递归与金融建模题6）

亚历克斯修理完汽车后将帐单发给客户．若客户未在到期前付款将收取相应利息．逾期后对未支付账单每月收取1.5%的利息，按月复利计算．

a. 亚历克斯寄给马库斯200美元账单．

马库斯逾期一个月支付全部账单．马库斯共支付多少?

亚历克斯寄给莉莉428美元账单，她未在到期前付款．设A是逾期月的支付金额．

b. 用0、A+1和A写出一个递归关系来模拟账单金额．

c. 莉莉逾期4个月支付全部账单．莉莉支付多少利息？

其次是可分离型，占比分别41.96%、25.00%．这类试题往往是为解决其中的数学问题而人为强加于文化素材之上．如题目中已给出32名男性的身体质量指数，要求学生计算这组数据的中位数以及超重的比例等（2020考试2数据分析题1）．

仅数学与生活类试题涉及附加型的融入方式，占4.20%．如题目画出一个长方体盒子，并给出长宽高，要求学生计算盒盖的面积、盒子的表面积，并给出另一个与其相似的盒子，计算这两个盒子的体积之比（2017考试2几何与测量题1）．此题只不过指出这个盒子是美琪的储物箱，删去该文化要素对试题本身没有影响．

2.5 学生行为期望

VCE进阶数学解答题中不同小问对学生的行为期望逐步升高，考查每题达到的最高水平可以发现（图2），两类试题均在迁移水平占比最高，分别为51.98%、51.72%．

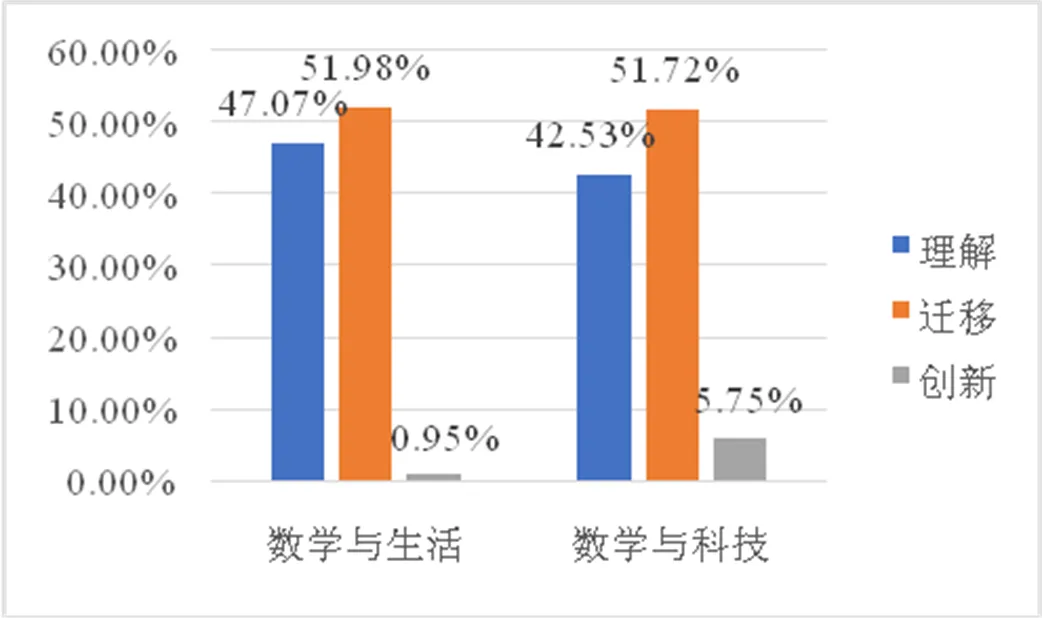
图2 学生行为期望

如例2，需要学生具备一定的阅读理解能力，将复杂情境中流浪猫及流浪狗的问题抽象为数学问题，正确理解3个变量间的相互关系及联系，以判断不同观点的正误．

例2 （2017考试1数据分析题12）

10年内所收集的数据表明，一个大型城市每年流浪猫和流浪狗的数量存在强正相关关系（=0.87）．该市人口与流浪猫数量（=0.61）及流浪狗数量（=0.72）也是正相关．数据收集期间，该市人口从34 564增至51 055，可得（ ）．

A. 若猫主人少养狗，则流浪猫数量就会减少．

C. 报告中流浪猫和流浪狗之间的数量关系未得到合理解释，这只是偶然现象．

D. 人口越多，流浪猫和流浪狗数量越多，流浪猫和流浪狗之间的数量关系可用共同的第三个变量解释，即该市人口增长规模．

E. 人们不像从前一样细心照料他们的猫，所以流浪猫越来越多．

其次是理解水平，占比分别为47.07%、42.53%．如例3，该题情境较为简单，学生只需运用网络与决策数学的基础知识即可解决问题．

例3 （2020考试2网络与决策数学题1）

阳光海岸板球俱乐部新加入5名球员：亚历克斯、波、卡梅伦、戴尔和埃莫森．图3显示在加入前彼此打过板球的球员．如亚历克斯和波之间的连线表示他们以前一起打过板球．

a. 在加入球队前有多少球员和埃莫森打过板球？

b. 在加入球队前，谁和亚历克斯和波都打过板球？

c. 又一新球员芬恩加入了球队，他没和任何球员打过板球．在图中表示该信息．

图3 例3插图

再次，处于创新水平的试题较少，占比分别为0.95%、5.75%．如例4难度较高，考查学生的数学思维品质，要求学生根据五分位数及箱型图探究最低日气温与月份的关联，这需要把握各种统计量的本质，灵活运用统计量做出合理猜想并给出理由．

例4 （2019考试2数据分析题3）

2017年2、5、7月最低日气温分布的五分位数汇总如表4，相关箱型图见图4（数据来源：澳大利亚政府气象局）．

为什么上述信息支持最低日气温与月份相关的论点，请借助适当的统计值作答．

表4 气温分布

图4 例4插图

3 结论与启示

研究发现，VCE进阶数学试题融入数学文化较多且题型多样，其中绝大部分属于数学与生活类，是该试题的一个显著特色；试题主要采用不可分离型及可分离型的融入方式；关注学生的知识理解和迁移水平，强调应用知识解决现实生活中的数学问题．基于上述分析，在对数学文化试题的编制中可关注以下4方面．

3.1 正确对待数学文化的考查

当前，数学文化在高考试题中的落实情况不容乐观．有的试题仅是增添一些“文化”佐料来考查学生的数学能力．这种简单化的理解，不仅异化了数学文化的内涵，窄化了数学文化的外延，而且没有触及数学文化的精神实质，难以达到对数学文化的真正考查，无形之中增加学生的学习负担[5]．

学科核心素养的提出，强调教学目标从以知识教育为重心转向以素养教育为核心．无论是数学课堂教学，还是数学考试都应切实站在学生的立场，坚持立德树人的教育思想，用数学文化去关心人与自然和社会的和谐发展[3]．这样才能更好地理解并把握数学文化，发挥其对学生数学精神、理性思维等潜移默化的作用．

3.2 呈现多样化的数学文化试题

VCE进阶数学中的数学文化试题较多且题型多样．其选择题与解答题均有涉及，但绝大部分是数学与生活类试题，数学与科技类试题较少，没有涉及数学史和数学与人文艺术．近年来，中国愈加关注高考融入数学文化并已取得一定成果，但也存在着一些问题．如数学文化试题数量较少；题型较为单一，多以选择题和填空题为主；数学文化类型单一，大多数为数学史和数学名题等．中国作为“文明古国，礼仪之邦”，应充分发挥其优势，挖掘更多数学文化素材，借鉴VCE进阶试题生活情境的经验，呈现更加多样化的数学文化试题．如结合数学史、著名古建筑、雕塑绘画、学生日常生活、当前新冠肺炎疫情、最新科技前沿等蕴含的数学元素来设计问题．利用民族数学促成感性体验向理性思维的转变[14]，这样既有助于拓宽学生的数学文化视野，也有助于学生形成较为全面的数学文化观．

3.3 采用更加内在而自然的运用水平

第一，使用科学严谨、真实的数据设置情境，以增强问题的真实性．VCE进阶数学考试有一个必做模块是数据分析，该模块涉及大量数据，这些数据科学严谨且真实．比如有的数据来自TomTom公司、澳大利亚政府气象局、国际奥委会等．使用真实的数据，一方面可以体现数学学科的严谨性，另一方面也可以让学生更好地体会数学的应用价值．

第二，试题以情境发展的脉络加以呈现，并在情境发展过程中衍生出真实问题．VCE进阶数学很多模块的几道解答题以情境脉络为出发点，衍生出与考查目标相关的问题，用问题链来联系每道题目，层层递进．这种试题编制方式有以下优点：首先，真实的情境拉近了学生与试题的距离，让人感受到问题随情境的发展而变化，充满人性化；同时能引起学生思考并激发学生解决问题的欲望．其次，模块的几道解答题逐步深入，学生每解决一个问题，并不意味着结束，而是自然地又衍生出一个新问题；实现了数学双基、问题解决、数学思维和数学精神目标的统一[15]．最后，试卷中的题目不是孤立的个体，而是密切相关、层层递进的整体，一来体现试卷的结构化、逻辑性，二来有助于学生数学核心观念的形成．

第三，采用不可分离型的融入试题方式以密切数学与人类其它子文化的联系．VCE进阶数学考试中，大量试题以现实生活为背景，数学文化不再是试题的“点缀”，而是让学生感受到数学既根植于文化，又促进文化的发展．提升学生通过文化理解数学和用数学解决文化中固有问题的能力，展现数学文化的工具价值、认识价值和文化价值．高考试题的编制也应真正立足于数学文化的本质，而非呈现长篇大论的数学文化素材，应是将数学文化“隐性化”，切实考查学生的数学核心素养．

3.4 提高对学生数学思维品质的关注

经研究发现VCE进阶数学考试旨在培养应用型人才，更注重基础知识和基本技能的掌握与应用．而中国高考作为选拔型考试，在关注基础知识与基本技能的同时，更要关注学生数学精神、理性思维和创新能力的培养，这是核心素养教育的一项重要任务．创造性思维是学生应对未来多变世界的必备素养，是数学课程标准所确立的重点课程目标，因此在高考试题的编制中，应依据学生创造性思维发展的心理特点，在学生创造性思维的“最近发展区”提供相应的数学任务[16]，培养学生的数学高阶思维能力．

总之，随着课程改革的推进，人们越来越认识到数学文化对数学教育的重要价值．但数学文化还存在着低应用的问题，如何考查、考查什么需要引起注意．通过对VCE进阶数学的数学文化试题进行统计分析，旨在探索其特征和规律，为中国数学文化试题的编制提供一些合理化的意见和建议．

[1] 黄秦安．数学文化视域下数学课堂模式的多元建构[J]．数学通报，2021，60（8）：11–15．

[2] 中华人民共和国教育部．普通高中数学课程标准（2017年版2020年修订）[M]．北京：人民教育出版社，2020：10．

[3] 祁平，任子朝，陈昂，等．基于数学文化视角的命题研究[J]．数学通报，2018，57（9）：19–24．

[4] 张维忠，孙庆括．我国数学文化与数学教育研究30年的回顾与反思[J]．当代教育与文化，2011，3（6）：41–48．

[5] 李祎．别被理念绑架教学[J]．数学通报，2019，58（2）：18–20，25．

[6] 章勤琼，麦克斯·斯蒂芬斯．澳大利亚“新高考”制度评析及启示[J]．外国中小学教育，2015（7）：30–35．

[7] 张笑谦，胡典顺．中澳高中数学教材的比较及启示——以澳大利亚VCE课程与人教版高中数学教材函数与映射章节为例[J]．数学教育学报，2013，22（2）：71–75．

[8] 唐恒钧，张维忠．澳大利亚数学统一评估试题中的文化研究[J]．数学通报，2016，55（3）：7–11．

[9] 顾沛．数学文化[M]．北京：高等教育出版社，2008：1–2．

[10] 汪晓勤．主要国家高中数学教材中的数学文化[J]．中学数学月刊，2011（5）：50．

[11] 王建磐，汪晓勤，洪燕君．中、法、美高中数学教科书中的数学文化比较研究[J]．教育发展研究，2015，35（20）：28–32，55．

[12] 沈春辉，柳笛，汪晓勤．文化视角下“中新美法”四国高中数学教材中“简单几何体”的研究[J]．数学教育学报，2013，22（4）：30–33，102．

[13] 喻平．数学关键能力测验试题编制：理论与方法[J]．数学通报，2019，58（12）：1–7．

[14] 唐恒钧，陈碧芬．基于民族数学的学生理性精神培养[J]．浙江师范大学学报（自然科学版），2019，42（3）：356–360．

[15] 唐恒钧，李婉玥．指向核心素养的小学数学文化主题活动及设计要点[J]．浙江师范大学学报（自然科学版），2021，44（4）：475–480．

[16] 丁福军，张维忠．创造性思维在数学教材中的呈现研究——以人教版小学数学教材为例[J]．浙江师范大学学报（自然科学版），2021，44（2）：234–240．

声 明

《数学教育学报》与中国知网、万方数据知识服务平台、超星、维普网、中国人民大学复印报刊资料库等合作，投稿的同时，我刊认为作者自愿将其拥有的对该论文的汇编权（论文的部分或全部）、翻译权、印刷版和电子版的复制权、网络传播权和发行权转让给编辑部．若有异议，烦请来信告知．

Analysis and Suggestions on Propositional Characteristics of Mathematics Culture in the Higher School Certificate in Australia——Talking VCE Further Mathematics from 2017 to 2021 for Example

TANG Heng-jun, ZHOU Wen-xin

(College of Teacher Education, Zhejiang Normal University, Zhejiang Jinhua 321004, China)

Based on the understanding of mathematics culture and referring to the relevant research, the analytical framework of mathematics culture test questions is constructed. In order to provide some reference for the proposition of mathematics culture text questions in China, this paper analyzes the mathematics culture text questions in VCE Further Mathematics from the following five aspects: the structure of the questions and the overall question type, the proportion of mathematics culture text questions, the types of mathematics culture, the way of integrating the test questions and students’ behavior expectations. Research implications: treating the examination of mathematics culture correctly, presenting a variety of mathematics culture text questions, adopting mathematics culture more internally and naturally, and increasing the attention to the quality of students’ mathematical thinking.

mathematics culture; VCE further mathematics; test analysis

G40–059.3

A

1004–9894（2022）06–0070–05

唐恒钧，周雯馨．澳大利亚“高考”数学文化试题特征及其评析——以2017—2021年VCE进阶数学试题为例[J]．数学教育学报，2022，31（6）：70-74．

2022–08–06

全国教育科学“十四五”规划教育部重点课题——指向深度理解的“问题链教学”研究（DHA200318）

唐恒钧（1979—），男，浙江余姚人，教授，博士后，博士生导师，主要从事数学课程与教学研究．

[责任编校：周学智、张楠]