中国初中数学课程中的变革能力与2030能力发展——基于OECD“学习框架2030”的课程图谱分析

孙学敏，唐海军，曹一鸣

中国初中数学课程中的变革能力与2030能力发展——基于OECD“学习框架2030”的课程图谱分析

孙学敏1，唐海军1，2，曹一鸣3

（1．贵州师范大学 数学科学学院，贵州 贵阳 550025；2．四川文理学院 数学学院，四川 达州 635000；3．北京师范大学 数学科学学院，北京 100875）

OECD学习框架2030为帮助学生应对未来世界的不确定性，创造美好的未来，定义了3种学生必备的“变革能力”．“面向2030能力发展”同时被提出．研究围绕OECD教育2030项目的最新研究：课程内容图谱分析项目，主要关注数学学科中变革能力与2030能力发展，梳理数学学科中对应的能力，采用内容分析法对中国数学课程中的变革能力与2030能力发展从总体分布和内容关联两个方面进行深入分析，得到一些启示和建议．

OECD“学习框架 2030”；数学课程图谱；初中数学课程；变革能力；2030能力发展

1 问题提出

经济合作发展组织（OECD）于2015年启动了“教育2030：未来的教育与技能2030”项目，2018年发布了“学习框架2030”．“OECD学习框架2030”为帮助学生在急剧变革的世界上茁壮成长，开创更好的未来，定义了3种学生所必需的“变革能力”（transformative competencies），即创造新价值的能力、调和矛盾和困境的能力、承担责任的能力和“面向2030的能力发展”（competency development for 2030），即预期能力、行动能力、反思能力[1-4]．

研究围绕OECD教育2030项目的最新研究：课程内容图谱分析项目（curriculum content mapping，简称CCM），主要关注变革能力与2030能力发展，梳理数学学科中对应的能力，采用内容分析法对中国初中数学课程中的变革能力与2030能力发展从总体和内容主题关联两个方面进行分析，以期为中国义务教育数学课程标准修订与教材编写提供借鉴，为教育工作者在课程教学中融入相关能力提供参考．

2 “OECD学习框架2030”下变革能力与2030能力发展的内涵

“OECD学习框架2030”在“核心素养项目”（DeSeCo1项目）所提出的“OECD关键能力”基础之上[2]，定义了3种学生面向未来必需的“变革能力”：创造新价值的能力、调和矛盾和困境的能力、承担责任的能力和“面向2030的能力发展”，即预期能力、行动能力、反思能力[1-4]（见表1）．

“OECD学习框架2030”的主要体现形式是OECD学习罗盘2030（OECD learning compass 2030）．罗盘由磁针和方向盘构成，其中，“变革能力”和“预期—行动—反思”起到“方向盘”的作用．在起航驶向“幸福2030”的过程中，磁针指明方向，而方向盘起着控制自我转向的作用，也是学生与航行器沟通的桥梁．

表1 变革能力和2030能力发展的定义

注：来源于OECD_Learning_Compass_2030_Concept_Note_Series. Paris: OECD, 2019.

3种变革能力有助于学习者在复杂的和不确定的情境中航行，属于更高水平的能力．创新是一切个体成长和可持续发展的核心能源．为了迎接无法预测却又充满挑战的未来，个体应该学会识别新的增长来源从而为社会增值．勇于承担责任的能力是创造新价值、调和矛盾和困境的先决条件，个体拥有该能力可以为实现个人幸福和集体福祉产生有诚信、有原则的行为，能够被他人信赖，委以重任．个人必须学会成为系统思考者，协调、解决工作生活中可能出现的各种矛盾、冲突或困境．三者彼此之间相互关联，相互作用，并随着情境的改变和个体经验的增长发生变化，使个体受益终生．

预期—行动—反思（anticipation-action-reflection，简称AAR）是能力发展的过程与周期，它是发展和形成变革能力的“催化剂”[4]．AAR基于建构主义，是有序循环的持续学习过程．行动本身的性质是中立的，它可能会对个人、社会或人类带来任何后果，有可能是积极的，也有可能是消极的．正因如此，行动的实施需要有目的性和责任感——所以要有预期在前，反思在后．反思保证了AAR循环的持续性．学习者自觉地计划、实践、反思，不断循环，不仅促进该领域特殊能力的形成，也有助于形成以上3种变革能力，最终开创个人和社会幸福的未来．

3 数学课程中变革能力与2030能力发展的体现

CCM将学校课程划分为7个学习领域[5]，数学是其中的一个重要领域．OECD学习框架2030下的变革能力与2030能力发展属于跨越学科的“一般能力素养”．在整体框架下结合数学学科的特点，对数学学科情境中的变革能力与2030能力发展作进一步解析，有助于深入理解各项能力素养．

3.1 数学课程中的变革能力

中国现代数学教育将创新意识的培养作为育人的基本任务，《义务教育数学课程标准（2011年版）》（以下简称《课标（2011年）》）将创新能力作为设计思路的10个核心词之一．数学创新能力存在于数学学习的每个环节和整个过程，它与数学创造性思维有着紧密的联系．

数学学习的本质是数学思维活动的过程．在数学创造的过程中，必然会发生思维的碰撞，产生困惑甚至经历失败．强烈的责任感是面对挫折、战胜困难的内驱力．数学学科中的承担责任还体现在思维活动过程中所表现出的情感、态度和价值观．例如，《课标（2011年）》中“形成坚持真理、修正错误、严谨求实的科学态度”；“如何让学生做自己能做的事，并对自己做的事情负责”[6]．

数学学习过程不仅是学生个体的成长过程，也是学生与社会互动的过程．解决问题是一种数学学习的过程．而解决数学问题的本质是社会建构，将个人主观数学认知转化成使人接受的客观数学知识，需要社会性的交流和合作[7]．在数学学习的过程中，这一社会性技能体现在：在合作解决数学问题的过程中避免仓促地给出一个单一的答案，或只找到一个非此即彼的解决方案，而是要处理多元化带来的紧张、两难和权衡．例如，《课标（2011年）》中“如何引导学生善于与同伴合作交流，既能理解、尊重他人的意见，又能独立思考、大胆质疑”；“在与他人合作和交流过程中，能较好地理解他人的思考方法和结论”等[6]．

3.2 数学课程中的2030能力发展（AAR）

在数学学科情境中，预期是行动前的预判，比如，数据处理前的数据直觉，以及数据分析过程中的预测、模拟、推断等关键能力；预期同样反映了学生个体在应对未来新情境和新挑战时所具备的情感和态度，如对未来充满信心、产生负责任的行动．《课标（2011年）》指出：“知道通过大量地重复试验，可以用频率来估计概率”；“通过表格、折线图、趋势图等，感受随机现象的变化趋势”等[6]．

行动，在数学学科中指经历数学活动的过程，学习者在此之中积累数学基本活动经验，发展实践能力．在数学教育教学中，活动始终贯穿于其中．学生在尝试性的数学活动中“创造”出自己的数学，同时，数学活动也是发展其数学核心素养的必要条件．中国《课标（2011年）》课程目标中，将“基本活动经验”明确地列入“四基”之中，并指出，“积极参与数学活动，对数学有好奇心和求知欲”；“体验数据收集、处理、分析和推断过程，理解抽样方法，体验用样本估计总体的过程”等[6]．

基于数学作为思维学科的特点，数学为反思提供了大量的思维内容，反思为数学建构了更完善的知识体系和思维方式[8]．《课标（2011年）》指出，“能针对他人所提的问题进行反思，初步形成评价与反思的意识”等[6]．

4 基于CCM的变革能力与2030能力发展分析

中国数学课程内容图谱研究团队依据官方资料“CCM正式研究指南”“CCM数学内容编码框架”“CCM正式研究能力框架”等，结合中国初中阶段数学课程特点形成编码手册，采用质性文本分析方法对《课标（2011年）》中的初中部分进行编码分析，识别现有课程内容和内容编码框架的匹配程度，并依据项目组提供的4级赋分规则，以内容主题框架中的子主题为单位，判断现有课程中各内容条目所对应的能力素养培养要求，从而进行能力要求等级赋分[9]．具体赋分规则如表2．

表2 数学CCM赋分规则

研究团队将上述6项能力素养整合进与数学内容编码框架相匹配的23条初中数学课程内容主题，形成了138个“内容—能力”二维关联单元．然后以二级数学内容主题为单位，根据表2所示CCM赋分规则，进一步分析识别每个单位所涉及的能力素养的层次，最终形成关于2030能力素养的识别以及内容与能力的二维关联分析等结果[9]．以下根据研究团队前期的分析结果，从能力的总体分布和内容关联两个方面对中国初中数学课程中的变革能力和2030能力发展作进一步阐释，并得出结论．

4.1 结果与分析

4.1.1 总体分布分析

根据上述形成的138个“内容—能力”二维关联单元能力素养的赋分结果，分别统计创造新价值的能力、调和矛盾和困境的能力、承担责任的能力、预期能力、行动能力、反思能力6种能力素养各分值所占的比例，结果如图1所示．

由图1可以看出，3种变革能力和2030能力发展在中国初中数学课程中均有涉及，但所要求的程度不同．其中，创造新价值的能力、承担责任的能力、调和矛盾和困境的能力赋分均为2．在课程标准中，这3种能力在前言、课程目标、课程实施建议和附录中笼统出现，没有关联具体数学内容．原因可能是，在中国初中数学课程中，认为这3种变革能力是学习者通过学习广泛而全面的具体数学内容之后，逐渐形成的更高水平的能力素养．

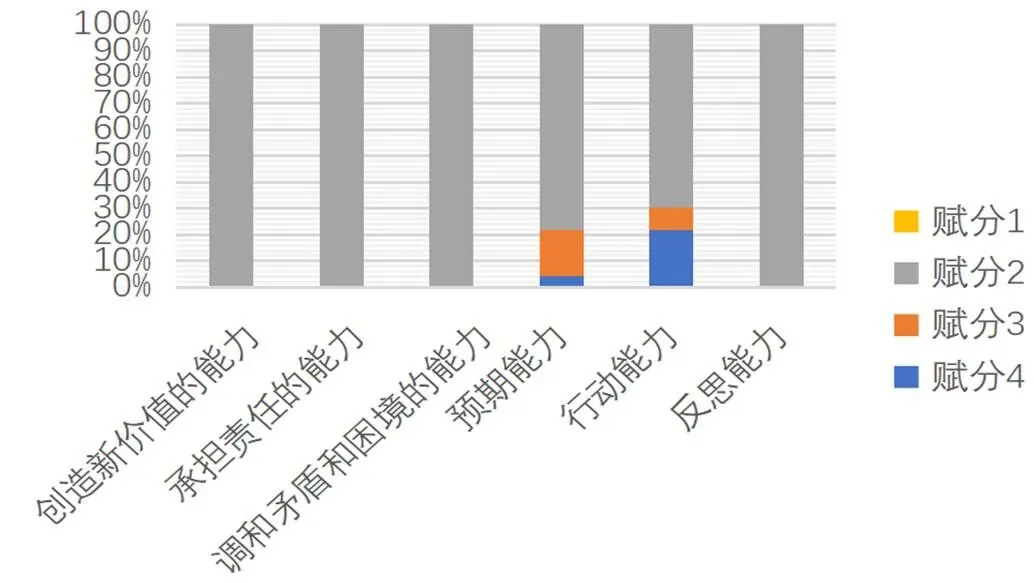
图1 变革能力与AAR赋分占比

对于2030能力发展，具体预期能力和行动能力而言，作为主要目标呈现，要求赋分为4的条目占比分别为4.3%和21.7%；作为次要目标呈现，要求赋分为3的占比为17.4%和8.7%．可见，行动这一能力素养作为主要目标呈现所占比重相对较多，预期能力次之．说明中国数学课程较重视学生的行动能力．如前所述，行动能力体现在数学课程中，指学生经历数学的活动过程．中国数学课程中长期存在着一些问题，如重书本知识传授，轻实践能力培养；重学习结果轻学习过程；重间接知识的学习，轻直接经验的获得；重教师的讲授，轻学生的探索[10]，中国在进入新课程改革后，数学课程开始逐渐重视让学生经历学习和探索的过程，强调直接经验的获取和实践能力的培养．在《课标（2011年）》中将“数学基本活动经验”与“基础知识”“基本技能”“基本思想”并列为“四基”作为课程目标被提出，并设置了“综合与实践”模块作为课程内容的一部分，目的在于积累学生的基本活动经验，提高实践创新能力．反思能力的要求赋分为2，在前言、课程目标、课程实施建议和附录中笼统出现，没有关联具体数学内容．

4.1.2 内容关联分析

数学课程中能力的发展要以数学核心内容为载体．国际数学课程图谱分析项目在确定数学学科的“学习内容”时，尽量使选定的数学内容能够覆盖世界不同地区（如亚洲、美洲、欧洲等）的数学课程，最终形成了“CCM数学内容主题框架”．内容框架共包括7类内容主题：（1）数（number）；（2）测量（measurement）；（3）数据和概率（data and probability）；（4）表达式、方程和代数（expressions, equations and algebra）；（5）函数（function）；（6）几何（geometry）；（7）数学通识部分（general description, where relevant）．上述内容主题共包含31项子主题，其中与中国初中数学课程内容匹配的子主题有23项[11]．进一步分析31项子主题下内容与能力的二维关联结果，有助于厘清变革能力和2030能力发展与中国数学课程内容主题的整合情况．

（1）数．

内容主题“数”包含7项子主题（如图2所示）．其中“MNU3复数”“MNU5分数和小数相关问题解决中的计算策略”“MNU7基于向量的建模和运算”在中国初中数学课程中不涉及，MNU3、MNU7将在高中阶段学习，MNU5在小学阶段学习．另外4项子主题与中国初中数学课程内容完全或部分匹配．变革能力与2030能力发展对这4项子主题的赋分均为2，在课程标准中没有关联到具体“数”的内容，换言之，“数”内容主题没有将变革能力与2030能力发展作为主要或次要培养目标进行整合．“数”对于整个数学课程乃至其它学科、日常生活和工作都是重要的基础，中国历来重视“双基”的培养，并强调发展学生的数感、运算能力．变革能力与2030能力发展，是学生掌握了牢固的“双基”之后发展的更高水平的能力素养．

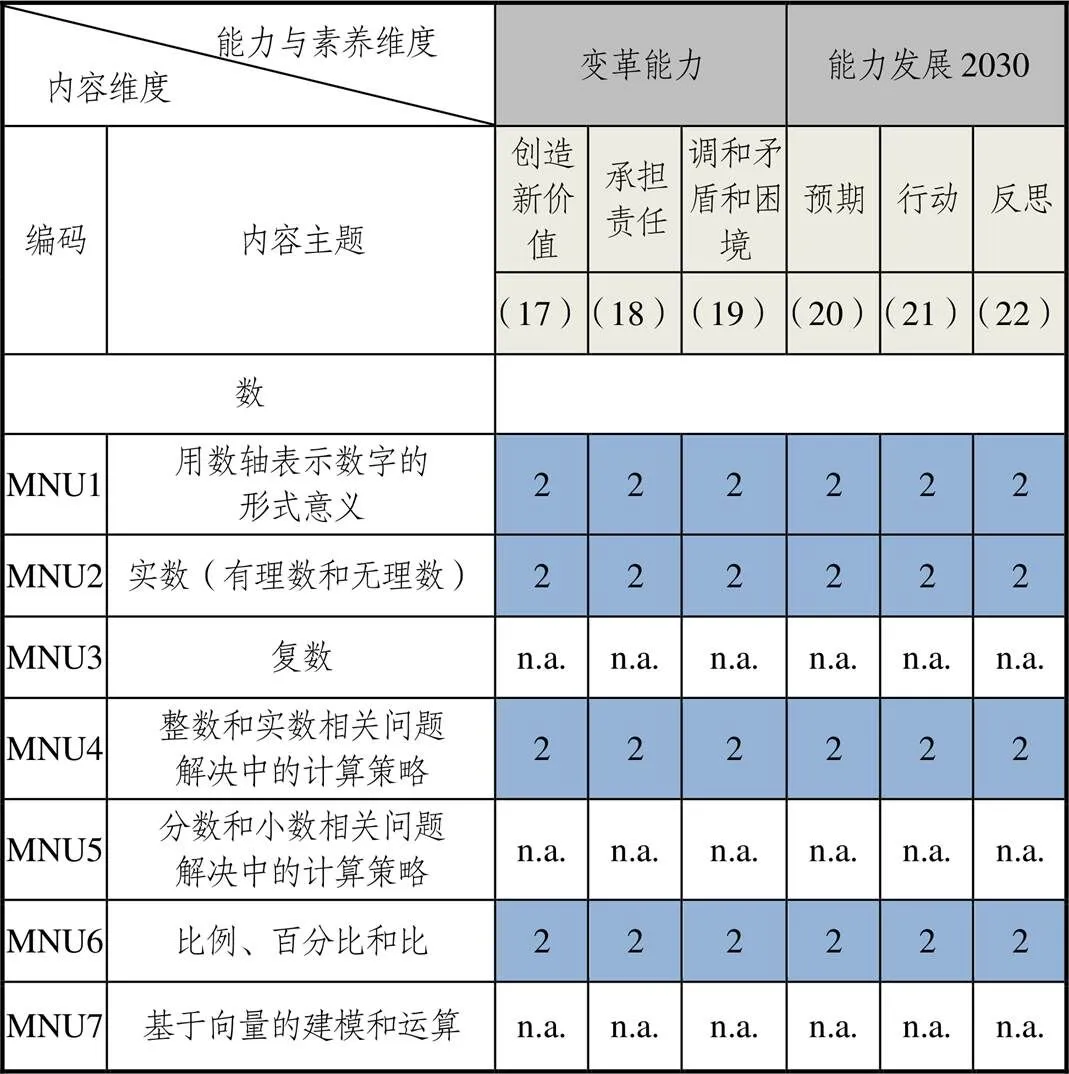
图2 “数”内容与能力二维关联图

（2）测量．

内容主题“测量”仅包含“MME1度量单位和比例尺”内容，在中国初中阶段数学课程中无涉及（如图3所示），原因在于中国这部分内容在小学阶段学习，具体对应一至六年级“图形与几何”中的“分类和度量”．这是否间接地反映了中国小学阶段“图形与几何”内容领域难度较大，还需通过国际比较研究作进一步探讨．

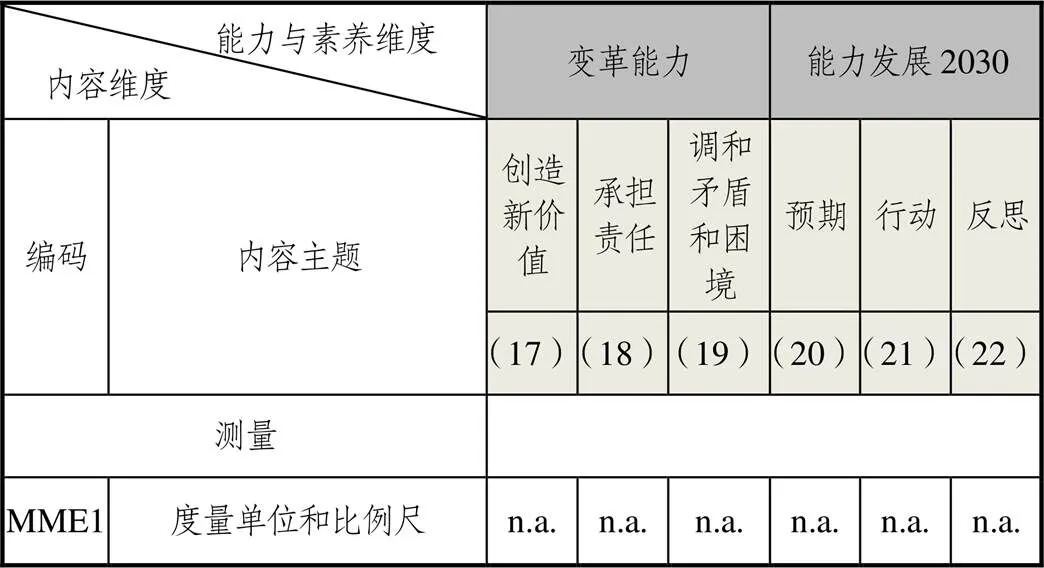
图3 “测量”内容与能力二维关联图

（3）数据和概率．

内容主题“数据和概率”共含7项子主题（如图4所示），其中“MDP6线性模型”“MDP7双变量关联（相关）”在中国初中数学课程中不涉及．由图4可以看出，形成的“内容—能力”二维关联单元赋分为2或3．表明6种能力素养在5项子主题中都有所体现，体现的程度不同．对于赋分为3的关联单元，预期能力作为次要培养目标被整合在3个二级内容主题中，分别为“MDP2整理、展示和解释数据”“MDP3随机过程”“MDP4概率模型”．这3个子主题的学习都涉及对数据的预测、模拟、推断等做出计划的过程，与此密切相关的能力素养是预期能力，因此课程标准中明确关联了这3项子主题．

特别地，对于子主题“MDP2整理、展示和解释数据”，目标是培养学生的数据分析与处理能力，为了使学生真正地感知数据、亲近数据，最好的办法就是让学生亲历数据的收集、整理、描述、分析以及做出决策的全过程，并在此过程中发展学生的数据分析与处理能力，因此该内容主题同时将行动能力作为次要培养目标进行了整合．3个变革能力在课程标准中没有关联到具体的“数据和概率”内容．

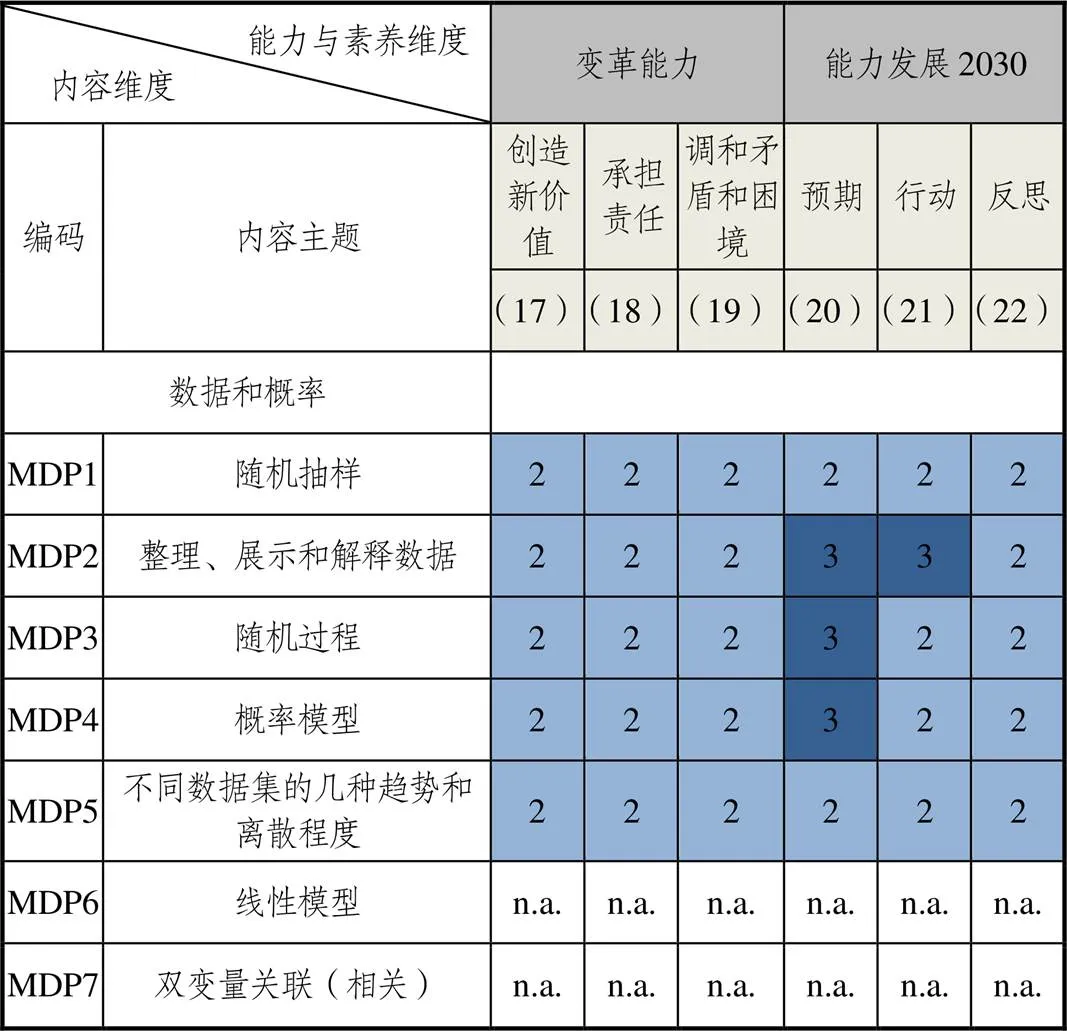
图4 “数据和概率”内容与能力二维关联图

（4）表达式、方程和代数．

内容主题“表达式、方程和代数”包含5项子主题（如图5所示），中国初中数学课程中对这5项子主题都有涉及．由图5可以看出，6个能力素养与5项子主题形成的30个“内容—能力”二维关联单元赋分均为2，表明该内容没有将变革能力与2030能力发展作为主要或次要培养目标进行整合．在“表达式、方程和代数”内容中，中国数学课程仍然重视“双基”的培养，同时发展学生的符号意识、运算能力、推理能力、模型思想和应用意识．事实上，中国中学生之所以在国际测试中成绩斐然和中国学生在这一学段建立起来的扎实的“代数”基础是密不可分的．变革能力与能力发展2030在这里仍被看作学生掌握了牢固的“双基”之后发展的更高水平的能力素养，笼统地出现在《课标（2011年）》中，被视为初中课程实施过程中，教师需要创造机会渗透或者有可能进行培养的能力素养．

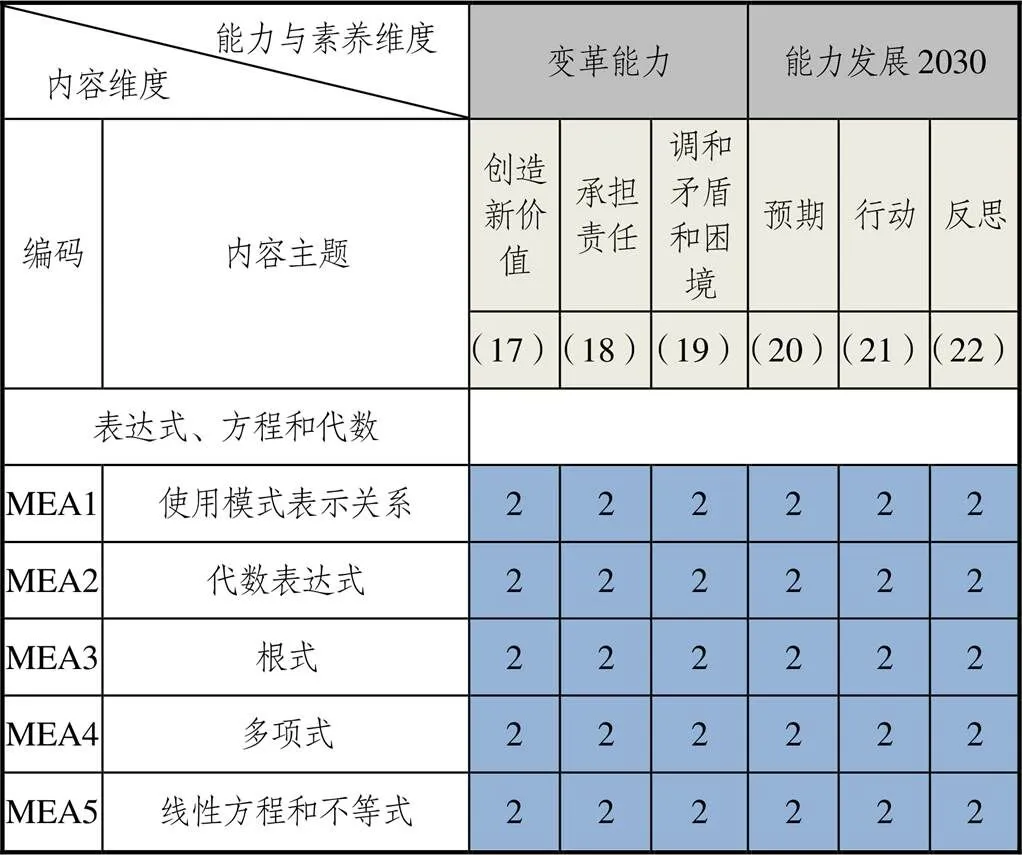
图5 “表达式与方程及代数”内容与能力二维关联图

（5）函数．

内容主题“函数”下，与中国初中数学课程内容匹配的子主题有“MFU1使用函数对关系进行建模”“MFU2二次函数”“MFU4三角函数”．“MFU3指数函数”在初中数学中不涉及，将在高中阶段学习．6个能力素养与3项子主题形成的18个“内容—能力”二维关联单元赋分均为2（如图6所示），6个能力素养课程标准中没有关联到具体“函数”的内容．“函数”在中国数学内容中属于“数与代数”领域，是沟通代数的桥梁，也是物理、化学等自然学科和解决生产生活实际问题时建模的基本工具，因此是初中数学的核心内容．中国数学课程非常重视“函数”这一核心内容，并注重在其中培养学生的运算能力、推理能力、模型思想和应用意识．变革能力与能力发展2030这类跨越学科的“一般能力素养”被视为初中函数课程实施过程中，教师需要创造机会渗透或者有可能进行培养的能力素养．

图6 “函数”内容与能力二维关联图

（6）几何．

内容主题“几何”中的3项子主题与中国初中阶段数学课程内容都完全匹配或部分匹配，包括：“MGE1空间关系（平面几何、空间几何的定理和性质）”“MGE2平面、空间中的几何旋转和变换，包括相似变换”“MGE3勾股定理”（如图7所示）．3项子主题都将行动能力作为主要培养目标进行了整合．几何内容在培养学生的推理能力、直观想象能力等方面有着至关重要的作用．20世纪初，在“培利—克莱因运动”中，培利主张：数学应当从欧式几何中解脱出来，给予实验几何充分的重视，更多地利用几何的直观性等．中国自建国以来经历了几次几何课程改革，都在逐渐增加实验几何、直观几何的内容．《课标（2011年）》在“几何”课程内容部分十分强调直观、实验操作以及对性质定理的探索活动，因此在“几何”内容主题中明确要求了行动能力．变革能力与AAR中的反思能力，在“几何”课程中没有整合具体的数学内容．

澳大利亚科学与数学学校（Australian Science and Mathematics School，Adelaide，South Australia）展示了一节课．这节课主要探讨伪科学论断并让学生考察什么证据能保证结论的真实性．课堂中教师在“圆和三角定理”的猜想和证明中运用了一个数学专用模型，从中学生学到了考察结论的真实性，以及什么证据才能证明结论的真实性．课堂中学生分组证明他们的结论．这有助于学生在一个真实情境中发展协调矛盾与困境的能力．这个教学案例对中国课程在“几何”内容主题中培养“调和矛盾和困境”能力提供了一些启示．如，在子主题“MGE1空间关系（平面几何、空间几何的定理和性质）”定理的猜想和证明活动中整合调和矛盾和困境的能力．

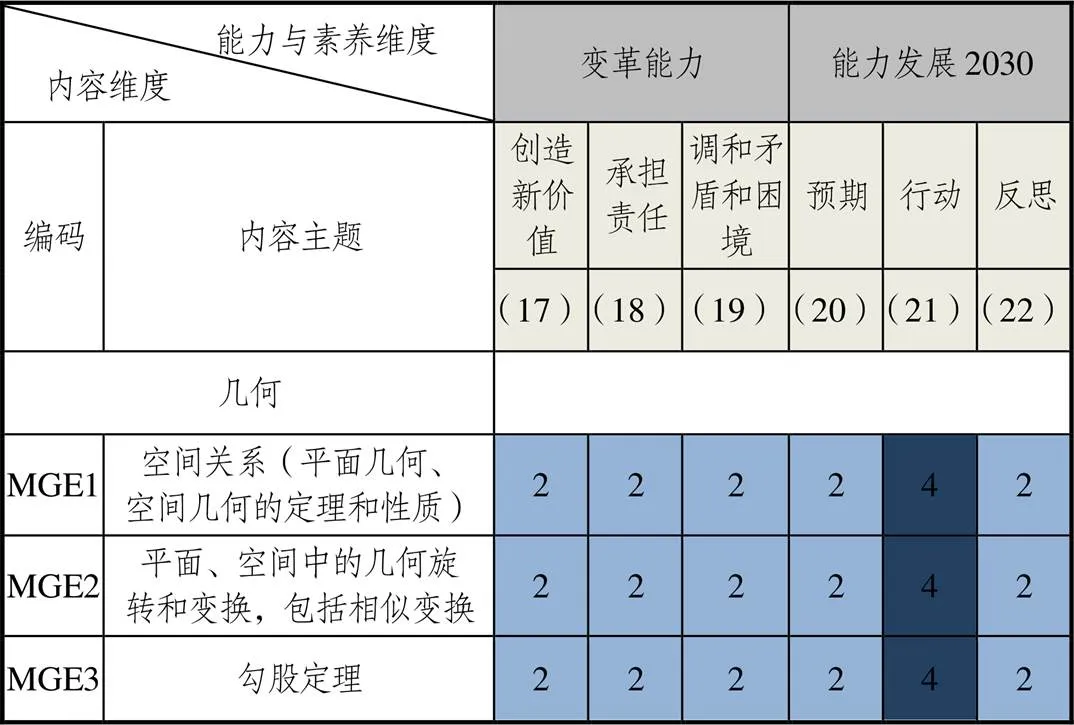
图7 “几何”内容与能力二维关联图

（7）数学通识部分．

内容主题“数学通识部分”中，包括4项子主题（如图8所示）．“MGE1”指会用数学的眼光看待世界，“做数学家的工作，像数学家一样思考”．“做数学家的工作，像数学家一样思考”并非要将学生培养成数学家，而是创造机会，让学生从事与数学家相似的数学思考和实践活动，从中体会数学如何对现实生活、现实世界发挥作用，数学如何与现实生活、现实世界产生联系．因此与“MGE1”子主题密切关联的是行动能力．对于“MGE2”，根据研究团队的解读，即学生在学数学、用数学的过程中应遵循一定的社会伦理、道德价值的规范，在初中数学课程标准前言至教学实施建议中有许多相关描述，表述虽不是很显性地展示了学生在学数学、用数学的过程中需要遵循的伦理和价值规范是什么，但教师可以创造机会在教学活动中整合并渗透．例如，区别样本与总体的关系、科学合理选择统计量、客观准确解读数据（不造假，不抄袭等）、以及在抽样调查和结果报告过程中遵循样本群体的保护原则，保护其隐私、名誉、减少干预与破坏等，这些均是教师在教学中有机会进行渗透的内容．因此，图中能力赋分2占大多数，包括3个变革能力和反思能力．

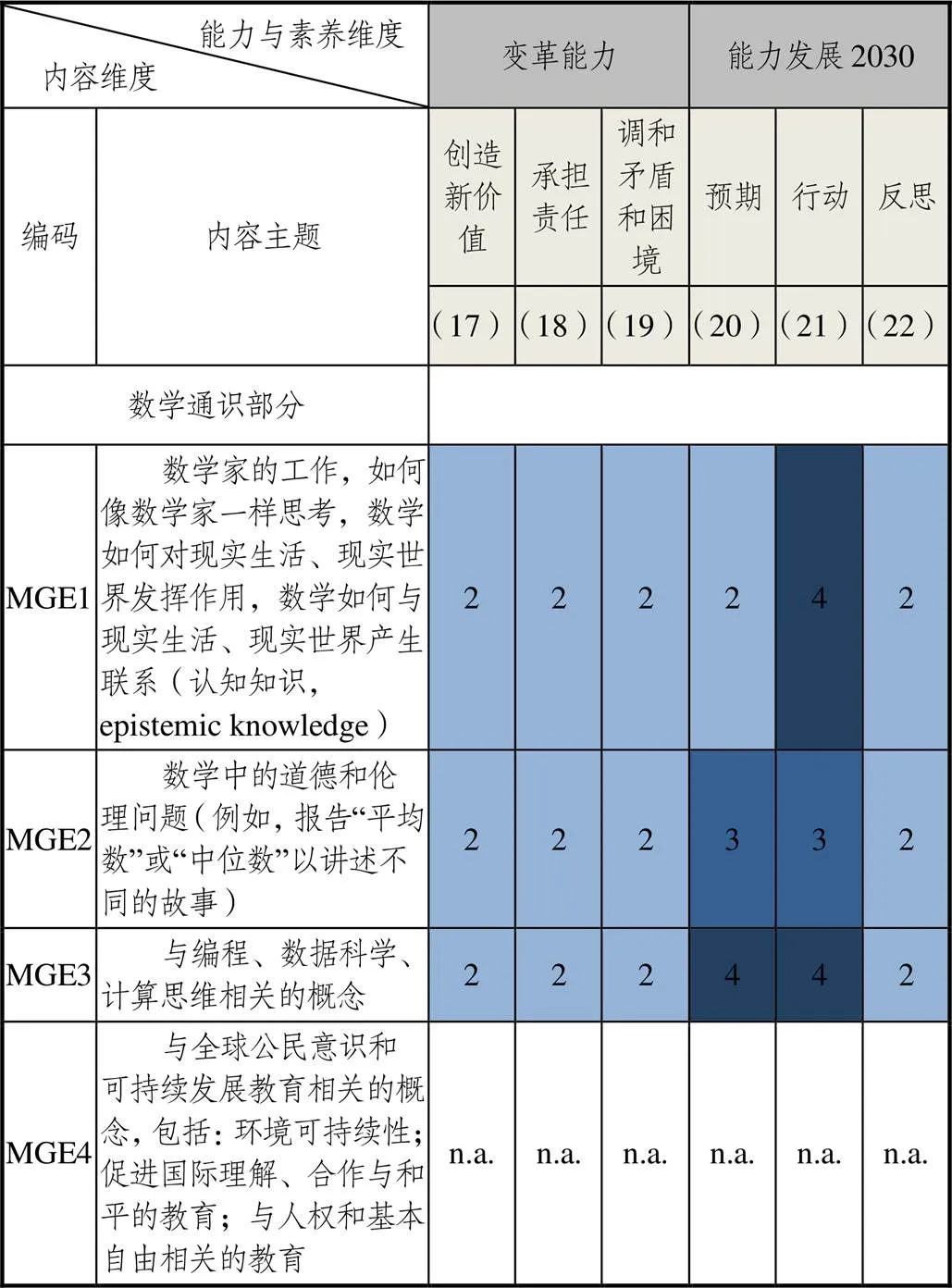
图8 “数学通识部分”内容与能力二维关联图

“MGE2”子主题中涉及“能解释统计结果，根据结果做出简单的判断和预测，并能进行交流”旨在发展学生的预期能力和行动能力．“MGE3与编程、数据科学、计算思维相关的概念”与中国初中数学内容对应较少，和编程、数据科学相关的算法等概念在高中阶段开始出现．编程、数据科学、计算思维与数学学习密切相关．其中，计算思维作为数学素养的一部分，要求学生综合使用数学思维和计算思维做出预测，为论证提供证据，并对不同的问题解决方案进行检验和比较．与中国数学课程对应的内容是经历数据的收集、整理、描述和分析过程，学会根据统计结果进行推断和预测，因此将预期能力和行动能力作为主要培养目标进行了较多整合．“MGE4与全球公民意识和可持续发展教育相关的概念”在中国初中阶段数学课程内容中不涉及，属于跨学科内容，主要在人类学（humanities）中学习．然而，全球公民意识和可持续发展教育是国际课程建设的重要内容，通过数学学习获得的知识和技能有助于学生探索可持续性问题及其解决方案．如，学生运用空间推理、测量、估计、计算和比较来衡量当地生态系统的健康状况，并为可持续性发展提出建议和措施；对社会、经济和生态系统随时间的变化进行衡量、追踪和量化；借助数据分析结果预测未来变化，进而在决策和采取行动中做出优化选择等[11]．学生运用数学知识技能探索和理解全球公民意识和可持续发展相关的概念时，学生需要负责任地行事，处理多元化带来的紧张、两难和权衡．促进理解和合作，创造新的增长点，为环境可持续性做出贡献，从而加速自身变革能力的发展．

4.2 研究结论

（1）变革能力与2030能力发展在中国初中数学课程中都有所体现，教师有机会在教学活动中整合并渗透，但绝大多数没有整合到具体的数学内容中．

OECD定义的6种能力素养在6类23项内容主题中都有不同程度地体现，形成的138个“内容—能力”二维关联单元赋分等级包括2、3、4，其中赋分2的关联单元占据大部分比例，说明大部分变革能力与2030能力发展目标在初中数学课程有所涉及，但课程标准仅在前言、课程目标、课程实施建议和附录中进行了笼统的能力素养要求，没有关联具体数学内容，是对教学活动的建议．或者课程标准中没有提及，仅在课程标准解读、教材、教参中提到，教师需要创造机会在教学活动中整合并渗透．

（2）“行动能力”作为初中数学课程主要培养目标受到较多关注，其次是“预期能力”，3种变革能力和反思能力没有整合到具体的数学内容中．

在6类23项内容主题中，作为主要目标培养的能力素养是“行动能力”，占比21.7%，预期能力次之，占比4.3%．说明目前中国数学课程较重视学生的行动能力．创造新价值的能力、承担责任的能力、调和矛盾和困境的能力等3种变革能力和反思能力没有整合到具体的数学内容主题中，课程标准仅在前言、课程目标、课程实施建议和附录中进行了笼统的能力素养要求．进一步通过能力与内容关联分析发现：与行动能力整合较多的内容主题依次为“几何”“数学通识部分”“数据和概率”．与预期能力整合较多的一级内容主题是“数学通识部分”和“数据和概率”．“数学通识部分”下的子主题“与全球公民意识和可持续发展教育相关的概念”这类跨学科内容的学习，有助于加速学生变革能力的发展，在中国初中数学课程中不涉及．

5 启示及建议

5.1 中国数学课程需进一步关注变革能力与2030能力发展

变革能力与2030能力发展是帮助学生应对未来各种不确定和挑战的能力与素养．中国数学课程已然意识到变革能力与2030能力发展的重要性，在课程标准中屡次提到“创新意识”，并将创新意识作为课程标准的十大核心词之一，其它5个能力素养也在课程标准中的前言、课程目标、课程实施建议、附录和课程内容部分，或课程标准解读、教材、教参中被不同程度地提到．面向2030新的时代背景，未来中国设计和开发以能力与素养为导向的数学课程时，应进一步关注新兴跨领域素养，重视培养学生的社会性技能．变革能力是复杂的，为促进这些能力的形成和发展，中国数学课程需要进一步结合具体的数学内容，给学生提供真实情境中体验学习的机会，注重知识与现实世界的联系[12]．

5.2 坚持能力目标与数学课程内容的整合

数学核心内容在学生能力与素养的培养以及世界观的形成上起着无法取代的作用．中国数学学科CCM以国际标准为参考、以证据为基础，对数学课程内容和面向2030学习框架能力与素养进行了二维关联分析．通过分析发现，中国应坚持将变革能力与2030能力发展与课程内容实施整合，具体体现为：进一步探索开发适合学生变革能力与2030能力发展的数学内容，如将“数学通识部分”的子主题“与全球公民意识和可持续发展教育相关的概念”这类跨学科内容整合在数学课程中，并注重变革能力在其中的融合．与时俱进地扩展更新时代性较强的数学知识，以知识主题为引领，全面落实“四基”．同时，应进一步将变革能力与课程内容深度融合．例如，在“几何”二级内容主题“空间关系（平面几何、空间几何的定理和性质）”中进一步整合变革能力．3个变革能力和反思能力在中国《课标（2011年）》中都没有关联到具体的数学内容．在课程内容标准中说明具体数学内容中需要发展的能力与素养，有助于指导教师找到更多的机会以能力与素养为导向实施教学，并基于显性的、可观测的能力与素养进行评价，同时确保内容标准的主体地位，发挥其对教学实施和评价的具体指导作用．如澳大利亚数学课程标准在课程文本表述时，在数学内容中把需要的一般能力用图标识出来，并有相应的注释以及对应数学学科的说明，教师会找到更多的机会以能力与素养为导向实施教学和评价．

5.3 在一般能力与素养框架下发展数学能力

纵观“教育2030：未来的教育与技能2030”项目整体，OECD学习框架2030阐述了学生面对充满变化且不稳定的新未来，携手创造“幸福2030”所需的关键能力及形成过程，为当今中国以能力与素养为导向的各学科课程设计提供了一个顶层框架．以国际标准为参照，在统一的课程能力与素养发展框架下设计数学学科课程目标与能力体系，有利于进一步发掘数学学科能力与素养的内涵和价值，培养学生的跨学科能力，使学生成长为“全面发展的人”[13-29]．中国应立足本土，同时紧跟国际，在OECD学习框架2030下对照看待中国的数学课程，寻找差距、弥补不足，做到扬长避短．

[1] OECD. The future of education and skills: Education 2030 position paper [R]. Paris: OECD, 2018.

[2] OECD. The future of education and skills: Education 2030, the future we want [R]. Paris: OECD, 2018.

[3] OECD. Transformative competencies for 2030 [R]. Paris: OECD, 2019.

[4] OECD. Anticipation-action-reflection cycle for 2030 [R]. Paris: OECD, 2019.

[5] OECD. Education 2030 curriculum content mapping: An analysis of the Netherlands curriculum proposal [R]. Paris: OECD, 2019.

[6] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：1-67．

[7] 喻平．数学教学心理学[M]．北京：北京师范大学出版社，2018：284-289．

[8] 常春艳，涂荣豹．探析数学反思性教学的特征及本质[J]．数学教育学报，2011，20（6）：8-10．

[9] 曹一鸣，马云鹏，郭衎，等．面向未来的初中数学课程图谱分析——以经济合作与发展组织（OECD）“学习框架2030”为基础[J]．基础教育课程，2020（10）：4-16．

[10] 裴娣娜，杨小微，熊川武．现代教学论[M]．北京：人民教育出版社，2005：1-455．

[11] 董连春，魏航，孙彬博，等．基于OECD“学习框架2030”的初中数学课程内容分析及其启示[J]．数学教育学报，2020，29（5）：1-6．

[12] 曹一鸣，朱忠明．变与不变：PISA2000—2021数学测评框架的沿革[J]．数学教育学报，2019，28（4）：1-5．

[13] 严虹．基于能力要求的初中数学课程国际比较研究[J]．教学与管理，2018（10）：80-83．

[14] 孙彬博，郭衎，邵珍红．PISA2021数学素养测评框架中的“21世纪技能”[J]．数学教育学报，2019，28（4）：12-16．

[15] 王罗那，唐彩斌，毛耀忠．芬兰初中数学《国家基础教育核心课程》评介及启示[J]．数学教育学报，2020，29（4）：62-67．

[16] 曹一鸣，宋宇，赵文君，等．面向教育2030的数学课堂对话人工智能评价体系构建研究[J]．数学教育学报，2022，31（1）：7-12．

[17] 李卓忱，汪晓勤．中法初中数学教科书章前页中的数学文化比较研究[J]．数学教育学报，2022，31（2）：26-34．

[18] 于文华，王光耀，蔡金法．基于BEA的个体问题解决干预有效性研究[J]．数学教育学报，2021，30（5）：28–32．

[19] 唐海军，严虹，任旭．数学合作问题解决视野下的“三教”探析[J]．数学教育学报，2021，30（5）：72–79．

[20] 张玉环，吴立宝，杜伟燕．法国普通中学数学教师资格考试述评[J]．数学教育学报，2021，30（5）：80–86．

[21] 郭衎，曹一鸣．知识与信念：基于学生表现的教师核心素养研究[J]．数学教育学报，2021，30（4）：1-5．

[22] 黄荣金，曹一鸣．中国数学教师合作学习的理论和实践：一个国际视角的审视[J]．数学教育学报，2021，30（3）：1-3．

[23] 丁莉萍．数学教师合作学习的理论与实践之比较分析[J]．数学教育学报，2021，30（3）：4-11．

[24] 曹一鸣，李信巧，郭转娜，等．初中数学教师非正式交流研究——基于中国3个地区七年级数学教师的调查分析[J]．数学教育学报，2021，30（3）：12-17．

[25] 陈肖颖，章勤琼，Shin Bomi．数学教师合作学习的效能研究——一个语义会话的分析[J]．数学教育学报，2021，30（3）：18-24．

[26] 黄兴丰，黄荣金．预设的学习轨迹转化为课堂实践的课例研究——以相等分数为例[J]．数学教育学报，2021，30（3）：25-31．

[27] 赵文君，张晓霞，宁锐，等．课例研究中理论与实践的冲突与融合：活动理论视角[J]．数学教育学报，2021，30（3）：32-37．

[28] 綦春霞，曹辰，张迪．大学与中学数学教师合作促进教师发展的个案研究[J]．数学教育学报，2021，30（3）：38-45．

[29] 伍春兰．PDSA视域下基于教师学习的中学数学课例研修研究[J]．数学教育学报，2021，30（3）：78-82．

Transformative Competencies and Competency Development for 2030 in Junior High School Mathematics Curriculum in China——Curriculum Content Mapping Analysis Based on “OECD Learning Framework 2030”

SUN Xue-min1, TANG Hai-jun1, 2, CAO Yi-ming3

(1. School of Mathematical Science, Guizhou Normal University, Guizhou Guiyang 550025, China;2. College of Mathematics, Sichuan University of Arts and Science, Sichuan Dazhou 635000, China;3. School of Mathematical Science, Beijing Normal University, Beijing 100875, China)

The OECD learning framework 2030 defines three kinds of “Transformative Competencies” that students must have in order to help them cope with the uncertainties of the future world and create a better future. “Competency Development for 2030” is proposed at the same time. This paper is based on the latest research on OECD Education 2030 Project: curriculum content mapping analysis project, which mainly focuses on the development of transformative competencies and competency development for 2030 in mathematics. In this paper, the author makes a deep analysis of the transformative competencies and competency development for 2030 in Chinese mathematics curriculum from the two perspectives of overall distribution and content correlation by using the content analysis, and some enlightenment and suggestions are obtained.

OECD learning framework 2030; mathematics curriculum content mapping; junior high school mathematics curriculum; transformative competencies; competency development for 2030

G632.3

A

1004–9894（2022）06–0045–07

孙学敏，唐海军，曹一鸣．中国初中数学课程中的变革能力与2030能力发展——基于OECD“学习框架2030”的课程图谱分析[J]．数学教育学报，2022，31（6）：45-51．

2022–07–22

教育部基础教育课程教材发展中心、课程教材研究所——课程图谱分析项目；2021年度四川省高校人文社会科学重点研究基地四川教师专业发展研究中心——基于学生作业的实习教师教学反思与教学重建研究（PDTR2021-08）

孙学敏（1987—），女，内蒙古乌兰察布人，博士生，主要从事数学课程与教学论研究．曹一鸣为本文通讯作者．

[责任编校：张楠、陈汉君]