小学数学教师有关学生错误的知识的评价模型构建与应用

张 岳，刘晓玫，Max Stephens，郏超超

小学数学教师有关学生错误的知识的评价模型构建与应用

张 岳1，刘晓玫2，Max Stephens3，郏超超4

（1．北京语言大学 国际学生教育政策与评价研究院，北京 100083；2．首都师范大学 教师教育学院，北京 100037；3．墨尔本大学 教育研究生院，澳大利亚 墨尔本 3010；4．中国基础教育质量监测协同创新中心，北京 100875）

小学数学教师有关学生错误的知识的评价模型为包含内容与认知维度的二维结构．其中，认知维度包括“预测学生错误”“运用数学和课程相关知识识别和描述某个特定数学主题的错误”“分析与阐释学生错误的原因”“处理与纠正学生错误的策略”4个分维度，内容维度以《义务教育数学课程标准（2011年版）》为确立依据，依据模型开发测试工具，通过对来自东、中、西部地区8个省市701名小学数学教师的实测数据进行验证．结果表明：评价模型具有良好的信效度；小学数学教师有关学生错误的知识的整体表现不佳；在认知与内容分维度上表现迥异．

小学数学教师；有关学生错误的知识；评价模型；验证与应用

1 问题提出

教师有关学生错误、误解的理解是其从事教学活动应具备知识的重要组成部分[1]．对学生学习过程中产生的错误进行评估并予以纠正，有助于教师及时调整教学重点和计划，并最终改善学生学业表现[2]．然而，在实际教学中，许多数学教师将学习错误视为教学的阻碍．学生一旦产生错误，教师们最常用的方法是不断地重复标准答案，让学生加强练习，或简单地将学习错误归结为学生粗心大意、上课没有仔细听讲等浅层次的原因[3]．这种肤浅的、武断的行为对学生理解知识、发展能力有害无益，同时也会对学生学习兴趣和自信心造成消极的影响[4]．《义务教育数学课程标准（2011年版）》（以下简称《课程标准》）教学建议中也提出，对于学习有困难的学生，教师应及时给予关注与帮助，鼓励他们积极参与数学学习活动，并尝试以自己的方式解决问题和表达意见和看法；要及时肯定他们的进步，耐心地指导他们分析出现困难或错误的原因，并鼓励他们自我改正，进而增强学习数学的兴趣和信心[5]．因此，对数学教师有关诊断和处理学生在不同的教学情境中学习数学时所犯的错误，意识到错误对数学学习的重要性，知悉错误的原因，并采取有效、及时的教学策略加以纠正的知识，无论对学生学业发展还是对教师专业发展都至关重要．

既有研究对在职数学教师有关学生错误的知识的实证研究较少．国际教育评价项目，如21世纪数学教学研究（Mathematics Teaching in the 21st Century，简称MT21）[6]、数学教师教育与发展（Teacher Education and Development Study in Mathematics，简称TEDS-M）[7]已采用最新测量与评价手段对教师知识进行了测查．但是，其测评对象均为职前数学教师，并没有涉及到更大范围的教师群体．同时，在这些项目中数学教师对学生错误的调查仅是学科教学知识的一个子维度，并未进行深入地挖掘[8-9]．目前，国内研究者提出的有关数学教师诊断学生错误的知识的评价多以某个特定数学主题或诊断学生错误的某个关键环节为研究对象[10-12]，且已有的实证研究多以传统测验方法为依托，难以揭示数学教师有关学生错误知识的潜在认知结构与过程，评价结果解释具有一定的局限性．因此，试图构建小学数学教师有关学生错误的知识的评价模型并进行验证，旨在为教师教育改革、教师专业成长提供实证依据，具体包括如下问题：（1）构建小学数学教师有关学生错误的知识的认知与内容的二维评价模型；（2）据此开发工具，并实施测试并验证；（3）揭示数学教师在总体、认知与内容分维度上的表现与差异状况．

2 评价模型的构建

小学数学教师有关学生错误的知识的评价理论模型包含内容标准、表现标准两个部分．具体而言，内容标准也称为内容细目，是指评价中要求小学数学教师有关学生错误的知识“做什么”的问题．表现标准，也称为表现水平描述，旨在呈现处于不同水平的小学数学教师有关学生错误的知识在内容标准上的掌握程度．内容标准回答评价中期望小学数学教师有关学生错误的知识所要求的知识与技能，而表现标准是对数学教师要达到的程度或水平的界定，是教师有关学生错误的知识“能做什么”的问题．

通常情况下，一项评价任务涉及的内容或知识是具有复杂性的，单维的指标难以满足测评的要求．国际上许多大规模的教育评价项目的框架都是分层的、分类的，由两个或两个以上的维度构成．其中一个维度为评价内容，另一个维度为认知过程，体现评价对象的认知水平或操作的层级．小学数学教师有关学生错误的知识的评价指标体系也采用二维结构，即课程内容的分类和认知过程的分类．

2.1 认知维度

科克斯（Cox）的研究提到，在确定一个错误后，有两个问题是相关的，一是如何系统化地检测出错误？二是一旦错误的模型被识别出来，可以用什么样的方法来弥补这个错误[13]．随着有关数学教师对学生错误行为诊断的研究越来越细化，对学生错误产生的原因做出假设、是否将错误作为课堂教学的重点等指标也被认为是教师处理与分析学生错误的关键步骤．如里科米尼（Riccomini）将对学生错误分析聚集于3个方面：确定教师是否能够识别减法的特定错误模式，确定教师是否能够描述常见的减法错误，确定教师是否能够将这些错误模式作为教学重点[14]．库珀（Cooper）开发了一项培养未来教师分析学生错误的能力，以便使其做出教学决策的课程，包括识别学生错误，对错误可能产生的原因做出假设，然后思考并采取教学策略3个步骤[15]．这是在1988年库尼（Cooney）开发的模型基础上建立起来的．库尼将教学定义为教师收集学生学习的各类信息，分析结果，做出诊断，并在此基础上给予学生回应的互动过程[16]．海因里克斯（Heinrichs）和凯撒（Kaiser）提出，教师分析与诊断学生错误通常包括3个步骤，即感知或识别错误，解释错误，最后对错误进行处理[17]．中国一些一线数学教育工作者从实践的角度提出教学是教师分析学生错误行为的过程．华应龙提出应从如何认识学习错误，分析学习错误及处理学习错误3方面来对待学生错误[18]．吴文娟在此基础上提出，教师对学生错误的诊断过程经历了预设—发现—反馈3个阶段[19]．

数学教师在某个特定数学主题的错误分析上，祖亚（Zuya）选择代数中的变量、代数分式、方程式和文字题为内容，试图解释数学教师能否预测和识别学生思维过程，并提供有用的纠错建议[20]．黄兴丰等人以概念性知识和程度性知识为分析框架，对职前数学教师应对学生概率错误进行调查．结果表明，极少数职前教师可以达到概念性解释学生数学错误的水平，多数教师不能真正解释学生的错误[12]．在教师诊断学生错误的关键环节上，马文杰深入研究了小学数学教师对数学学习错误的矫正原则，并细化为13项[21]．李娜等人基于对初中数学课堂的录像分析将教师反馈学生错误的类型分为陈述型和质疑型[22]．

将上述研究者有关教师对待错误的模型进行归纳提炼发现，教师诊断学生错误的基本过程都包括3个步骤：识别学习错误、寻找错误的原因，以及做出适当的反应．国内外研究者有关数学教师诊断学生错误模型的对比见表1．

此外，专家咨询结果表明，数学教师对学生错误的预判也是其辨析能力的重要组成部分，正如祖亚和吴文娟所言，数学教师应该能够预测学生的典型错误，及时获得学生学习新课前的知识掌握程度的信息．因此，研究将小学数学教师有关学生错误的知识的认知过程分为以下4个阶段．

第一阶段，数学教师对学生错误的预测．这一阶段是后续3个阶段的前提，决定着教师对待学生错误的反应行为．在多数诊断模型中，此阶段并没有涵盖在内．但是，在实际教学中，教师对学生错误的估计往往来源于经验、来源于教材，并非来源于当下所教的学生[19]．所以，学生错误的现状与教师对错误的理解的脱节促使研究将教师对学生错误的预测作为认知过程的第一个阶段．

第二阶段，数学教师运用数学和课程相关知识识别和描述某个特定数学主题的错误．只有当一个错误被感知的时候，教师才可能对其做出反应．在上述提到的模型中，这一阶段常常作为教师诊断学生错误的第一个阶段．可见，此阶段是教师对学生错误进行原因分析与处理的基础环节．

第三阶段，数学教师对错误的原因进行假设、分析与阐释．这个阶段基本可以在前文提到的所有诊断过程模型中找到．为了能够识别错误的根源在哪，教师们需要对造成错误的原因做出恰当的假设，并在此基础上深入分析，这对纠正学生的错误至关重要．

第四阶段，数学教师在对前3个阶段的认识与分析基础上，找到解决学生错误的教学方法，并处理与矫正学生的错误．已有研究也显示，教师必须处理错误，以培养和纠正学生的理解力，才能最终达成教学目标．

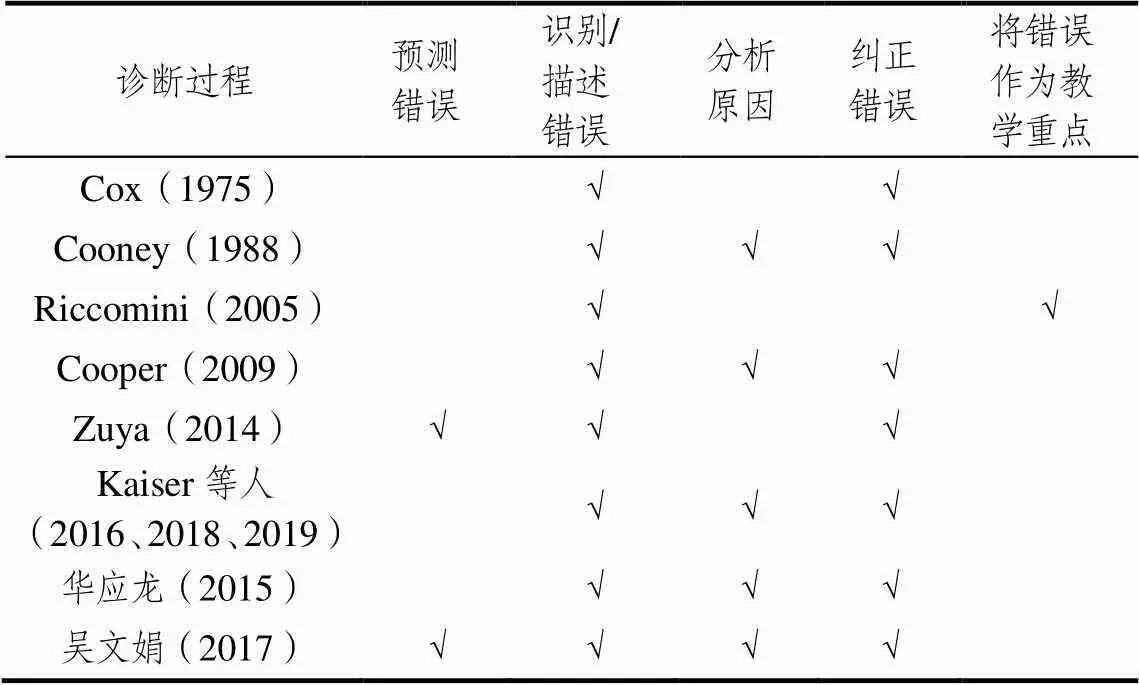
表1 有关数学教师诊断学生错误模型的对比

2.2 内容维度

在建立小学数学教师有关学生错误的知识的认知过程维度基础上，需要考虑的另一个维度就是在不同的数学内容领域数学教师有关学生错误的知识．《课程标准》是国家对学生学业发展的总体目标和要求，是教材编写、教师教学的基本依据，集中体现了教育目标，自然为教师知识的评价提供了基本框架，即《课程标准》所要求掌握的知识和能力应作为小学数学教师有关学生错误的知识的内容维度的重要依据和现实选择．据此建构评价模型，如图1．

3 研究设计

3.1 研究方法

参照国际教育评价项目的整体设计思路，结合专家咨询法和访谈法构建小学数学教师有关学生错误的知识的评价模型，并据此开发测试工具，采用测量研究法进行实测．

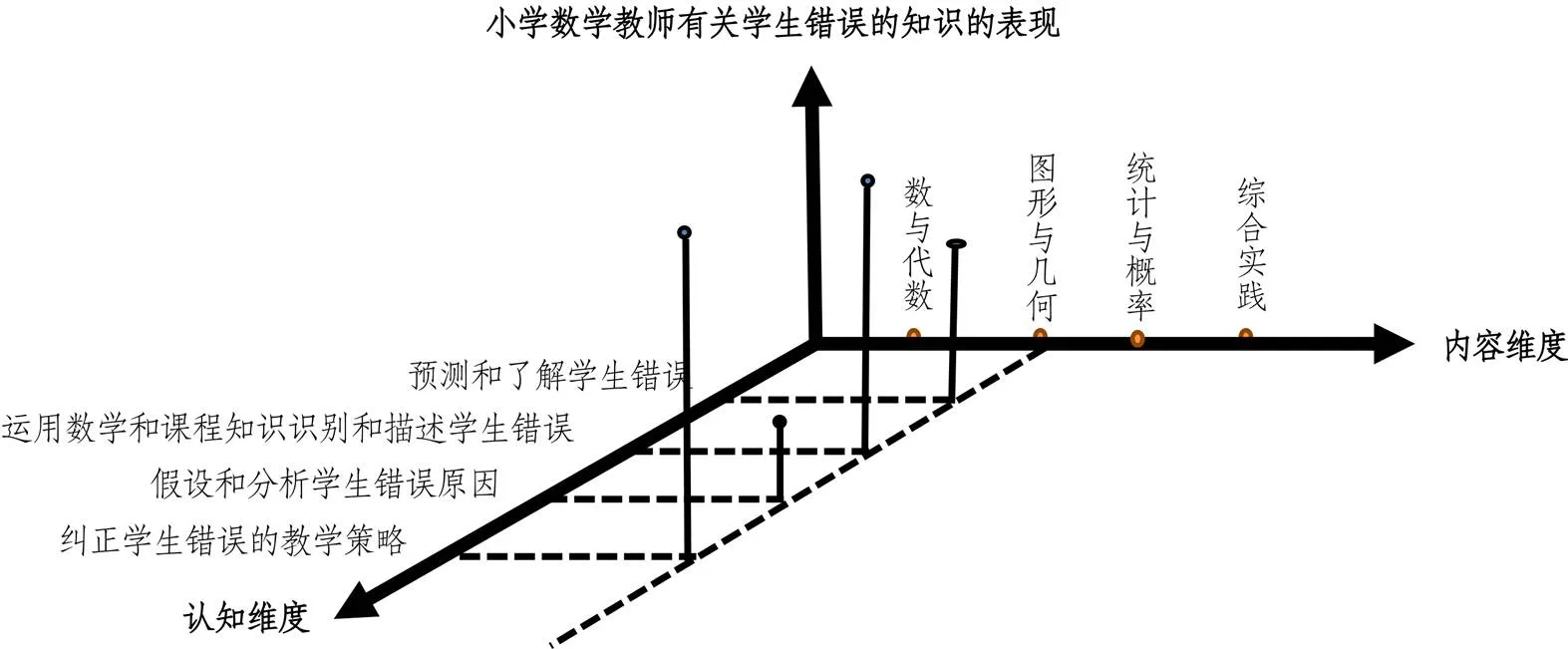
图1 小学数学教师有关学生错误的知识的评价模型

3.2 研究对象

参与模型修订与确立的咨询专家包括墨尔本大学、迪肯大学、北京师范大学、华东师范大学、首都师范大学、南京师范大学、北京教育学院等国内外高校数学教育领域、教育测量领域的学者，以及北京、浙江、安徽、陕西和广西等地区的教研员及一线教师，共计32名．实施测试后，参与结果访谈的专家包括来自北京、浙江的数学教育专家、一线教师和教研员，共计12名．

参与模型验证的小学数学教师样本来自东、中、西部地区，共计8个省（市）．考虑学校所在地理位置等因素，在每个省随机选取区县，按照城市、县镇、乡镇和农村4个类别进行抽样，在每个类别中抽取60名四～六年级的数学教师，共计720名教师．抽取教师的平均年龄为38岁，教授数学学科的平均教龄为15年．样本分布情况见表2．

3.3 数据收集与处理

正式测试在各地教育行政部门或教研员的统一安排下进行．问卷回收后，对测试卷的异常作答，如抄袭、随机作答等进行处理与删除．共发放问卷720份，剔除测试卷的异常作答，如抄袭、随机作答等，回收有效问卷701份，有效率为97%．

采用验证性因子分析对评价模型进行验证，通过项目反应理论对教师表现进行估计．数据处理与分析采用SPSS22.0、Mplus7.0、ConQuest软件完成．

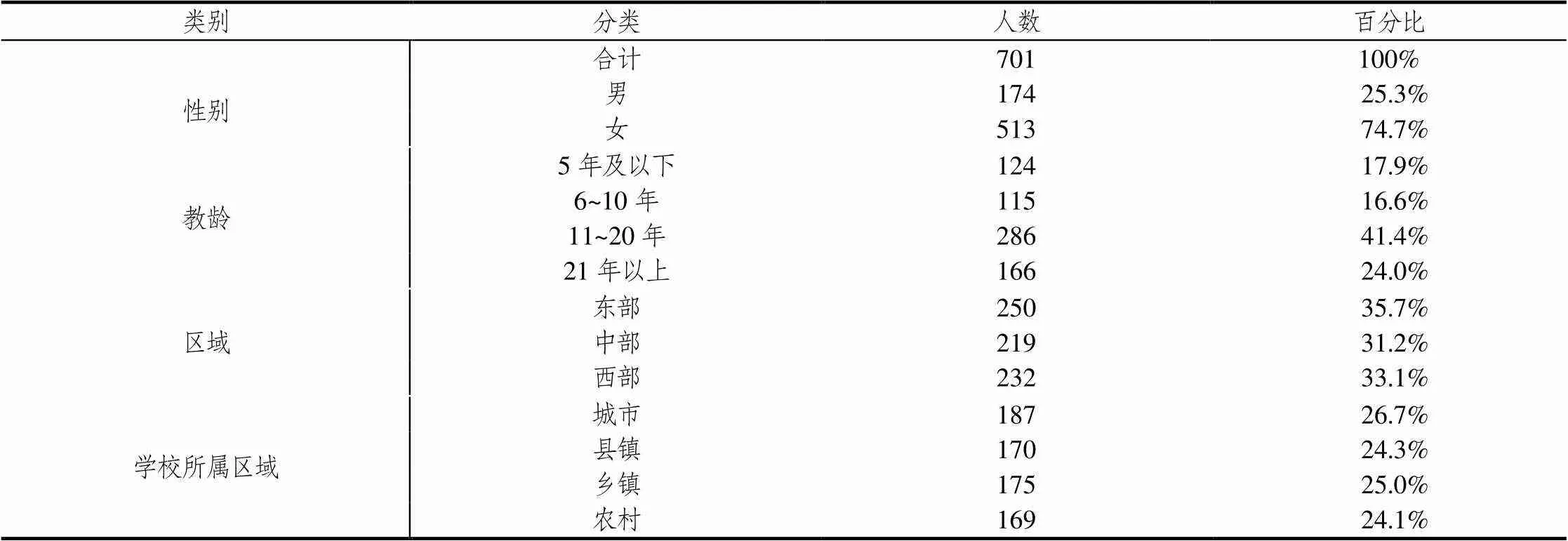
表2 小学数学教师各类别变量的分布情况

注：因教师在性别、教龄上的填答有缺失，故在这两个变量的人数加总小于总人数．但因不涉及针对性别、教龄的数据分析，所以并不影响分数估计、验证性因子分析结果的科学性．

4 评价模型的构建及应用

4.1 测试工具的开发

选取四年级“图形与几何”课程内容开发测试工具．

选择四年级的主要原因如下：皮亚杰认知发展理论提出，7～11岁儿童处于具体运算阶段．在这个阶段，儿童已迅速获得认知操作能力，并能运用这些新的技能思考事物，可以很好地理解数量关系和逻辑关系．在数学概念发展上，9～11岁的儿童处于认识形状、水平和垂直坐标及面积概念的阶段．再者，根据《课程标准》对学段的划分，四年级是小学高年级的开始，对学生学习数学起着承前启后的作用．最后，无论是国际大规模教育评价项目，如TIMSS、NAEP等，还是中国义务教育质量监测，均认为四年级是学生个体能力水平发展的关键阶段[23]．

选择“图形与几何”作为工具研发的内容维度的原因主要包括两个方面：就内容本身而言，几何初步知识是小学数学基础知识的重要组成部分，是数学中最直观、最具体的一部分，并且与现实生活联系紧密，同时也是将来小学高年级和初中阶段学习的必备基础．此外，几何知识不是独立的，而是环环相扣的，是一个系统化的整体．如果学生在发展的关键阶段没有打好几何学习的基础，会影响后续几何知识，乃至整个数学学习的效果．另外，中国从2001年课程改革开始，几何课程的内容变得更加丰富，教师作为课程知识的实施者，其几何知识的教学能力也面临较大的挑战．就“图形与几何”的教学现状而言，许多研究指出，学生在识别几何形状、解决空间推理问题的过程中存在困难[24]．同样地，数学专业的师范生和有经验的教师与学生一样，对几何知识也存在相同的误解[25]．因为测试年级和几何学习的重要性等因素，根据《课程标准》对四年级“图形与几何”课程内容的规定，将内容维度进一步细化为图形的认识、测量、图形的运动、图形与位置4个子维度．

小学数学教师有关学生错误的知识的测试题目在北京、安徽和广西三地进行两轮预试，同时通过多群体、多地域、多轮次的咨询与访谈，专家在如下方面达成一致：在评价目的与定位方面，绝大多数专家赞同测试的目的在于获得教师对四年级学生“图形与几何”基础知识的掌握程度的信息，而非通过本次测试鉴别学生在该内容维度上的水平．专家们普遍认为基础知识的掌握奠定学生未来学习的基础，对教师针对学生掌握基础知识时常见错误的辨析的评价更有利于从源头帮助学习有困难的学生消除误解，矫正错误．在题目难度方面，有关学生错误的知识侧重于教师对学生掌握基础知识的程度进行判断与分析，学生在难度较小的题目上映射出的典型错误是研究的关注点．在题目的表述和形式方面，对部分题目的语言表述、设问方式等进行规范化修改，使测试题更贴近小学数学教育的实际．

最终测试题目确定为主观建构题，共10道大题，38个小题，测试时间为不限时．为了避免主观建构题太多导致测试卷过长，引起参测教师作答疲劳进而降低回收质量，研究采用循环铆的题本设计．将所有的测试题目根据评价模型的维度进行组块，然后将组块循环放入不同的题本中，两两题本之间有两道大题为共同题，最终组成5个题本．

4.2 评价模型的验证

研究采用项目反应理论对测试题目进行估计．结果表明，测试题区分度在0.25～0.73之间，难度在0.01～0.64之间，IRT难度在-2.43～2.63之间．题本1至题本5的内部一致性系数分别为0.74、0.80、0.74、0.78和0.77，满足良好测验对题目的基本要求．同时，评价模型的验证性因子分析结果为：2=155.15，=2，=0.09，=0.96，=0.93，这表明模型的拟合良好，结构效度符合测量学要求．因子分析结果见图2．

同时，专家认同测试卷中数学主题为四年级学生日常学习“图形与几何”基础知识时常犯的学习错误，保证了题目的内容效度．

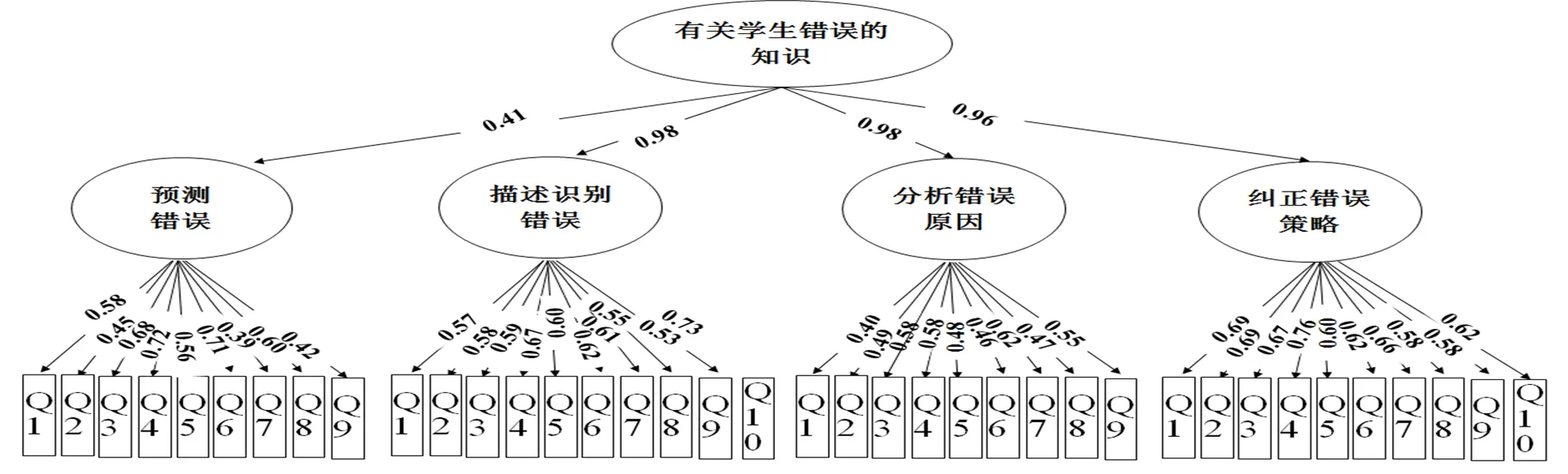
图2 小学数学教师有关学生错误的知识的评价模型的验证性因子分析结果

4.3 表现标准的编制

为了便于对测试结果进行报告与解释，往往需要根据相应的表现标准描述将评价对象划分到有序的表现水平中去．科学的、可操作性的表现标准是衡量与解释小学数学教师有关学生错误的知识的重要依据．表现标准的制订具体可分为以下4个步骤．

第一，依据评价指标体系的二维结构，结合两轮预试的数学教师的作答结果，制订表现标准初稿；

第二，正式测试后，在各题本中抽取约10%的问卷进行预评，根据预评结果，对表现标准进行相应的修订；

第三，将选取出的典型样题及表现标准发给专家进行审核与评分，根据审核意见进行修订并最终确定表现标准；

第四，为了更好地对数学教师的分数做出解释，说明达到某个分数的教师能够做什么．对小学数学教师有关学生错误的作答反应采用分步计分模型进行分数估计，对数学教师在认知和内容维度上的表现分别采用多维Rasch模型进行估计．

在IRT标准分数基础上，对其进行线性转换，将小学数学教师有关学生错误的知识的总体表现转换为均值为500分，标准差为100分的量尺分数；对于内容或认知维度，以其中表现最弱的一个子维度为基准进行标准化，再进行线性转换为均值为200分，标准差为50分的量尺分数，从而使内容和认知维度各子维度之间具有可比性．

研究中，小学数学教师预测和了解学生错误子维度赋值0～1分，依据学生测试卷得到的正确作答率，教师能够准确预测学生正确作答率所在范围计为1分，否则计为0分．小学数学教师有关学科和课程知识的理解、有关学生错误的原因分析、针对学习错误的教学策略3个子维度赋值0～2分．采用反应类别组合方法（参照TIMSS对问卷量表划分区域的反应类别组合方法来确定教师表现的不同水平）来确定小学数学教师原始分数的切分点．因为Rasch量尺的特点是每个原始分数都对应一个量尺分数，把小学数学教师得到的原始分数的切分点与量尺分数进行对应，可以将数学教师有关学生错误的知识划分为3个等级，分别为初等水平、中等水平、优等水平，具体描述见表3．为了更直观地呈现小学数学教师有关学生错误的表现水平，以“图形的运动”子维度的样题为例进行说明，见表4．

4.4 实测结果

第一，小学数学教师有关学生错误的知识的整体表现不佳，多数数学教师仍处于中等偏下的水平，仅有15.0%的数学教师可以达到优等水平．这一结论在一定程度上验证了以往研究关于数学教师辨析错误能力的研究结果．

第二，在内容维度上，小学数学教师在“图形的认识”子维度上表现最差，量尺分数为200分，达到优等水平的教师比例为12.0%；在“测量”子维度上表现最好，量尺分数为250分，达到优等水平的教师比例为47.0%．

第三，在认知维度上，小学数学教师在“分析学生错误的原因”子维度上表现最差，量尺分数为200分，达到优等水平的教师比例为3.4%；在“运用数学和课程知识描述学生错误”子维度表现最好，量尺分数为343分，达到优等水平的教师比例为52.9%．具体结果见表5．

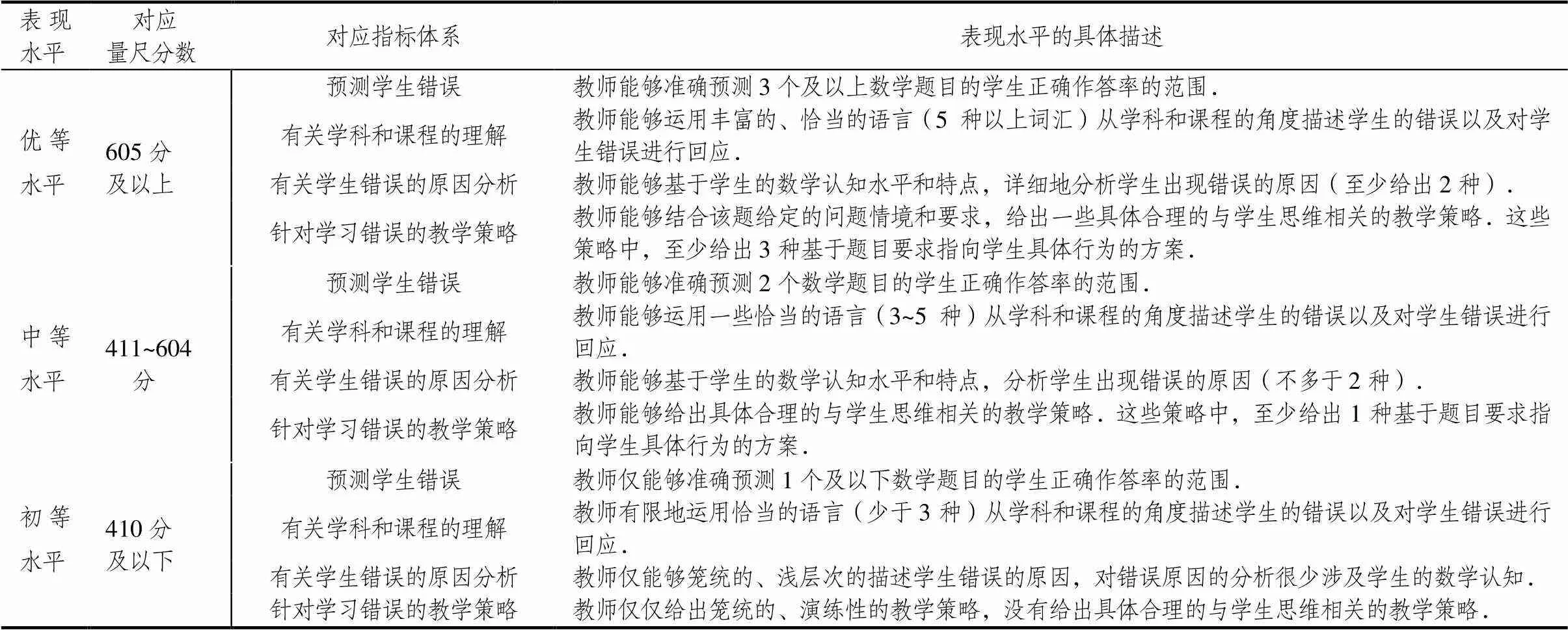
表3 小学数学教师有关学生错误的知识的表现标准描述

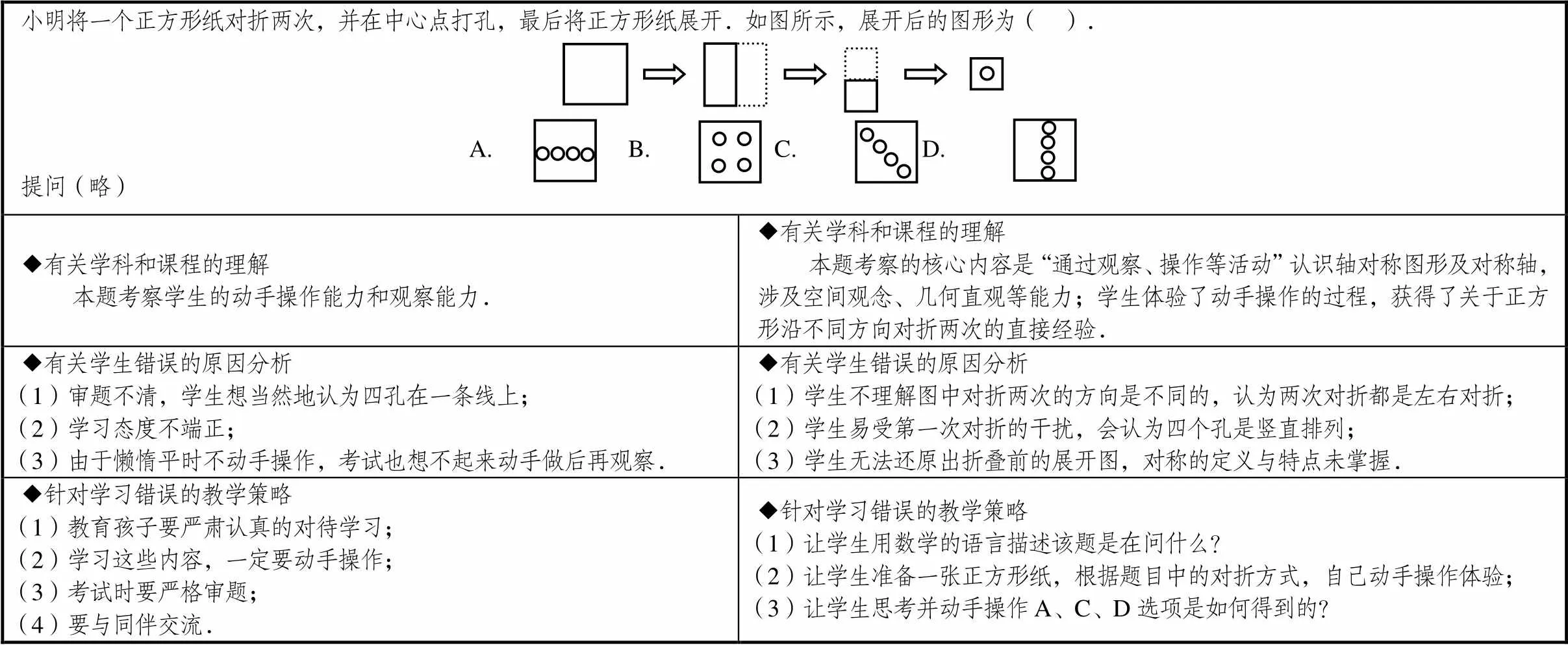
表4 小学数学教师在“图形的运动”子维度的样题及典型作答

表5 小学数学教师有关学生错误的知识内容和认知维度的量尺分数与表现水平

5 分析与讨论

小学数学教师在“图形的认识”和“测量”子维度上存在差异，其原因可能在于课程内容本身的属性以及长久以来中国几何教学中存在的历史问题．首先，《课程标准》中“图形与几何”课程内容属性的不同，在一定程度上导致了数学教师在不同内容子维度上表现的差异．测量的内容与解决问题的方法相关较高，学生容易从抽象的问题中找到解题方法，所以学生易犯错误的地方与相应的教师纠错方法也相对明确．从学段上看，四年级学生在测量上只学习了二维图形，如长方形与正方形面积和周长的计算方法，需要解决的度量问题较少，且图形的种类单一．而图形的认识的内容涉及有关图形的要素之间、图形的本质、关系与特征的内容，一些教师自身对这方面的知识存在认知盲区，受到自身能力的限制，他们在讲课时采用的教学设计与方法也存在一定的偏差，课后又不能及时地发现学生错误的本质，纠错的策略也就不成熟，不具有针对性．吴卫东等人的研究表明，小学数学教师的新课程教学的内容知识，即关于数学概念和过程的知识急待提高[26]．尹瑶芳也提出，小学数学教师对坐标几何、度量几何和画法几何总体掌握较好，变换几何、直观几何和演绎几何知识较为欠缺．同时，访谈结果也发现，数学教师对新课标几何内容宽度广度认识不足，受教育观和知识观的限制，部分教师易出现数学思维稚化现象[27]．再有，长久以来，中国小学几何教学侧重于计算几何．在教学中，许多老师往往在教授几何知识的时候仍然重视计算的过程，忽略对图形的要素、关系与特征的研究．这一历史遗留问题至今仍然影响着中国小学几何教学．教师在知识、观念上的固化致使在教学行为上的缺失，进而导致他们在学生发生有关图形的认识的错误时难以跟进与分析．

小学数学教师在“分析学生错误的原因”子维度上的不良表现可能与小学数学教师关于学生心理发展特征与认知过程的知识储备不足有关．已有文献研究表明，职前数学教师判断学生反应原因的能力是相对匮乏的．具体到对学生错误原因的分析，数学教师常常过于泛化地、片面地对错误进行归因[28]．学生已有的知识经验包含但不限于他们的知识、技能基础、学习、生活经验，是实施有效教学的前提条件，对学生知识现状、困难的掌握与分析应该成为教学的起点．然而教师想要读懂学生并非易事．学习数学知识、掌握某种教学技能与方法是相对容易的；洞悉学生深层次的认知、心理变化与特点是困难的，也是漫长的．从时间成本与结果来看，数学教师教学技能的提升对学生学业成绩的影响是高效的、显性的；而花时间关注学生思维，读懂学生的工作是隐性的，很难量化对学生的成长产生了多大程度的影响．这可能是多数小学数学教师面对学生错误“不为”的原因．张晓贵对比两岸三地数学教育课程设置发现，数学学习的知识包括数学思维、数学学习的错误分析、数学学习的情意因素以及学习理论等．与中国台湾、中国香港相比，中国内地数学学科教学论中虽然包含学生数学学习知识，但和数学课程的知识类似，所提供的数学学习知识是不充分的，缺少学生数学学习心理学和社会学分析的必要内容[29]．从中国数学教师教育课程设置来看，有关儿童心理发展、认知特点的课程仍处在边缘地位，虽然学校在课程安排中有心理学相关课程，但学生普遍认为心理学与中文、英语等公共课一样，不如专业必修课重要[30]．曾小平等人提出，中国高师院校本科小学教育专业建设存在缺乏对儿童学习心理的深入研究．小学教育专业（数学方向）的核心课程应包括让教师初步了解数学学习心理的基本理论，了解小学生数学认知发展概况，了解小学生数学思维的发展概况，了解数学教育心理研究的基本方法的内容[31]．越来越多的研究者建议小学数学教育专业课程中应增加数学学习心理学、教育学和数学相结合的课程[32]．数学教师在职前教育阶段有关学生心理与认知发展的知识相对匮乏，导致了他们在今后教学中对学生思维认知关注的缺位，这也是小学数学教师面对学生错误的“难为”之处．

小学数学教师在“运用数学和课程知识描述学生错误”子维度上的良好表现可能与数学教师参与培训、日常研讨的内容有关．近年来，研究者改进研究设计与方法后对教师培训与学生学业成绩关系的研究结果表明，教师参与培训对小学生数学成绩有显著的正向影响．希尔（Hill）等人发现，以数学内容为中心的职前培训和专业发展活动对数学教师如何设计教学、如何处理学生困惑很重要，并对提高学生数学成绩有积极的作用[33]．陈向明等人基于11个省（直辖市），涉及东中西不同经济发展地区，兼顾城乡及不同层次学校类型的教师培训调查结果发现，教育教学理论、学科教学是教师们接受最多的两种培训内容[34]．可见，数学教师最常参加涉及有关数学学科知识的内容的培训，对他们把握数学课程知识有较大帮助．

6 结论与建议

6.1 结论

（1）小学数学教师有关学生错误的知识可以用包括认知维度和内容维度的二维评价模型进行有效评价．该模型突破了传统测验理论的局限性，对有关学生错误的知识的核心组成部分进行了全面系统的分析与论证，在一定程度上丰富了数学教师学科教学知识的研究．

（2）以小学数学教师有关学生错误的知识的二维评价模型为蓝图，结合专家咨询、个别访谈等方法开发的测评工具信效度良好，可操作性强；验证性因子分析的结果证明此模型拟合良好，结构稳定可靠，构建模型的方法选择恰当且高效．小学数学教师有关学生错误的知识的评价在教育测量最新技术与方法指导下进行测试，提供了小学数学教师更为精细化的、潜在的对学生错误的认知过程与特质，可为教育决策、教学改进、学生发展提供可靠的数据支撑与参考依据．

调查没有涉及四年级以外的其它年级和《课程标准》中小学数学的其它内容维度，一定程度上限制了评价框架的推广性与普适性．受限于研究样本、题本设计、作答时间等客观条件，研究仅开发了四年级“图形与几何”内容上的测试工具对有关学生错误的知识的评价指标进行操作化的测试与验证．对于小学其它年级，以及数学教师有关学生错误的知识的评价框架在“数与代数”“统计与概率”内容上的适用性还有待进一步分析．未来的研究可以考虑将影响小学数学教师有关学生错误的知识的相关因素纳入评价框架中，可为改进教师教学行为提供更具针对性的指导意见．

（3）多数小学数学教师处理学生错误时表现欠佳，这一现状应引起足够的重视．调查结果表明，85.0%的小学数学教师对学生错误的了解与预测、识别与描述、诊断与阐释、纠正与处理的相关知识处在初等或中等水平，整体表现并不理想，亟需提高．同时，各子维度之间差异较大，尤其是认知子维度．小学数学教师在“运用数学和课程知识描述学生错误”“纠正学生错误的教学策略”“预测学生错误”子维度上的量尺分数均在300分以上，远高于“分析学生错误的原因”子维度；在达到优等水平的教师比例上分布稍有不同，约45.0%以上的教师在“运用数学和课程知识描述学生错误”“纠正学生错误的教学策略”子维度上可以达到优等水平，但仅有不足10.0%的教师在“预测学生错误”“分析学生错误的原因”子维度上可以达到优等水平．

（4）小学数学教师职前培养阶段的课程设置、有关学生错误分析与处理相关研讨与培训的缺失，以及内在知识结构、观念的固化等多重原因，导致其在分析学生错误时表现不佳．

6.2 建议

（1）在教师职前和职后教育中，注重从学生本位理念出发，适当增加有关对学生认知研究的心理学等相关课程的比重，从源头上弥补教师有关学生知识的缺失．相比于传统的、高高在上的纯理论性培训，有关学生错误的培训主题更贴近教师们的教学实践，容易引起共鸣，每位教师对学生错误都可以基于自己的实际教学各抒己见、畅所欲言．建议各级教育部门合理设计有关学生错误的知识的培训方案，为不同地域的数学教师提供多元化、个性化的指导与支持．

（2）随着新课程理念的发展、倡导自主探索与建构的数学教学、以学生为本的教学信念，越来越多的教师认识到学生错误的积极价值，认识到学生的错误可能蕴含着比正确答案更丰富的信息，对这些信息的辨别与分析可能成为学生发展新的增长点．由于时间的限制、教学效果的时效性、自身能力等原因，数学教师在分析学生错误原因中面临着“不为”与“难为”困境．建议数学教师在面对学生的错误时，应积极转变固有的关注知识的教学观，树立为学生服务的意识，放慢脚步，避免急功近利，学会读懂学生．

[1] Shulman L S. Those who understand: Knowledge growth in teaching [J]. Educational Researcher, 1986, 15 (2): 4-14.

[2] Salvia J, Hughes C. Curriculum-based assessment: Testing what is taught [M]. New York: Macmillan, 1990: 365.

[3] Clements M A. Careless errors made by sixth-grade students on written mathematical tasks [J]. Journal of Research in Mathematics Education, 1982, 13 (2):136-144.

[4] Fuchs L S, Fuchs D, Hamlett C L. Strengthening the connection between assessment and instructional planning with expert systems [J]. Exceptional Children, 1994, 61 (2): 138-146.

[5] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012：49．

[6] William H S, Maria T T, Kiril B. The preparation gap: Teacher education for middle school mathematics in six countries----MT21 report [R]. MSU Center for Research in Mathematics and Science Education, Michigan State University, 2007: 2-10.

[7] Tatto M T, Schwille J, Senk S, et al. Teacher education and development study in mathematics (TEDS-M): Policy, practice, and readiness to teach primary and secondary mathematics conceptual framework [R]. Teacher Education and Development International Study Center, College of Education, Michigan State University, 2008: 13-14.

[8] 邵珍红，曹一鸣．数学教学知识测试工具简介及其相关应用[J]．数学教育学报，2014，23（2）：40-44．

[9] 李琼，倪玉菁，萧宁波．小学数学教师的学科知识：表现特点及其关系研究[J]．教育学报，2006（12）：58-59．

[10] 孙兴华，马云鹏．小学数学教师如何处理学生计算错误的研究——以两位数乘两位数为例[J]．数学教育学报，2016，25（5）：38-44.

[11] 陈建华，文清．数学教师纠错教学策略研究——从处理学生解题错误谈起[J]．教育与教学研究，2014，28（6）：49-53．

[12] 黄兴丰，马云鹏．职前数学教师如何应对学生的概率错误[J]．数学教育学报，2015，24（3）：28-34．

[13] Cox L. Diagnosing and remediating systematic errors in addition and subtraction computations [J]. The Arithmetic Teacher, 1975, 22 (2): 151-157.

[14] Riccomini P J. Identification and remediation of systematic error patterns in subtraction [J]. Learning Disability Quarterly, 2005, 28 (3): 233-242.

[15] Cooper S. Preservice teachers’ analysis of children’s work to make instructional decisions [J]. School Science and Mathematics, 2009, 109 (6): 355-362.

[16] Cooney T J. Teachers’ decision making [M] // Pim D. Mathematics, teachers and children. London: Hodder and Stoughton in Association with the Open University, 1988: 91.

[17] Heinrichs H, Kaiser G. Diagnostic competence for dealing with students’ errors-fostering diagnostic competence in error situations [M] // Leuders T, Philipp K, Leuders J. Diagnostic competence of mathematics teachers. New York: Springer, 2018: 79-94.

[18] 华应龙．错若化开，成长自来[J]．人民教育，2017（20）：77-79．

[19] 吴文娟．化错：从诊断学生的真实错误开始[J]．江苏教育研究，2017（11）：40-43．

[20] Zuya H E. Mathematics teachers’ responses to students’ misconception in algebra [J]. International Journal of Research in Education Methodology, 2014 (9): 830-836.

[21] 马文杰．反思与“重构”数学学习错误矫正原则[J]．数学教育学报，2020，29（4）：11-17．

[22] 李娜，莫雅慈，吴立宝．初中数学课堂中教师对学生错误反馈的类型研究——基于24节录像课的分析[J]．数学教育学报，2016，25（5）：55-60．

[23] 辛涛，李峰，李凌艳．基础教育质量监测的国际比较[J]．北京师范大学学报（社会科学版），2007（6）：5-10．

[24] Elia I, Gagatsis A. Young children’s understanding of geometric shapes: The role of geometric models [J]. European Early Childhood Education Research, 2003, 11 (2): 43-61.

[25] Wang S, Kinzel M. How do they know it is a parallelogram? Analyzing geometric discourse at van Hield level 3 [J]. Research in Mathematics Education, 2014, 16 (3): 288-305.

[26] 吴卫东，彭文波，郑丹丹，等．小学教师教学知识现状及其影响因素的调查研究[J]．教师教育研究，2005（4）：59-64．

[27] 尹瑶芳．小学数学教师图形与几何知识状况调查——以上海市浦东新区为例[J]．数学教育学报，2020，29（5）：46-51．

[28] Even R, Markovitz Z. Some aspects of teachers’ and students’ views on student reasoning and knowledge construction [J]. International Journal of Mathematics Education in Science Technology, 1995 (26): 531-544.

[29] 张晓贵．两岸三地数学教师教育中数学教育类课程设置的比较[J]．数学教育学报，2009，18（1）：63-66．

[30] 卢永翠，张廷艳．“国考”背景下数学师范专业课程设置的调查与思考[J]．教师教育学报，2019，6（1）：57-65．

[31] 曾小平，郜舒竹，王智秋．试论高师本科小学教育专业的核心课程——以数学方向为例[J]．数学教育学报，2011，20（6）：68-73．

[32] 徐建星．小学教育专业数学教育类课程的构建——基于MKT的视角[J]．数学教育学报，2017，26（5）：54-58．

[33] Hill H C, Rowan B, Ball D L. Effects of teachers’ mathematical knowledge for teaching on student achievement [J]. American Educational Research Journal, 2005, 42 (2): 371-406.

[34] 陈向明，王志明．义务教育阶段教师培训调查：现状、问题与建议[J]．开放教育研究，2013，19（4）：11-19．

Study on Construction and Application of Assessment Model of Primary School Mathematics Teachers’ Knowledge about Students’ Misconceptions

ZHANG Yue1, LIU Xiao-mei2, Max Stephens3, JIA Chao-chao4

(1. Institute on Educational Policy and Evaluation of International Students, Beijing Language and Culture University, Beijing 100083, China;2. College of Teacher Education, Capital Normal University, Beijing 100037, China;3. Graduate School of Education, The University of Melbourne, Melbourne 3010, Australia;4. Collaborative Innovation Center of Assessment toward Basic Education Quality, Beijing 100875, China)

The assessment model of primary school mathematics teachers’ knowledge about students’ misconceptions based on cognitive diagnostic assessment approach is a two-dimensional structure including cognition and content category. The cognition category includes four sub-categories, which were predicting the students’ misconceptions, using mathematics and curriculum- related knowledge to identify and describe errors on a specific mathematical topic, analyzing and explaining the reasons for students’ misconceptions, and strategies for dealing with and correcting students’ misconceptions. The content category is developed based on. Interview and counseling method are used in construction and modification of model and developing the test tools. 701 primary school mathematics teachers from 8 provinces and cities in east, central and west of China are tested to verify the assessment model. The results show that the assessment model has good reliability and validity. On the whole, the performance of mathematics teachers’ knowledge about students’ misconceptions should be improved, and the performance of cognitive and content sub-categories is very different.

primary school mathematics teachers; knowledge about students’ misconceptions; assessment model; verification and application

G622

A

1004–9894（2022）06–0030–08

张岳，刘晓玫，Max Stephens，等．小学数学教师有关学生错误的知识的评价模型构建与应用[J]．数学教育学报，2022，31（6）：30-37．

2022–05–20

北京市教育科学“十四五”规划2021年度青年专项课题——首都高校来华留学本科生汉语学习质量评价体系研究（CDCA21116）

张岳（1984—），女，山西阳泉人，助理研究员，博士，主要从事学科教育与教师专业发展、教育测量与评价研究．刘晓玫为本文通讯作者．

[责任编校：陈隽、陈汉君]