SF6气体绝缘设备局部放电分解特征组分三角形诊断法
2022-12-27李予全吴司颖董曼玲姚德贵寇晓适曾福平
李予全,吴司颖,董曼玲,姚德贵,寇晓适,王 伟,唐 炬,曾福平
(1. 国网河南省电力有限公司电力科学研究院,河南 郑州 450052;2. 国网江苏省电力有限公司超高压分公司,江苏 南京 211100;3. 武汉大学 电气与自动化学院,湖北 武汉 430072)
0 引言
以全封闭式组合电器(GIS)等为代表的SF6气体绝缘设备(GIE)自1967年在德国首次投运以来,因其占地面积小、可靠性高、配置灵活等优点[1]在电力系统中有着广泛的应用,目前GIS 以六氟化硫(SF6)作为主要的灭弧和绝缘介质。SF6在常温常压下是一种无色、无味、无毒、不燃的气体,具有很好的稳定性、优良的绝缘和灭弧性能[2]。SF6气体绝缘设备虽然比普通的电气设备更可靠,但仍然具有很高的故障率,因此十分有必要对其进行可靠全面的故障诊断。GIS 故障主要分为放电性故障[3]和过热性故障[4],对于放电性故障可分为局部放电、火花放电和电弧放电,其中局部放电(partial discharge,PD)最为常见[5]。目前针对GIS 的PD 主要采用电测法、超声法和特高频法等[6]进行检测,但是电测法和超声法容易受现场测量时电磁噪声和高频振动的干扰,而特高频法存在不能对放电进行定量分析的缺点[7]。因此,建立一种不受电磁干扰并且具有定量分析能力的检测方法十分必要。
针对变压器内部故障,基于油中溶解气体分析的诊断方法已经发展较为成熟[10-11]。其中,由Mi‐chel Duval 提出的大卫三角形故障诊断法[12]是基于3种烃类气体(CH4、C2H4、C2H2)的体积分数进行的故障类型诊断,是IEC 60599:2015[13]标准推荐的故障诊断方法。对于气体绝缘设备,可以类似地将SF6故障分解的特征气体组分作为三角形坐标轴的三边,建立GIS 设备故障诊断方法[14]。目前建立的SF6分解成分分析方法主要基于浓度比[15]和计算机识别算法[16],例如支持向量机和模糊C 均值聚类算法(FCM)。然而,它们并不总是通用的或不适用于电力生产的现场维护,并且不能直观地判断故障所属类型。为此,本文针对局部放电(PD)的主要类型(包括金属突出物缺陷、自由金属微粒缺陷、绝缘子污秽缺陷和绝缘子气隙缺陷[17]),建立PD类型-三角形故障诊断方法,并使用高斯混合模型(Gaussian mixture model,GMM)对三角形故障诊断方法进行改进。
1 建立三角形故障诊断方法
1.1 PD分解特性及组分含量占比分析
SF6在设备内部出现PD 等绝缘故障时会发生分解,可能生成CF4、CO2、SO2F2、SOF2、SO2、SOF4、HF和H2S等产物[18],这些分解组分存在以下特点:
(1)CF4、CO2、SO2F2、SOF2、SO2这5种特征组分含量稳定,易于检测。
(2)SOF4极易水解,其含量受设备内水分含量的影响很大。
(3)HF化学特性非常活泼,极易与设备中水分、金属、绝缘材料等发生化学反应,并且HF 难于检测,无法使用GC 以及GC/MS 检测仪进行定量检测。
(4)H2S的化学性质稳定,但PD后检测到的H2S含量极少,实验中难以通过GC/MS 检测仪检测出,因此本文暂不考虑将H2S作为故障诊断特征量。
考虑到以上几点原因和不同故障数据量的全面性,本文研究故障诊断方法时主要针对CF4、CO2、SO2F2、SOF2和SO2这5种特征分解气体。其中CO2和CF4为含碳特征气体,C 原子主要来源于有机固体绝缘材料和设备内部的含碳金属材料表面,不仅能表征故障位置是否涉及有机固体绝缘材料,还能表征故障涉及有机固体绝缘材料的劣化程度,因此考虑将CO2+CF4作为一个备选特征量。另外,SO2主要由SOF2生成,两者都为稳定的产物,因此考虑将SO2+SOF2作为一个备选特征量。
(笔者译:诞生在这一环境下的萨卢塔蒂的哲学理念,也就必然与传统的三段论式的推理方法相去甚远。尽管同样是接受了苏格拉底、天主教以及圣方济各等人的理论,但这一新的哲学流派只是将传统的理论和哲学家当成转达真理的途径,其目的是在其中寻找到自己需要的内容。而与亚里士多德和托马斯·阿奎那主义的哲学理念相比,方济各流派的哲学更加贴近萨卢塔蒂的“意志至上”论,因为后者能够为其提供更多的支持。而前者甚至威胁到了天主教理论中最宝贵的部分。)
GIS 内部4种典型绝缘缺陷(金属突出物缺陷(N 类)、自由金属微粒缺陷(P 类)、绝缘子表面污秽缺陷(M 类)、绝缘子表面气隙缺陷(G 类))下的PD分解特性如图1 所示[19]。由故障96 h 时不同程度PD下5种气体的体积分数示意图可以看出:
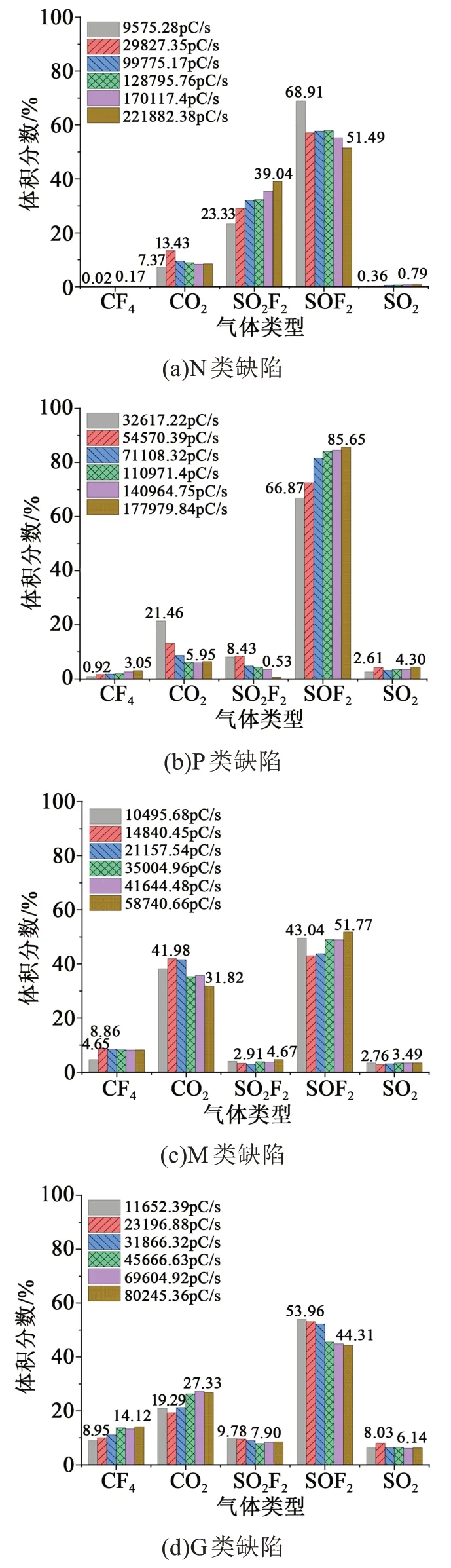
图1 故障96 h不同程度PD下5种气体体积分数比示意图Fig.1 Volume fraction of five gases at different levels of PD at fault for 96 h
(1)当设备发生PD 故障类型时,5种组分中SOF2的含量占比最大。尤其是P 类缺陷下,SOF2体积分数最高值达到85.65%,此时放电量最大,且在P类缺陷下SOF2含量随着放电量的增加而增大。4种缺陷类型下SOF2含量从大到小依次为P 类缺陷、N类缺陷、G 类缺陷、M 类缺陷,P 类缺陷下SOF2体积分数的最小值为66.87%,而N 类缺陷下除了放电量为9575.28 pC/s 这一组的SOF2体积分数达到68.91%之外,其余均为60%以下,N 类缺陷下SOF2的含量普遍高于M类缺陷和G类缺陷,因此SOF2含量可以用来辨别GIE 内部N 类缺陷、P 类缺陷和绝缘子相关缺陷。
(2)4种缺陷类型下SO2F2的含量从大到小依次为N 类缺陷、G 类缺陷、P 类缺陷、M 类缺陷,其中N类缺陷下SO2F2含量远大于其他3种缺陷,因此可以将其作为辨别PD下N类缺陷的特征。
(3)对于两种含碳类组分,不同放电量下的M类缺陷和G 类缺陷的CO2和CF4含量都普遍高于N类缺陷和P 类缺陷,因此可以用这两种组分含量的占比作为判断故障是否涉及有机固体绝缘材料。其中CF4含量在不同类型缺陷下对比尤为明显,CF4含量大小关系为:0.02% 借鉴变压器油中溶解气体大卫三角形法的思想来构建适用于GIE 故障诊断方法,三角形的三条边分别代表3个不同特征量的占比,因此需要从已有的7 组组分特征量(CO2+CF4、CO2、SO2F2、SOF2、SO2、CF4和SO2+SOF2)中选择3 组能够较好地表征出不同故障的特征量进行下一步分析,使特征量与故障种类之间的相关性最大化。另外,为了使得三角形的三条边坐标轴两两之间尽量不存在关联关系,则需要选择的这3 组特征量彼此之间尽可能的相互独立,使特征量之间冗余性最小化。 为使提取的特征量更能独立有效地表征不同的故障类型,同时尽量减少人为主观因素对组分特征量提取过程的干预,本文使用mRMR 准则对已有的特征集合中的特征量进行优先级排序,为后文诊断方法的构建奠定基础。mRMR 准则由PENG H等[20]在互信息的理论基础之上提出,该准则通过挖掘特征参量之间的关联关系,可以获取与目标类别相关度最大的特征参量集合。最大相关原则要求所选的特征集与目标类别有最大的依赖性,根据最小冗余原则,要求选择出来的最优特征集各特征之间的相关性最小,定义分别为式(1)~(2)[21]。 式(1)~(2)中:S表示特征子集;|S|为特征量的个数;fi、fj分别为第i和j个特征;c为目标类别;本文使用MIC代替原本公式中的互信息作为信息相关性度量准则,MIC(fi,c)表示特征fi和类别c之间的最大信息系数,MIC(fi,fj)表示两个特征fi和fj之间的最大信息系数。 常用信息差(MID)和信息商(MIQ)原则作为mRMR 准则的特征选择原则,即要求特征和类别之间的相关性D与类别和类别之间的冗余性R的差值或商值最大,其定义式分别为式(3)~(4)[22-23]。 由于MID 和MIQ 很大可能会得到不一样的结果,为了更好地利用两个准则,本文还计算信息差和信息商的和作为一种附加的特征选择准则,即MID+MIQ,如式(5)所示。 mRMR 准则在实际应用中,首先将各组分特征量中与故障类别之间MIC值最大的特征组分作为筛选出的第一个特征量,接下来要逐一搜索出满足maxΦ1、maxΦ2或maxΦ3的特征量,通常采用增量搜索算法来选择。假定现已经计算得到了由m个最优的特征构成的特征集Sm,然后用公式(6)~(8)来搜索第(m+1)个特征。 基于mRMR 的MID、MIQ 和MID+MIQ 原则,将各组分含量经过归一化处理后的数据作为mRMR 的输入原始特征集合,使用如图2 所示的流程对SF6分解组分的含量进行特征排序,生成最优特征排序构成候选特征子集,最终得到的特征排序如表1所示。从表1中MID、MIQ和MID+MIQ三种原则下的特征排序进行分析,x′(CF4+CO2)和x′(SOF2+SO2)在3种特征选择原则上均是排名前两位的特征量,因此需要留下。考虑到x′(SOF2+SO2)中已涉及到SO2和CO2,在MIQ 和MID+MIQ 这两种原则下SO2F2的表现均优于CO2,因此可选择x′(SO2F2)作为第3个特征量。 图2 特征排序流程Fig.2 Flow chart of feature sorting 表1 特征排序结果Tab.1 Feature ranking results 上一节已筛选出用于表征GIE设备绝缘故障特征 的3 组特 征量{x′(CF4+CO2)、x′(SOF2+SO2)和x′(SO2F2)},将各特征组分含量的占比作为三角形的3条坐标轴构建一个等边三角形坐标系,三角形区域中每个点平行三边做平行线后与三个坐标轴的交点的数值满足和为100%。 使用%(CF4+CO2)、%(SO2F2)、%(SO2+SOF2)三组组分特征量构建适用于PD 4种缺陷类型的三角形故障诊断方法,本文称之为“PD-三角形故障诊断方法”。%(CF4+CO2)、%(SO2F2)、%(SO2+SOF2)分别表示各特征量在所有特征量中的占比。 根据局部放电分解组分含量随时间的变化规律,一般在36 h 后3 组特征量的比例逐渐趋于稳定[19],因此,使用局部放电36 h的分解组分含量作为初始数据,实验平台如图3 所示。输入数据得到三角形数据分布图形如图4 所示。从图4 可以看出,4类缺陷数据分布大致呈椭圆形,各类数据点之间区分不明显,需要改变三条边的特征量权重。 图3 局部放电实验平台图Fig.3 Platform for PD experiments 图4 原始三角形诊断分布图Fig.4 Original distribution of triangle diagnosis method 由于PD 缺陷下的训练数据较少,覆盖区域相对较小,难以使用基于数据分布密度的方法选择权重,这种情况需要寻找一种新的方法对特征量的权重进行赋值。高斯混合模型(Gaussian mixture mod‐el,GMM)[24]是一种目前广泛应用的聚类算法,本质上是多个高斯分布函数的线性组合。聚类中常用的K 均值聚类和模糊聚类对于类簇的形状均假设成近似圆形(球形),对其他形状类簇聚类的效果较差,而GMM 能够处理更多的分布情况,可以用来描述不同形状的类簇(如椭圆形),对于解决同一集合下多种不同分布的情况较为有效,且GMM 对异常值有着较好的可识别性。GMM 通常使用期望最大(expectation maximization,EM)算法进行参数估计。 对于图4,数据点普遍存在%(CF4+CO2)和%(SO2F2)较小的情况,尤其是%(SO2F2),除了金属突出物缺陷,其他3种缺陷类型数据的%(SO2F2)不超过20。因此需要对CF4+CO2和SO2F2这两个特征量进行赋权,设CF4+CO2的权重为i,SO2F2的权重为j,使用二维下GMM 算法计算i∈(1∶5)和j∈(1∶10)时的聚类准确率,选择能使准确率最大的i和j值作为两者的权重。三角形坐标平面任一点(Adata,Bdata)对应到二维坐标平面的坐标值为(Xdata,Ydata),如图5所示,对应关系为式(6)。 图5 两个坐标系对应示意图Fig.5 The corresponding diagram oftwo coordinate systems 将不同i,j值下的各故障数据点对应的二维数据坐标(Xdata,Ydata)进行GMM 聚类,各权重i,j值下的聚类准确率如表2所示。 表2 各权重下GMM聚类准确率Tab.2 GMM clustering accuracy rate under each weight 当i=1,j=4 时,聚类准确率最大,为95.8%,使用%(CF4+CO2)、%(4SO2F2)和%(SO2+SOF2)这三组组分特征量构建“PD 类型-三角形故障诊断方法”,绘制出的三角形诊断图形如图6所示。区域界线的确定仍按照线性分类准确性最大为标准,4 条区域边界线及对应的值在图中标出,此时仅有5 组自由金属微粒缺陷下故障数据误判,其余均得到正确的分类。造成自由金属微粒缺陷诊断准确率低的主要原因是:该绝缘缺陷PD 固有的分散性导致SF6分解特性存在极大的分散性。 图6 PD类型-三角形故障诊断方法Fig.6 PD type-triangle diagnosis method 为验证所建立的三角形故障诊断方法的准确性,本文使用文献[25]获取的PD 三种缺陷数据进行方法测试,测试样本共90组。根据CF4、CO2、SO2F2、SOF2和SO2这5种分解产物的浓度值分别计算出两个诊断方法所涉及的特征量,并在三角形故障诊断坐标系中绘制数据点,根据故障数据点所属的分布区域判断其所代表的故障类型。测试样本在三角形故障诊断图中的分布如图7 所示,测试样本数据分布及辨识情况如表3 所示。图7 中,90 组测试样本中89 组故障被正确辨识,综合辨识率达到98.9%,表明本文建立的PD 类型-三角形故障诊断方法具有较好的故障识别效果。 图7 PD类型-三角形故障诊断方法测试样本分布Fig.7 PD type-triangular fault diagnosis method test sample distribution 表3 测试样本数据分布及辨识情况Tab.3 Data distribution and identification of test samples 本文基于SF6局部放电分解特性,提取表征局部放电的主要特征组分,并借鉴大卫三角形法的思想,提取特征组分并基于高斯混合模型对初始三角形诊断方法进行改进,构建出适用于诊断SF6气体绝缘设备局部放电故障的新型方法——PD-三角形诊断方法,得到以下结论: (1)全面考量了SF6局部放电故障下的主要分解气体组分的化学稳定性、检测难度以及生成量,选择CF4、CO2、SO2F2、SOF2和SO2作为特征分解气体,用于特征量的构建。 (2)基于mRMR 的MID、MIQ 和MID+MIQ 原则,将特征含量经过归一化处理后的数据作为mRMR 的输入原始特征集合,对SF6分解组分的含量进行特征排序,获得最优特征排序。基于特征排序,选取%(CF4+CO2)、%(SO2F2)、%(SO2+SOF2)三组组分特征量构建的三角形故障诊断方法提升了故障类型的辨识效果,并且实现了对3种绝缘子缺陷的辨识。 (3)基于高斯混合算法,进一步调整了新三角形故障诊断方法的三组特征量的权重,对诊断方法进行了进一步改进。使用研究数据进行测试,结果表明改进的PD 类型-三角形故障诊断方法对PD 缺陷类型的综合辨识率高达98.9%,具有极高的应用价值。基于本文建立三角形诊断法的算法和思路,可通过编程制作软件用于现场故障诊断。仅需输入特征分解组分含量,即可获得故障点在三角形坐标系的位置,判断故障所属类型。1.2 基于mRMR准则提取分解组分特征


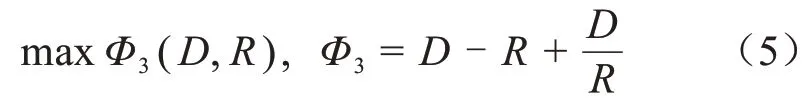
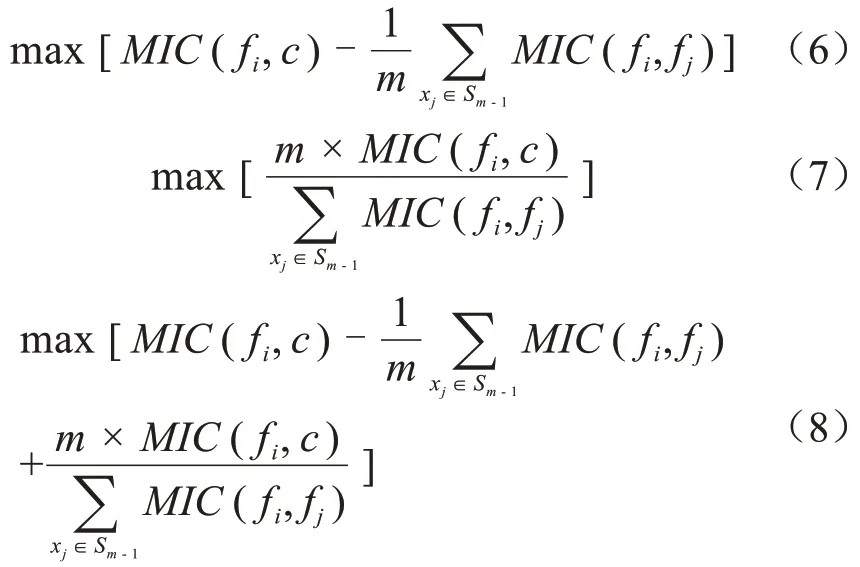

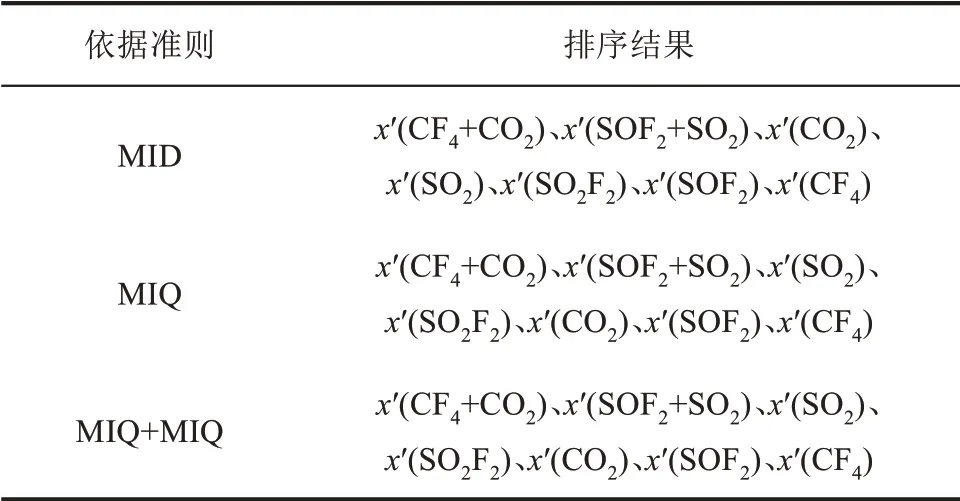
1.3 建立初始的三角形故障诊断方法


2 基于高斯混合模型改进PD 类型-三角形故障诊断方法




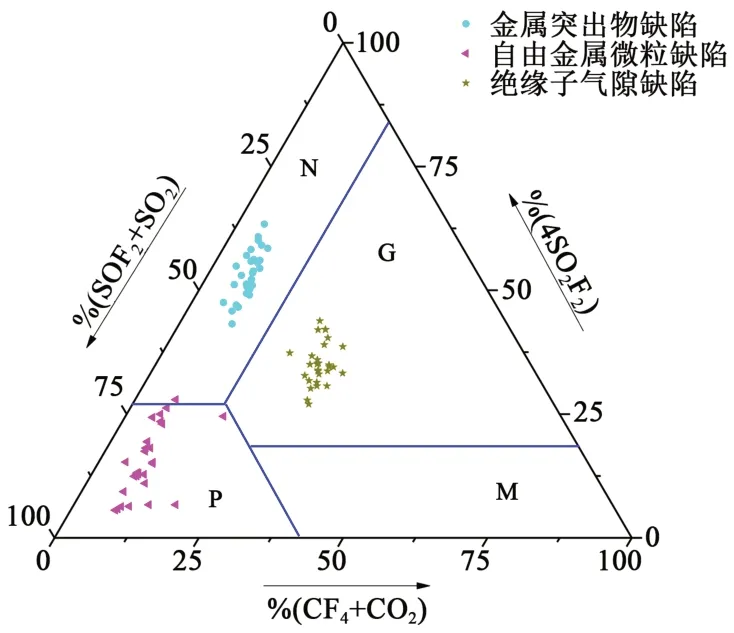
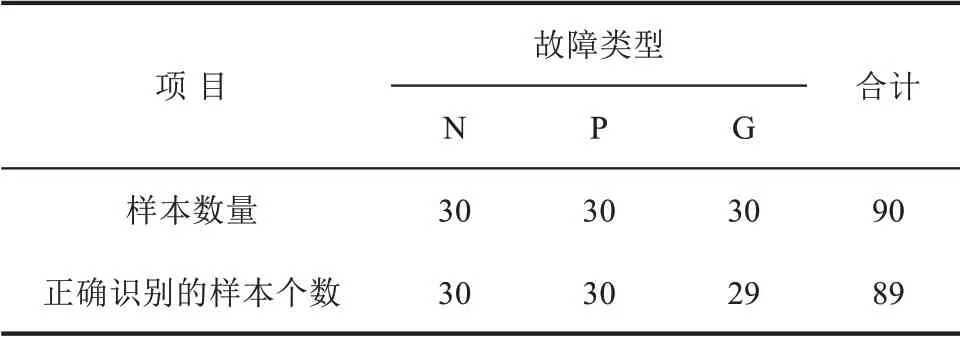
3 诊断方法测试
4 结论
